Rep:Mod:ap3714yr3ts

Introduction

Aims

In this project, computational methods are employed in order to model and characterise the transition states for two well-known types of pericyclic processes: a [4+2] cycloaddition (Diels-Alder reaction) and a [4+1] cycloaddition (Cheletropic reaction). From here, the favourable reaction pathways are aimed to be discussed based on an assessment of thermodynamic factors (e.g. enthalpy), kinetic factors (e.g. activation energy) and molecular orbital interactions.

Finding the transition states and minima on the PES

The software used is Gaussian 5.0, a tool which involves exploring the PES (potential energy surfaces) and allows setting up calculations in order to extract useful information from this PES. The PES is a mathematical function of the energy of a system versus a certain set of coordinates. Most often, the (x,y,z) position coordinates are used, hence, for a large molecule, there will be 3N coordinates (where N is the number of atoms). Since the mass motion centre is removed (3 rotational and 3 vibrational coordinates), there will be 3N-6 coordinates left, which are usually termed degrees of freedom. When the PES is plotted against only one coordinate (having only one degree of freedom), the resultant is called the energy profile.

For a certain process, Gaussian calculations can envisage the lowest energy pathway from a PES. In the context of a reaction, this is the IRC (intrinsic reaction coordinate) and is obtained by locating the minima corresponding to the reactants and the products and linking them through a path for which the total energy is also a minimum.

This is achieved by analysing the gradients and curvatures at points on PES, which gives information about critical points (minima, maxima and saddle points).

In a critical point, the gradient or first derivative of the potential energy with respect to any coordinate is 0.

$\frac{\partial E(x)}{\partial x}=0$, where x is an example of coordinate

In order to decide the exact nature of the critical point, the second derivative (curvature) needs to be evaluated in these points. In particular, for a minimum this second derivative would be greater than 0, as result of the fact that the point is situated at the base of a convex curvature. By contrast, a transition state is described by a saddle point, being a maximum along the reaction pathway, but a minimum with respect to other coordinates.

$\frac{{\partial }^{2}E(x)}{\partial x^2}>0$, where x is the reaction path confirms a minimum point

$\frac{{\partial }^{2}E(x)}{\partial x^2}<0$ indicates a maximum or a saddle point. The second partial derivative test can be used in identifying saddle points.

Since the second derivative is linked to the force constant in the Harmonic Oscillator equation, a negative value of it would be reflected in an imaginary frequency, meaning that a minimum on the PES has not been found.

$v=\frac{1}{2\pi }\sqrt{\frac{k}{\mu }}$

The calculations that follow have been done using first of all the PM6 semi-empirical method and then re-optimised with the higher basis set method, B3LYP. Links for the log files for the calculations can be found here.

Exercise 1 - Diels-Alder reaction of 1,3-butadiene with ethene

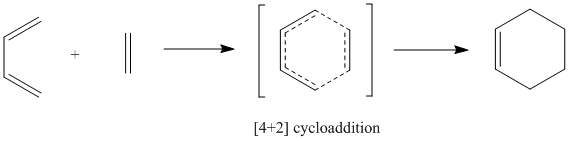
The image above depicts the Diels-alder reaction between 1,3-butadiene and ethene from the theoretical point of view, passing through a cyclic 6-electrons transition state to form the product, cyclohexene. The transition state was located with the aid of computational methods, animated and further characterised from the point of view of molecular orbitals interactions and bond lengths. First of all, the reactants energies were minimised using the PM6 optimisation method. In particular, for the case of butadiene, the s-cis configuration takes part in the reaction, hence this is the geometry that had to be minimised. Successful optimisation occurred when the two double bonds are slightly distorted form coplanarity as seen below, as this minimises potential repulsions.

Optimised s-cis Butadiene

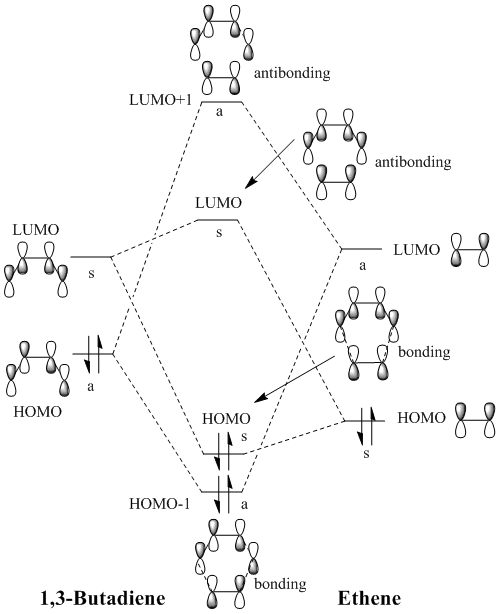
MO diagram and visualisation of MOs

Rules for orbital interactions

The figure above represents the butadiene/ethene TS formation from the MO point of view. The approximate energy ordering of the molecular orbitals drawn was estimated from the reactants and TS computation outcomes. As it can be seen, the Diels-Alder reaction is based on interactions between occupied and unoccupied molecular orbitals. Crucial for the success of the reaction: The molecular orbitals should be close enough in energy in order to interact - as seen in the frontier molecular orbitals diagram, the HOMO of the butadiene is closest in energy to the LUMO of the ethene, making their interaction strong and leading to a great stabilisation by the formation of the filled HOMO-1. On the other hand, the ethene HOMO could interact with the LUMO of the diene (this is met in the inverse electron demand Diels-Alder reaction), but in this case the energy splitting wouldn't be that high. Both type of interactions are seen to be occurring at the transition state, giving rise to 4 molecular orbitals which can be depicted in the figure on the right and are correlated to the ones from the MO diagram above. However, based on the relative energy heights of the 4 MO's, we can rationalise that this is a normal electron demand reaction, since the great energy splitting between HOMO-1 and LUMO+1 can only arise if the dienophile HOMO - diene LUMO interaction is favoured. The molecular orbitals should have the same symmetry - we can talk about a conservation of symmetry. For example, the symmetric LUMO of the butadiene interacts with the symmetric HOMO of the ethene, as the orbital overlap integral is non 0, giving rise to 2 new symmetric MO's (HOMO-1 and LUMO+1). The conclusion is summarised in the table below:

MOs for the Diels Alder reaction

Symmetry MO1	Symmetry MO2	Orbital overlap integral	Interaction allowed?
symmetric	symmetric	non 0	allowed
antisymmetric	symmetric	0	forbidden
symmetric	antisymmetric	0	forbidden
antisymmetric	antisymmetric	non 0	allowed

Bond lengths analysis

Bond lengths (Å) Carbon van der Waals radius (Å) Atom pair Ethene Butadiene TS Product Literature (cyclohexene) Typical sp3 C-C Typical sp2 C-C 1-4 - 1.33539 1.37977 1.50085 1.504 1.54 1.33 1.7 4-6 - 1.46834 1.41111 1.33697 1.335 6-8 - 1.33539 1.37975 1.50085 1.504 8-11 - - 2.11486 1.53715 1.550 11-14 1.32736 - 1.38175 1.53460 1.515 14-1 - - 2.11461 1.53715 1.550

Optimised reactants, at infinite separation:

• Butadiene - double bond lengths are in good agreement with the standard value (1.33 Å). the single C-C bond is a bit shorter than the typical value (1.47 compared to 1.54)
• Ethene - double bond lengths are in good agreement with the standard value (1.33 Å)

Transition state: As the reactants approach, the bond lengths and distances change as follows:

• Double bonds (1,4, 6-8 and 11-14) - slightly elongate, as result of loosing the sp² character. They have values in between a C-C single and a double bond (1.38).
• Distances between the reacting termini (8-11 and 14-1)- achieve a value of 2.11, which is smaller than the sum of 2 carbon van der Waals radii (2.14), but larger than a C-C single bond.
• Single bond (4-6) - originally a single bond, its length decreases to reflect the partial double-bond character acquired.

Product: The 4-6 bond now has a value characteristic for double bonds, whereas the other bonds have now values that are typical for single C-C bonds. 1-2 and 6-8, originating from butadiene have lengths that are slightly shorter than the sp³ C-C typical ones.

There is a good agreement with the literature data for the product bond lengths, as it can be seen in the table above.

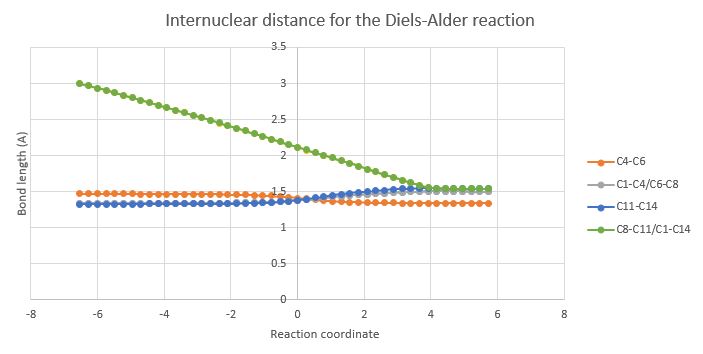
To summarize the findings, as we approach transition state, the bonds that originate from the reactants gain a partial double bond character. The whole phenomenon is depicted in the graph below. The green line represents the shortening of the distance between the two reacting termini, until a length of 1.54 Å is reached (value for the typical single bond). The rest of the bonds also increase towards 1.54 Å, except for C4-C6 which corresponds to the double bond in cyclohexene.

Vibrations at transition state and synchronicity of bond formation

The first two normal modes for the optimised transition state can be visualised on the left. The first coordinate corresponds to the imaginary frequency (in this case 948.78i) and it shows the reactive termini (2 atom pairs) being brought together in order to bond and become sp3 hybridised. On the other hand, the second coordinate is the first positive frequency (in this case 145i) and shows each individual molecule rotating/twisting around its own centre of symmetry. This helps alleviate the hindrance between the methylene groups, however it is not indicative of any bond forming process. As it can be seen in the animation, the bond formation is synchronous, as the two reacting termini approach each other concomitantly. This is supported by the graph showing the evolution of the bond lengths C1-14 C-8-11 (the two bonds evolve in the same way, at the same time, being overlapped on the plot in discussion).

Nf710 (talk) 00:38, 16 December 2016 (UTC) Very good first section. Nice use of the python script and excellent formatted. Good understanding of electron demand.

Exercise 2 - Endo and Exo Diels-Alder

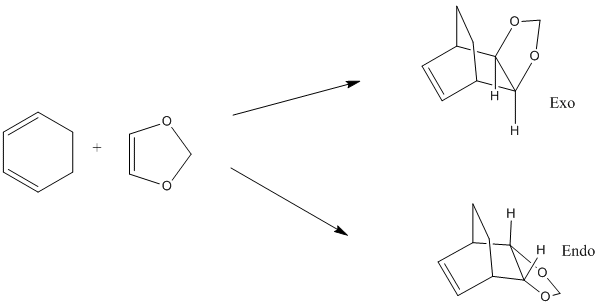
In this exercise, the Diels-Alder reaction between cyclohexadiene and oxolane is studied. The preference for the endo/exo isomer is explained with the aid of reaction energies and barriers and the orbital interactions in the transition state and the products are examined.

Electron demand of the Diels-Alder reaction

The electronic demand of a Diels-Alder reaction is explained based on the degree of overlap/interaction between the frontier molecular orbitals (HOMO and LUMO) of the reactants. Two orbitals that are close in energy can overlap strongly and this is reflected by a high energy splitting between the resulting bonding and antibonding MOs. Starting from the case of the Diels-Alder diagram in exercise 1, the relative energies of the HOMO and LUMO's for any of the reactants can be altered by the introduction of EWG (electron withdrawing groups) - or EDG (electron donating groups). This can affect the way in which these FMOs can interact and the possibilities are shown below, accompanied by a representation of the bonding MO resulting from each case:

MOs for the exo reaction (B3LYP)

MOs for the endo reaction (B3LYP)

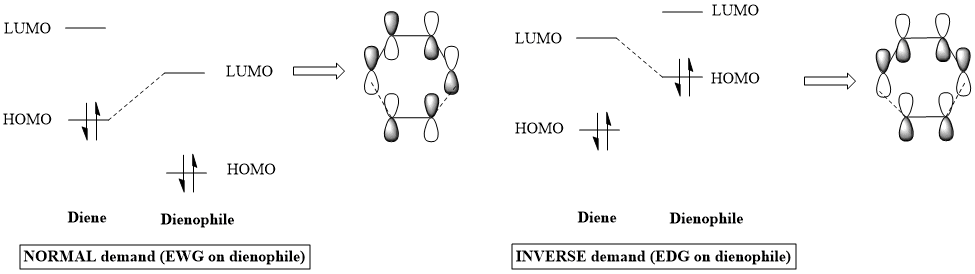
For this example, the MO diagram from Exercise 1 can be applied. It can be seen that the HOMO-1 and LUMO+1 are in both cases asymmetric, corresponding to a pair of bonding/antibonding MO's that are derived from the interaction of the HOMO of the diene with the LUMO of the dienophile. Also, HOMO and LUMO are symmetric in both cases, as they are derived from the interaction between the LUMO of the diene and the HOMO of the dienophile. We need to look at the degree to which the HOMO orbitals are stabilised in each case, as this would give us information about how close they are to their LUMO correspondent with which they interact. This can be done by substracting the energies of the bonding orbitals from the energies of the HOMO they come from. The bonding orbitals are HOMO-1 and HOMO. In both cases, the HOMO of the diene is the most stabilised, the difference between itself and the bonding orbital it forms being 20KJ/mol for exo and 24KJ/mol for endo. On the other hand, for the dienophile HOMO, the bonding orbitals derived from it are at energy differences of around 17KJ/mol (exo) and 4KJ/mol (endo) relative to this HOMO. (The contrast between endo and exo in the latter example may be caused by secondary orbital interactions in the endo configuration, which raise the energy of the diene LUMO, making its interaction with dienophile HOMO less favourable. The secondary orbital interactions are explained at the end of this exercise). To conclude, the FMO's that appear to interact the strongest are the HOMO of the diene with the LUMO of the dienophile, making this reaction a normal demand Diels-Alder.

(This is an interesting take on the problem. However, the MO energies that come out of Gaussian aren't entirely physical and I don't think it's possible to get anything out of subtracting energies between two different systems. Tam10 (talk) 12:02, 12 December 2016 (UTC))

Energy barriers and reaction energies analysis

NOTE: The conversion used was from an available online tool found [1] 1 Hartree/mol = 2600 KJ/mol

Approach Energies (KJ/mol) PM6 Ea ΔrGθ Hexadiene Oxolane Transition state Product Endo 308.57 -137.25 362.17 99.20 190.85 -71.12 Exo 308.57 -137.25 364.70 99.70 193.38 -71.62

Approach Energies (Hartree/mol) B3LYP Ea ΔrGθ Hexadiene Oxolane Transition state Product Hartree KJ/mol Hartree KJ/mol Endo -233.323720 -267.068132 -500.332149 -500.418691 0.059703 1.62 -0.026839 -70.47 Exo -233.323720 -267.068132 -500.329168 -500.417322 0.062684 1.65 -0.025470 -66.87

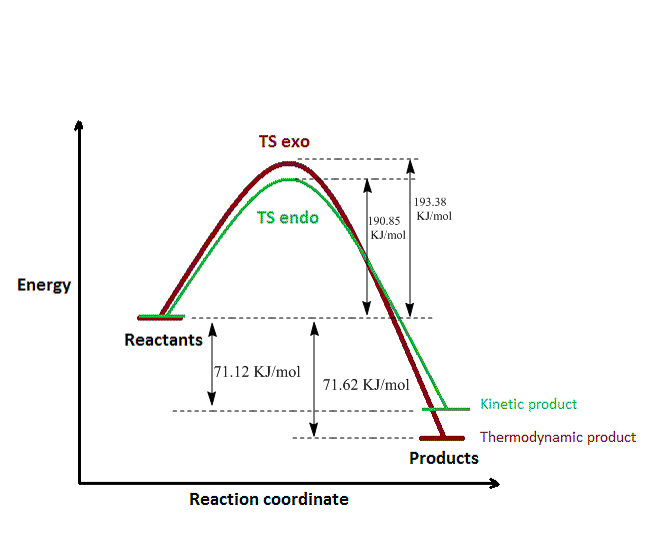
The data from the tables is summarised in the plot below. For the endo approach, the transtition state is lower in energy by almost 3 KJ/mol (in both B3LYP and PM6). This means that the energetic barrier for the reaction in this case is lower, hence it is more likely that it would be overcome at room temperature, leading to the formation of the endo adduct. The endo adduct is therefore the kinetic product, however, it can be seen that this is not the most stable one. From the thermodynamic point of view, the exo product is the most stable, as it has the lowest total energy, which is reflected in the ΔrGθ value (more negative ΔrGθ).

Nf710 (talk) 10:24, 20 December 2016 (UTC)This graph should have been done with the B3LYP energies as they are better.

Nf710 (talk) 10:27, 20 December 2016 (UTC) The endo is both you should have used the B3LYP values to tell you this.

Secondary orbital interactions

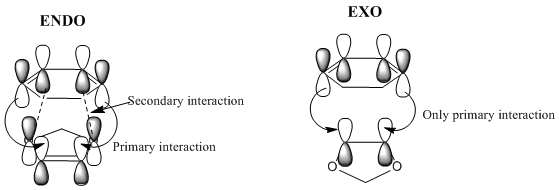
The preference for either adduct and the energy barriers can be explained in terms of stereoelectronics. In the endo transition state, the two p orbitals on the oxolane oxygens have the right orientation to interact with the diene pi orbitals, giving rise to a secondary interaction. Overall the bonding in this MO is enhanced. This leads to a stabilization of the transition state, which will be lower in energy in case of the endo adduct. However, in the case of the exo adduct, this additional stabilization can't occur, as the orbitals are now pointing away from each other and the interaction can no longer take place.

endo TS- HOMO orbital

exo TS - HOMO orbital

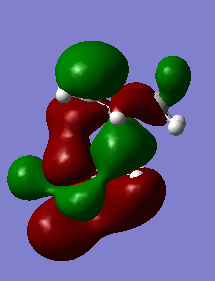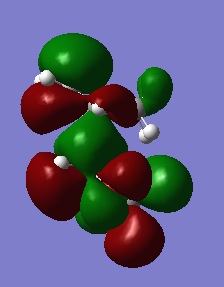Exercise 3

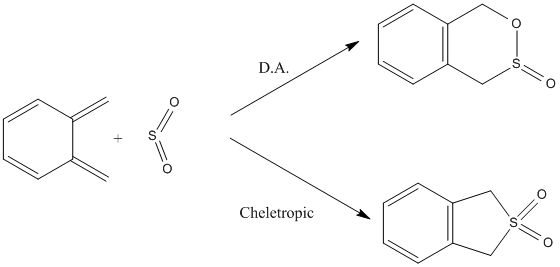
In this exercise, two different types of cycloadditions are studied starting from the same substrates (sulfur dioxide and xylylene). These can either undergo a [4+2] cycloaddition (Diels-Alder) or a [4+1] one (termed cheletropic reaction). The most favourable pathway will be predicted based on energetic considerations.

IRC for the Diels-Alder vs Chelotropic pathways

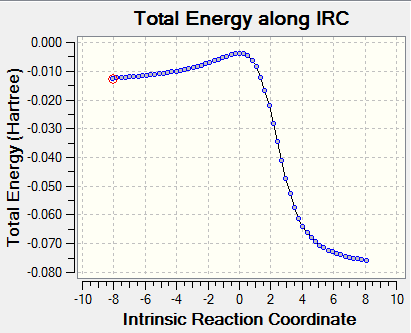
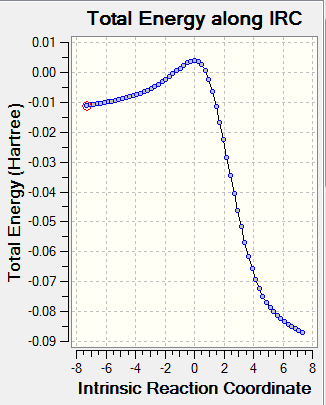
First of all, the endo and exo Diels-Alder products were optimised at the PM6 level. The reacting termini were then separated and fixed at a distance of 2.2-2.4 A and a transition state calculation was performed also at the semi-empirical level. One negative vibration confirmed a TS in each case: exo (333i), endo (351i). In case of the Cheletropic reaction, the negative frequency at TS was 485i.

Based on the TSs, the reaction pathways were animated with the aid of IRC (30 steps) calculations. These are represented in the table below and show a concerted reaction in each case.

EXO

ENDO

CHELOTROPIC

Exo	Endo	Cheletropic

(These IRCs look truncated. Not really a problem if the reactants/products are properly optimised Tam10 (talk) 12:02, 12 December 2016 (UTC))

As it can be seen in the table, according to Hammond's postulate, there is an early transition state in all cases, implying that the transition state will resemble the reactants best in terms of configuration and energy.

Energy barriers and reaction energies analysis

Type of adduct	Energies (Hartree/mol) PM6				Ea		ΔrGθ
	Sulfur dioxide	Xylylene	Transition state	Product	Hartree	KJ/mol	Hartree	KJ/mol
Endo	-0.118614	0.178035	0.090582	0.021455	0.031161	81.8132117	-0.038281	-100.5067732
Exo	-0.118614	0.178035	0.092076	0.021455	0.032655	85.735709	-0.037966	-99.67974059
Cheletropic	-0.118614	0.178035	0.099058	-0.000002	0.039637	104.066951	-0.594233	-1560.15886

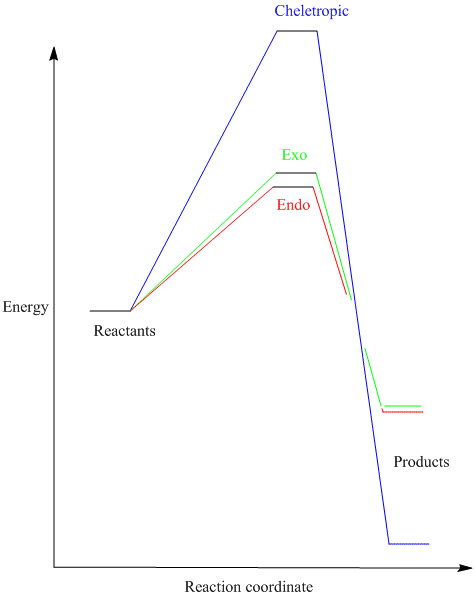
As in exercise 2, the activation energies and the Gibbs free energies were calculated in each of the three cases and the result summarised in an energy plot below.

The lowest activation energy was found, unsurprisingly, for the endo pathway of the Diels-Alder reaction. This can also be justified based on orbital interactions, as in exercise 2. The two pathways give rise to the same product, hence the similarity between their Gibbs free energies. In contrast, the chelotropic reaction has the highest energy barrier, requiring an extra energy of 20KJ/mol in order to reach the transition state, but there is now a very pronounced difference between the energy of the product and the energies of the reactants (Gibbs free energy).

From the thermodynamic point of view, the product of the chelotropic reaction is much more stable than the Diels-Alder ones (a 15-fold increase in the G difference), however, its formation is at the expense of passing a relatively high energy barrier. The unusually high stability seen here is supposed to be given by the sulfolene unit (5-membered ring containing sulfur).

However, the energy differences predicted here are much higher than the ones found in literature, where the activation energy for the cheletropic reaction is just 35KJ/mol and the G difference between products and reactants is just 40KJ/mol.

Xylylene at the TS

The xylylene starting material is particularly unstable, as the exo double bonds are not compatible with preserving aromaticity in the 6-membered ring. Hence, we can see in the transition structures (IRCs above) that the exo double bonds disappear in the favour of creating aromaticity within the benzene ring (the bonds in the 6-membered ring all become intermediate between single and double), since this phenomenon provides thermodynamic stability. Once the aromaticity is gained, the reaction proceeds fast towards the formation of products and this is reflected by the steep slope between the transition state and the products in the IRC energy profiles. Xylylene itself is very unstable and can form a dimer or can undergo a [2+2] electrocyclic reaction to help re-gain aromaticity of the benzenoid ring.

(Very neat report! Tam10 (talk) 12:02, 12 December 2016 (UTC))

Conclusion

In conclusion, pericyclic processes were modelled with the aid of computational methods. Data analysis allowed identifying the thermodynamically versus kinetically favoured products in the case of a Diels-Alder reaction ([4+2] cycloaddition, exercise 2) and of a hetero-Diels-Alder reaction in competition with a cheletropic reaction ([4+1] cycloaddition).

However, the energy differences in the former case were not conclusive, even when calculated with both the semi-empirical method and with the more powerful one, DFT. The very small energy differences in that case put the result in doubt. Chemical intuition and the secondary orbital interactions tip the balance towards the fact that endo is indeed the kinetic product.

Also, the nature of the electronic demand in a Diels-Alder reaction was quite hard to see, even at the B3LYP level, as all the possible interactions between the reactant frontier molecular orbitals can be seen. On the other hand, the methods employed does no fail to provide a good animation of the reaction path and a representation of the transition state vibrations that lead to product formation. Moreover, the bond lengths studied were also in good agreement with the literature.

Log files

Exercise 1

• Optimised reactants PM6: Media:ETHENE_SOFIA.LOG Butadiene Jmol above
• Optimised TS PM6 - Jmol with vibrations above
• Product PM6: Media:PRODUCT_CYCLOHEXENE_SOFIA.LOG
• IRC 200 steps: Media:IRC_20STEPS_SOFIA.LOG

Exercise 2

• Optimised TS: LOADED ABOVE IN THE MO SECTION
• Optimised products: prod endo B3LYP | prod exo B3LYP
• IRC calculations: Media:EXO_IRC_10.LOG | Media:ENDO_IRC_10.LOG

Exercise 3

• Optimised TS: Media:TS_ENDO_OPTIM_PM6_SOFIA.LOG | Media:DA_TS_MINIMUM_PM6_SOFIA.LOG | Media:TS_CHELO_SOFIA.LOG
• Optimised products: Media:DA_TS_MINIMUM_PM6_SOFIA.LOG | Media:DA_EXO_OPT2_SOFIA.LOG | Media:PROD_CHELO_OPT_PM6.LOG
• IRC calculations: INCLUDED ABOVE