Transition States and Reactivity Computational Lab

Introduction

Potential Energy Surfaces

A PES (potential energy surface) is used to map out the relationship between the a reaction's geometry and it's potential energy. For a molecule with more than two atoms, a PES generally has a dimensionality of 3N-6, where N is the number of atoms. A PES is usually found for multiple reaction coordinates. However, when minimising about every degree of freedom and varying only one reaction coordinate, an energy profile can be obtained. For a typical energy profile, the reactants and products are minima, whilst the TS (transition state) is a maxima which needs to be passed to travel between the two. Since all but one degrees of freedom are being minimised, this suggests the TS connects the reactants/products as a maximum on the lowest-energy path between the two. Transferring this back to a PES, a minimum point is one where a small fluctuation in any direction will result in a raising of energy whilst the TS is a saddle point on a minimum energy path.

Both a minimum and a TS are stationary points and therefore will have first derivatives of 0 with respect to all degrees of freedom. The surface around a minimum must have positive curvature in all directions and hence the second derivative with respect to all degrees of freedom must be positive at a minimum. With a TS, however, it is a saddle point and therefore it must have negative curvature with respect to one degree of freedom but positive curvature with respect to all others. Therefore, a saddle point will have a single negative second derivative and positive second derivatives for all other degrees of freedom. A Hessian matrix describes the local curvature of a function of many variables, and hence the second derivatives mentioned could be found via inspection of the eigenvalues of a Hessian matrix.

The single point of negative curvature for the TS results in a negative force constant when calculating vibrational frequency modes of the molecules. Since the square root of a negative number is imaginary, every TS has a single imaginary vibrational frequency. This is an important point, and is used for the calculations in this report to help confirm the existence of a TS.

Nf710 (talk) 23:26, 8 February 2018 (UTC) Thisn is a welll explained section well done. You could have made it abit clearer with a diagram. But good understanding of the need to diagonalise the Hessian Matrix.

Computational Methods

Two approaches were used in this experiment to try and locate the TSː

1. A guess was taken as to how the TS would look. The reactants were then positioned together in such a way that reflected this guess, and the bond lengths adjusted to try and reflect the formation of certain bonds. The structure was then optimised to a TS. If the guess was good enough, the TS would successfully optimise and an IRC (intrinsic reaction coordinate) calculation could be run. Checking that the TS had successfully formed was done by checking for a single negative vibration in which the atoms forming/breaking bonds were moving towards/away from each other and by checking that the result had converged.

2. Either the product or the reactants were fully made (usually whichever consisted of fewer molecules) and optimised. The bonds and angles which changed throughout the reaction were then identified and the structure edited to reflect this change. The atoms directly involved in the reaction were then frozen and the rest of the structure optimised around them. They were then unfrozen and the TS calculation performed. This method proved far more reliable and was used for all exercises except for the first one.

Two computational methods were used when running calculations via GaussViewː the PM6 method (a semi-empirical method) and the B3LYP method (a DFT - density functional theory - method). Both methods utilise the Hartree-Fock method, a which uses a set of one electron wavefunctions to approximate the motion of electrons in a field of atomic nuclei^[1]. The PM6 method, being semi-empirical, uses a lot of approximations and empirically determined parameters with this method when solving the Hartree-Fock equations. Therefore, it runs more quickly but gives a less accurate result than the result given by the B3LYP method.

Nf710 (talk) 23:42, 8 February 2018 (UTC) B3LYP definately has a 2 electron part, this is where the exchange correlation part comes in.

The B3LYP method uses a hybrid method of Hartree-Fock and DFT by combining them and using one where the other falls short; Hartree-Fock, being a quantum mechanical method, is a good method for finding exchange correlation but can't reliably recover dynamic electron correlation. DFT, meanwhile, is not a quantum method and so can't find exchange correlation but has an exact form for dynamic electron correlation. B3LYP combines the two methods to get more accurate results than PM6. However, the use of more methodology results in a longer calculation time.

Nf710 (talk) 23:42, 8 February 2018 (UTC) Really good understanding here. You could havve really complimented it with some equations.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Very good section overall. Good job!)

Method 1 as mentioned in the introduction was used for this exercise at the PM6 level. From the transition state, an IRC was performed, which confirmed that the transition state had been correct. The product was taken from the IRC and also optimised to the PM6 level. In this section, the MOs of the reactants and the transition state are analysed and correlated to those seen in the MO diagram for the formation of the transition state. How the carbon-carbon bond lengths alter throughout the course of the reaction is also discussed.

Reaction Scheme

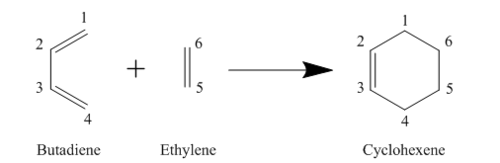
MO Diagram

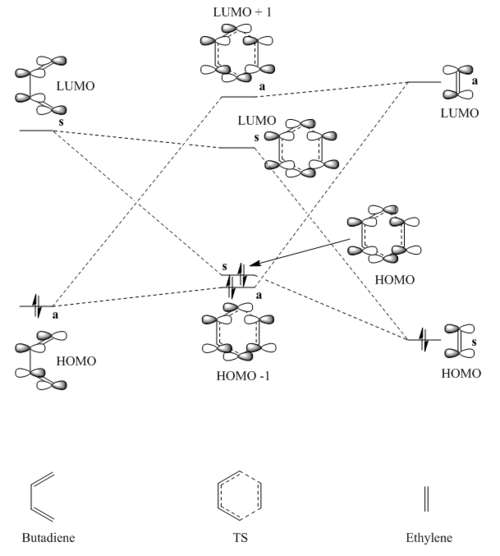
The MO diagram in figure 2 shows which orbitals on the reactants interact together to form the transition state orbitals. This occurs via interaction of the HOMO and LUMO (the frontier orbitals) on both reactants. These molecular orbitals are visualised via JMols below, with the four transition state orbitals being those formed from these interactions. As seen in the diagram, the butadiene HOMO mixes with the ehtylene LUMO to form one bonding (HOMO - 1) and one antibonding (LUMO + 1) orbital. These reactant orbitals are both antisymmetric, and hence so are both of those formed for the transition state. The symmetric orbitals, the ethylene HOMO and butadiene LUMO, also form one bonding (HOMO) and one anitbonding (LUMO) orbital, both of which are symmetric. From these observations it can be concluded that only orbitals of the same symmetries can react together. This is due to the orbital overlap integral, which measures the overlap of orbitals in space and is mathematically given byː

 $S_{P_{A}, P_{B}} = \int d V Ψ_{A} Ψ_{B}$   ^[2]

Where $Ψ_{A}$ and $Ψ_{B}$ are the orbitals for molecules A and B respectively. Orbitals of different symmetries (no net overlap) cannot interact due to constructive and destructive interference between them cancelling to zero. However, orbitals with the same symmetries (either both antisymmetric or both symmetric), can interact due to having net overlap which is either constructive or destructive overall. As such, an orbital overlap integral of zero would be obtained for an antisymmetric-symmetric pairing, whilst a non-zero integral would be obtained for an antisymmetric-antisymmetric or symmetric-symmetric pairing.

Because the diene HOMO-dienophile LUMO gap is smaller than the diene LUMO-dienophile HOMO gap, the reaction follows normal electron demand for a Diels-Alder reaction.

Reactant and TS MOs

Butadiene HOMO

Butadiene LUMO

Ethylene HOMO

Ethylene LUMO

TS HOMO - 1

TS HOMO

TS LUMO

TS LUMO + 1

Carbon-Carbon Bond Length Variation


Carbons	Reactants Bond Length / Angstrom	TS Bond Length / Angstrom	Products Bond Length / Angstrom
C1-C2	1.3334	1.3798	1.5009
C2-C3	1.4706	1.4111	1.3370
C3-C4	1.3334	1.3798	1.5008
C4-C5	N/A	2.1143	1.5372
C5-C6	1.3273	1.3818	1.5346
C6-C1	N/A	2.1151	1.5372

A typical sp³ C-C bond length is 1.543 Angstrom, whilst an sp² C=C bond length is 1.337 Angstrom. ^[3] These lengths are very similar to those for the single and double bonds seen in table 1, which shows the variation in C-C bond length throughout the reaction. The C1-C2, C3-C4 and C5-C6 sp² C-C bonds begin near the 1.34 Angstrom expected but lengthen over the course of the reaction and end near the 1.54 Angstrom typical of a single bond. This is to be expected, since the sp² C=C double bonds become sp³ single bonds. The transition state lengths for these bonds are therefore in between those values, as the bonds are lengthening as they become weaker. The C2-C3 double bond, on the other hand, strengthens and shortens over the course of the reaction as it becomes a double bond, reflected by its final length of 1.337 Angstrom. The Van der Waals radius of a C atom is 1.70 Angstrom ^[4]. The distances between C4-C5 and C6-C1 (the newly formed bonds) are approximately 2.115 Angstrom in the transition state, which is lower than twice the Van der Waals radius of a carbon atom but higher than that of a C-C single bond, which suggests that the bond between those carbons has begun forming at the transition state.

Confirmation of TS

By pressing the 'Toggle vibrate' below, the negative vibration corresponding to the transition state can be seen. It is typically recognisable by the atoms which have bonds forming between them moving together in the vibration. This vibration is a negative, imaginary vibration, of which there was only one present in the transition state. The formation of the two bonds can be seen to be synchronous from the vibration due to both sets of atoms for the newly formed bonds moving together at the same time.

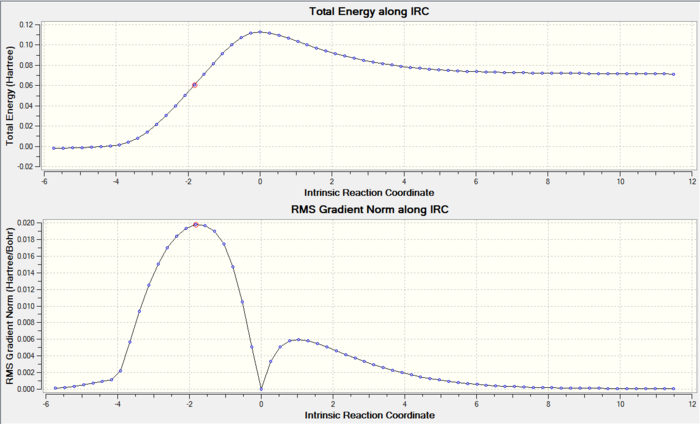
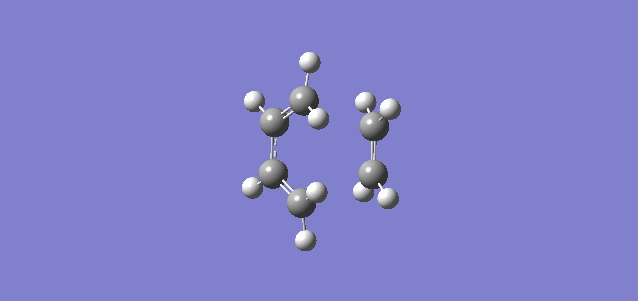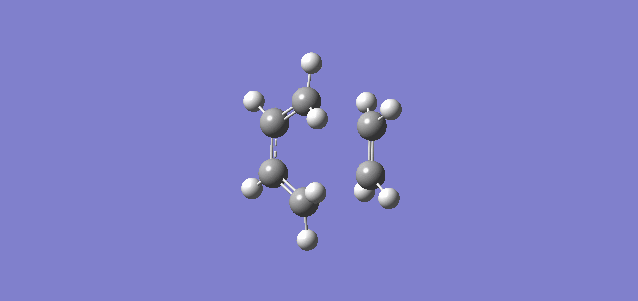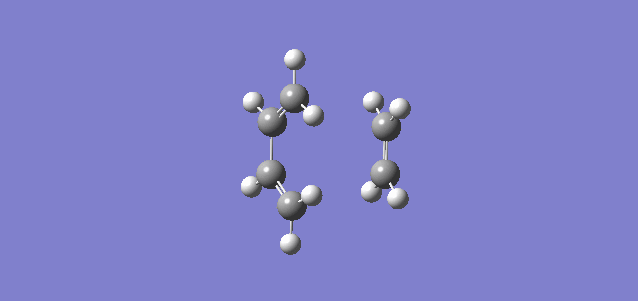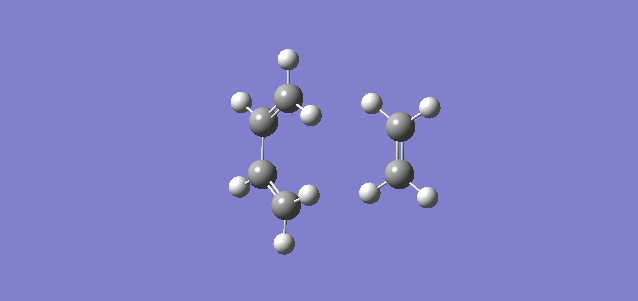
Figure 4ː Animated reaction. Animation plays once loaded.

The IRC path in figure 3 confirms that the TS was found correctly, whilst the animation in figure 4 shows the molecules rearranging as the reaction takes place.

Log Files

Log files for reactants, transition state and productː

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

This exercise was performed differently to exercise 1; it was performed vi method 2 as described in the introduction and optimised to a B3LYP level for a 6-31G(d) basis set. This allowed the transition state to be found, from which an IRC was once again run. This procedure was followed for both the exo and endo products. In this section, the MO diagram of the reaction is shown and discussed, as well as the energetic barriers present in the reaction. From energy comparison of the reactants and transition state, this reaction was found to follow inverse electron demand, unlike the reaction in exercise 1. This aspect is discussed below.

Reaction Scheme

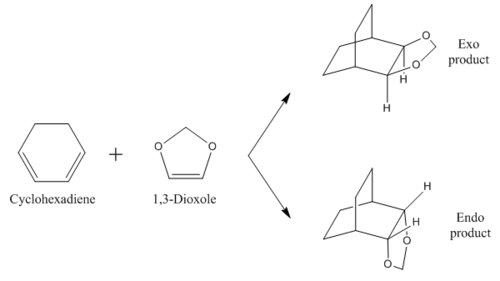
MO Diagram

(Fv611 (talk) Good MO diagram, but you do not discuss at all the difference between the exo and endo transition state in terms of relative energies of their respective MOs)

As previously, the JMols in the section below give a 3D representation of the frontier orbitals involved in this reaction for the reactants and products. Whilst the reaction in exercise 1 was a Diels-Alder which followed normal electron demand (the diene HOMO-dienophile LUMO gap is smaller than the diene LUMO-dienophile HOMO gap), this reaction follows inverse electron demand, in which the diene LUMO-dienophile HOMO gap is smaller than the diene HOMO-dienophile LUMO gap. The reason this occurs for this reaction whilst it did not for exercise 1 is the oxygen atoms present in the 1,3-Dioxole. These are electron donating, and hence can donate into the double bond, which raises the energy of both the HOMO and the LUMO for the dienophile component. This results in inverse demand, and explains why the reaction proceeds as it does.

Nf710 (talk) 23:44, 8 February 2018 (UTC) You could have shown this quanitatively if you had done a single point energy on the reactants of the IRC and looks at the ordering of the MOS when they are on the same potential energy suface.

Reactant and TS MOs

Cyclohexadiene HOMO

Cyclohexadiene LUMO

1,3-Dioxole HOMO

1,3-Dioxole LUMO

Exo TS HOMO-1

Exo TS HOMO

Exo TS LUMO

Exo TS LUMO+1

Endo TS HOMO-1

Endo TS HOMO

Endo TS LUMO

Endo TS LUMO+1

Energy Calculations

In the log files of the B3LYP optimised reactants, transition states and products, the Thermochemistry section was found. This contained a Gibbs Free Energy value, labelled Sum of Electronic and Thermal Free Energies. These values, given in hartrees, were collected and are shown in table 2 below.


Molecule	Gibbs Free Energy / E_h
Cyclohexadiene	-233.324
1,3-Dioxole	-267.068
Exo TS	-500.329
Endo TS	-500.332
Exo Product	-500.417
Endo Product	-500.419

The values of the product were summed and subtracted from the TS and product energies to find the reaction barriers and reaction energies for both reactions respectively. These values are shown in table 3. The hartree amounts were converted to kJ mol^-1 by dividing through by 3.8088 x 10^-4.


Measure	Exo	Endo
Reaction Barrier / kJ mol^-1	166.310	158.470
Overall Reaction Energy / kJ mol^-1	-65.152	-68.746

By looking at these values, it is clear that the endo product is both kinetically and thermodynamically more favourable. This is for different reasons; its thermodynamic favourability (lower overall reaction energy) has a steric cause. The exo product has a steric clash between the two bridging carbons and the exo oxygens, with both pointing up. This makes the exo product less stable, hence the endo product is preferred thermodynamically. Meanwhile, the endo product's kinetic favourability (which can be seen by its lower reaction barrier - 158.470 kJ mol^-1 compared to 166.310 kJ mol^-1 for exo) stems from a favourable secondary orbital interaction present in the endo TS. This interaction is shown in figure 7 and is between the p-orbitals on the oxygens and the diene $π$ system.

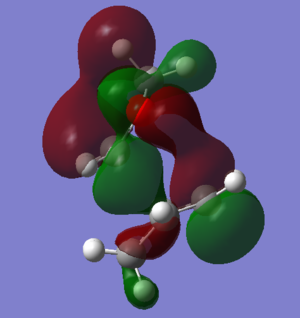
Nf710 (talk) 23:46, 8 February 2018 (UTC) Your energies are correct and you have come to the correct conclusions. Your discussion could have been complemented with some diagrams.

Log Files

Log files for reactants, transition states and productsː

Cyclohexadiene

1,3-Dioxole

Exo Transition State

Endo Transition State

Exo Product

Endo Product

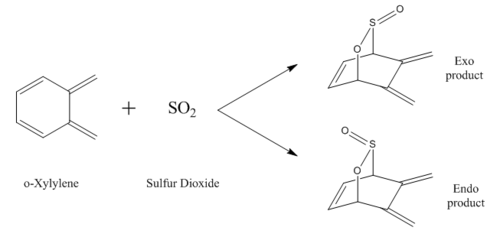
Exercise 3: Diels-Alder vs Cheletropic

This exercise was performed with the same methodology as exercise 2, using method 2. This reaction not only had an endo and exo pathway, but also another reaction type called a cheletropic reaction, which formed a new five-membered hetero ring. Also, due to o-Xylylene having two cis-butadiene fragments, there were also endo and exo pathways at the endocyclic site, inside the ring. The five different routes are analysed and compared below by finding IRCs and plotting their reaction energy profiles.

Reaction at Exocyclic cis-Butadiene Site

Reaction Scheme

IRCs

The IRC animations in figures 9 to 11 above show the interaction between the reactants in the formation of the products. By watching them, it is clear that the exo and endo Diels-Alder reactions involve asynchronous bond formation, with the two bonds forming at different times; since C-S and C-O bonds are of different lengths, the sulfur approaches the o-Xylylene with the oxygen closer to the carbon it is bonding to, which can explain this asynchronousness. The cheletropic reaction, however, undergoes synchronous bond formation, with the two C-S bonds forming simultaneously. A major driving force for all three reactions is the aromatisation of the six-membered ring in o-Xylylene. This drive to form the aromatic ring explains why o-Xylylene is highly unstable. The IRCs show that the aromatisation happens early in the reaction coordinate.

("Asynchronicity" is the word! Tam10 (talk) 13:42, 4 February 2018 (UTC))

Energy Calculations


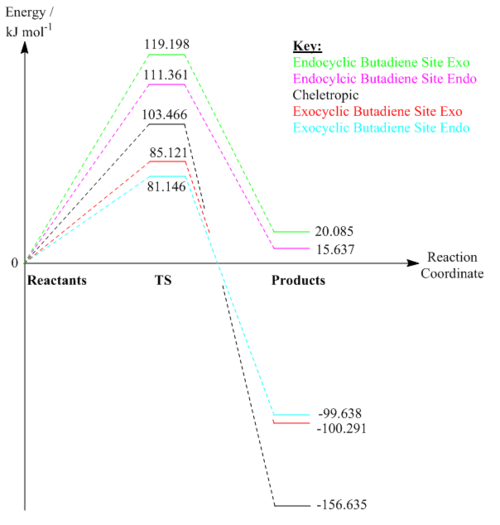
Reaction	Reaction Barrier / kJ mol^-1	Overall Reaction Energy / kJ mol^-1
Exo	85.121	-100.291
Endo	81.146	-99.638
Cheletropic	103.466	-156.635

Using the same methodology as for exercise 2, the reaction barriers and energies were found for the three pathways at the exocyclic butadiene site; they are shown in table 4. The energy profile in figure 12 below shows this pictorially. Of the three pathways, the endo Diels-Alder path is kinetically favourable, due to having the lowest reaction barrier (activation energy). This is due to the unbound oxygen atom, which can stabilise the transition state in the endo case via a secondary orbital interaction between the oxygen's p orbital and the $π$ system on the six-membered ring. This stabilising interaction is not present to the same effect for the exo Diels-Alder case. The cheletropic path has the highest activation energy due to the formation of a five-membered ring being far less favourable than the formation of a six-membered ring, due to the five-membered ring having ring strain. However, the cheletropic product is the thermodynamic product, since it still has both strong S=O bonds. These are energetically favourable, hence the product is the most stable. The exo product is more stable than the endo product due to the equatorial position the singly-bound oxygen occupies being more favourable than the axial position occupied by the same oxygen in the endo product.

Energy Reaction Profile

Log Files

Log files for reactants, transition states and productsː

Sulfur Dioxide

o-Xylylene

Exo Transition State

Endo Transition State

Cheletropic Transition State

Exo Product

Endo Product

Cheletropic Product

Reaction at Endocyclic cis-Butadiene Site

Reaction Scheme

IRCs

Figure 14ː IRC for exo Diels-Alder product formation. Animation should loop once loaded fully.

Figure 15ː IRC for endo Diels-Alder product formation. Animation should loop once loaded fully.

The IRCs above show that, just as for the exo and endo pathways at the other site, the reactions occur asynchronously. However, unlike the other reactions, at this site there is no point of aromatisation for the six-membered ring. This is mentioned below when discussing the energetics of these pathways.

Energy Calculations


Reaction	Reaction Barrier / kJ mol^-1	Overall Reaction Energy / kJ mol^-1
Exo	119.198	20.085
Endo	111.361	15.637

Shown above in table 5 are the reaction barriers and energies for the exo and endo Diels-Alder pathways at the enodcylcic cis-butadiene site. As can be seen, both reactions are endothermic overall, requiring an input of energy to proceed. When comparing these reactions to those at the other site in the energy profile in figure 12, it can be seen that both pathways are both kinetically and thermodynamically highly unfavourable. The reason for this is that the formation of the six-membered aromatic ring, which was one of the major driving forces in the other reactions, does not occur in these reactions. As well as this, they are kinetically unfavourable due to the ring strain they cause. The endo product is the more favourable of the two due to the destabilising steric clash between the oxygen and the ethyl groups on the exo product.

Log Files

Log files for transition states and productsː

Exo Transition State

Endo Transition State

Exo Product

Endo Product

Extension: Ring Opening of Aziridine

This extension was also completed using method 2 from the introduction. It was much harder to complete and required multiple attempts and inventive bond freezing to obtain the TS. Once obtained, the IRC clearly shows conrotation of the methyl groups present. This is discussed below.

Reaction Scheme

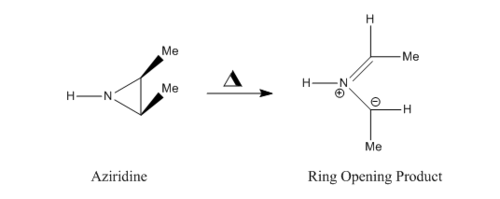
IRC

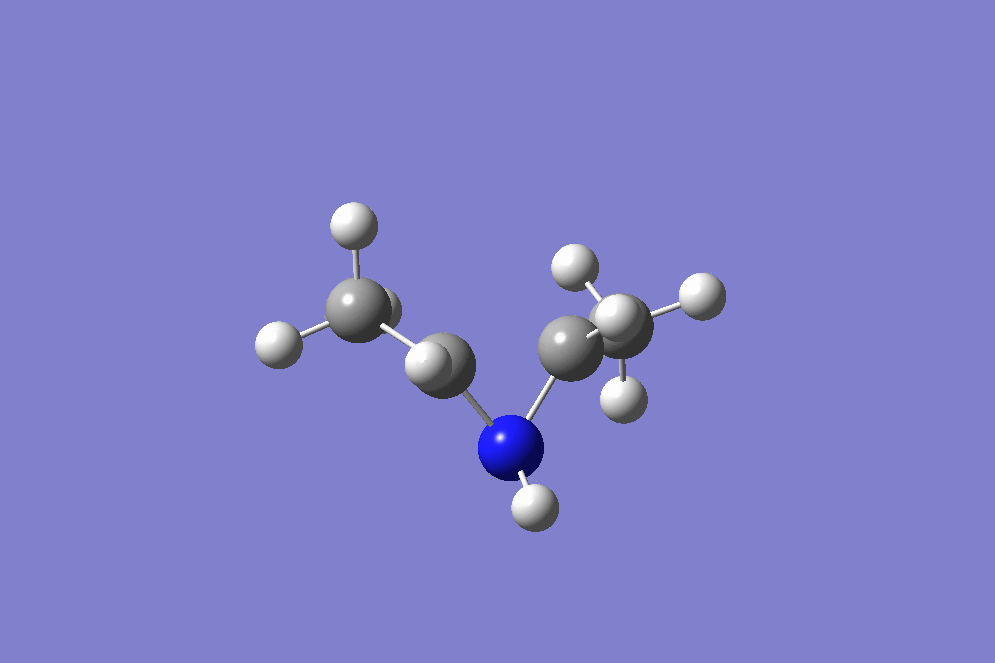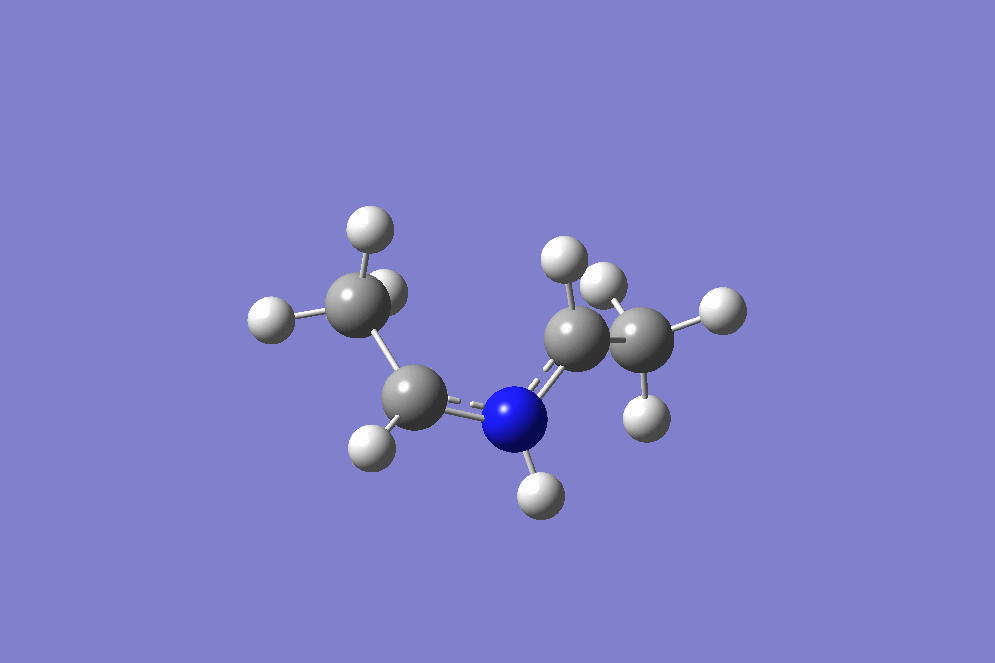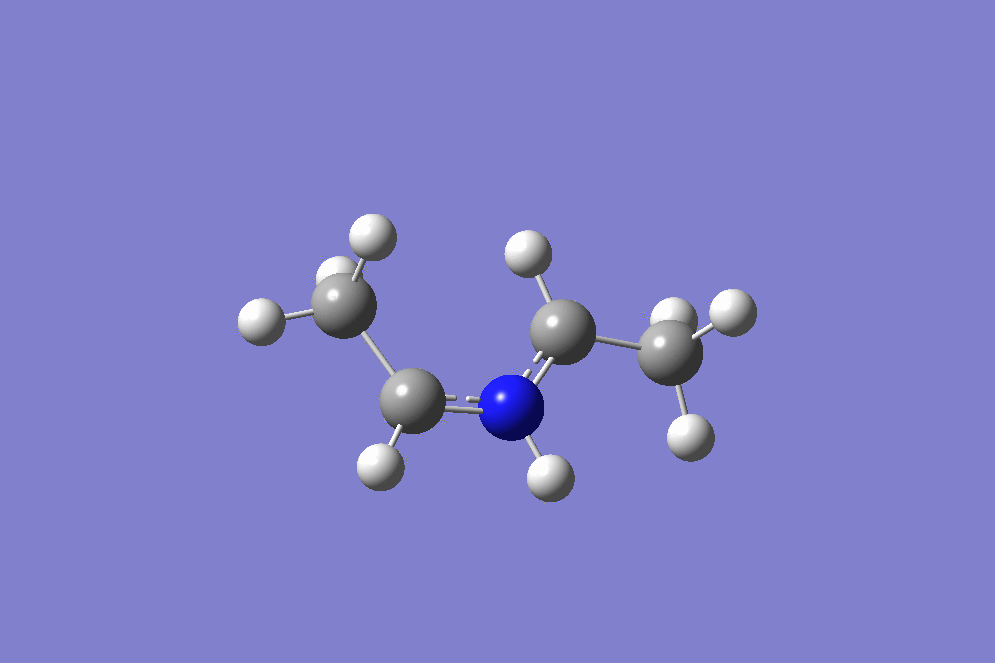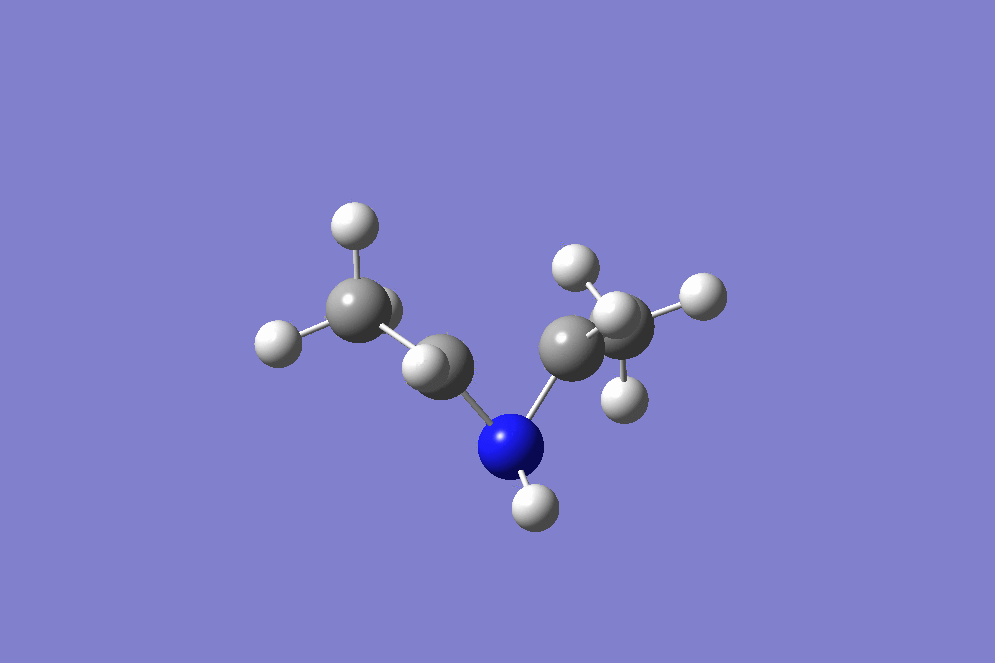
Figure 17ː IRC for ring opening of aziridine.

(Very good: the conrotation is clear Tam10 (talk) 13:53, 4 February 2018 (UTC))

MOs

Aziridine HOMO

Aziridine LUMO

TS HOMO

TS LUMO

Product HOMO

Product LUMO

Energy Calculations

Performing energy calculations for this reaction found the reaction barrier to be 148.524 kJ mol^-1, and the overall reaction energy to be -6.375 kJ mol^-1. This reaction barrier is high, which can be explained by the fact that a lot of energy is required to break open a ring. The energy of the product is only slightly lower than that of the reactant, hence it is possible that the two could interchange and be in equilibrium.

Analysis

The reaction is a 4 electron process, and is conrotatory under thermal conditions. Due to this, the two methyl groups rotate in the same direction at the beginning of the reaction, which can be seen at the the beginning of the IRC in figure 17. Figure 18 below shows the direction of rotation. The transition state for this molecule has a rare type of aromaticity called Mobius aromaticity. Unlike for compounds with the aromatic character of Huckel systems, the MOs in a Mobius armomatic compound have an odd number of out of phase overlaps. Therefore, in these case, 4n electron systems have an aromatic arrangement. Therefore, a transition state with 4 electrons, as with the one in question, can possess Mobius aromaticity ^[5].

(Looking at the HOMOs of the products and reactants, it's clear to see why a conrotation is needed. If you work backwards, the pi radical orbitals of the carbon atoms must rotate to form a bonding sigma interaction Tam10 (talk) 13:53, 4 February 2018 (UTC))

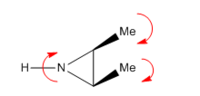
(Nice additional section. What would happen on the excited state, where electrons are populating the current LUMO? Perhaps worth describing what's going on with a drawing of the AOs Tam10 (talk) 13:53, 4 February 2018 (UTC))

(+8%)

Log Files

Log files for reactants, transition states and productsː

Aziridine

Transition State

Product

Conclusion

The practical was performed on three exercises and an extension exercise using the PM6 and B3LYP computational methods in GaussView. It was shown that these methods could be used to locate the transitions states of even relatively complex reactions, such as a pericyclic ring opening reaction, in a reasonable amount of time. As expected, the PM6 level performed quicker but optimised structures to a lower accuracy.

Exercise 1 was the simplest and so was completed via the method of guessing the transition state. This method yielded successfully optimised structures and was used to analyse the reaction, including the finding of the frontier orbitals involved. The Diels-Alder reaction was found to follow normal electron demand.

Exercise 2 was completed using the more complex method and the Diels-Alder reaction was found to follow inverse electron demand. The reactants, transition state and products were energetically analysed and it was found that the endo product was both the kinetic and the thermodynamic product. This was due to a stabilising secondary orbital interaction in the transition state and a less hindered steric arrangement respectively.

The more complex method was also used for method three. Reactions at the exocyclic cis-butadiene site found the endo product to be the kinetic one due to a stabilising secondary orbital interaction and the cheletropic product to be the thermodynamic one due to the energetic stability provided by two strong S=O bonds. Reactions at the endocyclic cis-butadiene site were found to be both kinetically and thermodynamically highly unfavourable.

An extension exercise looking at the ring opening of aziridine required multiple attempts to achieve the transition state. The reaction was found to be thermally conrotatory and underwent a Mobius aromatic transition state. It was difficult to assess the orbitals in order to explain any Woodward-Hoffmann analysis as to the reason it was conrotatory. This was due to not knowing the nature of the orbitals found. Unfortunately, time became an issue and so this was not completed to the level of analysis hoped. If the experiment was extended, this would be looked into and full analysis would done to explain the driving force for this reaction.

References

↑ Slater, J., A Simplification of the Hartree-Fock Method, MIT, 1950.
↑ Martin, D., Quantum mechanics of diatomic molecules:overlap integrals, coulomb integrals and ab initio calculations on imidogen, Iowa State University Press, 1968, p.168.
↑ Feilchenfeld, H., A Relation Between the Lengths of Single, Double and Triple Bonds, 1959, vol.63
↑ Batsanov, S.S., Van der Waals Radii of Elements, Centre for High Dynamic Pressures, 2001, vol.37.
↑ Rzepa, H., The Aromaticity of Pericyclic Reaction Transition States, Imperial College London, 2007, vol.84

[1] Slater, J., A Simplification of the Hartree-Fock Method, MIT, 1950.

[2] Martin, D., Quantum mechanics of diatomic molecules:overlap integrals, coulomb integrals and ab initio calculations on imidogen, Iowa State University Press, 1968, p.168.

[3] Feilchenfeld, H., A Relation Between the Lengths of Single, Double and Triple Bonds, 1959, vol.63

[4] Batsanov, S.S., Van der Waals Radii of Elements, Centre for High Dynamic Pressures, 2001, vol.37.

[5] Rzepa, H., The Aromaticity of Pericyclic Reaction Transition States, Imperial College London, 2007, vol.84

[1]

[2]

[3]

[4]

[5]