Cope Rearrangement

Throughout this report click on the hyperlinks to view the log file for the relevant calculation.

Optimisation of Reactants and Products

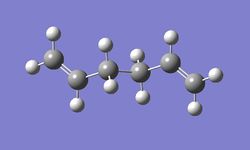
The following anti periplanar and gauche confomers of 1,5-hexadiene was optimised using HF/3-21g level of theory, their energies are tabulated below. (See Appendix 1 for summary table.)

Table 1: HF/3-21G Optimisation of 1,5-Hexadiene Confomers
Confomer	Energy (a.u.)	Point Group
Anti	-231.69254	C_i
Gauche	-231.68961	C1

The resulting structures were then re-optimised under a B3LYP/6-31(d). (See Appendix 1 for summary table.)

Table 2: B3LYP/6-31(d) Optimisation of 1,5-Hexadiene Confomers
Confomer	Energy (a.u.)	Point Group
Anti	-234.5597	C_i
Gauche	-234.609110	C1

Both optimisations confirmed the antiperiplanar conformation (dihedral angle 180^o) had a lower energy than the gauche conformation (dihedral angle 60^o). This in agreement with the hypothesis that the due to steric contraints the gauche conformation will have a greater energy.

The anti2 structure was optimised under a HF/3-21G level of theory to give an energy of -231.69097a.u., and was then reoptimised to the higher level of theory B3LYP/6-31(d) to give an energy of -234.61079.

Sum of electronic and zero-point Energies=           -234.468193
Sum of electronic and thermal Energies=              -234.460941
Sum of electronic and thermal Enthalpies=            -234.459997
Sum of electronic and thermal Free Energies=         -234.499482

Optimisation of Transition Structures

The boat and chair transition states were optimised using a variety of the methods to find the most stable geometry, summary tables of all the calculation can be found in Appendix 1.

Chair

Calculation of Force Constant Matrix

A "guess" structure from two allyl (C₃H₅)was optimised to a TS(Berny) using HF/3-21G level of theory. The terminal carbons were positioned in an eclipsed fashion approximately 2.2Å apart. When using this method of optimisation is particularu important to guess structure is close to the true geometry ensure a successful calculation.

Freezing Reaction Coordinate using Redudant Coordinate Editor

The terminal carbons of the "guess structure" were frozen at approximately 2.2Å apart, and the structure was optimised to a minimum using theHF/3-21G level of theory. The bonds were then unfrozen and optimised to a TS(Berny) using HF/3-21G level of theory.

Table 3: Chair Tranistion States Data
	Hessian	ModRedundant	Combination
Energy (a.u.)	-231.619322	-231.615979	-231.619322
Frequency cm^-1	-817.76	-	-817.81
Bond Length Å C(1)-C(9)	2.02	2.17	2.02
Bond Length Å C(6)- C(14)	2.02	2.2	2.02

Calculation of the hessian and differentiating along the reaction coordinate yeilded similar results, indicating. that the guess structure was close to the true structure. Both techniques are reliable, however as the Modredundant technique is often preferred when the guess structure is more complex.

Boat

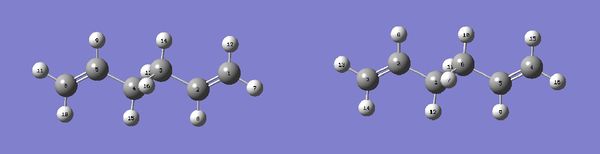
The boat geometry was optimised using the QTS2 method. This technique requires the structures of the reactant and produts (both numbered in the same fashion) and interpolates between them to find the transition state. The anti conformation was numbered in the following way and the TS(QTS2) calculation performed.

Table XX: TS(QTS2) First Optimisation
Input Geometry	Output Geometry

As it can clearly be seen the calculation failed, and the transition structure produced was very similar to the chair geometry. This is because the guess structure was too disimilar from the transition state. A second minimisation was then run after manual modification of the reactant and product to resemble the boat geometry more closely.

Table XX: TS(QTS2) Second Optimisation
Input Geometry	Output Geometry

The resulting tranistion state is the boat structure, hence the manipulation of the reactants and products was necessary.

IRC Calculation

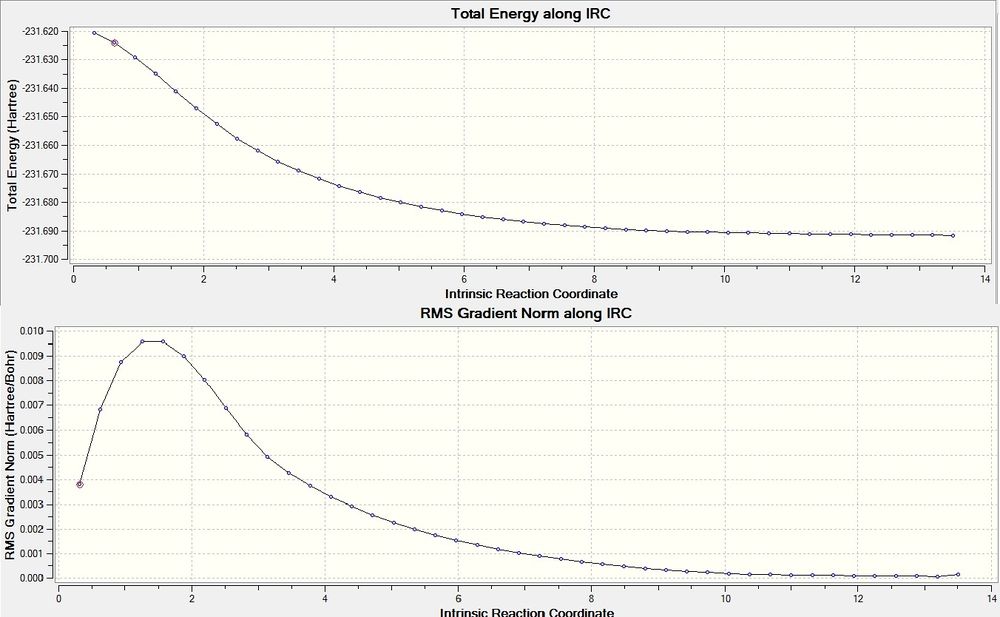
IRC (Intrinsic Reaction Coordinate) calculations are necessary to predict the conformation of the 1,5-hexadiene formed, as the geometry of the transition state is not sufficient. The IRC follows the minimum energy from a given transition state to a product. The optimised chair transition state was further optimised using this technique, the force constant energy was calculated every 10 points up to a maximum of 50. However the calculation stopped at 43 indicating a minimum energy structure had already been obtained.

The final point on the IRC was reoptimised to a minimum under the HF/3-21G level of theory, decreasing the energy from -231.691530a.u. to -231.691667a.u., confirming the product resulting from the chair tranisition state is the gauche2 conformation.

By looking at the log file it is clear the calculation converges to find a minimum energy, hence confirming the transition state.

Item               Value     Threshold  Converged?
Maximum Force            0.000009     0.000450     YES
RMS     Force            0.000003     0.000300     YES
Maximum Displacement     0.000092     0.001800     YES
RMS     Displacement     0.000035     0.001200     YES
Predicted change in Energy=-1.838680D-09
Optimization completed.
   -- Stationary point found.

Further B3LYP/6-31(d) Optimisation

The boat and chair structures undergo further optimisation under the B3LYP/6-31(d), and the activation energies calculated. The results are shown in the table below. The differences in the energies are significantly different, however the geometries appear to be very similar. Hence it can be concluded that it most efficient to first optimise a given structure at a lower level of the theory, and then reoptimise at a higher level.

(The format of the table was taken from the script)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466703	-231.461343	-234.556982	-234.414934	-234.409011
Boat TS	-231.602802	-231.450930	-231.445301	-234.543093	-234.402342	-234.396006
*Reactant (anti2)*	-231.690970	-231.537850	-231.530962	-234.610789	-234.468193	-234.460941

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.7	43.7	33.4	32.6	33.5 ± 0.5
ΔE (Boat)	54.5	53.8	41.3	40.7	44.7 ± 2.0

Diels Alder Cycloaddition

Cis-butadiene

Table 4: Cis-Butadiene MO Anaylsis
	HOMO	LUMO
Relative Energy (a.u.)	-0.227	-0.030
Classification	Bonding	Antibonding
Symmetry about Vertical Plane	Symmetric	Antisymmetric
Symmetry about Horizontal Plane	Antisymmetric	Antisymmetric
Diagram	Cis-Butadiene HOMO.	Cis-Butadiene LUMO.

The structure of cis butadiene was optimised using an Semi-Empirical/AM1 level of theory, resulting in an overall energy of 0.0487972a.u.. This structure was re-optimised using B3LYP/6-31G(d) level of theory, resulting in a significantly lower energy of -155.985950a.u (summary tables can viewed in Appendix 2). The B3LYP/6-31G(d)generated the lowest energy hence is the more reliable optimisation technique, and will be used for the following calculations.

Cyclohexene

Energies and MO Analysis

Table 5: Energies of Cyclohexene Transition State
Optimisation Technique	Energy (a.u.)
B3LYP/6-31(d)	-234.54389696
Mod Redundant and B3LYP/6-31(d)	-234.54389648

The cyclohexene transition state was optimised directly from the 'guess' structure, and then again using the ModRedundant technique (the newly forming σ bonds frozen at approximately 2.2Å), the results are shown in table XX. The mod redundant technique resulted in a slightly lower energy, and hence more stable transition state, this structure undergoes further MO analysis shown in Table6.

Table 6: Molecular Orbitals of the Cyclohexene Transition State
	HOMO	LUMO
Relative Energy (a.u.)	-0.219	-0.009
Classification	Bonding	Antibonding
Symmetry about Vertical Plane	Symmetric	Symmetric
Symmetry about Horizontal Plane	Antisymmetric	Antisymmetric
Diagram	HOMO of Cyclohexene Transition State.	LUMO of Cyclohexene Transition State.

Bond Lengths Analysis

Geometry of Cyclohexene Transition State

The standard C-C bond length between two sp³ hybridised Carbon atoms is 1.54Å^[1]. The Van der Waals radius of a carbon atom is 1.70Å^[2], hence when two carbon atoms are 3.4Å apart this distance is the closest two atoms can get colliding without there being bonding interaction. The distance between the two terminal Carbon atoms is 2.27Å, this is significantly shorter than the sum of the Van der Waals radii, however is not recognised as a formal bond, hence it can be said there is bonding interaction, indicating the formation of the two new σ bonds. The standard C=C bond length between two sp² hybridised Carbon atoms is 1.34Å ^[1]. The length of the C=C bonds in the tranisition state are 1.38Å and 1.39Å, this lengthening is in accordance with the formation of a C-C bond between two sp³ hybridised Carbon atoms.

Vibration Analysis

The computed imaginary frequency exhibits the molecule vibrating in a synchronous motion, which confirms the predicted concerted syn cylcoaddition mechanism. In contrast the lowest positive frequency demonstrates the translational asynchronous motion.

Vibrations of Cyclohexene Transition State
Imaginary Frequency =-525.23cm^-1	Lowest Positive Frequency = 135.73cm^-1

Regioselectivity of Diels Alder

Diels Alder Cycloaddition can proceed via an Exo or Endo mechanism:

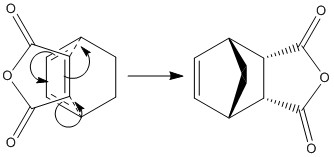
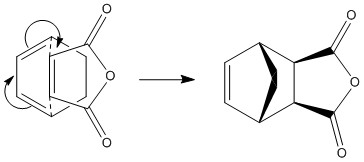
Using B3LYP/6-31(d) optimisation the endo transition had a total energy of -612.683397a.u. , and the exo transition state had a total energy of -612.679311a.u. .

The endo adduct is lower in energy than the exo adduct; and as the endo product has been shown to be the major product this confirms that the reaction is under kinetic control.

Endo

Exo

Structure

Geometry of Cyclohexene Transition State

Energy (a.u.)

-612.683397a.u.

-612.679311a.u.

Distance Between O=C-O-C=O
fragment and "Opposite" C/Å

3.14

2.53

Partially Formed C-C σ Bond/Å

2.27

2.29

Steric Analysis

Through analysis of the bond lengths it is clear the exo transition state is subject to significantly greater steric strain, accounting for its relative instability. The distance between O=C-O-C=O and the 'opposite' Hydrogen of the CH2-CH2 moiety of the diene is 0.61Å closer than the equivalent distance to the CH-CH moiety of the endo adduct. This strain is particularly large, as this C-H distance in the exo transition state is less than the sum of the Van Der Waals radius (2.79Å^[3] resulting in orbital replusion. As a result the C=C of the dienophile is not as proximal, hence the favourable HOMO-LUMO overlap is reduced and the partially formed C-C σ bonds are longer, therefore weaker giving rise to a less stable exo transition state. This structure is a compromise between the optimising the favourable HOMO-LUMO interactions whilst minimising the steric repulsion of the CH2-CH2 and O=C-O-C=O fragments.

Vibration

The table below shows the vibrational animation of both the endo and exo transition states. Each transition states gives rise to one imaginary frequency, confirming the transition state.

Vibrations of Cyclohexene Transition State
Imaginary Frequency =-446.17cm^-1	Lowest Positive Frequency = 448.49cm^-1

Molecular Orbital Analysis

Similarly to the cis-butadiene and ethylene example, the HOMO of the tranistion states are a result of the diene contributing its HOMO, and the dienophile contributing its LUMO to achieve the most effective orbital overlap. Secondary orbital overlap is accountable for the increased relative stability of the endo transition state. As can be seen in the LUMO+1 orbital of the endo adduct, π electrons from the newly forming C=C bond in the diene are donated in the π* C=O orbital of the maleic anhydride. This is possible due to correct symmetry and similar energies, resulting in effective orbital overlap between the π and π* orbitals. The resulting endo transition state is therefore stabilised. In the case of the exo adduct, such orbital overlap is impossible as the C=O π* are on the opposite side of the molecule, hence the exo adduct does not benefit from any secondary orbital stabilisation. This secondary orbital overlap also accounts for the shorter partially formed C-C bond.

By examination of the HOMOs, it is clear the endo structure has a higher electron density at the O=C-O-C=O moiety,

	Endo	Exo
HOMO	Relative Energy = -0.24223a.u. Antisymmetric	Relative Energy = - 0.24216a.u. Antisymmetric
LUMO	Relative Energy = -0.06782a.u. Antisymmetric	Relative Energy = - 0.07840a.u. Antisymmetric
LUMO+1	Relative Energy = -0.05265a.u. Symmetric	Relative Energy = - 0.05188a.u. Symmetric

Conclusion

Throughout this exercise many different optimisation techniques have been employed, it is clear that the use of one single technique is insufficent. It is much more computationally efficient to optimise at a lower level of theory and continue further optimisations at higher levels of theory. Methods such as IRC can then be used to confirm the geometry of the structures.

Appendix 1

Anti Summary
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.6925353a.u.
RMS Gradient Norm	0.00001891a.u.
Imaginary Frequency
Dipole Moment	0 Debye
Point Group	C_i

Gauche Summary
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.6896157a.u.
RMS Gradient Norm	0.00001053a.u.
Imaginary Frequency
Dipole Moment	0.4439 Debye
Point Group	C₁

Anti2 Summary
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G
Charge	0
Spin	Singlet
Total Energy	-234.55970423a.u.
RMS Gradient Norm	0.0000135a.u.
Imaginary Frequency
Dipole Moment	0 Debye
Point Group	C_i

Chair Hessian Optimisation
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.6193223a.u.
RMS Gradient Norm	0.00003503a.u.
Imaginary Frequency	-817.76cm^-1</sup.
Dipole Moment	0.0009 Debye
Point Group	C1

Chair ModRedundant Optimisation
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.61597903a.u.
RMS Gradient Norm	0.00333031a.u.
Imaginary Frequency	-
Dipole Moment	0.0073 Debye
Point Group	C1

Chair Combination Optimisation
File Type	.chk
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.61932232a.u.
RMS Gradient Norm	0.00003475a.u.
Imaginary Frequency	-817.81cm^-1</sup.
Dipole Moment	0.0009 Debye
Point Group	C1

Appendix 2

Cis-Butadiene Summary
File Type	.chk
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(D)
Charge	0
Spin	Singlet
Total Energy	-155.98594952a.u.
RMS Gradient Norm	0.00005672a.u.
Dipole Moment	0.085 Debye
Point Group	C_2v

References

↑ ^1.0 ^1.1 I. Alborta, I. Rozas and J. Elguero, Structural Chemistry, 1998, 115(4)
↑ A. Bondi, J. Phys. Chem., 1964, 68(3)
↑ R. Scott Rowland and R. Taylor, J. Phys. Chem, 1996, 100(18), 7384-7391

[Bond_Legnths-1] 1.0 ^1.1 I. Alborta, I. Rozas and J. Elguero, Structural Chemistry, 1998, 115(4)

[VDW-2] A. Bondi, J. Phys. Chem., 1964, 68(3)

[3] R. Scott Rowland and R. Taylor, J. Phys. Chem, 1996, 100(18), 7384-7391

[1]

[2]

[3]