Rep:Mod:angrychicken
Introduction
Pericyclic Reactions
The Woodward-Hoffmann rules are employed by organic chemists to explain stereospecificity of pericyclic reactions under thermal control. The Woodward-Hoffmann states: [1]
In an open-chain system containing 4n π-electrons, the symmetry of the highest occupied ground-state orbital is such that a bonding interaction between the termini must involve overlap between orbital envelopes on opposite faces of the system. Conversely, in open systems containing 4n + 2 π-electrons, terminal bonding interaction within ground-state molecules requires overlap of orbital envelopes on the same face of the system.
K. Fukui also discovered that orbital overlapping is maximised in a majority of pericyclic reactions [2] that have concerted electronic transfer leading to and after the transition state. An alternative approach to the selectivity of pericyclic reactions were developed by Mobius and Huckel, which along other publications, suggested a symmetrical and aromatic transition state.

Computational chemists in the 1980s entered into an argument suggesting whether the transition state of the Diels-Alder reaction favoured a synchronous or non-synchronous transition state. Experimental and theoretical calculations led to the conclusion that the synchronous concerted mechanism had a lower-energy pathway. [3]

In the case of the Cope rearrangement, an example of sigmatropic reaction, the synchronicity of the transition state is shown to largely depend on substituents. To date, the transition state of an unsubstituted reaction of 1,5-hexadiene is commonly accepted to be synchronous. [4]
12:58, 5 November 2015 (UTC) Very nice intro, you have clearly gone beyond the script and researched literature
Computational Chemistry Methods
Hatree and Fock, two pioneers in computational chemistry, introduced the Hatree-Fock method that represent independent electrons inside an averaged potential in a molecule. The electrostatic repulsion of charge densities of electrons is taken into account, but quantum effects from the Pauli exclusion principle is disregarded. [5] After an initial guess at molecular orbitals, solution of single-particle Schrodinger equations are resolved to form a more accurate set of orbitals. The whole procedure is repeated until energy functions converge to a minimum, exercising the variational principle.
The requirement for computing individual wavefunctions proved to be too expensive for some large molecules. Semi-empirical methods, based on the Hatree-Fock framework, obtains a set of parameters fitted to accurately represent real-world data, and uses parameters to reduce computing time. One needs to be careful deciding on semi-empirical method, as results can be very far from reality if the molecule is too different from ones used in the parameterisation. Here, the AM1 method is used to approximate transition states for the benefit of reduced computing time. AM1 is based on the neglect of diatomic differential overlap (NDDO) which overlooks the overlap integral S. [6]
The Density Functional Theory (DFT) uses the variational principle to minimise the energy Schrodinger equation as a functional in terms of charge densities, which is spatially dependent on the external potential. It has grown to be very popular due to its accuracy.
Computations for energy and geometry of a molecule are based on linear combinations of basic Gaussian functions. Basis sets of the valence shell of the bonding atom are invoked in such computations. Atomic orbitals described by hybridization theory are not sufficient to produce an accurate picture of a molecule since the molecular environment induces spatial asymmetry around the atom. In practice, each sub-orbital is provided with a basis set to allow angular momentum components in computational chemistry. The level of such polarization can be increased at the expense of computation time by including d functions in the basis set. These split-valence basis sets are denoted by x-yzG, where x is the number of primitive function covering each valence orbital and y,z describe the nature of the primitive function.
Nf710 (talk) 13:02, 5 November 2015 (UTC) very good understanding, however the basis set is applied over the whole molecule not just the orbitals. But very good knowledge. Its impressive to see how you know DFT is made up of gaussian functions and that HF uses a mean field potential.
The Cope Rearrangement
Conformers of 1,5-hexadiene
There are three free rotating C-C bonds in 1,5-hexadiene. Steric consideration suggests c-cis conformations will bring vinyl hydrogens too close together, creating strong repulsion. Therefore such conformations shall be disregarded as they are thermodynamically unfavourable. Starting with antiparallel vinyl groups, we gain 2 gauche conformers (A, C) and 1 anti conformer (B). Rotating one of the sp3C - sp2C bonds gives three more conformers, D, E, F, with C=C bonds point at each other.
As the tutorial appendix suggests a very small energy gap between conforms and low level of symmetry, I used a more comprehensive basis set and a more accurate method to probe the order of conformers. All calculations in this section were carried out by the Gaussian 09W program with 6-311G(d,p) basis set using the DFT/B3LYP method. This method was used also for convenient comparison with literature as DFT 6-31G(d) is a very common basis set in reports. Attempts to optimise c-cis conformations in Gaussian generated lower-energy counterparts that have either antiparallel or parallel vinyl groups, implying repulsion between hydrogen atoms is the main factor here.
| Antiparallel Vinyl Groups | Parallel Vinyl Groups | |||||||
|---|---|---|---|---|---|---|---|---|
| Conformer | Point Group | Log File | Energy (Hatree) | Conformer | Point Group | Log File | Energy (Hatree) | |
| Gauche | 
|
C1 | Conformer A | 0.00184 | 
|
C2 | Conformer D | 0.00076 |
| Anti | 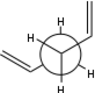
|
C2 | Conformer B | 0 | 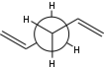
|
Ci | Conformer E | 0.00011 |
| Gauche | 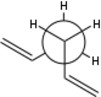
|
C1 | Conformer C | 0.00166 | 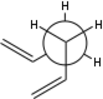
|
C2 | Conformer F | 0.00076 |
Energy values are relative to the lowest-energy conformation, conformer B (-234.6260059 Hatree relative to ZPE) here and from now on in this section.
We can see that steric repulsion raise energy as the sp2-sp3 C bond is rotated and hydrogen atoms get closer, which is true for both gauche and anti conformations. Here, the anti form is consistently lower in energy for all orientations of vinyl groups, which is expected due to sterics.
The energy gaps between these conformers are so small that they are overwhelmed by ambient thermal energy. Thermochemistry output from Gaussian suggests that the thermal correction to energy at 298K is around 0.16 Hatree. This correction is the sum of energies due to electronic, rotational and vibrational motion calculated by their relevant partition functions. Gaussian also gives the thermal correction to enthalpy also includes the Boltmann energy distribution, kBT.
Nf710 (talk) 16:33, 5 November 2015 (UTC) There are several issues here: firstly you have ran it at a basis which is much higher than what was requested. I have given you extra marks for this, however it is interest as all the papers that I have see for this run at 6-31G(d) show your conformer D (F) at the lowest energy due to inphase interactions between the two pi bonds. I would like to have had a look at your .chk files to look at the orbitals themselves. It is interesting to see how the conformers have switched in energy i would not have expected this but have given an extra mark for trying. and the two conformers are the same energy so this backs your cause. It would have been much better if you would have been able to compare these to a lower basis set and compare orbitals to give a good argument. Your use of newman projection is good.
Nf710 (talk) 16:33, 5 November 2015 (UTC) However you have failed to do many things on the mark scheme. you havent done a frequency calculation to prove that it is minimum. you havent compared the geoms for the anti 2 HF/3-21g level, and then at B3LYP/6-31g* level. And you have barely mentioned the thermochemistry, even though your knowledge of stat mech seems to be very good.
The Chair Transition State
A chair C2h structure was constructed as an approximate structure for the Berny algorithm, which found a C2h transition state with 2.02071 Å and 1.96569 Å between allyl groups under the 3-21G basis set and the 6-31G(d) basis set, respectively
Using the ModRedundant Gaussian option, the chair transition state was optimised with allyl group separation frozen at 2.02 Å, followed by a guess Hessian differentiating along the z-axis.
| Allyl Group Separation (Å) | ||
|---|---|---|
| Restricted HF 3-21G Basis Set | DFT/B3LYP 6-31G(d) Basis Set | |
| TS2 Berny | 2.02071 | 1.96569 |
| ModRedundant | 2.02074 | 1.96525 |
The synchronicity of the chair transition state suggests an aromatic transition state and conforms to the Woodward-Hoffman description that allowed a concerted σ bond shift.
Nf710 (talk) 16:38, 5 November 2015 (UTC) This is all excellent theory but you havent run a frequency analysis to check it is a TS.To get an imaginary vibration
The Boat Transition State
The QST2 method was employed to interpolate a starting structure and a product towards the actual transition state, performing algorithms to approach the transition state region. When the thermodynamically favourable conformer B was inputted, the result resembled a chair, which seems to suggest that the chair is the lower-energy saddle point. The structures were edited to look boat-like, with C2-C3-C4 and C3-C4-C5 angles at 100 degrees in order to "brute-force" a boat-like transition state. This successfully resulted in a C2h boat-like transition state and also implies a flat potential energy surface because the transition state largely depends on the starting point and end point.
The distances between the two terminal allyl carbons differ, with the longest at 2.13995 Å and shortest at 2.13989 Å (Restricted HF 3-21G, Log File). The electronic structure of this transition state has more strongly anti-bonding interactions between the central atoms, judging by the appearance of its MOs.
Nf710 (talk) 16:40, 5 November 2015 (UTC) very good that you investigated the MOs to see which one is more antibonding but you again havent checked its imaginary frequency
Reaction Profiles
Intrinsic Reaction Coordinate (IRC) calculations were run on chair and boat transition states and both led to conformer A.
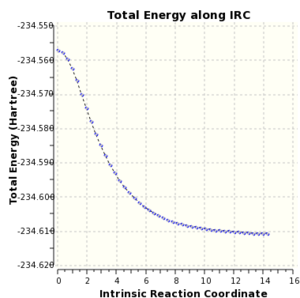
|
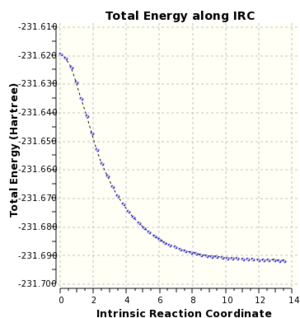
|
| Boat IRC Energy Profile
DFT/B3LYP 6-31G(d) |
Chair IRC Energy Profile
DFT/B3LYP 6-31G(d) |
|---|
Due to the symmetry of this reaction, the activation energy should be identical in magnitude to the stabilisation energy and the enthalpy of reaction is zero. The following values were calculated from the optimisations of Conformer A and the transition states with the DFT/B3LYP method and 6-31G(d, p) basis set:
| ΔE‡ (0K, Hatree)
Eelec + ZPE |
ΔH‡ (298K, Hatree)
Etot + kBT | |||
|---|---|---|---|---|
| Computed | Literature | Computed | Literature | |
| Chair | +0.054318 | +0.05482[7] | +0.052896 | +0.052908[7] |
| Boat | +0.070717 | +0.07123[8] | +0.069294 | N/A |
| Experimental | N/A | +0.53386[9] | ||
Although no 6-31G(d) literature was available for the boat structure, one article using the 6-31G(d, p) did confirm that boat transition state lies higher in energy by 0.01147 Hatrees[10] (at 298K), similar to the 6-31G(d) result. Experimental data confirms that the chair is the preferred transition state both by activation enthalpy and isotopic studies [11].
From frontier orbital theory, it is the anti-bonding overlap between the central carbon atom that destabilise the system[12]. The central carbon atoms are closer in the boat geometry, which is incidentally the higher-energy transition state.
Nf710 (talk) 16:49, 5 November 2015 (UTC) Be carefull when comparing other basis sets especially for absloute energy. But you have found lots of literature which is excellent. You have compared the geoms for both. Again you forgot to check for an imaginary frequency. your use of MOs to explain the differences in energy and literature references are particularly exceptional.
Nf710 (talk) 16:55, 5 November 2015 (UTC) You are clearly a very talented computational chemist, your knowledge of computational methods is very good for a 3rd year, you have kept it concise clear. But you you havent followed the lab script at all at parts and unfortunately that meant that you lots marks which were very easy marks. I will try to give you some extra marks for your very good understanding of the theory to make up for this. but in future follow the lab script where its says, then try to go further after you have done all the elementary things
Diels-Alder Cycloaddition
Diels-Alder additions are pericyclic and result in the forming of two new sigma bonds at the expense of one pi bond.
First, we used a relatively simple cycloaddition to probe the geometry of the transition state:
Stereoselectivity issues arise when we move some symmetry in the dienophile:
Geometry of the Transition State
Molecular orbital calculations were carried out for ethene, cis-1,4-butadiene with DFT/B3LYP 6-31G(d) and Restricted HF 3-21G*.
The transition state geometry was determined using the TS2 Berny algorithm using two different basis sets. Only one imaginary frequency was found, implying that the structure is the actual energy saddle point. The transition state was of point group Cs and symmetrical with respect to the plane intersecting C1-C2 and C4-C5:
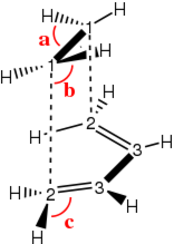
| Structure (Method) | C1-C1
distance (Å) |
a
(°) |
C1-C2
distance (Å) |
b
(°) |
C2-C3
distance (Å) |
C3-C3
distance (Å) |
c
(°) |
Log Files |
|---|---|---|---|---|---|---|---|---|
| TS (Restricted HF 3-21G*) | 1.37585 | 120.6 | 2.20953 | 89.1 | 1.36999 | 1.39445 | 120.5 | Transition state |
| Reactant (DFT/B3LYP 6-31G(d)) | 1.33087 | 120.0 | N/A | N/A | 1.33993 | 1.47138 | 122.5 | Ethene; cis-butadiene |
| TS (DFT/B3LYP 6-31G(d)) | 1.35643 | 119.8 | 2.26100 | 91.8 | 1.35354 | 1.41344 | 120.0 | Transition state |
| Product (DFT/B3LYP 6-31G(d)) | 1.56148 | 110.5 | 1.55453 | 108.0 | 1.51362 | 1.31780 | 111.3 | cyclohexene |
The π-bonds in the reactants have stretched by just <0.02 Å in the transition state and still roughly 120°, retaining most of its π-character . The C3-C3 bond is yet to have much of a π-character, judging by its bond length. The C1-C3 distance is longer than typical sp3-sp3 carbon bond lengths (roughly 1.54 Å) but significantly lower than the sum of the Van der Waals radii of the two carbon atoms (3.40 Å), raising energy by electronic repulsion. In conclusion, the sigma framework is incomplete and the π interactions are in place in the transition state. This indicates that this Diels-Alder cycloaddition has an early transition state, in line with Hammond's postulate (exothermic reactions have early transition states and vice versa).
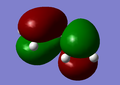
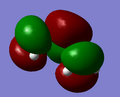
The symmetry of the LUMOs and HOMOs matches the Woodward-Hoffmann description of pericyclic reaction, as the HOMO has orbital overlap on the same face of the system with 4n + 2 electrons (n=2).
-
HOMO of butadiene is antisymetric with respect to plane.
-
LUMO of butadiene is symmetric with respect to plane.
-
HOMO of the transition state is antisymmetric with respect to the plane intersecting C1-C1.
-
LUMO of the transition state is symmetric with respect to the plane intersecting C1-C1.
(You should include the MOs of Ethylene and state which MOs of Ethylene and Butadiene have been used to form the MOs of the TS Tam10 (talk) 12:51, 28 October 2015 (UTC))
The TS2 Berny transition state has a synchronous imaginary vibrational mode, leading to a concerted bond formation mechanism, which is confirmed by IRC calculation as well. The transition has a positive-frequency vibrational mode with an asynchronous sigma bond formation , implying that there exists a higher-energy saddle point, on which the transition state is not converted.
(This is not really the case. The reaction will not occur through this positive frequency. Instead it indicates that at the transition state, it is stable with respect to this normal mode Tam10 (talk) 12:51, 28 October 2015 (UTC))
(I can't see a mention as to whether this reaction is allowed or forbidden Tam10 (talk) 12:51, 28 October 2015 (UTC))
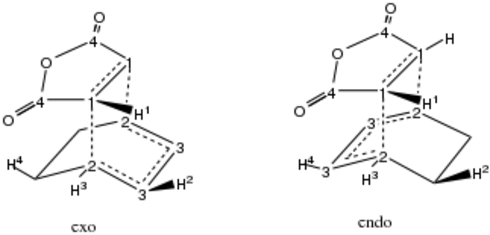
Stereoselectivity: Exo versus Endo
Reactants maleic anhydride and cyclohexa-1,3-diene were optimised separately and then brought together to build rough estimates of endo and exo geometries. The corresponding stereoisomeric products were built and appended to the molecule group for QST2. QST2 was the method of choice because I was not confident that the starting structure was an accurate description of the transition state due to the complex nature of the transition state, which was especially true for the endo stereoisomer. This time I did not perform IRC analysis because IRC computing time for a molecule this complex can take very long, and because there was no confusion to the conformation or stereoisomerism of the product since the correct endo or eco product was submitted in QST2.
| Structure | (Hatree) relative to ZPE | Log Files | ||||
|---|---|---|---|---|---|---|
| AM1
Eelec |
AM1
Etot + kBT |
DFT/B3LYP 6-31G(d)
Eelec |
DFT/B3LYP 6-31G
Etot + kBT | |||
| maleic anhydride | -0.063346 | -0.058193 | -379.231570 | -379.226487 | (1) | AM1; DFT |
| cyclohexa-1,3-diene | -231.451337 | -231.445649 | -233.296216 | -233.291041 | (2) | AM1; DFT |
| endo transition state | 0.133494 | 0.143683 | -612.517672 | -612.507313 | (3) | AM1; DFT |
| exo transition state | 0.134882 | 0.144883 | -612.198004 | -612.487667 | AM1; DFT | |
| endo Diels-Alder adduct | 0.031461 | 0.040459 | -612.572077 | -612.562626 | (4) | AM1; DFT |
Experiments suggest that kinetics is the reason for the stereoselectivity in this irreversible and highly exothermic Diels-Alder reaction. However, the AM1 semi-empirical method suggests a highly endothermic reaction, which is definitely not the case and could be blamed on the inability of AM1 to accommodate for heteroatoms since the AM1 electronic energy for maleic anhydride is almost at ZPE. AM1 was used as a first approximation in order to reduce computing time, but seeing this large inaccuracy, the AM1 data shall be dismissed in this cycloaddition. Alternatively, the anomaly could be due to my own mistakes. I carried on using DFT/B3LYP 6-31G(d) level of theory to produce more accurate thermodynamic data that could be compared with both empirical and theoretical results in literature.
Calculations using AM1 and DFT/B3LYP 6-31G(d) agree with the stereoselectivity in that the endo transition state lies lower in energy than the exo transition state:
| Stereoisomer (Method) | (Hatree) relative to ZPE | ||||
|---|---|---|---|---|---|
| ΔE‡
(3) - [(1) + (2)] |
ΔH‡
(3) - [(1) + (2)] |
ΔEstabilisation
(4) - (3) |
ΔHstabilisation
(4) - (3) |
ΔHreaction
(4) - [(1) + (2)] | |
| endo (AM1) | +231.4419737 | +231.647525 | -0.103421 | -0.104424 | +231.647525 |
| endo (DFT/B3LYP 6-31G(d)) | +0.010114 | +0.010215 | -0.074073 | -0.074959 | -0.045098 |
| exo (AM1) | +231.4433617 | +231.647525 | N/A | N/A | N/A |
| exo (DFT/B3LYP 6-31G(d)) | +0.029782 | +0.029861 | N/A | N/A | N/A |
| endo
(experimental, in benzene) |
N/A | +0.018645
± 0.00096[13] |
N/A | -0.022310
(calculated) |
-0.003665[13] |
(This table is pretty hard to understand. You should convert your units (for activation and reaction energies) into kcal/mol or kJ/mol Tam10 (talk) 12:51, 28 October 2015 (UTC))
The DFT/B3LYP 6-311G(d) result is not without fault, either: the calculated enthalpy of activation is only half of the experimental result. Enthalpies of activation and reaction are both more negative than experimental data by roughly the same amount, which implies that the energy calculations for the transition state and the adduct are accurate, and that the starting structure energies are more positive than reality.
There is indeed one factor that explains the phenomenon: the benzene solvent lowers the energies of reactants with its conjugated π system. The adduct, on the other hand, has only one π bond and is poorly solvated. It will be interesting to see how much of the 0.0008 Hatree difference is due to solvent effects. (One Japanese paper analyses the kinetics of this reaction under vacuum, but it is not accessible because the college does not subscribe to the journal.)
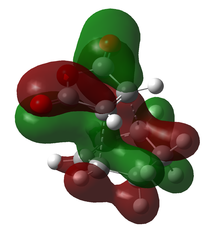
Secondary Orbital Overlap Effect
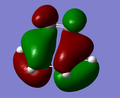
In the DFT/B3LYP 6-31G(d) optimization, the endo approach lowered the energy by 0.019646 Hatree. It has been theorized that the difference is caused by secondary orbital overlap. Features of such overlap can be seen in the HOMO and MOs that lie relatively deep in the endo transition structure, which is only possible due to the orientation of the π systems.
However, bond strain also contributes to this energy difference between endo and exo:
| Separation between atoms | (Å) | ||
|---|---|---|---|
| exo | endo | Sum of VdW radii | |
| C1-C2 | 2.29226 | 2.26784 | 3.40 |
| (C=)O-H4 | 2.80636 | 3.40529 | 2.72 |
| H1-H2 | 3.05024 | 2.34563 | 2.40 |
| H1-H3 | 2.63473 | 2.61372 | 2.40 |
It is clear that the endo structure has significantly more strain in three out of the four cases. O-H4 is the only time when endo is expected to do better due to the planarity of C3, but the exo O-H4 separation is lower than VdW radii, meaning that this does not cause strain in either cases. The main clash here is the H1-H2 distance. Despite the steric strain, the endo transition structure is still lower in energy, implying that electronic stabilisation gained from secondary overlap effect dominates steric effects.
Conclusion
I have shown that computational chemistry can predict an accurate picture of the transition state, and explain, using MOs and energies, the reactivity of some pericyclic reactions. However, it is difficult to pinpoint energy gaps and orbital coefficients to a single factor, even in computational chemistry. Another weakness of this approach is that it only simulates one molecule, but the environment around it could change the reaction considerably, as shown in many cases, and here in the benzene-solvated Diels-Alder example.
Due to time constraints, I was not able to investigate when Diels-Alder reactants have different substituent groups. Undertaking substituted versions of dienes and dienophiles require much more computing time. But computing these interactions can be very revealing since the frontier orbital theory predicts that energies of HOMO and LUMO are substantially affected by adding electron-withdrawing and electron-donating substituents. The coefficients of the frontier orbitals predict the regioselectivity of the reaction.
References
- ↑ R.B. Woodward, R. Hoffmann, J. Am. Chem. Soc., 1965, 87(2), 395–397, doi:10.1021/ja01080a054
- ↑ K. Fukui, Acc. Chem. Res., 1971, 4, 57, doi:10.1021/ar50038a003
- ↑ Y. Li., K.N. Houk, J. Am. Chem. Soc., 1993, 115(16), 7478-7485, doi:10.1021/ja00069a055
- ↑ O. Wiest, K.A. Black, K.N. Houk, J. Am. Chem. Soc., 1994, 116(22), 10336-10337, doi:10.1021/ja00101a078
- ↑ M.Y. Amusia, A.Z. Msezane, V.R. Shaginyan, Physica Scripta, 2003, 68(6), 133-140, doi:10.1238/Physica.Regular.068aC0133
- ↑ M.J.S. Dewar, D.G. Zoebisch, E.F. Healy, J.J.P. Stewart, J.Am.Chem.Soc., 1985, 107(13), 3902-3909, doi:10.1021/ja00299a024
- ↑ 7.0 7.1 V.N. Staroverov, E.R. Davidson, Jour. Mol. Struct., 2001, 573, 81-89, doi:10.1016/S0166-1280(01)00536-X
- ↑ Third-Year Chemistry Computation Lab Module 3: "The Cope Rearrangement Tutorial"
- ↑ W.v.E. Doering, V.G. Toscano, G.H. Beasley, Tetrahedron, 1971, 27, p.5299
- ↑ K.A. Black, S. Wilsey, K.N. Houk, J. Am. Chem. Soc., 2003, 125, 6715-6724, doi:10.1021/a021330h
- ↑ J.J. Gajewski, N.D. Conrad, J. Am. Chem. Soc., 1979, 101, p.6693
- ↑ Ian Fleming, "Frontier Orbitals and Organic Chemical Reactions", 1976, Wiley, 107-108
- ↑ 13.0 13.1 B. Eisler, A. Wassermann, J. Chem. Soc., 1953, p.979-982, doi:10.1039/JR9530000979