Rep:Mod:andyr2911
The Cope Rearrangement
The [3,3]-sigmatropic shift of 1,5-hexadiene was studied and the objective was to locate the low-energy minima and the transition structure on this compound, in order to determine the preferred mechanism.
There has been great interest in investigating the study of the mechanism. The mechanism (concerted,stepwise or dissociative) has been long debated. However, it has been widely accepted that the reaction proceeds in a concerted mechanism for the rearrangement. The reaction proceeds via the "boat" and "chair transition states structure. The B3LYP/6-31G* level of theory has been proven to be exceptional in giving activation energies and enthalpies which is concordant with the experiment determined values. This is a concise report on the location of the transition structures and low energy minima on the 1,5-hexadiene's potential energy surface. These results show the preferred transition structure for the mechanism for the Cope-rearrangement.
Optimisation of an "anti" and "gauche" linkage 1,5-hexadiene
| Calculation Information | Anti 2 | Gauche 5 |
|---|---|---|
| Calculation type | FOPT | FOPT |
| Calculation Method | RHF | RHF |
| Basis Set | 3-21G | 3-21G |
| Total Energy (a.u) | -231.69253528 | -231.68961573 |
| RMS Gradient Norm (a.u.) | 0.00001891 | 0.00001489 |
| Point Group | C1 | C2 |
Using GaussView, 1,5-hexadiene was drawn with an "anti" linkage, approximately an anti-periplanar conformation. The structure was cleaned using the clean function and was optimised at the HF/3-21G level of theory. This was symmetrised and anti conformer was obtained with C1 symmetry and an electronic energy of -231.693 (Units? João (talk) 15:43, 14 April 2015 (BST)) which is concord with the literature value (Reference? Is this value obtainable experimentally? If a calculation, of what type? João (talk) 15:43, 14 April 2015 (BST)). This was found to be the anti 2 conformer. The above method was applied in the same fashion to a "gauche" conformation of 1,5-hexadiene.The point group was identified to be C2 and the electronic energy was -231.690. This was confirmed to be the gauche 5 conformer.
The anti conformer generated was predicted to have a lower energy due to less steric hindrance. Despite the anti conformers being generally lower than the gauche conformers, Gauche 3 has the lowest energy conformer. This arises due to the attractive interaction between an ethenyl proton and the pi orbital [1]. The Ci anti 2 conformation of 1,5-hexadiene was optimised at HF/3-21G level of theory and its final energy was compared to B3LYP/6-21G* level of theory. This differences are observed in the table:
| Calculation Information | Anti 2 HF/3-21G | Anti 2 B3LYP |
|---|---|---|
| Calculation type | FOPT | FOPT |
| Calculation Method | RHF | RB3LYP |
| Basis Set | 3-21G | 6-31G* |
| Total Energy (a.u) | -231.69253538 | -234.55970458 |
| RMS Gradient Norm (a.u.) | 0.00001893 | 0.00004327 |
| Point Group | Ci | Ci |
The molecular structures have not changed and this was observed by looking at the bond lengths and angles which were similar with respect to one another. The electronic energy for the B3LYP/6-31G* level of theory was higher than the HF/3-21G (It is actually smaller, but that is not significant as it is meaningless to compare absolute energies calculated with different methods, and such energy is not experimentally obtainable. One can only compare relative energies. João (talk) 15:43, 14 April 2015 (BST)). The higher level of theory is more accurate because it includes polarisation and the nature of the core electrons is improved (Also valence electrons are better described. Apart from the basis set you also use a different method, do you expect improvements with respect to a HF/6-31G* level of theory? João (talk) 15:43, 14 April 2015 (BST)). Therefore it is concluded that 6-31G* is more accurate than 3-21G (Do you actually have evidence of this conclusion or this is something you expect a priori? João (talk) 15:43, 14 April 2015 (BST)). [2]
Frequency calculation was examined on the anti 2 conformer for the optimised B3LYP/6-31G* structure. It was observed that the vibration frequencies were all positive and this suggests that the conformer has a local minimum electronic energy. The IR spectrum was plotted:
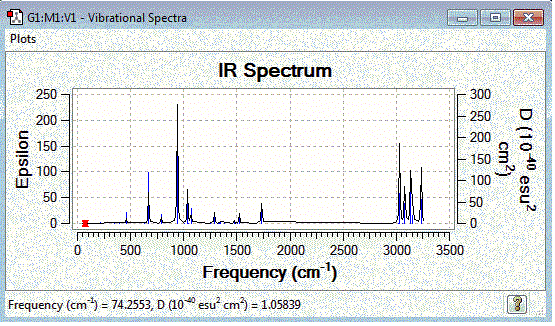
|
The thermochemistry data: (At 0K how would these values change? João (talk) 15:43, 14 April 2015 (BST))
| Sum of electronic and zero-point Energies (a.u) | -233.269204 |
|---|---|
| Sum of electronic and thermal Energies (a.u) | -233.261657 |
| Sum of electronic and thermal Free Energies (a.u) | -233.427768 |
Optimising the "Chair" and "Boat" Transition Structures
An allyl fragment CH2CHCH2 was drawn on Gaussview and optimised using HF/3-21G level theory. (Is the point group of your optimized allyl fragment what you expected to be? Thinking in terms of hybridized orbitals, what orbitals would be involved in the conjugated π bond? João (talk) 15:43, 14 April 2015 (BST))
| Calculation Information | Allyl fragment HF/3-21G | Chair TS HF/3-21g | Boat TS QST2 |
|---|---|---|---|
| Calculation type | FOPT | FOPT | FOPT |
| Calculation Method | RHF | RHF | RHF |
| Basis Set | 3-21G | 3-21G | 3-21G |
| Total Energy (a.u) | -115.59490537 | -231.4794963 | -231.61932213 |
| RMS Gradient Norm (a.u.) | 0.00005281 | 0.01935506 | 0.00003967 |
| Dipole Moment (Debye) | 0.0698 | 0.1039 | 0 |
| Point Group | C2V | C1 | C2H |
The optimised allyl fragment was copied twice into a new window and were orientated so that they look similar to the chair transition state. The terminal ends of the alkene were altered to be 2.2A apart. A Gaussian optimisation was set to TS(Berny) and the force constant calculation was changed to one. "Opt=NoEigen" was added to stop the calculation from crashing when more than one imaginary frequency is detected. The imaginary frequency of magniture was calculated to be -817.92cm-1 which is similar to the literature value of -818cm-1 (Reference? Is this quantity measurable experimentally? João (talk) 15:43, 14 April 2015 (BST)).
|
Optimisation of the Chair Transition State using the Frozen Coordinate Method

The Chair Transition State was frozen using the Redundant Coordination Editor and the bond lengths between the terminal allyl carbons was set to 2.2A. The optimisation was performed in the same way as before, with an additional input "Opt=ModRedundant". The resulted in a similar transition structure from before but with fixed bond lengths of approximately 2.2A. (What is the use of performing this calculation? What do you want to achieve? João (talk) 15:43, 14 April 2015 (BST))
Opitimising and Locating the boat transition state
The Ci anti 2 1,5-hexadiene reactant was numbered manually such that it mirrored the product. The boat transition state was located and optimised using the QST2 method instead of TS(Berny). This method generates the transition state by linearly interpolating between the reactants and the products. (Did you directly obtain the boat transition state using the QST2 method starting from the anti reactant/product? How did you proceed? João (talk) 15:43, 14 April 2015 (BST))
|
The imaginary frequency was found to be -839.83 cm-1, indicating that this was a transition state structure.
Intrinsic Reaction Coordinate method
This method allows to follow the minimum energy path from a transition structure down through the local minimum on a potential energy surface. This is achieved by taking small geometry steps at the steepest point in the PES. The reagent and the product are symmetrical thereby IRC was calculated in only the forward reaction. The boat transition state required around 50 number of points to reach the local minimum as its structure was predicted. The calculation itself was large in comparison to the previous optimisation. The transition state was not achieved on completion therefore optimisation under HF/3-21G level of theory was calculated because it is faster (What do you want to obtain by performing an Intrinsic Reaction Path calculation? Is it the same information content than an optimization of a minimum or a transition state? João (talk) 15:43, 14 April 2015 (BST)). Due to time constraint, the force constant could not be calculated at every step.
(What has changed from the previous to the next paragraph? João (talk) 15:43, 14 April 2015 (BST)) The local minimum was achieved before the estimated 50 number of points had completed leading to calculation to terminate. The graphs were plotted by selecting the IRC path. This shows that the minima was reached and both the 'RMS gradient norm' and the 'Total energy along IRC curve' have constant values. The 4th and 5th point were the steepest points.
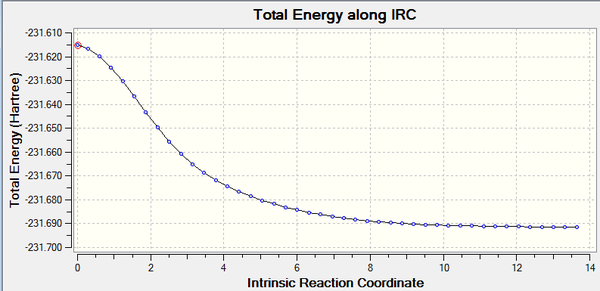
Activation energies of both transition structures
The activation energies for both transition structures were calculated using B3LYP/6-21G* level of theory. The frequency was calculated once it was optimised.
| Calculation Information | Chair TS | Chair TS/6-31G* | Boat TS 3-21G | Boat TS B3LYP/6-31G* |
|---|---|---|---|---|
| Calculation type | FOPT | FOPT | FOPT | FTS |
| Calculation Method | RHF | RHF | RHF | RB3LYP |
| Basis Set | 3-21G | 6-31G* | 3-21G | 6-31G* |
| Total Energy (a.u) | -115.62304009 | -231.52632247 | -231.43132213 | -234.32104499 |
| RMS Gradient Norm (a.u.) | 0.00002734 | 0.00000743 | 0.00003967 | 0.00003460 |
| Dipole Moment (Debye) | 0.0151 | 0 | 0 | 0.1432 |
| Point Group | C1 | C1 | C2h | C2h |
As previously discussed when changing the level of theory, the geometric are similar relative to each other but differ in their electronic energies. This is due to the accuracy of the B3LYP/6-31G* level of theory. (Did you check the obtained structure was a transition state at the new level of theory? João (talk) 15:43, 14 April 2015 (BST))
| Chair TS | Boat TS | Anti-2 conformer | |
|---|---|---|---|
| Sum of electronic and zero-point Energies (a.u) | -233.358204 | -233.34231 | -234.35121 |
| Sum of electronic and thermal Energies (a.u) | -233.358107 | -233.34031 | -233.358116 |
| Sum of electronic and thermal Free Energies (a.u) | -233.410778 | -233.33170 | -233.41082 |
The activation energy was calculated between the difference between the anti 2 conformer electronic energy and the transition state electronic energy. The electronic energies value were computed at 0K. Gaussian automatically corrects to 298.15 K. Herein, 0.1k was used successfully.
| Chair TS | Boat TS | |
|---|---|---|
| Activation energy 0 K (kcal/mol) | 33.556 | 42.562 |
| Activation energy 298.15 K (kcal/mol) | 31.105 | 41.822 |
The chair transition state is preferred to the boat transition state due to the kinetic effects (Not sure I understand what you mean by "kinetic effects". João (talk) 15:43, 14 April 2015 (BST)). Therefore thermodynamic conditions will favour the reaction to proceed via the chair transition state (Does thermodynamics care about the nature of the transition state? João (talk) 15:43, 14 April 2015 (BST)).
(How does your result compare to the experimental values? João (talk) 15:43, 14 April 2015 (BST))
Diels-Alder Reaction
The Diels-Alder reaction is [4n+2] cycloaddition reaction. This involves the formation of new sigma bonds between a diene and a dienophile yielding a cyclohexane product. It is widely accepted that this reaction is a concerted pericyclic reaction. Diels-Alder reactions are stereospecific, it can proceed via two transition states the endo and exo. According to the Frontier Molecular Orbital theory, it is suggested that the stronger the orbital interaction between the dienophile's LUMO and the diene's HOMO, the greater the rate of reaction. However steric play a pivotal role and must be taken into account.
This study shows the transition states for the Diels-Alder reaction between ethylene and cis-butadiene and 1,3-cyclohexadiene and maleic anhydride. Using GaussView, cis butadiene was built and optimised. It was first symmetrised with AM1 semi-empirical MO method to edge towards the transition state. Optimisation using B3LYP/6-31G* level of theory was performed as shown in the table:
| Calculation Information | AM1 Cis-Butadiene | B3LYP/6-31G* Cis-Butadiene |
|---|---|---|
| Calculation type | FOPT | FOPT |
| Calculation Method | RAM 1 | RB3LYP |
| Basis Set | ZDO | 6-31G* |
| Total Energy (a.u) | - | -155.95382679 |
| RMS Gradient Norm (a.u.) | 0.00001745 | 0.00002505 |
| Dipole Moment (Debye) | 0.0414 | 0.0940 |
| Point Group | C2V | C2V |
The same procedure was performed on ethene and the HOMO/LUMO molecular orbitals were observed in Gaussview.
| Molecular Orbital | Image | Symmetry |
|---|---|---|
| Cis Butadiene LUMO |  |
Symmetric |
| Cis Butadiene HOMO |  |
Anti-Symmetric |
| Ethene LUMO |  |
Anti-Symmetric |
| Ethene HOMO |  |
Symmetric |
Computation of the transition state
The transition state structure has an envelope structure and to obtain this geometry was to guess and optimise using the AM1 semi-empirical MO level of theory and then the commonly used B3LYP/6-31G.[3] (It is not clear how you are using AM1 and DFT. Are you optimizing with AM1 and subsequently calculating the energy with DFT? How do you know your structure is optimized at DFT level? João (talk) 15:43, 14 April 2015 (BST)).The calculations proceeded without any errors using the guessed structure. A frequency calculation step was performed, obtaining an imaginary frequency which verifies that this was a transition state structure.The reported values for the average sp3 C-C and sp2 C-C bond length are 1.53A and 1.33A respectively. However the transition state bond length lies in between these values indicating that the carbon atoms has a bond order magnitude between sp2 and sp3 hybridisation. The carbon van der Waals radius is 1.70A. The distance between the terminal carbons is less than twice the VDW radii indicating bonding interaction at the termini. (Where do you show this? João (talk) 15:43, 14 April 2015 (BST))
| Level of Theory | Image |
|---|---|
| Semi-empirical AM1 |  | |
|
| DFT B3LYP/6-31G |  | |
|
(Do the images above correspond to the transition state? One looks like the product and the other butadiene. What is the symmetry of the frontier orbitals of the transition state? From which orbitals are they formed? Why is the reaction allowed? João (talk) 15:43, 14 April 2015 (BST))
Regioselectivity of Diels-Alder
The reaction between maleic anhydride and 1,3-cyclohexadiene gives both endo and expo products. The same methodology previously used was used again to optimise.
| Calculation Information | Maleic Anhydride | 1,3-cyclohexadiene |
|---|---|---|
| Calculation type | OPT+FREQ | OPT+FREQ |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | 6-31G | 6-31G |
| Total Energy (a.u) | -379.29272204 | -233.4279251 |
| RMS Gradient Norm (a.u.) | 0.00003352 | 0.000031937 |
| Dipole Moment (Debye) | 4.0692 | 0.5686 |
| Point Group | C2V | C2V |
| Molecular Orbital | Symmetry with respect to the plane of symmetry |
|---|---|
| Maleic Anhydride LUMO | Symmetric |
| Maleic Anhydride HOMO | Anti-Symmetric |
| 1,3-cyclohexadiene LUMO | Anti-Symmetric |
| 1,3-cyclohexadiene HOMO | Symmetric |
Endo and Exo Transition States
The optimisation was performed in the same manner as previously and it was faster.
| Calculation Information | Endo Transition State Semi-empirical AM1 | Followed by DFT |
|---|---|---|
| Calculation type | FOTP | FREQ |
| Calculation Method | RAM1 | RB3LYP |
| Basis Set | ZDO | 6-31G* |
| Total Energy | -0.15990939 | -612.68339679 a.u. |
| RMS Gradient Norm (a.u.) | 0.00001728 | 0.00001270 |
| Dipole Moment (Debye) | 5.2575 | 6.1144 |
| Calculation Information | Exo TS semi-empirical/AM1 | Followed by DFT |
|---|---|---|
| Calculation type | FOPT | FREQ |
| Calculation Method | RAM1 | RB3LYP |
| Basis Set | ZDO | 6-31G* |
| Total Energy | -0.21387277 | -613.78337132 a.u. |
| RMS Gradient Norm (a.u.) | 0.000015929 | 0.01292432 |
| Dipole Moment (Debye) | 5.5057 | 6.1673 |
-
Exo TS
-
Homo Exo TS
-
Endo TS
-
Homo Endo TS
| Chair TS | Boat TS | |
|---|---|---|
| Activation energy 0 K (kcal/mol) | 18.331 | 20.224 |
| Activation energy 298.15 K (kcal/mol) | 18.405 | 20.224 |
The imaginary frequency for the Endo and Exo transition States were -445,67cm1 and -447,87cm1. The endo product is selectively preferred over the exo product and this is supported by experimental procedures. [4]. It was observed that the endo product was the kinetic product due to the lower activation energy. This can be further explained by the secondary orbital overlap in the transition states. The new pie bond interacts with the orbitails of the carbonyl function group due to the same symmetry further stabilising the transition state.
Conclusions
The transition states were successful and it was concluded that the chair transition state is lower in energy than the boat transition state.
For Diels-Alder cycloaddition reaction, the cis-butadiene and ethylene reaction was analysed and it was concluded through MO the symmetry conditions required for a Diels-Alder cycloaddition. The endo product was favored for the reaction between maleic anhydride and 1,3-cyclohexadiene due to the low activation energy barrier and the secondary orbital effect of the endo transition state.