Rep:Mod:am4011

Physical Computational Laboratory

Introduction

The purpose of this laboratory is to use computational chemical methods to investigate pericyclic reactions and their transition states. We will be using the software Guassview 5.0, which is able to numerically solve the Schrödinger equation for different atoms and molecules using a series of approximations. These approximations can be manipulated by using different quantum mechanical methods, which allows us to have more accurate calculation but are more time intensive. A variety of methods will be seen throughout the procedure. The computational methods allow us to study species that would otherwise be very difficult to study, either because they are too dangerous to work with, or because they exist for such a small amount of time that finding out any information about them would be impossible. Using computational chemistry we are able to invesitgate the properties of transition states, something we would be unable to do in a wet laboratory. Computational methods have also shown to give very good agreement between calculation and experiment, so we can be confident in the results that we have from the experiment. By using Gaussian we can probe well known reactions and discover what is truly happening at the molecular level, whilst also being able to predict a variety of spectroscopic and thermodynamic properties.

The Cope Rearrangement

The Cope Rearrangement is a [3,3] sigmatropic rearrangment of an organic molecule. In this study we will be considering the cope rearrangement of 1,5-hexadiene as shown below:

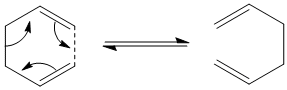
The reaction was reported in 1940 and whilst it may not be the most practically important reaction, the oxy-cope rearrangement is of more synthetic use. The reaction is an example of a pericyclic reaction, that is a reaction which proceeds in a concerted fashion and has a cyclic transition centre. Another characteristic of the pericyclic reaction is that it contains no reaction intermediate. The original studies of pericyclic reactions led to the development of the Woodward-Hoffman rules, a set of rules which tell us whether a pericylic reaction is "allowed" or "forbidden". The aim of this study was to investigate the transition structure of the cope rearrangement of 1,5-hexadiene, as it can take two forms a chair form and a boat form as seen below:

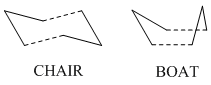
The objective was then to use the information found from the quantum mechanical computational calculations to locate the potential energy minimum of this reaction and thus determine the preferred mechanism of the reaction, by deducing which transition state gave the lowest activation energy to a reaction occuring. We can see that the transition state takes the form of a cyclohexane molecule,and so we can predict that the lower energy activation energy barrier is likely to be for the "chair" form of the transition state. From conformational analysis of cyclohexane we know that this is a lower enegy conformer than the "boat" conformer of cyclohexane, as can be seen below

We can see that there is a difference in energy of ~6.9kcal between the chair and boat conformers of cyclohexane, and so we would reasonably assume that the barrier to activation will be lower for the chair form of the transition state than the boat form.

This reaction involves the rearrangement of the 1,5-hexadiene molecule, therefore in order to calculate the transition state energy and thus the activation energy we must first calculate the energy of the reactant and product.

Calculating the energy of the Reactant

In order to calculate which transition state is the most favourable we must calculate the activation energy for each reaction corresponding to the different transition state, chair or boat. As we have a pericyclic reaction occuring the activation energy for the reaction will simply be the difference in energy between the reactant and the transition state (as the reactant and the product are the same so have the same energy). The procedure therefore involves first calculating the energy of our reactant, 1,5-hexadiene.

At first sight this may seem trivial, why not simply draw 1,5-hexadiene and calculate the energy of the molecule using Gaussian? The problem with this is that we must first find the lowest energy conformation of 1,5-hexadiene as this is the conformation the molecule is most likely to be found in (according to the Maxwell-Boltzmann equation), and so we must ensure that it is this conformation we use in our calculations. However we must of corse first find this calculation by experimenting with the structure in Gaussian, optimising the molecule and recording the energy. The error seems trivial between the lowest and highest energy conformations (< 0.01 a.u) however we must remember that this corresponds to a energy of +60 kJ mol^-1 and so this will leave our final activation energie values redundant if this were to be ignored, as our activation energies are of the same order of energy as this difference in energy of the conformers of the reactant.

First a molecule of 1,5-hexadiene was constructed in Gaussian (app2), with an anti-periplanar arrangement of the central 4 atoms, and its conformation was optimised according to the Hartree-Fock (HF) method using a 3-21G basis set. The basis set works as it takes the co-ordinates of our "guess" structure, and then moves our atoms slightly away from these co-ordinates whilst numerically solving the schrödinger equation, and then giving an energy. If this energy is lower than the original energy of the molecule, then the calculation will move the atoms in this direction on the potential energy surface until it reaches a miniumum on the surface. Later on we will use different methods which are more powerful, but are however more time-consuming. This guess arrangement can be seen below in a Newman projection between C3-C4 below:

As we can see the sterically bulky vinyl groups have a dihedral angle θ = 180° between C3-C4 and so we would expect that this may be a low energy conformer due to the lack of steric repulsion between our groups. For these calculations we have not used the most powerful of basis sets however as we are dealing with a large molecule we must use it as we do the initial calculations so the calculations do not take too much time. This basis set will allow us to compare the conformations and then select the lowest energy conformation for performing further optimisations. The calculation was set up with job type "optimisation" using "HF" method and a "3-21G" basis set, and gave the following results:

Energy: -231.69254 a.u

Symmetry: C_i

The link to the calculation can be found here: File:REAC APP OPT.LOG

We can also check the symmetry by "symmetrizing" our molecule using Gaussian, and then we are given a point group of the molecule, which for this conformer is C_i. Of course we must now run energies of more conformers of 1,5-hexadiene to now compare this value of energy to. The next conformer that was investigated was the Gauche confomer, this is where the central 4 carbon atoms have a dihedral angle θ = 60°, as can be seen below in a Newman projection form below:

We must run the calculation according to the same method and basis set that we used previously otherwise we would be unable to contrast our results. This is beacuse different basis sets start at different points on the potential energy surface, and so they will give different values of the energy depending on which basis set is used. To compare energy values from different basis set calculations would therefore be meaningless. We therefore ran the next conformer again using "optimisation", with method "HF" and basis set "3-21G" which gave the following results:

Energy: -231.68772

Symmetry: C₂

The link to the calculation can be found here: File:REAC GAUCHE OPT.LOG

As we can see we now have a higher energy of the molecule by around 0.01 a.u. One reason for this may be the unfavourable steric clashes of the R groups, however in order to be sure of this we must carry out further calculations. The symmetry of the molecule has now changed also to a point group of C₂, which will be due to a C₂ axis of symmetry which travels through the central carbon atoms C3-C4. As we can see from this conformer though, it is also possible to change the conformation of the molecule whilst keeping this C3-C4 gauche link and so we must see if this will also give us a different energy of the molecule, whether it be higher or lower. The next calculation carried out was a guess at the lowest conformation of 1,5-hexadiene and again was carried out using the same method and basis set as previously employed. This conformer was drawn into Gaussian and gave the following results:

Next conformer: Guess (anti4) Energy: -231.69097

Symmetry: C₁

The link to the calculation can be found here: File:REAC GUESS OPT.LOG

As we can see we now have a lower energy, as we have reverted back to a anti-periplanar linkage between our C3-C4 carbon atoms, although it is higher than the first antiperiplanar structure that was calculated. This may be due to the unfavourable interactions between the vinyl groups which as we can see are now pointing inwards towards each other rather than away from the molecule. The symmetry of this conformation has also changed as we now have C₁ symmetry, meaning that this molecule contains only 1 axis of symmetry equal to a 360° rotation around the z axis, as opposed to the other two conformers we have seen which did have axis of symmetry. We can now use these calculations to perform a more powerful optimisation calculation using a different basis set and thus get a more accurate potential energy minimum of 1,5-hexadiene.

We will now optimise the first anti-periplanar conformation further by using a different basis set. This basis set is now using the so called DFT method (Discrete Fourier Transform) rather than the Hartree-Fock method. The reason for this change is that we can now use a more accurate basis set, 6-31g, and this will give us an energy for the molecule which is more accurate. Using a different basis set means that our calculation will begin at a different point on the potential energy surface and so will give us a different figure as it converges towards the minimum on the potential energy surface. However we now have 6 primitive Guassian functions in the calculation rather than 3 when we used the 3-21g basis set in the Hartree-Fock method. These calculations are more accurate however they are time intensive and so this is the reason we have not used them from the beginning. This conformation gave the following energy under the 6-31g basis set:

Energy: -234.55970 a.u

Symmetry: C_i

The link to the calculation can be found here: File:REAC APP OPT 631G.LOG

As we can see in comparison to the first method we now have the same symmetry (as we would expect considering it is the same conformer as previously),this suggests that the calculations are actually the same. However when we see the energy of the molecule there is a marked difference as we are now at ~-234 a.u rather than ~-231 a.u. As we can see this is by far a trivial amount of energy and so the calculation has given us crucially a lower energy of the conformer and indeed the molecule as a whole. We know that a molecule will always tend towards the minimum of the potential energy surface, and so this calculation is more accurate as it has given a more negative energy than the previous calculation. We know from quantum mechanics that the lowest energy is the energy closest to the true value of the potential energy of the molecule from the variational theorem, which incidentally is the method (the variation principle) used by the Hartree-Fock method to find the potential energy minimum.

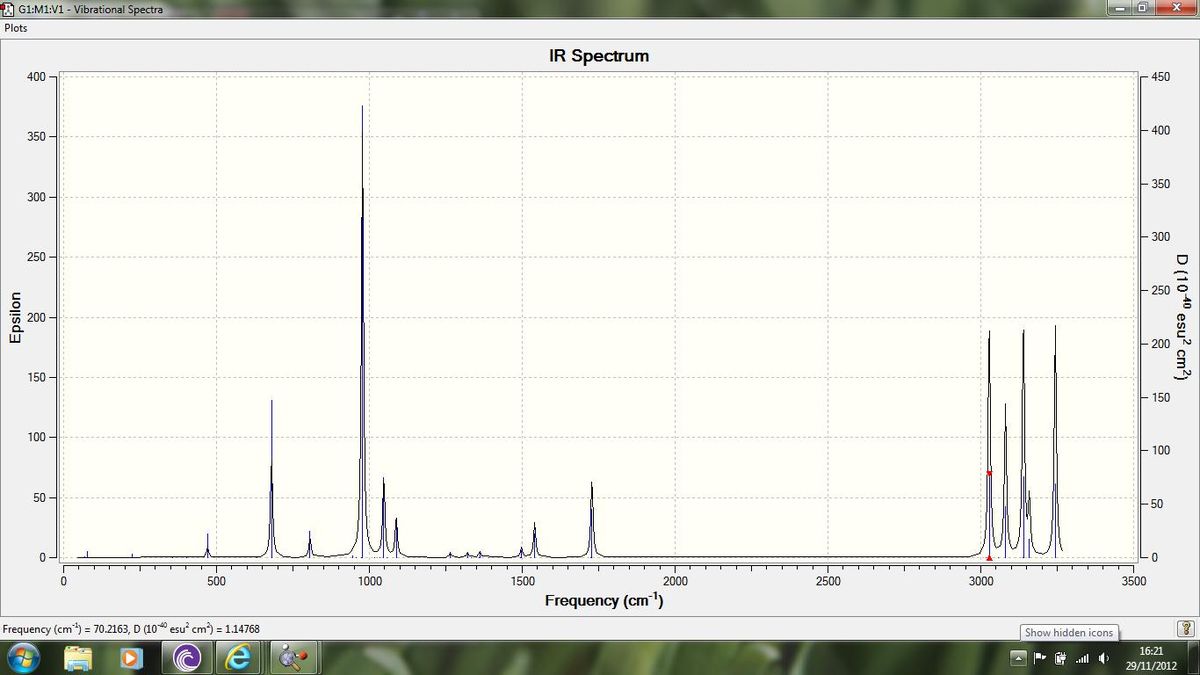
We can now run a frequency analysis also, which will allow us to visualise the vibrations of the molecule and also allow us to predict the gas-phase IR spectrum. This calculation was again run using the DFT method and 6-31g basis set. The IR spectrum as predicted by this calculation is shown in figure 2 below:

Figure 2. Gas-phase IR spectrum of 1,5-hexadiene

Energy: -234.55970 a.u

The link to this calculation can be found here: File:REAC APP FREQ 631G.LOG

The vibrational analysis confirms that there are no vibrational modes which have a frequency of less than 0, these frequencies would show that the optimisation was not complete. We can also see that the energy of the molecule is the same as after the 6-31g optimisation and so we have not changed the molecule in any way through this calculation. With regards to the IR spectrum we can see the peaks in the spectrum that we would expect for the alkene ie. (C=C stretch) - 1728 cm^-1, (C-H stretch) - 3028 cm^-1, (C-H bend) - 1362 cm^-1

The frequency calculation also gives us the following information:

	Sum of electronic and zero-point energy	Sum of electronic and thermal energy	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies
Energy (a.u)	-234.416252	-234.408952	-234.408008	-234.447896

By observing the output file of this calculation we can also discover a variety of thermal chemistry values. The first of these is the sum of the potential energy at 0K and the minimum vibrational energy of the molecule, the output file shows this figure to be -234.416252 a.u. The next value we are given is the value of the energy of the molecule at 298.15K (r.t) and 1 atm, this value of -234.41652 a.u contains contributions from the electronic, rotational, vibrational and translational modes of the molecule and so as we would expect this value is higher than simply than the value at 0K, as at 0K according to the Boltzmann equation only the lowest modes of each parameter are poulated. As we increase the temperature the molecule is able to move to higher states of each parameter and so the potential energy of the molecule can be higher as it can populate higher energetic states of all these parameters. The next term is similar, that of electronic and thermal enthalpies, from the last however it contains a correction for the RT part of the energy, hence why the energy is slightly higher as we now have a positive energy term contributing to this. The last term also includes the entropic contribution to the free energy of 1,5-hexadiene and is lower than all of the other thermochemical values. Now that we have optimised our reactant we must now optimise our two transition states so that we can calculate the difference in energy between them, and thus the activation energy.

Calculating the energy of the "Chair" transition state

The next task is to calculate the energy of the "chair" transition state, in order to do this we must draw a "guess" structure of this transition state into Gaussian and then optimise it to give us the chair conformation of the transtion state. This structure consists of two C₃H₅ allyl fragments which are orientated in the form of a chair conformation with the terminal carbon atoms approx 2.2Å apart as can be seen below:

The first picture shows a Newman projection of this guess structure through C1-C2 and C3-C4, which as we would expect from conformational analysis has all the H atoms in staggered positions with respect to each other. The other picture shows that we have a gap of 2.2Å between our carbon terminal atoms. We must now optimise this transition state. For this we are going to use two different methods, the first of which assumes that we have a reasonable structure for the transition state. We will produce a force constant matrix (Hessian) at the beginning of the optimisation, this will then be updated as the structure converges towards the minimum of the potential energy surface. If this structure is very different from the actual structure then this will not work as the surface of the potential energy surface will be markedly different and so we will get an incorrect structure. The second method will be discussed later.

First we must set up an optimisation for the transition state, to do this we simply perform a optimisation and frequency by selecting the job type as "Opt+Freq" and selecting "Optimisation to a TS(Berny)". Again we will run these calculations using the HF method and a basis set of 3-21G. When we run the calculation we find that by looking at the vibrational modes we can see that we have a "imaginary" mode at -818 cm^-1, as can be seen by clicking the image below this vibration actually corresponds to the cope rearrangement:

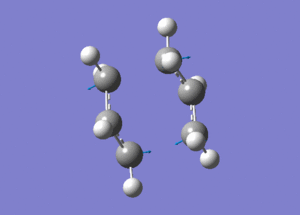
The link to this calculation can be found here: File:CHAIR TS OPT C.LOG

The next method we will use to optimise the transition state is the frozen co-ordinate method, again for comparitive purposes we will use the HF method and a 3-21G basis set. This involves freezing the co-ordinates of the terminal carbon atoms which are going to form/break in the course of the rearrangement, and then optimising the rest of the transition state whilst these are fixed. The calculation was run and gave a result similar to the previous method, but now the distance between the terminal nuclei is fixed to 2.2Å. We now un-freeze the terminal carbons so that they can be optimised, however now we do not calculate the force constants but let the calculation run a normal Hessian, as we are only converging the molecule conformation along one bond. We run a transition state optimisation instead now, so that we will get the potential energy minimum of the entire transition state.

The link to this calculation can be found here: File:CHAIR TS OPT D.LOG

This calculation gives the same conformation as the first method, as we would expect, with the following bond lengths for breaking/making new C-C bonds:

	Optimisation to a TS Bond distance (Å)	Frozen co-ordinate Bond distance (Å)
C-C (forming)	2.21570	2.01984
C-C (breaking)	2.20035	2.01962

As we can see the first method has given us different lengths for the C-C breaking and C-C forming bond lengths, whilst the frozen co-ordinate method has given us essentially the same length. We can also see that these lengths for the frozen co-ordinate method are much shorter than that for the optimisation to a TS method. In this method we first froze the co-ordinates to 2.2Å however we now have optimised the length, the fact that we have split this calculation into two separate components may be what is causing the change in lengths, as the optimisation was done in a single step.

Now that we have our optimised transition state we must find which conformation of 1,5-hexadiene this transition state connects, so that we can calculate the activation energy of the reaction. We cannot predict this conformer, however there is a tool on Gaussian known as the IRC (Intrinsic Reaction Coordinate) which allows us to converge the transition state to a minimum on the potential energy surface and thus give us the final energy of the molecule, and hence the conformer. The IRC works as an optimisation function, by simply following the gradient of the potential energy surface of the molecule down to its lowest point which is our product. First we open up our transition state structure from the previous optimisation (We have decided to use the optimisation from the frozen co-ordinate method) and then set up the job type as "IRC", we can then select a number of different variables for the calculation (again using HF method and 3-21G basis set). The first of these is whether we want to run the convergence forwards from the transition state to the product, backwards from the transition state to the reactant, or in both directions. As our product and reactant are the same molecule this calculation need only be run forwards, as we would get a mirror image of convergence if run in both directions. We can also choose to calculate the force constants always to improve the accuracy of the convergence. The final consideration is the number of points along the IRC that we wish to consider, the more points we use the more accurate the calculation however this is much more time intensive. For this calculation we used 100 steps, and gave the following results:

The above diagram shows how the energy of the molecule changes as we move along the IRC. As we can see as we begin to form the product the energy converges exponetially to the potential energy minimum until it eventually reaches this minimum after 44 iterations. The graph shows a smooth curve as we would expect as we are studying a concerted pericyclic reaction and so there are no intermediates. The energy will simply converge to the minimum, as we can confirm with the graph of RMS gradient v IRC we can see below:

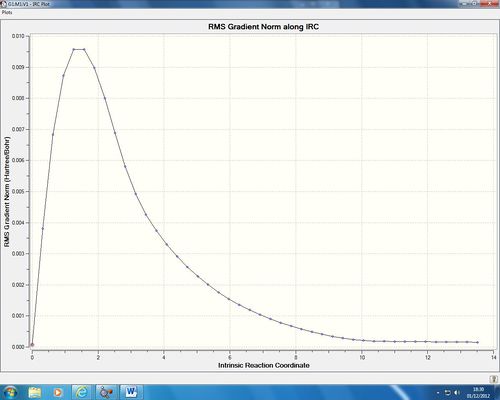
The RMS gradient shows us by how much the energy changes if we slightly move the co-ordinates of the atoms of the molecule. If our calculation has converged to a minimum successfully then this value should be small (<0.001). The graph gives expected results, as it initially rises exponentially as the new C-C bond is formed and then as our molecule falls to the potential energy minima the gradient falls away exponentially to a small value, so that we know that the calculatin has converged successfully.

The link to the calculation can be found here: File:CHAIR TS IRC100.LOG

The video below shows the IRC in progress, as the reaction occurs from the chair transition state to form the new C-C sigma bond, before reaching the minima on the potential energy surface that is 1,5-hexadiene:

The analysis of this information to give the activation energy of the reaction can be founds in the analysis section.

Calculating the energy of the "Boat" transition state

In order to optimise the boat transition strucutre we will invoke a different methodology, that of the QST2 method. In this method we will draw our reactant and product into Gaussian, which can then find our transition state and optimise it for us. Our products and reactant is of course the same molecule, however we must make sure that the atoms are numbered correctly, as during the reaction the sigma bond has rearranged itself as can be seen below:

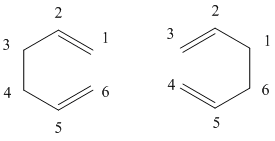
We must therefore change the atom numbers of the reactant and product so that they match this diagram, once this is complete we can now set up the Optimisation calculation. Again we use the job type "Opt+Freq" however instead of selecting "TS (Berny)" we select "TS(QST2)", and then the calculation is run. This calculation fails in fact, and does not lead to the boat transition structure.

The link to the calculation can be found here: File:BOAT TS FAIL.LOG

We must manually modify the structure of the transition state to look like the "boat" structure that we desire, as the calculation does not consider that we can have a boat transition structure. By manually modfying the structure of the transition state Gaussian will be able to find the boat transition structure that we desire. These manual manipulation of the atomic co-ordinates were made to give us the following structures:

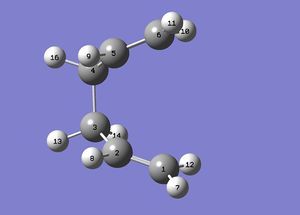
After this manual change in conformation, if we run the job as previously we find that it does converge this time to the boat transition state as we can see below:

The link to this calculation can be found here: File:BOAT TS OPT.LOG

The next task is to now calculate the difference in energy between this transition state and the reactant, as it is this that will give us the activation energy. We can do this by again calculating an IRC from the optimised boat transition structure. This was done using n=100, and gave the following IRC profile:

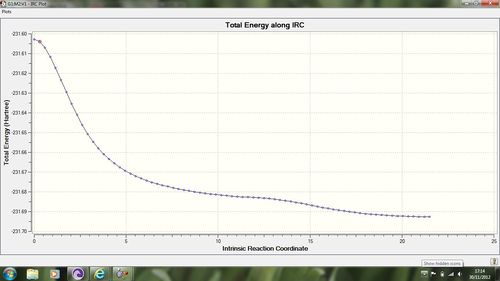
The link to this calculation can be found here: File:BOAT TS IRC 100.LOG

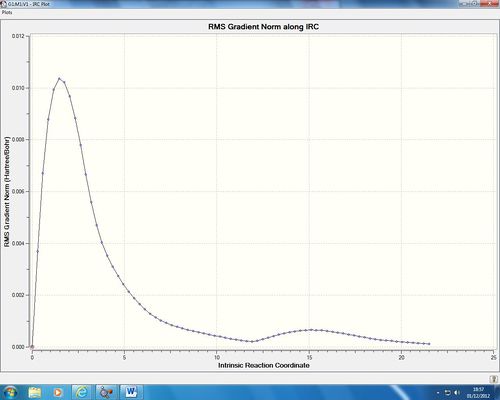
As we can see from the energy diagram this optimisation is not a smooth convergence to the minima, but however contains another maximum before converging to the minima on the potential energy surface. Is this an error? I do not believe so. We can see from Guassian optimisation in figure 5 that the bond forms between carbon atoms 3 and 4 as we converge to point 45 on the diagram. This is the point at which we reach the first minima on the diagram. What appears to happen after this is a configurational reaction, where the reactant is optimised by Gaussian to give us a conformational minimum in energy. One could assume therefore that this is incorrect as we know that the cope rearrangement is a pericyclic reaction and so is concerted. What we have here is an example of an asychronous concerted reaction, where the reaction remains concerted but happens in two different stages. This is easier to visualise from first principle, as of course our new sigma bond must form first before we can rotate around it to give us a conformational minima, the first energy barrier is much bigger than the barrier to rotation, again as we would expect for this system. A video showng the convergence from the transition state to the potential energy minimum, the product, is shown below:

By now calculating the energy difference between the initial transition state and this final conformation we can find the value for the activation energy of this reaction, as can be found in the analysis section below.

Analysis

	HF/3-21G	B3LYP/6-31G	B3LYP/6-31G (0 K)	Experimental (0 K)
ΔE (chair)	45.3	35.0	36.2	33.5 ± 0.5
ΔE (boat)	56.3	41.9	44.0	44.7 ± 2.0

As we can see the prediction made at the beginning of this exercise has proven to be correct, as overall for each basis set and each temperature, the activation energy for the boat transition state is higher than that of the chair transition state. These are in comparison to the experimental values of 33.5 kcal/mol for the chair activation energy and 44.7 kcal/mol for the boat activation energy. As we can see our calculated values are very close to the experimental values and so we can see that the 6-31G basis set is as we predicted very good at predicting experimetal values. We can also see that the activation energies measured at 0K are slightly higher than those recorded at 298.15K (room temperature). This is possibly because at 0K the molecule must be thermally activated so that it has enough energy to react, these differences in energy between room temperature and absolute zero correspond to boltzmanns constant multiplied by temperature (298.15).

One source of error in this calculation is that the calculation of the IRC may not give us the lowest energy conformer of 1,5-hexadiene, and so there will be a small but significant difference in activation energy. However we must remember that at room temperature many of these conformers will in fact be populated as according to the Boltzmann equation, the molecule has kT = ~0.6 kcal mol^-1 thermal energy available to it. This energy is more than enough to overcomethe energetic barrier to rotation and so in fact to determine the populations of the conformers and then calculate the average value of the 1,5-hexadiene molecule would be the most accurate way of determining the average activation energy that we see.

The Diels-Alder Cycloaddition

The Diels-Alder reaction is a [4+2] cycloaddition that was first reported by Otto Diels and Kurt Alder in 1928. This is again another example of a pericyclic reaction which proceeds in a concerted fashion via a cyclic transition state, which we shall attempt to study during this part of the module. Unlike the cope rearrangement that Diels-Alder reaction has found widespread use in organic chemistry, and is arguably the most popular method for synthetic chemists to create a cyclohexene ring. The reaction consists of an electron rich diene and a electron deficient dienophile reacting in a cycloaddition manner. The [4+2] nomenclature refers to the fact that we have 4 electrons from the diene and 2 electrons from the dienophile which come together to form the new ring system. Addition of butadiene to ethylene is the simplest Diels-Alder reaction and occurs via the following mechanism:

It is this reaction that we shall investigate first, the objective being to find and study the transition state and use Molecular Orbital theory to determine why this reaction occurs. Whilst doing these calculations we will no longer be using either the HF or DFT methods, but a semi-empirical method. These are not like ab initio calculations as Gaussian now uses a lot of assumptions when solving the Schrödinger equation as using the full Hartree-Fock method on such large molecules would be too time-consuming. These methods are mainly found in organic chemistry, were they have in fact been found to be very successful.

Diels-Alder reaction of Ethylene and Butadiene

This is the simplest form of the Diels-Alder reaction, a [4+2] cycloaddition of butadiene and ethylene. Butadiene must be in the cis conformation in order for this reaction to proceed, as the trans form would be unable to form a six membered ring due to torsional strain/steric reasons. These two forms of butadiene are both populated and are able to interconvert at room temperature, and so longer reaction times are all that is required for this reaction to proceed at high yield.

First cis-butadiene was modelled in Gaussview, and optimised using the semi-empirical method and a AM1 basis set, this gave the following results:

Energy: 0.04879743 a.u

Symmetry: C_2v

The link to this calculation can be found here: File:AM CISBUTADIENE OPT.LOG

From the mechanism of this reaction and MO theory we know that it is the π orbitals of our cis-butadiene system which will be directly involved in the reaction, and so in order to see whether this reaction is allowed by the Woodward-Hoffman rules we must investigate the properties of the HOMO and LUMO of cisbutadiene with respect to the internal plane of symmetry as can be seen below:

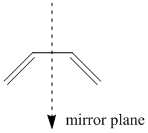
Cisbutadiene has an internal σ_v plane of symmetry, meaning that it is vertical, what we must now deduce is whether the HOMO and LUMO (the orbitals involved in creating our two new σ bonds are symmetric or asymmetric with respect to this internal plane of symmetry. Below we have the HOMO for cisbutadiene:

We can clearly see that with respect to the plane of symmetry this molecular orbital is antisymmetric, as the sign of the wavefunction changes as we cross the mirror plane (ie. colour changes from red to green). We therefore give this molecular orbital the designation a. Below is the LUMO for cisbutadiene:

Unlike the HOMO this molecular orbital is now symmetric with respect to the mirror plane (the sign of the wavefunction stays the same with reflection in the mirror plane), and so we denote this orbital s. This now gives us an energy profile diagram which looks like this:

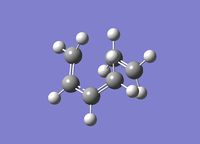
The transition state for this reaction was then studied. This involves approach of the ethylene above the cisbutadiene, thus allowing maximum orbital overlap in order to create our new σ bonds. This can be seen below:

We can see that the butadiene approaches the ethylene at an angle of 100°, we can see that the partially formed sigma bonds in this structure have bond lengths of 2.12Å, this compared with a typical C-C sp³ bond length of 1.53Å and sp² bond length of 1.34Å, whilst the Van der Waals radii of a Carbon atom is 1.70Å. Multiplying the value of the Van der Waals radius by 2 gives a value of 3.40Å, and so we can see that as the partially formed bond length falls within this range this shows that we have significant orbital overlap from the terminal carbons. However as this is a maximum in energy we would expect this not to be at the ideal 1.53Å of an sp³ bond length.

The correlation diagram shows what happens to our HOMO and LUMO MO's as we move from the reactants to products, the HOMO of butadiene decreases in energy, whilst the LUMO increases in energy, the ethylene π orbital remains the same. From this daigram we can use the Woodward-Hoffman rules to show that this reaction is allowed. As we can see in the diagram the movement from reactant to product hs not broken the symmetry through the mirror plane (the orbitals still have the same symmetry), and so this means that this reaction is allowed.

In order to optimise the transition state it was decided to use the frozen co-ordinate method. This is as before were we freeze the co-ordinates of the atoms which will form our new bonds, optimise the rest of the system to a minimum, then un-freeze the atoms and optimise the entire system to a transition state (berny). This was done as before and gave the following results:

The link to the calculation can be found here: File:BUTADIENE TS OPTNEW.LOG

By performing a vibrational analysis we can determine if we have a transition state. As in the cope rearrangement if we have a transition state we should have an imaginary (negative) vibrational mode, which when animated should correspond to the formation of the product. As we can see below this is what we find:

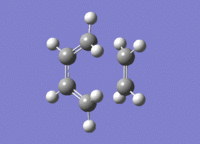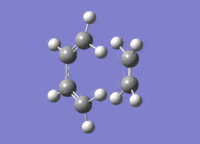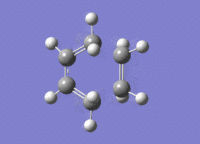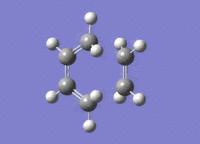
A link to the calculation can be found here: File:BUTADIENE TS FREQ.LOG

The negative frequency confirms that we have found the top of a trough of a potential energy surface, as when this is differentiated twice we get a negative value meaning we have found a maximum of the energy. All of the positive frequencies correspond to minimum in potential energy. We can now run an IRC calculation on the molecule to see how the molecule converges down the potential energy surface to the product. This was done as in the cope rearrangement in the backwards direction, using 100 iterations. This was done, and a video of the convergence is shown below:

A link to the calculation can be found here: File:BUTADIENE TS IRC.LOG

We can see from the animation that the formation of the two new sigma bonds is synchronous, as opposed to the cope rearrangement which we observed to be a concerted but ascynchrnous reaction. The lowest positive frequency that we observe is one which breaks the symmetry of the molecule as it is the highest energy miniumum on the potential energy surface. The IRC for this reaction can be seen below. This is a graph plotting the potential energy of the system as it converges from the transition state to the product. This was run in the backward direction from transition state to products only, calculating the force constants always and using n = 100 iterations:

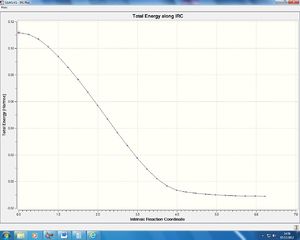
The transition state as expected is at the highest potential energy on the graph and the product is at the lowest potential energy. A smooth sigmoid curve can be observed between these two points as the product begins to form and then drops exponentially to the minima on the potential energy surface.

As we would expect the butadiene approaches at an angle that produces maximum orbital overlap between the HOMO of butadiene and the LUMO of ethylene. As the LUMO of ethylene is populated the π bond of ethylene is broken as we observe, and then the 2 new sigma bonds are formed between the butadiene and ethylene before the molecule reaches an optimum conformation. Again we inspect the symmetry properties of the HOMO and LUMO of the transition state. The HOMO is drawn below:

We can see that as in cisbutadiene the HOMO is anti-symmetric with respect to the internal plane of symmetry, there is significant orbital overlap between the two systems as we can see between them. This overlap is what causes te sigma bonds to form between the carbon atoms. The LUMO of the transition state is shown below:

This molecular orbital is symmetric with respect to the mirror plane, again like cisbutadiene the LUMO's are of the same symmetry. What can we conclude from this? The reaction occurs beacuse we have the HOMO of butadiene (a) and the LUMO of ethylene (a) interacting, it is essential that these orbitals be of the same symmetry as we saw in the correlation diagram. As we can see in the transition state the fact that these orbitals are of the same symmetry allows for maximum bonding interactions between the two reactants, and it is this which causes the new bonds to form. The fact that the HOMO of the transition state is asymmetric about the mirror plane proves that the reation has proceeded conserving the symmetry showing that the reaction is allowed according to the Woodward-Hoffman rules. One might assume that the reaction could also occur in the opposite fashion, using the HOMO of ethylene and the LUMO of butadiene. This in fact can and does occur, as both of these orbitals are symmetric with respect to the plane and produce a MO of the same symmetry.

Diels Alder reaction of Cyclohexa-1,3-diene and Maleic Anydride (Exo product)

This Diels-Alder reaction is of more interest than the previous system, as now we have substituents on our diene and the dienophile. Another consideration we must make is the stereochemistry of the product, as this reaction can in fact give two diastereoisomers as shown below:

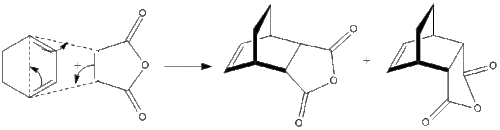
As we can see the reaction gives us a mixture of diastereoisomers, the exo form on the left, and the endo form on the right. The stereoselectivity of the reaction depends on the conditions we employ. It has been shown that the kinetically favoured endo product is formed at lower temperatures as it has a lower activation energy to reaction. The exo form is the thermodynamically favoured product, and if the reaction is left for a long time the endo product will undergo a retro Diels-Alder reaction and equilibrate to the exo product. This is summarised in the potential energy diagram below:

The reactants sit in the middle and can travel one of two ways along the potential energy surface. If they move to the right we have a small activation barrier to reaction but a less thermodynamically favoured product which is the endo isomer. If we move to the left we have a larger barrier to reaction but we produce the more thermodynamically favoured product the exo isomer. Why is the product more favoured thermodynamically? This is what we shall discover as we carry out these calculations.

First of all, maleic anhydride and cyclohexa-1,3-diene were optimised in Gaussian using the semi-emprical method and an AM1 basis set, this gave the following results:

Energy: 0.0277128 a.u Energy: 0.00002775 a.u

The links to these calculations can be found here: File:MALEIC OPT.LOG/File:CYCLOHEXADIENE OPT.LOG

These optimised reactants were then placed in a new window in Gaussian in order to perform the optimisation. Again the frozen co-ordinate method was used, with the same procedure as described previously. The carbon atoms forming the new sigma bonds were frozen, the rest of the molecule was optimised. These atoms were then unfrozen and a optimisation calculation to a transition state(berny) was performed. This gave the following structure:

The link to this calculation can be found here: File:MALEICADDUCT OPT EXONEW.LOG

Again by performing a frequency analysis we can confirm that we have found a maximum in the potential energy surface and hence the transition state. A frequency analysis was carried out and a negative frequency at -811 cm^-1 was found, which corresponds to the following vibration:

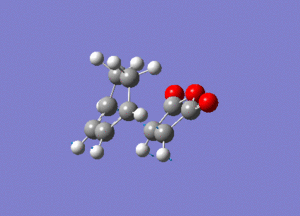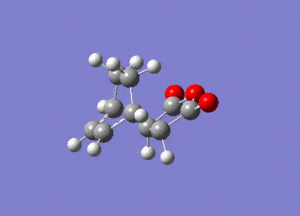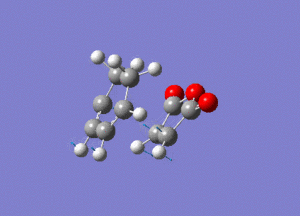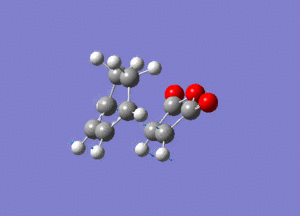
The link to this calculation can be found here: File:MALEICADDUCT FREQ EXO.LOG

As we can see this vibration corresponds to the formation of the Diels-Alder adduct, and so we can see that we have found the transition state for this reaction. In order to deduce the energies of the transition state with respect to the product, we must run an IRC calculation as previously. However on this occasion as the product and reactant are distinctly different it was decided to run the IRC in two separate procedures. The first procedure was run in the "backwards" direction and corresponds to the molecule moving back down the potential energy surface to the reactants. As before this was run calculating the force constants always and using n = 100 iterations. This gave the following animation:

The link to this calculation can be found here: File:MALEICADDUCT IRC EXONEWBACKWARD.LOG

As we expect the molecules fall away and form the reactants as they move away from each other. Other information from this calculation include the IRC v potential energy graph as we move along the IRC, and this can be seen below:

Again as expected the potential energy falls from the maximum at the transition state down to the energy of the reactants which is much lower. We can now run the IRC in the forwards direction, in order to observe the formation of the product from the transition state. This was done according to the same parameters and gave the following animation:

The link to this calculation can be found here: File:MALEICADDUCT IRC EXONEWFORWARD.LOG

As we can see our molecules move closer together and the C-C π bond in the maleic anhydride is broken. This as the HOMO of the cyclohexa-1.3-diene begins to populate the LUMO of the maleic anhydride thus filling an anti-bonding molecular orbital and breaking the bond. We then have formation of the two new sigma bonds and then the molecule rotates to form a conformationally energetically favourable state. The IRC gives us an insight to the potential energy as the molecules converge from the transition state to the product:

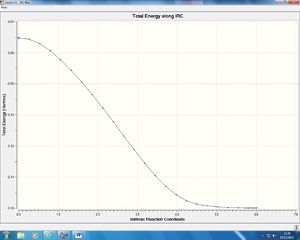
The potential energy falls away exponentially as we move from the transition state to the product. The energetics of this transition and the two IRC graphs are discussed in more detail in the analysis section. What we can now do is plot the Molecular orbitals of the transition state so that we can compare them with the molecular orbitals of the endo transition state and find a reason why the exo product is thermodynamically favoured. As with the reaction of ethylene and butadiene we must find a mirror plane in the reactants that we can then compare our molecular orbitals to, to determine whether they are symmetric or asymmetric and hence whether the reaction is allowed. One mirror plane that exist in the reactants is shown below:

If we now reference all of the molecular orbitals to this internal mirror plane we have a sound basis on which to perform an MO analysis. From an MO analysis we can see that the HOMO and LUMO of the transition state look like the following:

HOMO

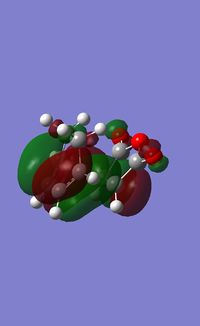
LUMO

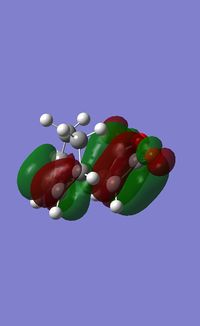
If we take into account this plane of symmetry we can see that the HOMO is a symmetric with resppect to the mirror plane and the LUMO is symmetric with respect to the mirror plane. What we must now do is calculate the transition state of the endo product so that we can compare our two structures.

Diels Alder reaction of Cyclohexa-1,3-diene and Maleic Anydride (Endo product)

In order to quantify the data that we have already gained from the exo product calculations we must now calculate the properties of the endo product. All of the following calculations were done using a semi-empirical method and an AM1 basis set. The endo product is where the maleic anhydride faces down with respect to the rest of the system, rather than in the exo form where it is facing up. Again the optimised cyclohexa-1,3-diene and maleic anyhdride that were used previously were used again, and on this occasion the maleic fragment was rotated through an angle of 180° so that the endo product would be formed (this is discussed in more detail in the analysis section). The frozen co-odinate method was again employed and gave the following transition state structure:

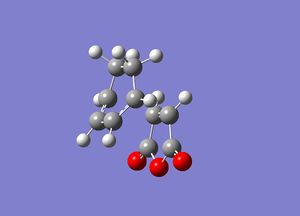
The link to this calculation can be found here: File:MALEICADDUCT OPT ENDONEW2.LOG

As you can see this is very similar to the structure we found earlier for the exo transition state, except now the maleic anhydride fragment is pointing down rather than up. By performing a frequency analysis it was found that a negative frequency existed at -806 cm^-1, this frequency is shown below:

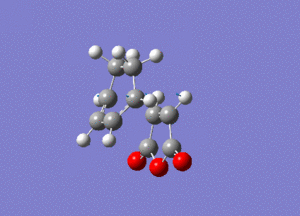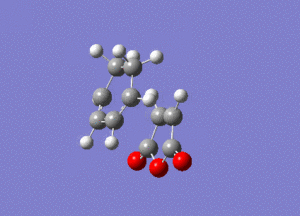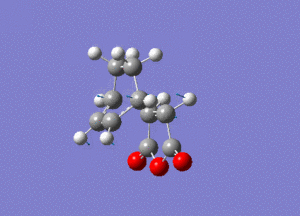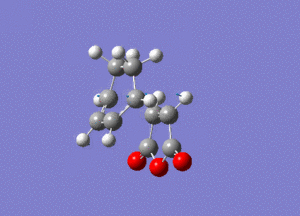
The link to this calculation can be found here: File:MALEICADDUCT FREQ ENDO.LOG

The frequency corresponds to the formation of the Diels-Alder adduct and as it is negative we can confirm that we have found a maximum in the potential energy surface and hence the transition state for this reaction. An IRC was then run so that we can find out more about the convergence to the minimum of the potential energy surface, and hence how the energy of the system changes as we converge to the products. The IRC was performed in both directions, calculating the force constants always and using n = 100 iterations. This was run and gave the animation we see below:

The link to this calculation can be found here: File:MALEICADDUCT IRC ENDONEW.LOG

As we see the reactnats come together, form the transition state and then the product. The transition state leads as in the exo formation to the breaking of the C-C π bond before we then have formation of the two new sigma bonds. The product then reahces its most energetically favourable state as we have reached the minimum of the potential energy surface. This is conformed by the IRC that was then calculated:

The potential energy starts with the reactants, rises slowly as it reaches a maximum at the transition state, and then decays exponentially as we reach the products, which are lower in energy than the reactants. This graph suggests that we have a late transition state as the transition state maximum is closer to the products than it is to the reactants. If we now perform an MO analysis on the transition state we find that the HOMO and LUMO look as follows:

HOMO

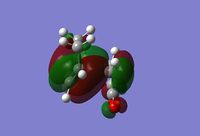
LUMO

An in-depth analysis of these orbitals is provided in the analysis section.

Analysis

We can see from the potential energy diagram earlier that the activation energy for the formation of the endo product was lower than the acitvation energy for the exo product, meaning that the endo product is kinetically favourable. One way of explaining this is to look and compare the transition structures for each product:

Endo Transition state

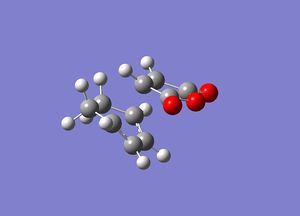
Exo transition state

We can see from these images that in the endo transition state the maleic anhydride fragment is pointing away from the ring system, whilst in the exo transition state it is pointing directly over it. Thus the reason for the energy of the exo being higher is simply steric repulsion, this transition state is more sterically strained than its endo counterpart, and so it wont be as easily formed and is higher in energy. We can confirm this by using our IRC calculations to calculate the activation energy for each reaction. As in the cope rearrangement because we are studying a pericyclic reaction and the reaction is therefore concerted, we can calculate the activation energy by simply subtracting the energy of the reactants from the energy of the transition state. This gives the following values:

Activation energy (Endo, 298.15K): 0.04250841 a.u = 26.7 kcal/mol

Activation energy (Exo, 298.15K): 0.04495197 a.u = 28.2 kcal/mol

As expected we have a lower barrier to the transition state for the endo product rather than the exo product. Another reason that the exo form may be more strained is due to the strain between the Carbons of the maleic anhydride and the terminal Carbons of the cyclohexa-1,3-diene. In the endo structure as the maelic fragment is facing down this means that the oxygen atoms are pointing away from the rest of the cycli structure, whilst in the exo form we have the oxygen atoms having axial interactions with the CH₂-CH₂ fragment, this is an unfavourable interaction and so will lead to an increase in potential energy.

Having run MO analyses for each of the products we are now able to conclude why the endo form is kinetically more stable than the exo form. From first principles we can deduce that if the endo transition structure is more stable than the exo transition structure then there must be a stabling interaction present which is not present in the exo transition structure. This is a so called secondary orbital overlap effect, and the lowering of the energy comes from the stabilisation provided from the Oxygen atoms. One may then ask why is this interaction not present in the exo form? The answer to this is that the oxygen atoms are not in the correct orientation in this form to cause such an interaction. Oxygen as we know is a very electronegative element and so its LUMO will be very low in energy and able to accept electron density and thus if it is in the correct orientation it will be able to interact with the dienophile and lower its energy. This means that it will be a lower energy barrier to overcome when the HOMO of the diene interacts with the LUMO of the dienophile and so the energy barrier to reaction will be smaller. By observing the HOMO of each transition structure we will be able to see where these differences lie:

Exo transition structure HOMO = -0.34274 a.u

Endo transition structure HOMO = -0.34505 a.u

The energy difference is small but we can see that the endo HOMO is defintely lower in energy than the exo HOMO. We can see that in the endo transition state the p orbitals on the oxygen atoms are aligned correctly in order to overlap with the diene system, whilst in the LUMO this is not the case. Another factor we can see is that in the endo structure there is electron density on the central O atom of the maleic fragment whilst in the exo structure there is no electron density on the O. Electron density on this O atom will lower the energy of the HOMO as O is electronegative and so its atomic orbtials are lower in energy. It is this stabilising effect which causes the endo transition state to be lower in energy than the exo transition structure, although in order to prove this rather than speculate, one would have to solve the Salem-Klopman equation in order to calculate this difference in contribution.

One factor that has been neglected in all of these transition state calculations is that the reactants can polymerise and react with themselves.

Conclusion

In conclusion we have seen that computational methods can be used to model molecular systems including optimising molecules, performing frequency analysis to find vibrational modes, and also finding transition structures. Once we find the transition structures we can then calculate IRC for reactions to see how they proceed. A variety of methods have been used in these calculations, from DFT and HF for the cope rearrnagement, to semi-empirical for the Diels-Alder reaction. The values that have been calculated for the Diels-Alder reactions are not as accurate as the other methods (for reasons already discussed) and so whilst we can successfully perform comparisons of energy between these calculations, the method employed means that we cannot use these values for energy when comparing against experimental data as they just arent accurate enough. In order to investigate the Diels-Alder reaction and the secondary orbital overlap effect further it would be beneficial to calculate the Natural Bond orbitals and use these to solve the Salem-Klopman equation, however unfortunately this is outside the scope of this laboratory. Computational methods can be used to complement experiments performed in the wet laboratory, and whilst there are many approximations that are used, we have seen that some of the methods used in particular DFT, can give results which are in very good agreement with experiment.