Rep:Mod:am1613

Transition States

Introduction

In this experiment the transition states of the Cope Rearrangement and the Diels-Alder reaction were studied in order to determine the most likely reaction path. To do so GaussView was used the the structures were optimised to different levels of theory, using different methods.

The methods used are the following:

• Hartree-Fock: It's an approximation method to determine the wave function and the energy of a system in a stationary state. It assumes that the wave-function of that system can be approximated by a Slater determinant, ignoring Coloumbic interactions. Slater determinants are solutions to antisymmetrical wavefunctions with more than two electrons.

Nf710 (talk) 19:30, 10 February 2016 (UTC)This is only true for electrons of the same spin in their same spin orbitals each of the electrons feels a mean field potential.

• DFT: The Density Functional Theory (DFT) is more accurate than the HF method as it takes into account the electronic interactions between the electrons (i.e. it doesn't ignore Coloumbic interactions). It investigates the properties of a many-electron system using functionals (a function of a function).
• Semi-empirical: This method allows the study of larger molecules by involving integral approximation and parameterisations that limit its accuracy, it introduces drastic approximations to speed up the calculations. To compensate for these, empirical parameters are incorporated and the data is compared to empirical or theoretical reference data and calibrated.

3-21G is the minimum basis set used in this experiment. The 6-31G* basis set was also used, which adds polarisation making the calculated energies are more accurate.

All the structures were optimised to either a minimum (conformation with the lowest energy) or a transition state (energy maxima), depending on what was being optimised. For the transition state, the molecule could be optimised to a TS Berny, QST2 or QST3:

• TS(Berny): relies upon a 'guess' structure that is optimised to a transition state and then an IRC is computed to confirm the transition state has been reached (i.e. there is a maximum on the potential energy surface). Nf710 (talk) 19:34, 10 February 2016 (UTC) Do you not mean a second derivative

• QST2 and QST3: these methods perform optimizations by default using redundant internal coordinates. They will converge efficiently to the actual transition structure using an empirical estimate of the Hessian and suitable starting structures. They don't rely on a 'guess' transition state structure, instead the reactant and product structures are the input.

All the reactions studied in this experiment are concerted and go through a cyclic transition state, i.e. they are pericyclic reactions. When such reactions are thermally controlled, the Woodward-Hoffman rule can be used to predict the stereoselectivity and whether the reaction is allowed or not. The Woodward-Hoffman rule states the following:

$\sum (4q+2{)}_s+(4r{)}_a=ODD$

Where q and r are integers. s and a correspond to suprafacial - only one face is involved in the formation of the bond - and antarafacial - opposite faces are involved in the bond formation.

However, this rule cannot provide quantitative analysis of how the geometries and energies of the molecules change as the reaction takes place. Thus, we need computational methods to solve the Schrodinger equation of many electron systems.

The Cope Rearrangement

The Cope rearrangement is an organic reaction that involves a [3,3]-sigmatropic rearrangement of 1,5-dienes. There'a been a lot of controversy regarding the mechanism of this reaction. Now, it's widely accepted that it is a concerted and pericyclic rearrangement that goes via a chair or boat transition state. The objectives of this section are to locate the low-energy minima and transition structures, to determine the preferred reaction mechanism.

Nf710 (talk) 19:36, 10 February 2016 (UTC) this is a good general inreoduction however you could have gone into more detail about the various methods employed

Cope Rearrangement

Optimising the Reactants and Products

Both the reactant and the product are 1,5-hexadiene, which can adopt different conformations as the dihedral angle changes due to the free rotation around the C3-C4 bond . The dihedral angle for the anti conformer was set to 180˚ and for the gauche conformer to 60˚. The following structures were modelled and optimised at the HF/3-21G level of theory to obtain the point group and energy.

Conformer	Structure	Point Group	Energy/Hartrees	Relative Energy/kcal/mol
Anti1	caption	C2	-231.69260235	0.04
Gauche2	caption	Ci	-231.69166702	0.61

The energy of the anti1 conformer is lower than that of the gauche2 conformer. This is what I would have expected due to the increased steric hindrance in the gauche conformation. However, the gauche3 conformer is the one with the lowest energy according to Appendix1. This could be due to the favourable interaction between the π electrons of the carbon-carbon double bond and the nearby vinyl proton.

~~~~ You could have shown the favourable pi overlap with the orbitals from the .chk file.

Then, the anti2 conformer was also modelled and optimised at the HF/3-21G level of theory. For this conformer, the energy given in the Appendix is of -231.69254. After optimising the molecule, an energy of -231.69253528 was obtained, which is really similar to the given value.

The conformer was then reoptimised at the B3LYP/6-31G* level, which uses less approximations. Hence, the generated conformation is more accurate than the previous one. However, as can be seen below, the difference in the bond lengths and bond angles is really minor.

Geometries with Different Optimisation Methods

	Atoms	HF/3-21G	B3LYP/6-31G*	Labelled Structure
Bond	C1-C4 and C14-C12	1.31613	1.33350
	C4-C6 and C9-C12	1.50891	1.50720
	C6-C9	1.55274	1.55506
Angle	C1-C4-C6 and C9-C12-C14	124.810	125.221
	C4-C6-C9 and C6-C9-C12	111.347	112.657

After running a frequency calculation, it was seen that none of the vibrational modes of the anti2 conformation were imaginary (i.e. all the frequencies were positive). Also, the IR spectrum was plotted. It shows the expected shifts for 1,5-hexadiene: a =C-H stretch at 3150 cm-1 and =C-H bending at 950 cm-1 to indicate an alkene, it also shows a C-H stretch at 3025cm^-1 and C-H bend at 1480 cm^-1 to indicate the alkane linker.

caption

caption

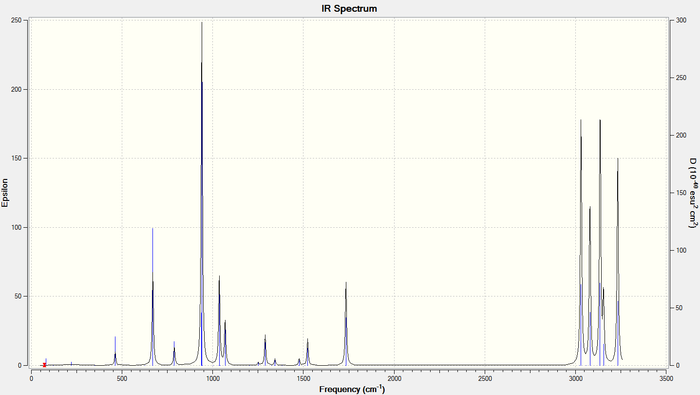
The following thermochemistry data was extracted:

caption

Optimizing the "Chair" and "Boat" Transition Structures

The Chair Structure

As previously mentioned, the Cope rearrangement can go via a boat or a chair-like transition state. Both of these transition states were modelled and studied. First, an allyl fragment was drawn and optimised at the HF/3-21G level. Two optimised fragments were then orientated in such way that the two terminal ends were about 2.2Å from each other in a "guess" chair transition structure. This structure was then optimised in two different ways.

Guessing Method

The first method used is the Guessing Method, which computed the force constant at the beginning of the calculation. The guess structure undergoes an optimisation to a TS(Berny) with the force constant calculated once. The key words "Opt=NoEigen" were added when running the calculation in order to prevent it from crashing if more than two or more imaginary (negative) frequencies were detected. After running the calculation, only one negative frequency was obtained at -817.85cm^-1. Therefore, there is only one transition state which confirms that the Cope rearrangement is a concerted process.The reason why transition states have an imaginary frequency is that they have a negative force constant, k, (i.e. a maximum on the potential energy surface) and so according to Equation 1, they must have an imaginary frequency (the square root of a negative number doesn't exist).

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$ (Equation 1)

Negative Frequency

Freeze Coordinate Method

The other method used is the Freeze Coordinate Method. The distance between the two terminal carbons of the allyl fragments were frozen and fixed to 2.2Å. This is done in order to eliminate some degrees of freedom and therefore fix the molecule in the chair position whilst the optimisation takes place. The molecule was then optimised to a minimum at the HF/3-21G level. Once the optimisation was completed, the frozen bonds were relaxed again and optimised to a TS(Berny) at the HF/3-21G basis set. As when using the Guessing Method, an imaginary frequency was obtained at -817.85cm^-1 due to the same reason previously explained.

The two optimised structures obtained with the two different methods were then compared and it can be seen that there is no significant difference and that therefore, both methods can be used indifferently.

	Atoms	Guess Method	Freeze Coordinate Method	GaussView Structure of the Chair Transition State
Bonds	C1-C2 and C9-C10	1.38927	1.38932
	C2-C3 and C10-C11	1.38923	1.38922
	C3-C11	2.02047	2.02062
Angles	C11-C10-C9 and C3-C2-C1	120.504	120.526
	C10-C9-C1 and C2-C3-C11	101.854	101.851

The Boat Structure

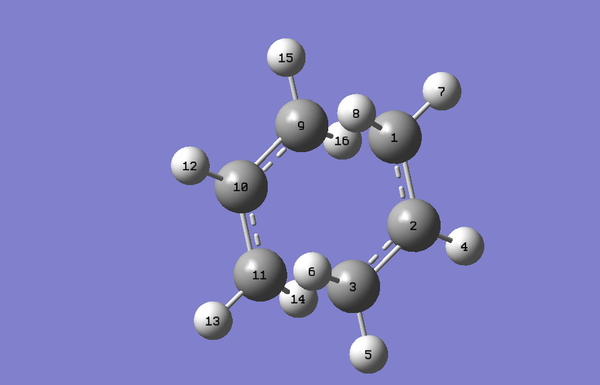
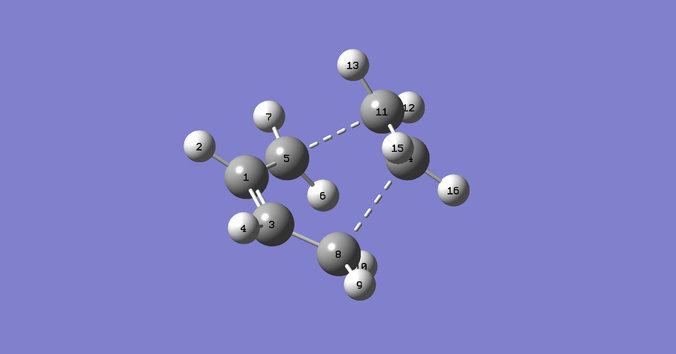
To optimise the Boat Transition State the SQT2 method was used, which requires us to model the starting material and the product in the same molecule group. The program then automatically calculates the transition state. However, for this to work the atoms of the reactant and the product need to be correctly numbered, as if the rearrangement had occurred:

caption

The first time the calculation was run, it failed. This was because it failed to rotate around the central bond and therefore a wrong transition structure was obtained. To correct that, the dihedral angle of both the product (C4-C1-C14-C12) and the reactant (C4-C6-C9-C12) was changed to 0˚ and the inside angle of the reactant (C4-C6-C9 and C12-C9-C6) and product (C12-C14-C1 and C4-C1-C14) was changed to 60˚, to give the following geometries:

caption

The QST2 calculation was run for the second time, which converged to the boat transition structure and gave one imaginary frequency at -839.86cm-¹, as expected:

Nf710 (talk) 19:41, 10 February 2016 (UTC) Correct frequcies and energies

Intrinsic Reaction Coordinate

The Intrinsic Reaction Coordinate Method, or IRC method, allows us to follow the path of the potential energy connecting the reactants, transition states and products. The kinetic energy is constrained to zero at any point along the path. This method is needed as it is not possible to predict which conformer will lead to which path just by observation.

Due to the reaction being symmetric, the calculation was set to run only in the forward direction. It was also set to always calculate the force constant and to find 50 points along the IRC. Since only 44 points were found, it was concluded that the lowest energy configuration was found (i.e. the 44th structure) which, as can be seen on the IRC plot, corresponds to a minima and it shows that the energy has converged.

caption

caption

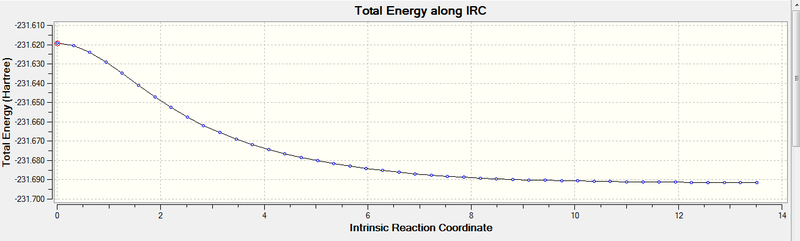
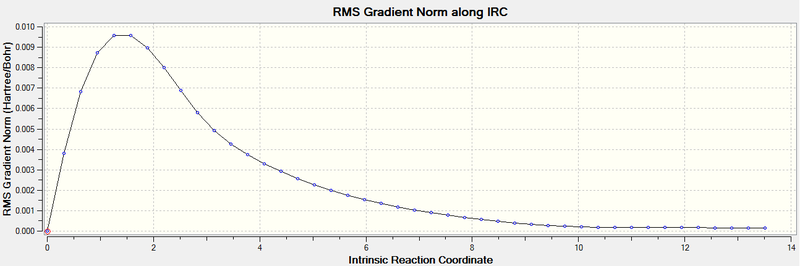
The 44th geometry was then optimised to a minimum, which confirmed that it was the transition structure. This optimisation gave the same structure, as seen below, and similar energies. When comparing these two structures to the ones in the Appendix1, it can be seen that they correspond to the 'gauche2' conformer and, in fact, they have very similar energies.

44th structure		Re-optimised to a minimum
Geometry	Energy/Hartree	Geometry	Energy/Hartree
	-231.69159008		-231.691667

Activation Energies

Finally, the activation energies of both the boat TS and the chair TS were calculated. This was done by taking the structure previously optimised to a HF/3-21G level and re-optimising it to a DFT B3LYP/6-31G* level of theory. After inspecting the log files of the reoptimised structures it was concluded that the energy had converged and that therefore comparison of the energies of the TS and reactants was possible.

A comparison of the geometries of the reactants and the TS in both levels of optimisation can be found below.

Chair Transition Structure Labelled	Anti2 Labelled	Boat Transition Structure Labelled

Summary of Bond Lengths at Different Levels of Theory

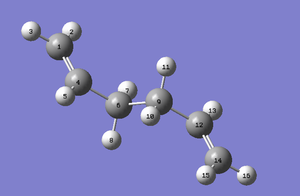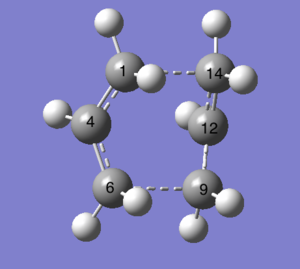Bond	Anti2 HF/3-21G	Anti2 B3LYP/6-31G*	Chair HF/3-21G	Chair B3LYP/6-31G*	Boat HF/3-21G	Boat B3LYP/6-31G*
C1-C4 and C12-C14	1.31613	1.333724	1.38930	1.40765	1.38141	1.39325
C4-C6 and C9-C12	1.50891	1.50620	1.38925	1.40762	1.38138	1.39326
C6-C9	1.55275	1.54506	2.02041	1.96676	2.14041	2.20677
C6-C1			2.02054	1.96690	2.14034	2.20682

Summary of Angles at Different Level of Theory

Angle	Anti2 HF/3-21G	Anti2 B3LYP/6-31G*	Chair HF/3-21G	Chair B3LYP/6-31G*	Boat HF/3-21G	Boat B3LYP/6-31G*
C1-C4-C5 and C9-C12-C14	124.806	125.286	120.504	119.928	121.701	122.241
C6-C9-C12 and C14-C1-C4	111.349	112.657	101.856	103.662	103.386	103.475

As it can be seen, when optimising the structures to a higher level of theory, the variation in the geometry is really small and not significant enough to be important.

However, when comparing the energies for the two different levels of optimisation, it was found that the energy difference was actually bigger and significant. Therefore, it is important to optimise the structures to the higher level of theory HF/6-31G*.

Summary of Energies at Different Levels of Theory

Structure	Electronic Energy/Hartree		Electronic and Zero Point Energy (0 K) / Hartree		Electronic and Thermal Energy (298.15 K) / Hartree
	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
Anti2	-231.69253528	-234.61171063	-231.539539	-234.469219	-231.532565	-234.461869
Chair TS	-231.61932235	-234.55702997	-231.466701	-234.414909	-231.461342	-234.407231
Boat TS	-231.60280216	-234.54296682	-231.451831	-234.403930	-231.445298	-234.395514

To find the activation energies, the energy of the reactant (anti2) was subtracted from that of the transition state, either chair or boat, and then converted to kcal/mol^-1 by multiplying by 627.509. As can be seen in the table below, there's a significant difference between the activation energy of the Chair TS and the Boat TS. The former being the lowest energy path and therefore the most favourable.

Activation Energies /kcalmol^-1

Structure	HF/3-21G (0 K)	HF/3-21G (298.15 K)	B3LYP/6-31G* (0 K)	B3LYP/6-31G* (298.15 K)	Experimental (0 K)
Chair	45.706	44.693	34.080	33.162	33.5 ± 0.5
Boat	55.037	54.760	40.969	40.638	44.7 ± 2.0

Nf710 (talk) 19:49, 10 February 2016 (UTC) this was a good result but your energies were very slightly out in their electronic energy. But your have shown an adequate understanding of the theory and done everything at was asked of you in the first part.

The Diels-Alder Reaction

Introduction

The Diels-Alder reaction is a [4+2] cycloaddition between a conjugated cis diene and a dienophile, which gives a cyclohexane by breaking 3 $\pi$bonds and 1 $\sigma$bonds and forming 1 $\pi$ and 2 $\sigma$. It proceeds through a suprafacial-suprafacial interaction of a 4π electron system of the diene with the 2π electron system of the dienophile. Such interaction is thermally allowed by the Woodward-Hoffman rules (4n+2 cycloaddition).

The reaction is strongly dictated by HOMO/LUMO interaction. The biggest overlap will happen when the dienophile is electron poor (i.e. has electron withdrawing substituents) and the diene is electron rich (i.e. has electron donating substituents). When this is the case, we will have Normal Electron Demand giving rise to a facile reaction. When the dienophile is electron rich and the diene electron poor, we will have a case of Inverse Electron Demand which gives rise to a less facile reaction.

An IRC was computed to confirm that a transition state had been reached.

Ethylene and cis-Butadiene

The mechanism taking place is as follows:

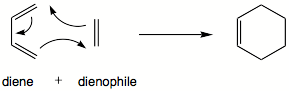
Both the ethylene and the cis-butadiene were modelled on GaussView and then optimised using the AM1 semi-empirical method in order to obtain the MOs. The HOMO and LUMO of cis-butadiene and ethylene can be seen below and upon examination it can be seen that, for the cis-butadiene, the HOMO is anti-symmetric with respect to the plane whilst the LUMO has a plane of symmetry perpendicular to the C3-C2 bond.

Cis-Butadiene
Optimised Structure	HOMO	LUMO

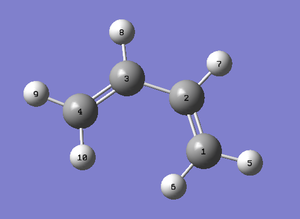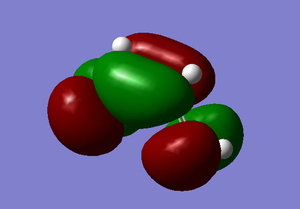
Ethene
Optimised Molecule	HOMO	LUMO

Energies / Hartree

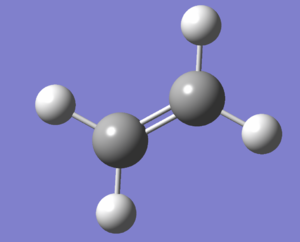
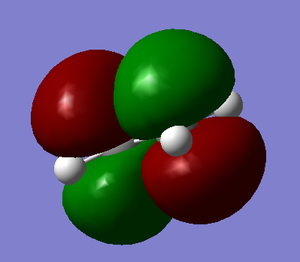
Cis-Butadiene		Ethene
AM1 Optimisation	B3LYP/6-31G* Optimisation	AM1 Optimisation	B3LYP/6-31G* Optimisation
0.04879719	-155.98595120	0.02619028	-78.58745783

Using the Guess Method and a HF/3-21G level of theory, the transition state was computed. As expected, a negative (imaginary) frequency was found at -818.36cm^-1 , which gives rise to bond formation, and the lowest vibration frequency was at 166.59cm^-1. The former gives a synchronous vibration whilst the latter gives an asynchronous one. The lowest vibration does not show a compression or elongation of the fragment distances, suggesting that it's not involved in the formation of the bonds.

(Why did you switch to HF for the TS? Tam10 (talk) 10:23, 3 February 2016 (UTC))

Negative Frequency	Lowest Frequency

The geometry of the transition state is as follows:

Structure	Bond lengths/Å		Angles/ ˚
	C1-C3	1.39944	C8-C14-C11 and C5-C11-C14	109.142
	C1-C5 and C3-C8	1.37001	C1-C3-C8 and C5-C1-C3	121.473
	C5-C11 and C8-C14	2.20957	C1-C5-C11 and C3-C8-C14	101.590
	C14-C11	1.37588

Usually, sp³ C-C bond lengths are typically 1.54 ‎Å, sp² C=C bond lengths are 1.34 ‎Å and the van der Waals radius of Carbon is 1.7 ‎Å. As can be seen in the table, the partially formed bonds are smaller than 2xVdW radius which indicated there is some interaction. The other C-C bonds in the transition states are all smaller than 1.54Å but bigger than 1.34Å, showing that there is delocalisation in the transition state.

The HOMO and LUMO of the transition state were also computed. It can be seen the the LUMO is symmetric and has been formed by the HOMO of ethylene and the LUMO of cis-butadiene. The HOMO is anti-symmetric and has been formed by the HOMO of cis-butadiene and LUMO of ethylene:

HOMO	LUMO

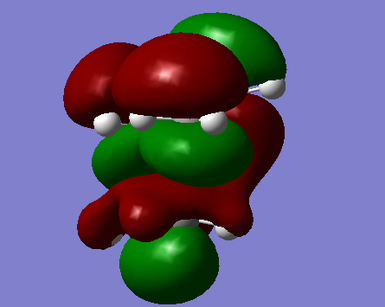
The IRC was calculated and the results are shown below, together with the animation of formation of the two sigma bonds:

Total Energy and RMS Gradient Norm along IRC	Animation of bond formation

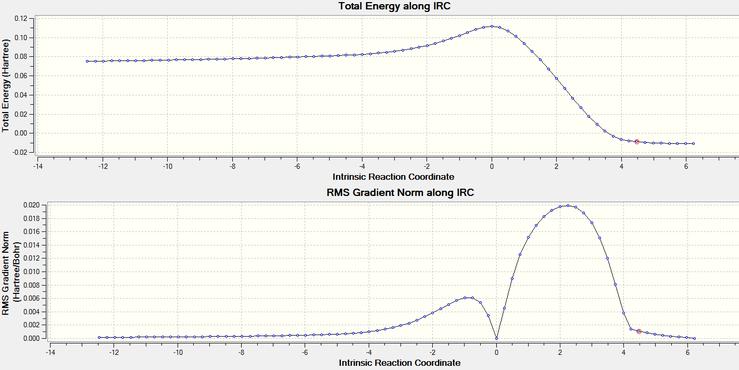
Regioselectivity

The Diels-Alder reaction can proceed via two different transition states, exo and endo. In the endo TS, the substituents of the dienophile are orientated towards the diene

$\pi$

system whilst in the exo TS, they are orientated away from it. Usually, the endo TS is preferred under kinetic conditions.

In this section, the reaction between cyclohexa-1,3-diene and maleic anhydride will be used to study this regioselectivity. The two possible paths, endo and exo, can be seen in the image below.

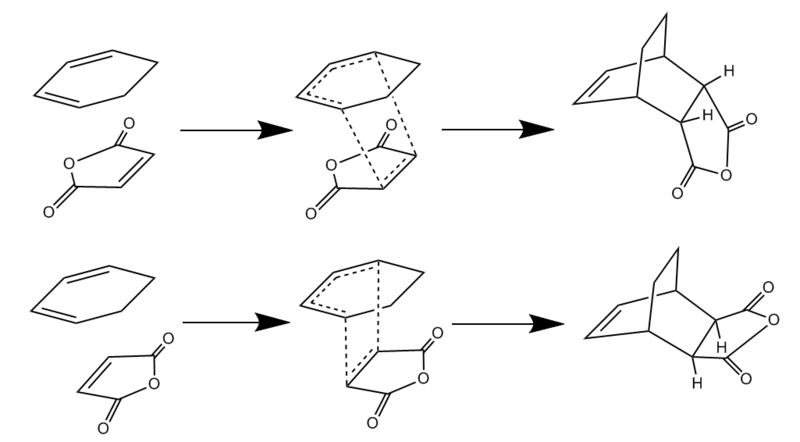
First, both maleic anhydride and cyclohexa-1,3-diene were modelled using GaussView and optimised to a minimum using the AM1 Semi-empirical method. Then, they were arranged in an endo or exo fashion.

Endo Transition State

The endo TS was modelled in GaussView using the two optimised starting materials. They were placed at about 2.2Å from each other in the following arrangement:

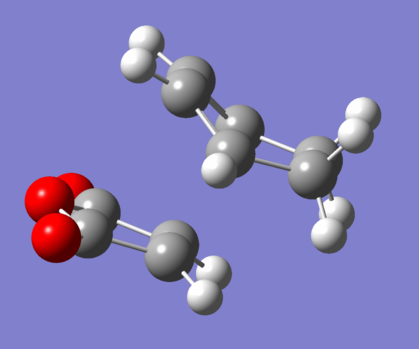
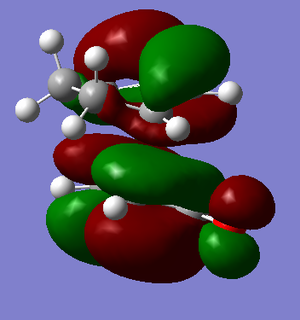
This structure was optimised to a TS (Berny) using the Semi-empirical AM1 method, which confirmed that it was indeed a transition state since one negative frequency was found at -806.39cm^-1. The bond length of the partially formed bonds was 2.26858Å. The HOMO and LUMO can be seen below, together with the vibration corresponding to the imaginary frequency:

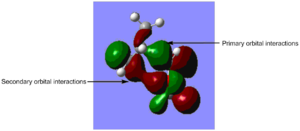
Imaginary Frequency	HOMO	LUMO

Exo Transition State

The maleic anhydride and the cyclohexa-1,3-diene were then arranged in an exo manner and the structure was optimised to a TS(Berny) using the Semi-empirical AM1 method. A negative frequency was found at -812.19cm^-1 (which can be seen down below). The bond length partially formed bonds was 2.17Å. The HOMO and the LUMO of the TS can be seen in the table below:

Imaginary Frequency	HOMO	LUMO

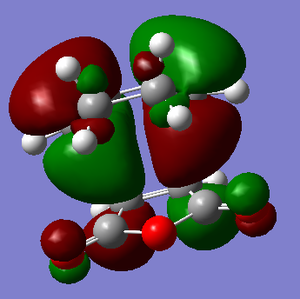
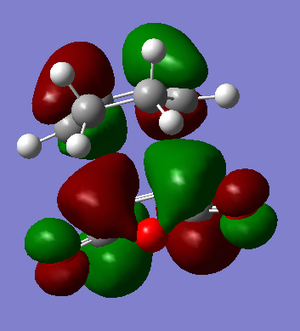
Energies/Hartree
	Electronic Energy	Sum of electronic and zero-point energies (0K)	Sum of electronic and thermal energies (298.15K)
Cyclohexa-1,3-diene	-0.0161948	0.131868	0.137448
Maleic Anhydride	-0.12182418	-0.063346	-0.058192
Exo TS	-0.05041985	0.134881	0.144881
Endo TS	-0.05150480	0.133494	0.143683

(Your calculations here are using the energies from cyclohexene, compared to cyclohexadiene. This is why your activation energies are too high Tam10 (talk) 10:23, 3 February 2016 (UTC))

To calculate the activation energies the energies of the two reactants were combined and the energy of the TS was subtracted and then the result multiplied by 627.509 (1 Hartree = 627.509 kcal/mol).

Activation Energies in K/kcal/mol
	At 0K	At 298.5K
Exo	41.64	41.18
Endo	40.77	40.42

It is clear that, at both temperatures, the endo pathway is lower in energy with respect to the exo pathway. Therefore, if the Diels-Alder reaction is under kinetic control, the endo product will be the major product. This could be due to secondary orbital overlap between the π systems of the -(C=O)-O-(C=O)-and the -CH-CH- fragments. Nevertheless, it can be seen than the π orbitals of these two fragments are out of phase in the HOMO and therefore the secondary orbital interaction is not likely to take place.

Conclusion

In the first part of this experiment the Cope Rearrangement was studied. Two levels of theory were used: 3-21G and 6-31G* which showed to give a similar structure but a significant difference in energy. Different methods were used to optimise the structures and obtain a feasible transition state and to confirm that we had indeed obtained a transition state structure, an IRC was calculated, which mapped the path to the lowest energy geometry. The frequencies were also computed, together with the energies (both at 0K and at 298.15K). The presence of a negative vibration confirmed the existence of a transition state structure and the energies allowed us to calculate the activation energy of the reaction, which is really important when determining which path is more likely under kinetic conditions.

In the second part, various Diels-Alder reactions were examined. This time, the semi-empirical AM1 level of theory was used in order to minimise the expense of the calculations. First, the starting materials were optimised to a minimum and then were used to 'guess' the transition state structures, which were optimised to a TS (Berny). The energies were also calculated and the activation energies showed that the endo product is favoured as long as the reaction is under kinetic conditions. It was seen that, due to the phase of the π orbitals in the HOMO, a second orbital interaction was unlikely. Therefore, a possible reason to justify the endo preference could be the increased steric hindrance between the ring structure and the oxygen atoms on maleic anhydride in the exo transition state structure.

(Could you demonstrate the steric hindrance? Tam10 (talk) 10:23, 3 February 2016 (UTC))

All these calculations involved several approximations, that resulted in less accurate results that need to be treated carefully. The electron-nuclei interaction were all ignored, using the Born-Oppenheimer Approximation which states that the nuclei can be assumed to be stationery due to its significant larger size with respect to the electron.