Rep:Mod:als15TS

Introduction

Potential Energy Surfaces

A potential energy surface, PES, is a plot of potential energy, V, as a function of nuclear separation, r. In the case of a non-linear molecule, there are 3N-6 degrees of freedom, where N is the number of atoms, and there are 3N-5 degrees of freedom in a linear molecule. Minima, where configurations of reactants and products lie, are defined mathematically as a stationary point, $\frac{\partial V}{\partial r_{i}} = 0$ , where all the second derivatives are positive, $\frac{\partial^{2} V}{\partial r_{i}^{2}} > 0$ . A transition state is a maximum in a minimum energy path between two minima. Mathematically, they are defined as stationary points where only one of the second derivatives is negative; the rest being positive.

Nf710 (talk) 10:11, 21 February 2018 (UTC) This info can be found by diagonalising the hessain

Vibrational Frequencies^[1]

The vibrational wavenumber, $\bar{ν}$ , is related to the force constant, k, in the equation:

\bar{ν} =

\frac{1}{2 π c}

\sqrt{\frac{k}{μ}}

,

where c is the speed of light in vacuum, μ is the reduced mass of the molecule and k is the force constant, which is equal to the second derivative in a PES. A structure at a minimum would therefore have all positive vibrational frequencies and a transition state structure would have one negative vibrational frequency. If there are more than one negative vibrational frequencies, the structure has a maximum potential energy in more than one dimension and this means there is a lower energy path connecting the two minima (via the transition state). When the transition state is found, a reaction profile - energy versus the degree of freedom where the TS is at a maximum - can be plotted.

PM6 and B3LYP [1]

In the Hartree-Fock model, an MO is expressed as a linear combination of AOs, $ψ =$ $\sum c_{i}$ $ϕ_{i}$ , where the coefficients are found by minimising the expectation value of energy of the MO, which is called variational theory. In practice, instead of using AOs from the solution of the Schroedinger equation for the hydrogen atom, slater-type orbitals of the form $e^{- a r}$ or gaussian-type orbitals of the form $e^{- a r^{2}}$ are used as they are easier to integrate, with gaussian-type orbitals being the easiest. In the semi-empirical method, PM6, some integrals are omitted and replaced with empirical parameters, making it computationally more efficient but less accurate. B3LYP is a hybrid between the Hartree-Fock model and density functional theory, where an N-electron wavefunction can be expressed as one-electron densities by integrating the N-electron wave function over all spin and spatial coordinates apart from the spatial coordinates of the electron in question as in:

ρ (r_{1}) = N \int | ψ (x_{1}, x_{2} . . . x_{N}) |^{2} d s_{1} d x_{2} . . . d x_{N}

,

where ρ is the one-electron density, N is the number of electrons in the system, x is the spin and spatial coordinates of an electron and s is the spin coordinate. B3LYP is a more expensive method than PM6, but yields greater accuracy.

Nf710 (talk) 10:18, 21 February 2018 (UTC) B3LYP is a hybrid method because it uses the DFT hamiltonian. but that doesnt account for 2 electron exchange correlation so it uses a F calculation (and some other stuff) to regain some of that.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Good job on this section, although you should have taken more care in ordering the MOs in your diagram with respect to the MO energies you have calculated. The bonding TS MOs are indeed higher in energy than what you report, while the antibonding TS MOs are lower in energy than what you report.)

MO Interaction

Figure 1 shows the interactions between the MOs of butadiene and ethene and the resulting MOs of the transition state. The MOs and relative energies of the reactants are a result of Huckel theory, where only π electrons are considered. The computed MOs of the transition state, MO16-MO19, show that interactions between HOMO(diene)-LUMO(dienophile) and HOMO(dienophile)-LUMO(diene) both occur. This happens due to the similar energies and same symmetry of the MOs in each pair. If one MO was anti-symmetric and the other symmetric, the orbital overlap would be zero as there would be equal amounts of bonding interaction as there would be anti-bonding interaction. Any overlap is cancelled and it leads to two non-bonding orbitals, i.e. no interaction between orbitals of opposite symmetry. A pair of MOs that are both symmetric or both asymmetric results in a non-zero overlap, and hence interaction occurs.

Table 1: HOMOs and LUMOs of butadiene and ethene

Butadiene

Ethene

HOMO

LUMO

Table 2: MOs in transition state of the reaction between butadiene and ethene

MO16 (HOMO-1)

MO17 (HOMO)

MO18 (LUMO)

MO19 (LUMO+1)

C-C Bond Lengths

Table 3 shows how the carbon-carbon bond lengths, referred to in Figure 2, change as the reaction progresses. The bond lengths in the reactants and product are as expected when compared to typical carbon-carbon bond lengths of particular hybridisations, as seen in Table 4. The bond lengths in the transition state are more similar to that in the reactant, which suggests an early transition state. Furthermore, in the transition state, C1-C6 and C4-C5 are shorter than double the van der Waals radius of carbon (3.40Å), which means the two bonds have partially formed in the transition state. They are also the same length, which suggests bond formation is synchronous, as can be seen in the negative frequency vibrational mode in Figure 3.

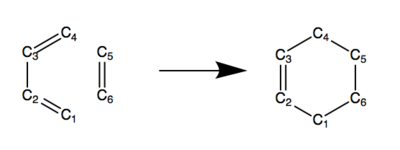
Table 3: Bond lengths as the reaction progresses

	Bond Length / Å
	Reactants	Transition State	Product
C1-C2	1.33349	1.37979	1.50087
C2-C3	1.47077	1.41109	1.33698
C3-C4	1.33343	1.37977	1.50079
C4-C5	-	2.11482	1.53717
C5-C6	1.32741	1.38177	1.53467
C6-C1	-	2.11466	1.53708

Table 4: Typical C-C bond lengths ^[2]

	Typical Length / Å
C(sp3)-C(sp3)	1.54
C(sp2)-C(sp3)	1.50
C(sp2)-C(sp2)	1.47
C(sp2)=C(sp2)	1.34
C van der Waals radius	1.70

Figure 3: Negative frequency of vibration at the transition state showing bond formation is synchronous.

Exercise 2: Cyclohexadiene and 1,3-Dioxole

MO Diagram

Table 5 and 6 show transition state MOs, optimised at the B3LYP level, for both the exo and endo approach respectively. For a given approach, the relative energies of the reactant MOs, as seen in Table 7, were found by running a single point energy calculation of the first frame of the IRC (optimised at a PM6 level). For both the exo and endo approach, the LUMO of the 1,3-dioxole is higher in energy than that of cyclohexadiene, and the same can be seen for the HOMOs. This is a sign of an inverse electron demand Diels-Alder reaction. The electron donating ether groups on the 1,3-dioxole increase the energy of the frontier MOs of 1,3-dioxole as it donates more electron density to the alkene via pi interactions between the O p-orbital and C p-orbitals in the alkene.

Nf710 (talk) 10:23, 21 February 2018 (UTC) well done for doing this part. This is the correct way to show the electron demand of the reaction. As the relative energies in the hamiltonian are the same because both reactants are on the same surface.

Table 5: HOMO, HOMO-1, LUMO and LUMO-1 of exo transition state, optimised to B3LYP level.

HOMO-1 (MO40)

HOMO (MO41)

LUMO (MO42)

LUMO+1 (MO43)

Table 6: HOMO, HOMO-1, LUMO and LUMO-1 of endo transition state, optimised to B3LYP level.

HOMO-1 (MO40)

HOMO (MO41)

LUMO (MO42)

LUMO+1 (MO43)

Table 7: Energies of MOs relative to others in the same approach (endo or exo).

	Energy of MO (exo)/ a.u.	Energy of MO (endo)/ a.u.
LUMO of 1,3-dioxole	0.02979	0.03219
LUMO of Cyclohexadiene	0.02111	0.02288
HOMO of 1,3-dioxole	-0.32207	-0.31696
HOMO of Cyclohexadiene	-0.32217	-0.32135

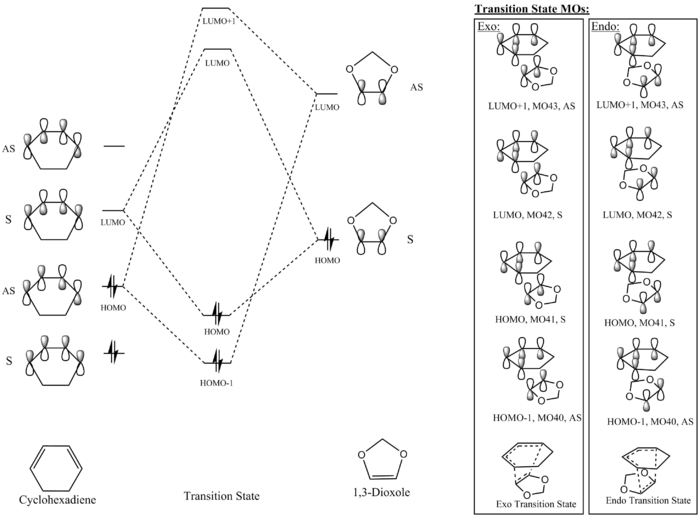
(Fv611 (talk) Your discussion and your computations have been done well but you have not taken into consideration your computed TS MO energies.)

Thermochemistry

Table 8 shows the reaction energies and reaction barriers for the endo and exo reaction between cyclohexadiene and 1,3-dioxole. The endo reaction is both kinetically and thermodynamically favourable, as it has a lower energy barrier and a more negative Gibbs free energy of reaction. The endo reaction is kinetically more favourable due to secondary orbital interactions. In the HOMO of the endo transition state the oxygen p-orbitals interact in-phase with carbon p-orbitals in the cyclohexadiene, as can be seen in Table 9 and Figure 5. These secondary orbital interactions lower the energy of the HOMO of the endo transition state. So, in comparison to the exo transtion state - where secondary orbital interactions are absent, the energy of the endo transition state and,therefore kinetic barrier, is lower.

Table 8: Gibbs free energy values at room temperature of structures optimised at B3LYP level.

	Gibbs Free Energy / Hartrees	Gibbs Free Energy / kJ mol^-1
Cyclohexadiene	-233.324375	-612593.19323
1,3-Dioxole	-267.068637	-701188.75986
Exo TS	-500.329163	-1313614.3175
Endo TS	-500.332150	-1313622.1599
Exo Product	-500.417322	-1313845.779
Endo Product	-500.418692	-1313849.3759
ΔG(exo)		-63.8259100
ΔG‡(exo)		167.635590
ΔG(endo)		-67.4228100
ΔG‡(endo)		159.793190

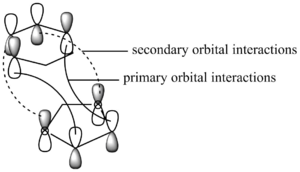
Table 9: HOMOs of the exo and endo transition states. There are secondary orbital interactions in the endo TS HOMO.

HOMO of Exo TS

HOMO of Endo TS

Nf710 (talk) 10:30, 21 February 2018 (UTC) This was a very good section and your diagrams very nicely complemented your discussion on the thermodynamics of the reaction.

Exercise 3: Xylylene and SO₂

The possible reactions between xylylene and SO₂ are shown in Figure 6 and the reaction barriers and reaction energies are shown in Table 10. The exo and endo reactions have the same reaction barrier and reaction energy, which makes sense as the bonding and sterics in the transition states and the products are similar. The chelotropic reaction is thermodynamically more favourable, but kinetically less favourable, than the exo and endo reactions. The more stable product from the chelotropic reaction is due to the S=O bond being stronger than a C-S bond and S-O bond combined. In all three of these reactions, the reaction energies are negative, which is due to the aromatisation of the six-membered ring in xylylene, as shown in the IRCs in Figure 7-9 by the bond order of 1.5 in the product. The two reactions of SO₂ with the alternative diene (Alternative 1 and 2 in Figure 6) are the most kinetically unfavourable and the most thermodynamically unfavourable due to the steric hindrance in the transition states and the fact that the six-membered ring is not aromatised.

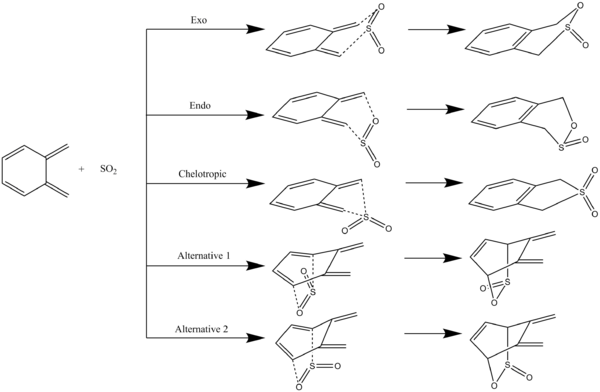
Figure 7: IRC of the exo reaction between xylylene and SO₂

Figure 8: IRC of the endo reaction between xylylene and SO₂

Figure 9: IRC of the chelotropic reaction between xylylene and SO₂

Table 10: Energies of the reactants, transition states and products of the exo, endo, chelotropic, alternative 1 and alternative 2 reaction between xylylene and SO₂.

	Exo	Endo	Chelotropic	Alternative 1	Alternative 2
Xylylene	467.266
SO2	-311.421
TS	241.746	241.746	260.087	267.985	275.822
Product	56.3275	56.3327	0.013128	172.256	176.709
ΔG	-99.5175	-99.5123	-155.832	16.4110	20.8640
ΔG‡	85.9010	85.9010	104.242	112.140	119.977

(Your endo and exo TSs and products are actually both the exo Tam10 (talk) 16:16, 19 February 2018 (UTC))

LOG Files

Exercise 1:

Ethene PM6	Media: als15_ALKENE_MIN_PM6.LOG
Butadiene PM6	Media: als15_BUTADIENE_MIN_PM6.LOG
Guess TS PM6	Media:als15_FROZENGUESSTS_MIN_PM6.LOG
Transition State PM6	Media:als15_GUESSTS_TSBERNY_PM6.LOG
IRC PM6	Media:als15_IRC_PM6.LOG
Cyclohexene PM6	Media:als15_PRODUCT_MIN_PM6.LOG

Exercise 2:

1,3-Dioxole PM6	Media:als15_13DIOXOLE_MIN_PM6.LOG
1,3-Dioxole B3LYP	Media:als15_13DIOXOLE_MIN_B3LYP.LOG
Cyclohexadiene PM6	Media:als15_CYCLOHEXADIENE_MIN_PM6.LOG
Cyclohexadiene B3LYP	Media:als15_CYCLOHEXADIENE_MIN_B3LYP.LOG
Endo Guess TS PM6	Media:als15_ENDO_FROZENTS_MIN_PM6.LOG
Endo Transition State PM6	Media:als15_ENDO_GUESSTS_TSBERNY_PM6.LOG
Endo Transition State B3LYP	Media:als15_ENDO_GUESSTS_TSBERNY_B3LYP.LOG
Endo IRC PM6	Media:als15_ENDOTS_PM6_IRC.LOG
Endo Product PM6	Media:als15_ENDOPRODUCT_MIN_PM6.LOG
Endo Product B3LYP	Media:als15_ENDOPRODUCT_MIN_B3LYP.LOG
Exo Guess TS PM6	Media:als15_EXO_FROZENTS_MIN_PM6.LOG
Exo Transition State PM6	Media:als15_EXO_GUESSTS_TSBERNY_PM6.LOG
Exo Transition State B3LYP	Media:als15_EXO_GUESSTS_TSBERNY_B3LYP.LOG
Exo IRC PM6	Media:als15_EXOTS_PM6_IRC.LOG
Exo Product PM6	Media:als15_EXOPRODUCT_MIN_PM6.LOG
Exo Product B3LYP	Media:als15_EXOPRODUCT_MIN_B3LYP.LOG

Exercise 3:

Xylylene PM6	Media:als15_XYLYLENE_MIN_PM6.LOG
SO₂ PM6	Media:als15_SO2_MIN_PM6.LOG
Exo Guess TS PM6	Media:als15_EXO_FROZENTS_MIN_PM6.LOG
Exo Transition State PM6	Media:als15_EXO_GUESSTS_TSBERNY_PM6.LOG
Exo Product PM6	Media:als15_EXO_PRODUCT_MIN_PM6.LOG
Exo IRC PM6	Media:als15_EXO_TS_PM6_IRC.LOG
Endo Guess TS PM6	Media:als15_DAENDO_FROZENTS_MIN_PM6.LOG
Endo Transition State PM6	Media: als15_DAENDO_GUESSTS_TSBERNY_PM6.LOG
Endo Product PM6	Media:als15_DAENDO_PRODUCT_MIN_PM6.LOG
Endo IRC PM6	Media:als15_DAENDO_TS_PM6_IRC.LOG
Chelotropic Guess TS PM6	Media:als15_CHELO_FROZENTS_MIN_PM6.LOG
Chelotropic Transition State PM6	Media:als15_CHELO_GUESSTS_TSBERNY_PM6.LOG
Chelotropic Product PM6	Media:als15_CHELO_PRODUCT_MIN_PM6.LOG
Chelotropic IRC PM6	Media: als15_CHELO_TS_IRC_PM6.LOG
Alternative 1 Guess TS PM6	Media:als15_ALTLEFT_FROZENTS_MIN_PM6.LOG
Alternative 1 Transition State PM6	Media:als15_ALTLEFT_GUESSTS_TSBERNY_PM6.LOG
Alternative 1 Product PM6	Media: als15_ALTLEFT_PRODUCT_MIN_PM6.LOG
Alternative 1 IRC PM6	Media:als15_ALTLEFT_TS_PM6_IRC.LOG
Alternative 2 Guess TS PM6	Media:als15_ALTRIGHT_FROZENTS_MIN_PM6.LOG
Alternative 2 Transition State PM6	Media:als15_ALTRIGHT_GUESSTS_TSBERNY_PM6.LOG
Alternative 2 Product PM6	Media: als15_ALTRIGHT_PRODUCT_MIN_PM6.LOG
Alternative 2 IRC PM6	Media:als15_ALTRIGHT_TS_PM6_IRC.LOG

References

↑ McDouall, J. (2013). Computational Quantum Chemistry: Molecular Structure and Properties in Silico. p. 1-16. Royal Society of Chemistry.
↑ Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. p.159. Springer. ISBN 978-3-86025-249-9.

[1] McDouall, J. (2013). Computational Quantum Chemistry: Molecular Structure and Properties in Silico. p. 1-16. Royal Society of Chemistry.

[2] Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. p.159. Springer. ISBN 978-3-86025-249-9.

[1]

[2]