Jump to content

Rep:Mod:al7215

From ChemWiki

NH3 Molecule

NH3 Molecule Optimisation
Information
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ a.u -56.55776873
RMS Gradient 0.00000485
Point Group C3V
Click here for the Log File.

Optimised N-H bond distance for NH3 molecule: 1.01798 Å

Optimised H-N-H bond angle for NH3 molecule: 105.741o 

         Item             Value        Threshold    Converged?

 Maximum Force            0.000004     0.000450     YES

 RMS     Force            0.000004     0.000300     YES

 Maximum Displacement     0.000072     0.001800     YES

 RMS     Displacement     0.000035     0.001200     YES
Vibrational and Charge Analysis of NH3 Molecule

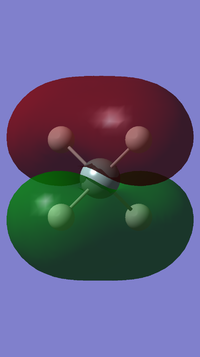
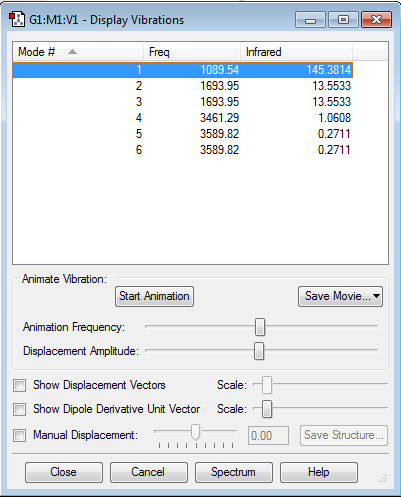
Number of modes expected from 3N-6 ruleː 6

Degenerate modesː Modes 2 and 3 are degenerate; Modes 5 and 6 are degenerate as well.

Bending vibration modesː Modes 1, 2 and 3

Bond stretching vibration modesː Modes 4, 5 and 6

Highly symmetric modeː Mode 4

"Umbrella" modeː Mode 1

Expected number of experimental spectrum bands of gaseous ammoniaː 2 bands, one due to vibration mode 1 and another due to vibration modes 2 and 3. The infrared intensity due to vibration modes 4, 5 and 6 are 1.0608, 0.2711 and 0.2711 respectively. Bands due to these vibration modes are most likely absent from the experimental spectrum as they are extremely low in intensity and can hardly be detected by the instrument.

Expectation of Charge for N and H atoms:The specific Natural Bond Orbital (NBO) charges were analysed for the optimised NH3 molecule. Nitrogen has a negative charge of -1.125 while hydrogen has a positive charge of 0.375. This charge distribution is expected as nitrogen is more electronegative than hydrogen, thus leading to the withdrawal of electrons from the four coordinating hydrogen atoms by nitrogen. Additionally, all four hydrogen atoms have the same charge as all N-H bond lengths are equal.

N2 and H2 Molecules

N2 Molecule Optimisation
Information
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ a.u -109.52412868
RMS Gradient 0.00000060
Point Group D∞h
Click here for the Log File. 
         Item             Value        Threshold    Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
Vibrational and Charge Analysis of N2 Molecule

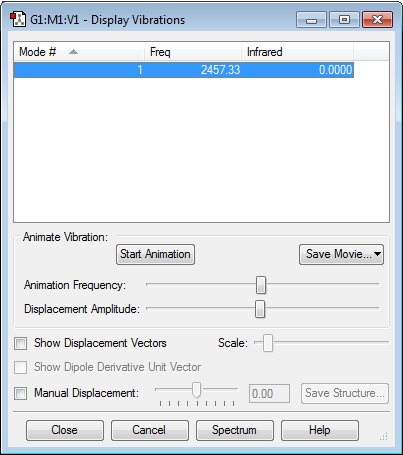
There are no negative frequencies. Infrared intensity is zero as there is no change in dipole moment due to symmetric stretching of N2 molecule. Additionally, since there is no electronegativity difference between the two atoms as N2 is a homonuclear diatomic molecule, both atoms will have zero charge.


H2 Molecule Optimisation
Information
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ a.u -1.17853936
RMS Gradient 0.00000017
Point Group D∞h
Click here for the Log File. 
         Item             Value        Threshold    Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
Vibrational and Charge Analysis of H2 Molecule

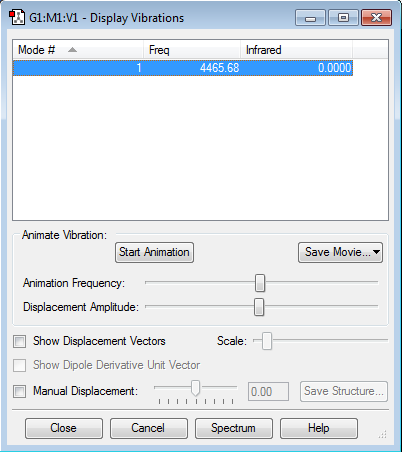
Similarly, there are no negative frequencies. Infrared intensity is zero as there is no change in dipole moment due to symmetric stretching of H2 molecule. Additionally, since there is no electronegativity difference between the two atoms as H2 is a homonuclear diatomic molecule, both atoms will have zero charge.

Reaction Energies

Reaction: N2 + 3H2 -> 2NH3

E(NH3) = -56.55776873 a.u.

2*E(NH3) = -113.11553746 a.u.

E(N2) = -109.52412868 a.u.

E(H2) = -1.17853936 a.u.

3*E(H2) = -3.53561808 a.u.

ΔE=2*E(NH3)-[E(N2)+3*E(H2)] = -0.0557907 a.u. = -146.4784829 kJ/mol = -146.48 kJ/mol (2 decimal places)

The energy for converting hydrogen and nitrogen gas into ammonia gas is -146.48 kJ/mol (2 decimal places). The literature value for this Haber process is -109 kJ/mol at 500oC. [1] A possible explanation for the large deviation between the computed and literature value is that the NH3 molecule is set to be under an isolated gas phase for computational analysis, whereas experimentally, NH3 molecule is surrounded by other NH3 molecules. Additionally, temperature also has an effect on how exothermic this reaction would be, which cannot be properly accounted for with computational analysis. This ultimately shows us that simple Density Function Theory (DFT) method is insufficient to help us calculate thermodynamic data.

Since this is an exothermic reaction, the gaseous reactants are at a higher energy level than the ammonia product. Therefore, the ammonia product is more stable than the gaseous reactants.

SiH4 (Silane) Molecule

SiH4 Molecule Optimisation
Information
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ a.u -291.88802760
RMS Gradient 0.00000002
Point Group Td
Click here for the Log File. 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

Optimised Si-H bond distance for SiH4 molecule: 1.48485 Å

Optimised H-Si-H bond angle for SiH4 molecule: 109.471o

Frequency and Vibrational modes of SiH4

No. Image Frequency (cm-1) Infrared Brief description
1
919.21 136.1485 Asymmetric Scissoring. Threefold degeneracy due to symmetry of system and three different scissoring motions. As intensity is non-zero, these are infrared active vibration modes due to a change in dipole moment.
2
919.21 136.1485
3
919.21 136.1485
4
978.78 0.0000 Symmetric Scissoring. Twofold degeneracy due to symmetry of system and two different scissoring motions. As intensity is zero, these two vibration modes are infrared inactive as there is no change in dipole moment.
5
978.78 0.0000
6
2244.40 0.0000 Symmetric Stretching. As intensity is zero, this vibration mode is infrared inactive as there is no change in dipole moment.
7
2254.90 143.3961 Asymmetric Stretching. Threefold degeneracy due to symmetry of system and three different ways of stretching. As intensity is non-zero, these are infrared active vibration modes due to a change in dipole moment.
8
2254.90 143.3961
9
2254.90 143.3961

Charge Analysis for SiH4

Charge distribution
The specific Natural Bond Orbital (NBO) charges were analysed for the optimised SiH4 molecule. Silicon has a positive charge of 0.629 while Hydrogen has a negative charge of -0.157. This charge distribution is expected as hydrogen is more electronegative than silicon, thus leading to the withdrawal of electrons from the silicon center by the four coordinating hydrogen atoms. Additionally, all four hydrogen atoms have the same charge as all Si-H bond lengths are equal.

Molecular Orbital (MO) Analysis of SiH4

Molecular Orbitals Image Energy (a.u.) Description
2 -5.28056 Molecular orbital (MO) 2 is a very low energy, occupied MO of silane. This MO is completely around the silicon atom and is non-bonding due to its sole atomic orbital contribution by silicon's 2s atomic orbital.
6 -0.54726 Molecular orbital (MO) 6 is a low energy, occupied MO of silane. The atomic orbital interactions are 3s atomic orbital of silicon atom being in-phase with all 4 1s atomic orbitals of hydrogen atom. The interactions are bonding, with no nodes present.
7 -0.35184 Molecular orbital (MO) 7 is the Highest Occupied Molecular Orbital (HUMO) of silane. It is triply degenerate with MO 8 and MO 9 due to symmetry of the molecule and the possibility of orientation along different directions. The atomic orbital interactions for this orbital are 3p atomic orbital of silicon atom being in-phase with all 4 1s atomic orbitals of hydrogen atom. Additionally, the 2 hydrogen atom's 1s orbital are anti-phase with the other 2 hydrogen atom's 1s atomic orbital. The interactions are bonding, with a planar node runnning through the center of the molecule.
10 0.05053 Molecular orbital (MO) 10 is the Lowest Unoccupied Molecular Orbital (LUMO) of silane. This MO is triply degenerate with MO 11 and MO 12 due to symmetry of the molecule and the possibility of orientation along different directions. The atomic orbital interactions for this orbital are 3p atomic orbitals of silicon atom being anti-phase with all 4 1s atomic orbitals of hydrogen atom. Moreover, similar to MO 3, the 2 hydrogen atom's 1s orbital are anti-phase with the other 2 hydrogen atom's 1s atomic orbital. The interactions are anti-bonding, with a nodal region separating the two phases.
13 0.12286 Molecular orbital (MO) 13 is a higher in energy, unoccupied MO of silane. The atomic orbital interactions for this orbital are 3s atomic orbital of silicon being anti-phase with all 4 1s atomic orbitals of hydrogen. The interactions are anti-bonding, with a spherical nodal region separating the 4 hydrogen atoms from the center silicon atom. Due to its large size and presence of a nodal region, it is high in energy.
Figure 1: Molecular Orbital Diagram of SiH4 (from Gaussview)
Figure 2: Molecular Orbital Diagram of SiH4 [2]

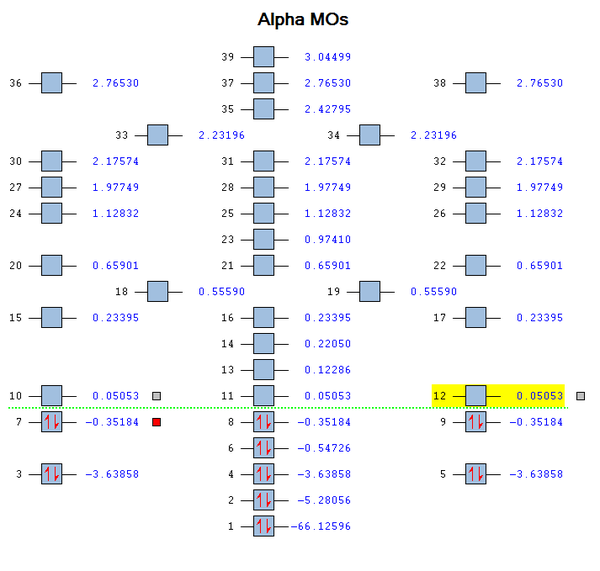
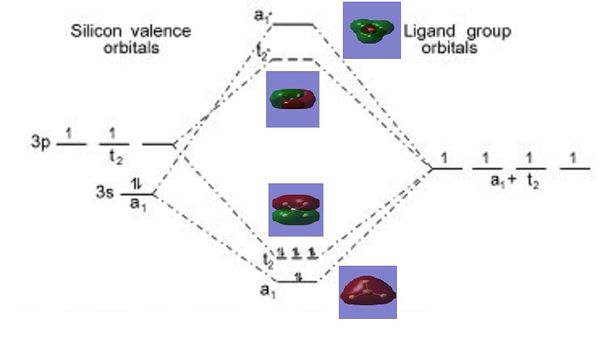
Figure 2 shows the ordering of the various energy levels with their corresponding molecular orbitals generated in gaussview. As a further study, the linear combination of atomic orbitals (LCAO) can also be compared with the computed molecular orbitals to show that the LCAO theory is a fairly good method to predict molecular orbitals for an unknown simple molecule without having to do complicated calculations.

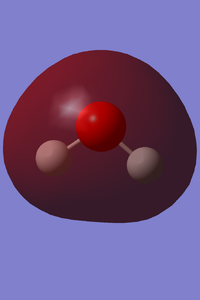
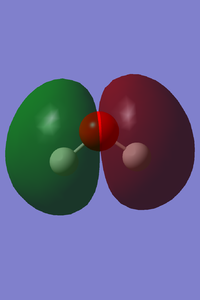
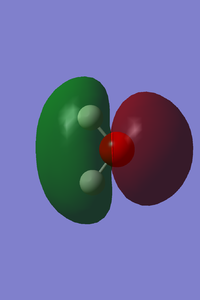
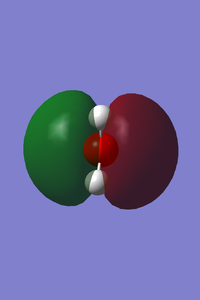
H2O Molecule

H2O Molecule Optimisation
Information
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ a.u -76.41973740
RMS Gradient 0.00006276
Point Group C2V
Click here for the Log File. 
         Item             Value        Threshold  Converged?
 Maximum Force            0.000099     0.000450     YES
 RMS     Force            0.000081     0.000300     YES
 Maximum Displacement     0.000114     0.001800     YES
 RMS     Displacement     0.000119     0.001200     YES

Optimised O-H bond distance for H2O molecule: 0.96522 Å

Optimised H-O-H bond angle for H2O molecule: 103.745o

Vibrational and Charge Analysis of H2O Molecule

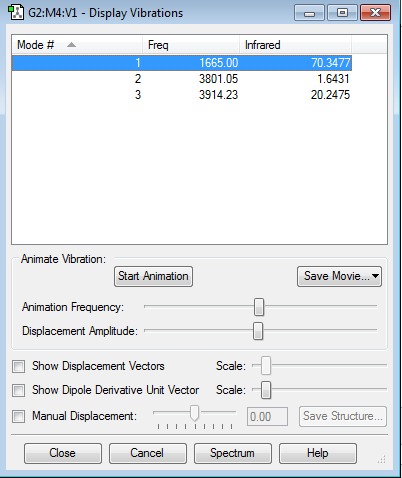
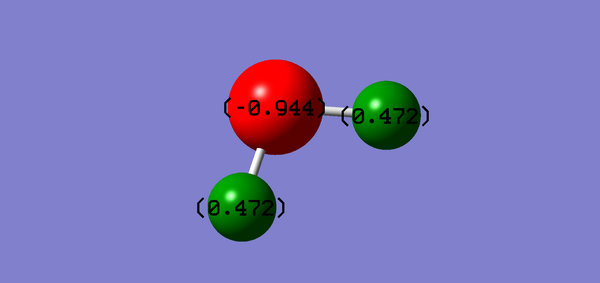
Molecular Orbital (MO) Analysis of H2O

Molecular Orbitals Image Energy (a.u.) Description
1 -19.13799 Molecular orbital (MO) 1 is a very low energy, occupied MO of H2O. This MO is completely around the H2O atom and is non-bonding due to its sole atomic orbital contribution by oxygen's 1s atomic orbital.
2 -0.99736 Molecular orbital (MO) 2 is a low energy, occupied MO of H2O. The atomic orbital interactions are 2s atomic orbital of oxygen atom being in-phase with the 2 1s atomic orbitals of hydrogen atom. The interactions are bonding, with no nodes present.
3 -0.51503 Molecular orbital (MO) 3 is also a low energy, occupied MO of H2O. The atomic orbital interactions are 2p atomic orbital of oxygen atom being in-phase with the 2 1s atomic orbitals of hydrogen atom. However, both of the hydrogen atom's 1s orbital are anti-phase with one another. The interactions are bonding, with a planar node runnning through the center of the molecule.
4 -0.37102 Molecular orbital (MO) 4 is another low energy, occupied MO of H2O. The atomic orbital interactions are 2p atomic orbital of oxygen atom being in-phase with the 2 1s atomic orbitals of hydrogen atom. Both of the hydrogen atom's 1s orbital are in-phase with one another. The interactions are bonding, with a planar node runnning through the center of the molecule.
5 -0.37102 Molecular orbital (MO) 5 is the Highest Occupied Molecular Orbital (HOMO) of H2O. This MO is non-bonding due to its sole atomic orbital contribution by oxygen's 2p atomic orbital.

References

  1. ↑ G. Marnellos and M. Stoukides, Science (80-. )., 1998, 282, 98–100.
  2. ↑ I. S. Baibich, Ione M; Butler, Quim. Nova, 2012, 35, 1474–1476.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:al7215&oldid=818542"