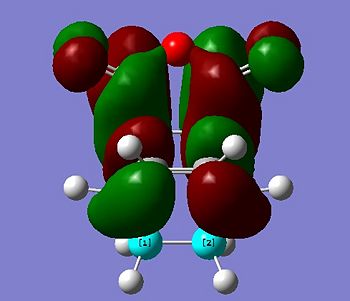
Rep:Mod:ajm3081989
James Marks ( ajm308 / 00548888 ) - {10/02/2011 - 18/02/2011}
Introduction
Computations will be carried out in order to characterise the transition states involved in both the Cope rearrangement and the Diels-Alder cycloaddition reactions.
Force field and molecular mechanics methods used in previous experiments are unsuitable for characterising transition states as they are unable to adequately describe the processes of bond making and bond breaking, as well as change in bonding type and electron distribution.
Molecular orbital based methods must be used instead, which involve solving the Schrodinger equation numerically.
Reaction pathways and barrier heights can also be calculated, along with the structures of transitions states.
Cope Rearrangement
The Cope rearrangement is an example of a [3,3]-sigmatropic shift rearrangement.
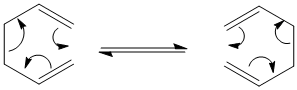
The Cope rearrangement of 1,5-hexadiene will be used as an example, to aid understanding of methods used in investigating chemical reactivity computationally.
The objective is to locate the low energy minima, as well as transition structures on the potential energy surface, in order to determine the preferred reaction mechanism.
It has previously been deduced, both experimentally and computationally, that the reaction proceeds in a concerted fashion via either one of two transition states - the 'chair' or the 'boat':

Optimising Reactants and Products
There a number of possible conformations of 1,5-hexadiene, with each having a distinct total energy.
Initially, 1,5-hexadiene was modeled in GaussView 03 with an 'anti' conformation. This structure was then optimised using the HF/3-21G method and basis set. The optimisation calculation was submitted to Gaussian. Having opened the output files in GaussView 03, the optimised structures were 'symmetrised' in order to determine point group.
The same method was followed on an initially 'gauche' conformation of 1,5-hexadiene. It was anticipated that the 'gauche' conformer would have a higher relative total energy than the 'anti' conformer, on account of the reduced steric repulsion in the arrangement. Initially this assumption was thought to be correct, as the optimised 'gauche' conformer did indeed have a higher relative total energy than the 'anti' conformer. On further investigation, the low energy conformer of 1,5-hexadiene was found to be a 'gauche' example. The lower relative total energy of this conformation can be accounted for by considering the possibility that favourable Van der Waal's interactions between hydrogen atoms are able to override the intrinsic steric strain within the conformation.
As the "anti 2" conformer was not located during initial optimisation, the conformer was modeled in GaussView 03, and optimised to yield the Ci symmetric 'anti' conformer. It was first optimised using the same HF/3-21G protocol, followed by further optimisation with the B3LYP/6-31G protocol. This second protocol is a more computationally intensive optimisation with a larger basis set, and thus could be expected to produce more accurate results.
A summary of the results and characteristics of all aforementioned calculations and conformers is included in the table below:
| Conformation | Theory level | Computed energy (a.u) | Appendix Value (a.u) | Symmetry Point Group | Structure | Conformer | |||
|---|---|---|---|---|---|---|---|---|---|
| Anti | HF/3-21G | -231.69 | -231.69 | C2 |
|
Anti 1 | |||
| Gauche | HF/3-21G | -231.69 | -231.69 | C2 |
|
Gauche 2 | |||
| Lowest Energy Conformer | HF/3-21G | -231.69 | -231.69 | C1 |
|
Gauche 3 | |||
| Ci Anti 2 conformation | HF/3-21G | -231.69 | -231.69 | Ci | Anti 2 | ||||
| Ci Anti 2 conformation | B3LYP/6-31G | -234.61 | -234.61 | Ci |
|
Anti 2 |
The two levels of theory, the more advanced B3LYP/6-31G and the more simple HF/3-21G, both returned optimised geometries that are superficially very similar. The difference in relative total energies of the two optimised "Anti 2" conformers was found to be 2.919 a.u.
Closer analysis of the optimised geometries was able to highlight slight differences between the two.
Dihedral angles were compared, as well as bond lengths.
| Atoms & Measurement | HF/3-21G | B3LYP/6-31G | Difference |
|---|---|---|---|
| 1,2,3,4 Dihedral angle | 114.626° | 118.53° | 3.904° |
| 2,3,4,5 Dihedral angle | 180.0° | 180.0° | 0° |
| 3,4,5,6 Dihedral angle | 114.626° | 118.53° | 3.904° |
| 1,2 Bond length | 1.316 A | 1.334 A | 0.018 A |
| 2,3 Bond length | 1.509 A | 1.504 A | 0.005 A |
| 3,4 Bond length | 1.552 A | 1.548 A | 0.004 A |
The more advanced protocol gives dihedral angles and bond lengths which differ from the less advanced protocol, but only to a slight extent, with bond lengths proving more reliable at the HF/3-21G level than the dihedral angles.
Frequency Calculations
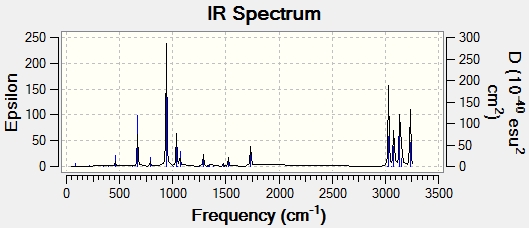
The B3LYP/6-31G optimised was then submitted to frequency calculations.
Frequency calculations, as shown in previous modules, are able to confirm that a minimum has been reached, by showing that all vibrational frequencies are positive and real.
Following frequency calculations at the same level of theory, the vibrational frequencies were all confirmed to be positive and real, with the computed IR Spectra shown below:
The output file was then used to find Thermochemical data. Four pieces of important data were noted.
A = The potential energy at 0 K, including zero-point vibrational energy. (E = Eelec + ZPE)
B = The energy at 298.15 K, 1 atm, including contributions from Translation, Rotational and Vibrational energy modes. (E = E + Evib + Erot + Etrans)
C = A correction for RT. (H = E + RT)
D = Includes the entropic contribution to free energy. (G = H - TS)
A. Sum of Electronic and Zero Point Energies: -234.47 a.u
B. Sum of Electronic and Thermal Energies: -234.46 a.u
C. Sum of Electronic and Thermal Enthalpies: -234.46 a.u
D. Sum of Electronic and Thermal Free Energies: -234.50 a.u
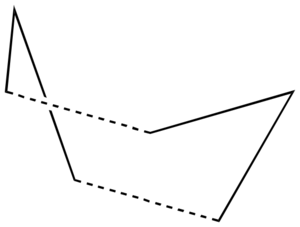
Chair and Boat Transition Structures
Chair
Initially an allyl (CH2CHCH2) fragment was modeled in GaussView 03, and optimised using the HF/3-21G protocol. The optimised fragment was then reproduced twice and the fragments were orientated such that they imitated the chair transition state.
This transition state was then manually optimised using two alternative methods. The optimisations become difficult as in order to compute, it is necessary for the method to have "knowledge" of where the negative direction of curvature (the reaction coordinate) is. Providing a reasonable guess has been made, the easiest way to obtain the required information is to compute the force constant matrix in the initial step of an optimisation, which can be updated as the optimisation proceeds. In some cases it is possible to generate a more accurate transition structure by freezing the reaction coordinate. Once the molecule is fully relaxed, reaction coordinate constraints can be removed, followed by optimisation of the transition state.
Optimisation to a TS (Berny)
The approximated transition state structure was optimised using the HF/3-21G protocol. The Job Type was chosen as 'Opt+Freq' and the method was further modified by changing 'Optimization to a Minimum' to 'Optimization to a TS (Berny)'. Force constants were set to calculate only once.
The calculation gave an imaginary frequency of -818 cm-1 as shown below:
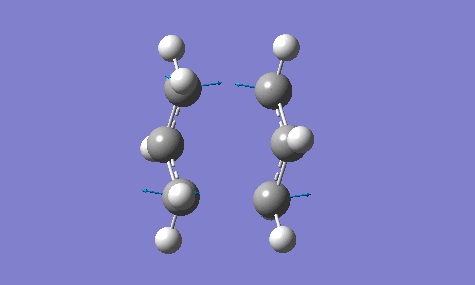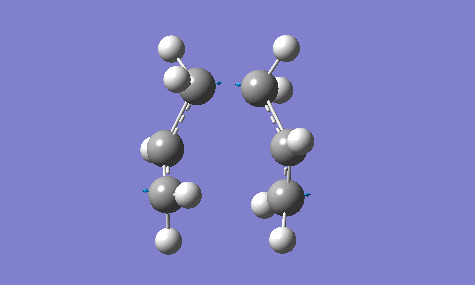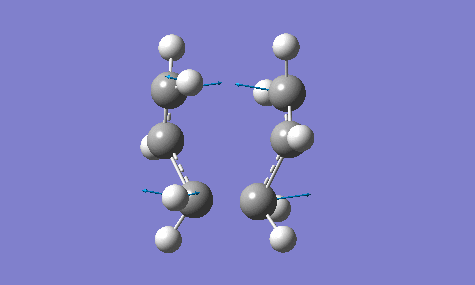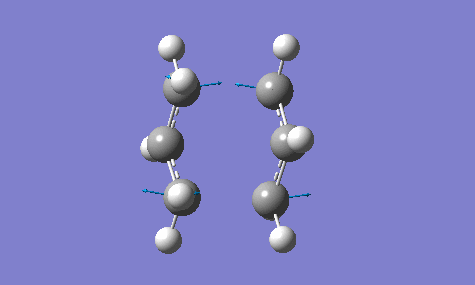
The optimised distance between terminals of the allyl fragments was found to be 2.02 A.
The Energy of the transition state was found to be -231.62 a.u.
Frozen Coordinate Method
The optimisation was then carried out using the frozen coordinate method. The approximated transition state structure was again used. The method outlined @ [1] was followed.
On completion of the submitted job, the output showed that the optimised structure was very similar to that found using the 'Optimisation to TS (Berny)' method, however it is noted that bond breaking/forming distances are fixed at 2.2 A. The constraints imposed before submitting the job were removed, and the transition state was optimised again.
The calculation gave an imaginary frequency of -818 cm-1 as shown below:
The optimised distance between terminals of the allyl fragments was found to be 2.02 A.
The Energy of the transition state was found to be -231.62 a.u.
Comparison
The two methods concur.
Although the two methods were both successful in this case, there are advantages and disadvantages to both.
The 'Optimisation to TS (Berny)' method requires an accurate approximate transition state in order to yield accurate results. For the simple case above this was relatively easy, however, in more complex systems it may not be as simple.
Although the frozen coordinate method does not require as accurate an initial transition state as the 'Optimisation to TS (Berny)' method, it is more computationally expensive.
Boat
Another method was then used to optimise the boat transition state. The method utilised was the QST2 method. Reactants and products are specified for the reaction and a computational interpolation will attempt to locate the transition state.
Again, the method located @ [2] was adhered to in order to prepare a Gaussian Input File.
The first QST2 calculation was then initiated. The Job Type was altered to 'Opt+Freq' and 'Optimise to a TS (QST2)'. This job was then submitted and failed. This failure highlights an inherent deficiency in the capability of computational chemistry. If the input file does not contain all the information required by the computational method, it will not succeed.
In order for the method to succeed the reactant and product geometries needed to be altered so that they more closely resemble the boat transition structure. The geometries were altered, with the central C-C-C-C dihedral angle being set to 0 o and the inside C-C-C angles set to 100 o.
The job was then resubmitted.
Only one imaginary vibrational frequency was returned, -840 cm-1 and the motion is shown below:
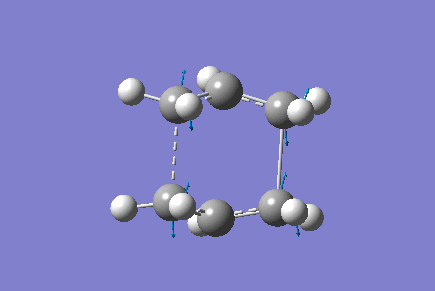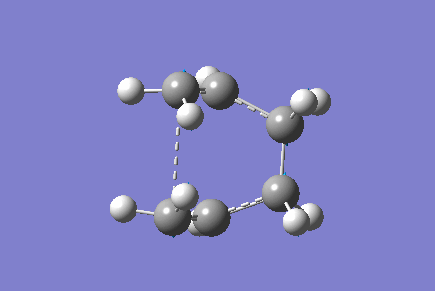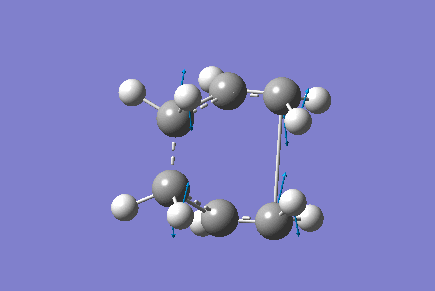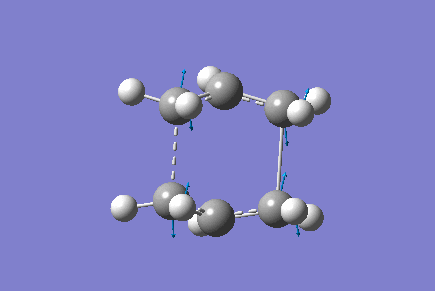
The optimised distance between terminals of the allyl fragments was found to be 2.14 A.
The Energy of the transition state was found to be -231.60 a.u.
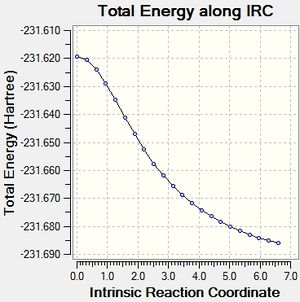
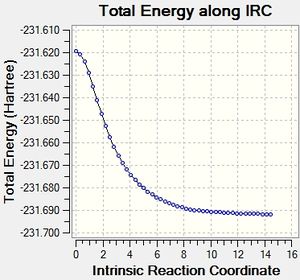
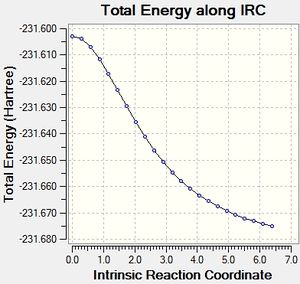
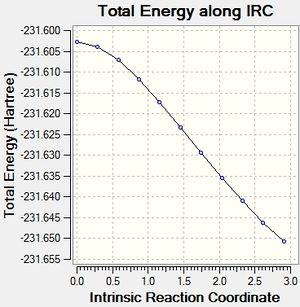
Intrinsic Reaction Coordinate Method
This method allows the following of the minimum energy path from the transition structure to its local minimum on the potential energy surface. A series of points is produced by taking small geometry steps in the direction of the steepest energy gradient. Initially it was chosen to run the method across 50 points on the potential energy surface, for both the chair and the boat transition states. The computation was run only in the forward direction due to the symmetry of the potential energy surface in this example. However, standard protocol is to run the method in both the forward and backward directions.
Chair
On opening the output file it was observed that no minimum had been reached in the computation.
Three options are then available:
1. Take the last point on the initial IRC and run a normal minimisation.
2. Restart the IRC and run with a larger number of points.
3. Specify that force constants should be computed at each step.
Approach 1 would be the least computationally costly, but the wrong minima may be found. Approach 2 is more reliable, but again, problems related to finding the wrong structure can present if too many points are required. Approach 3 is the most computationally expensive, but also the most reliable. It was decided to complete the IRC method using approached 1 and 3. The results for the chair transition state are shown in the table below:
Approach 1 yielded the lowest energy minima, with the method being far more efficient than Approach 3. The chair transition structure was shown to minimise to the 'Gauche 2' conformation.
Boat
The same methodology was applied to the Boat transition structure. Results are shown in the table below:
Further Analysis
Both the Chair and Boat transition structures were reoptimised using the more advanced B3LYP/6-31G protocol, with frequency analysis also being performed. The two methods utilised are compared in the tables below:
| Chair | ||
|---|---|---|
| Property | HF/3-21G | B3LYP/6-31G |
| Energy (a.u) | -231.61 | -234.56 |
| C-C-C bond angle (°) | 120.5 | 120 |
| Fragments bond distance (A) | 2.02 | 1.97 |
| C-C bond length (A) | 1.39 | 1.41 |
| Imaginary frequency (cm-1) | -818 | -566 |
| Boat | ||
| Property | HF/3-21G | HF/6-31G |
| Energy (a.u) | -231.60 | -234.54 |
| C-C-C bond angle (°) | 121.6 | 122.3 |
| Fragments bond distance (A) | 2.14 | 2.21 |
| C-C bond length (A) | 1.38 | 1.39 |
| Imaginary frequency (cm-1) | -840 | -530 |
Results show that the change to a more comprehensive method has little effect on the geometries of the transition states, as defined by bond angles, bond lengths and inter-fragment distances.
However, there is quite a marked difference between the total relative energy of the transition structures.
Thermochemical Data
Chair TS - HF/3-21G
A. -231.47 a.u
B. -231.46 a.u
C. -231.46 a.u
D. -231.50 a.u
Chair TS - B3LYP/6-31G
A. -234.41 a.u
B. -234.41 a.u
C. -234.41 a.u
D. -234.44 a.u
Boat TS - HF/3-21G
A. -231.45 a.u
B. -231.45 a.u
C. -231.44 a.u
D. -231.48 a.u
Boat TS - B3LYP/6-31G
A. -234.40 a.u
B. -234.40 a.u
C. -234.40 a.u
D. -234.43 a.u
{Where A,B,C and D are defined as earlier}
These values correlate well with those found @ [3]
Using these values it was possible to calculate activation energies, as shown in the table below:
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.71 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.61 | 54.76 | 41.96 | 41.32 | 44.7 ± 2.0 |
Values calculated with the more advanced methodology are closer to experimental values than those calculated with the HF/3-21G level of theory.
The chair transition state has a lower activation energy than the boat transition state, in agreement with the literature [1]. This is on account of the reduced steric hindrance encountered proceeding via the chair transition state than the boat transition state.
Diels Alder Cyclo-Addition
The Diels-Alder cycloaddition occurs between a diene and a dienophile, with a wide range of molecules able to take on each role, and is an example of a pericyclic reaction. The reaction is only allowed (ie. not forbidden) if the HOMO of one reactant is able to interact with the LUMO of the other. There must be sufficient orbital overlap for the reaction to be allowed, and as such the symmetry properties of the orbitals in question must be identical.
A substituted dienophile can invoke secondary orbital effects, resulting in regioselectivity.
The simplest Diels-Alder reaction is that which occurs between ethene (the dienophile) and cis-butadiene (the diene).
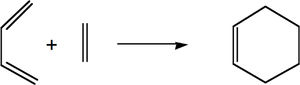
Principal orbital interactions involve the π/ π* orbitals of ethylene and the HOMO/LUMO of butadiene. It is referred to as [4s + 2s] as the diene, butadiene, has 4 π orbitals in its π system.
Ethene and cis-Butadiene
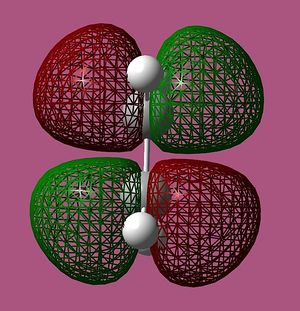
cis-Butadiene and ethene were modeled in GaussView 03, and optimised in Gaussian. The semi-empirical AM1 method was utilised and the molecular orbitals were visualised and are illustrated below:
Relative energy, and symmetry in relation to the σv plane are also indicated.
Only orbitals of identical symmetry have the required overlap density for the reaction to proceed, and so it can be seen that the HOMO of cis-butadiene can interact with the LUMO of ethene, and vice versa.
Transition States
The overlap between the two sets of pi orbitals is maximised by adopting an envelope type structure. In order to obtain the starting geometry a bicyclic system was modeled, and the -CH2-CH2- fragment removed. Inter-fragment distance was then guessed to be 2.15 A.
Optimisation was then carried out, using methodology similar to that found in Section xxx above.
One imaginary frequency was found to be -818 cm-1. This vibration is visualised below and shows synchronous bond forming, concurring with the concerted nature of pericyclic reactions.
The lowest real vibrational frequency is observed at 167 cm-1 and is attributed to the rocking of the CH2=CH2 section of the transition structure.
The energy of the transition structure was found to be -231.60 a.u.
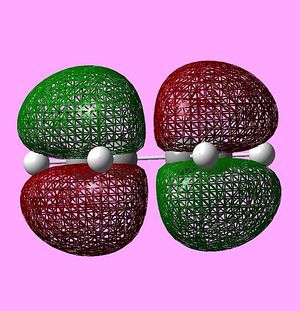
The HOMO and LUMO of the transition state were also visualised and are shown below:
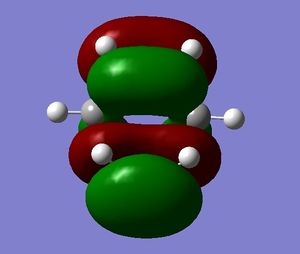

The HOMO is antisymmetric, and can be associated with overlap of the HOMO of cis-butadiene and the LUMO of ethene - where two antisymmetric molecular orbitals overlap.
Similarly, the LUMO is symmetric, and can be associated with overlap of the LUMO of cis-butadiene and the HOMO of ethene.
The geometry of the transition structure is outlined in the table below.
| Measurement | Reactants | Transition state |
| Fragment C-C Length | - | 2.21 A |
| Ethene C=C Length | 1.33 A | 1.38 A |
| Butadiene C=C Length | 1.34 A | 1.37 A |
| Butadiene C-C Length | 1.45 A | 1.39 A |
| Butadiene C-C=C Angle | 125.6° | 121.5° |
The C-C, that is only partially formed in the transition state, is markedly longer than any other bond present as a result of this. C-C and C=C bonds are no longer differentiable in the transition state, as they are in the reactants. Typical sp3 C-C bond lengths of 1.54 A [2] correlate well with the calculated C-C bond distance in butadiene. Calculated sp2 C=C bond lengths of 1.34 A and 1.33 A correlate very well with the typical values.
The Van der Waal's radius of the C atom is 1.7 A. [3]
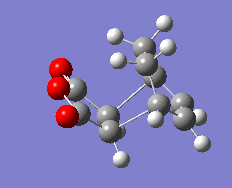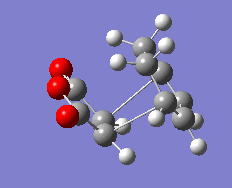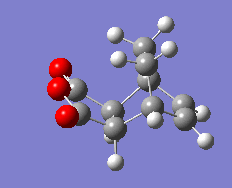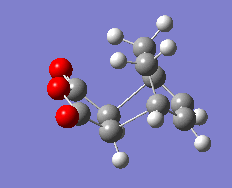
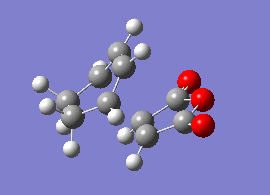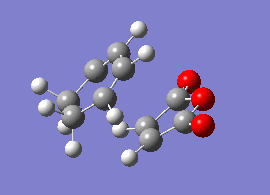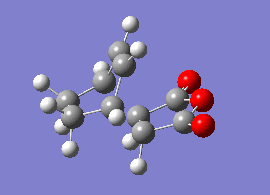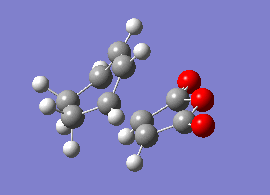
Cyclohexa-1,3-diene with Maleic Anhydride
The reaction of cyclohexa-1,3-diene and maleic anhydride yields the endo product in majority. The reaction proceeds under kinetic control so it assumed that the exo transition state is at higher energy.
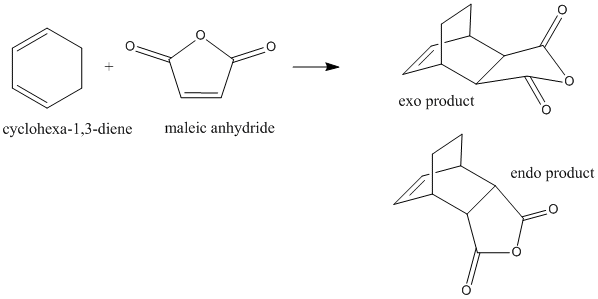
Transition States
Again, bicyclic systems were used in order to model the transition states for both the endo and exo products. 2.2 A was used as an initial guess for the inter-fragment distances, and both structures were optimised using the 'Optimisation to TS (Berny)' method, as outlined in section xxx above.
Frequency analysis was also performed.
Geometric and thermochemical properties, as well as the imaginary vibrational motions returned are displayed in the table below:
The thermochemical properties are in agreement with the prediction that the endo product will be major, the exo minor. The endo transition state has a lower transition state than the exo transition state, and as the reaction is under kinetic control, is favoured as the reaction energy barrier is smaller.
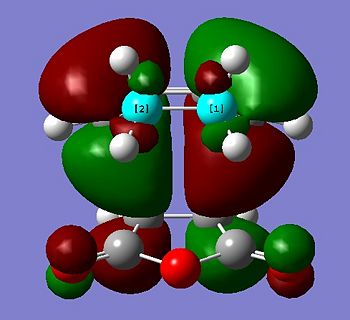
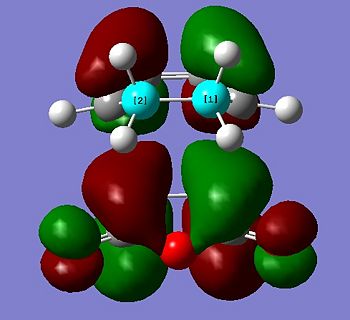
The HOMOs visualised above show differences between the endo and exo transition states, in the -(C=O)-O-(C=O)- region. The endo transition state has appreciable electron density in the region, however, the exo transition state does not. There is clearly more secondary orbital effects operating in the endo transition state, than in the exo transition state. The transition state is stabilised by these interactions, thus lowering the energy of the endo transition state relative to the exo transition state.
Conclusions
Once again, the power of computational chemistry is apparent, as is the need to balance the desired accuracy of the calculations against computational cost and time constraints. One example is when using the QST2 method which is more efficient than the QST3 method, but has the potential to fail if reactants and products are not close to the transition structure. It seems it is often worth utilising a lower level protocol initially, and if the desired results are not obtained, then a higher level calculation should be carried out.
The wide range of information gleaned from the computational methods, and close correlation with experimental results, means computational chemistry rightly deserves a place alongside more traditional methods of experimentation.
Limitations of the field are also apparent in accounting for more complex physical phenomena, such as solvent effects.
References
- ↑ Chair and boat transition states for the Cope rearrangement DOI:10.1021/ja00221a092
- ↑ H. O. Pierson, Handbook of Carbon, Graphite, Diamond and Fullerenes, 1993, p32
- ↑ Van der Waals Volumes and Radii DOI:10.1021/j100785a001