Rep:Mod:ahl10mod3
Module 3: Transition States and Reactivity
For each reaction, the reactants would need to go through a transition state before reaching the product. This transition state is characterised by the presence of maximum in the potential energy surface, where the energy difference between the transition state and reactant represents the activation energy of the reaction. For triatomics or smaller molecules, these properties are calculated through classical mechanical methods, but for larger molecules, this method would not be sufficient enough and different approach must be taken, i.e. solving the problem quantum mechanically. Using GaussView 5.0, we can find this maximum for the Cope rearrangement and Diels-Alder reaction. GaussView 5.0 uses molecular orbital-based methods to calculate this transition state by numerically solving the Schrodinger equation. The reaction pathway, location of transition state, the activation barrier energy and the structure of transition state can be obtained from one Gaussian calculation on a specific reaction.[1]
The Cope Rearrangement of 1,5-Hexadiene
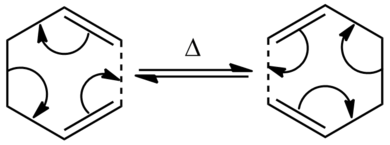
The Cope rearrangement is a intramolecular reaction involving [3,3]-sigmatropic rearrangement. This reaction is now considered to go through a concerted mechanism via either the boat conformation or the chair conformation. This rearrangement is thermally activated as the rearrangement involves 4n+2 π electrons where the stereochemistry of the reaction suprafacial and it goes via the Hückel topology.[2] By using Gaussian and GaussView 5.0, we can calculate which of the transition state conformation has a lower activation energy and with these energies obtained from the calculation, they can be compared with the experimental values to see whether they are in good agreement or not.
There are many conformations for which this molecule can be in. The conformations that we are interested in here are the ones with their relative energies to be the lowest. These conformations, when plotted on a graph against potential energies, would be represented by the minima on the plot and there are ten known conformers of 1,5-hexadiene molecule with lowest relative energies. All ten of these conformers with either gauche or anti-periplanar conformations.
Optimising the Reactants and Products

| Conformer | Point Group | Energy (Hartree) | Relative Energy (kcal/mol) |
| Gauche 1 | C2 | -231.68771616 | 3.10 |
| Gauche 2 | C1 | -231.69166702 | 0.62 |
| Gauche 3 | C1 | -231.69266121 | 0.00 |
| Gauche 4 | C2 | -231.69153032 | 0.71 |
| Gauche 5 | C1 | -231.68962573 | 1.91 |
| Gauche 6 | C1 | -231.68916016 | 2.20 |
| Anti 1 | C1 | -231.69260237 | 0.04 |
| Anti 2 | Ci | -231.69253516 | 0.08 |
| Anti 3 | C2h | -231.68907067 | 2.25 |
| Anti 4 | C1 | -231.69097054 | 1.06 |
In the table above, it contains all possible conformers of 1,5-hexadiene molecule. The gauche conformation of the molecule is where the two largest substituents are at a 60• angle to each other when viewed along the C3-C4 bond. The anit-periplanar conformation of the molecule is where instead of having the two largest substituents at 60• angle to each other, the angle is increased to 180•, where they would be opposite of each other when view along C3-C4 bond. Both conformations are illustrated in the figure above by Newman projection clearly. These two types of conformers have the lowest potential energies because they have the least steric repulsion between the two largest substituents as they are in staggered conformation where they are not overlapped on top of each other in the Newman projection. The staggered conformation has a much lower relative energy compared to eclipsed conformation as in the eclipsed conformation, the steric repulsion increases the relative energy by a large amount, making these conformers very unstable and they are rarely observed experimentally.[3]
With HF/3-21G method and basis set, it has been calculated that gauche 3 conformers have the lowest relative energy out of the ten conformers. Anti-periplanar 1 and 2 are slightly higher in terms of energy compare to gauche 3 conformer, meaning they are less stabilised compare to gauche 3. This is different to what would be expected from theory as anti-periplanar should have the lowest relative energy due to the two largest substituents being the furtherest apart and steric repulsion is at its minimum. This difference from theory can be due to the fact that a lower basis set is used here and it does not describe the molecule very well, therefore the results obtained from the calculations would not be accurate. Gauche 1 conformer has the highest relative energy compare to all the others, this is due to the steric clashing of the hydrogen atoms of the two end methyl groups of the molecule, this causes the molecule to be unstable, hence low energy of stability and therefore this would be rarely observed in reality.
For each conformer, their point group labels are different due to the orientation of the two end methyl groups of the molecule. For gauche 3, it has a point group symmetry of C1, anti-periplanar 2 has the same point group symmetry whereas anti-periplanar 2 has a point group symmetry of Ci, this implies that this molecule has an addition of centre of inversion when compared to gauche 3 and anti-periplanar 1. This suggests that anti-periplanar 2 has higher symmetry than gauche 3 and anti-periplanar 1, therefore it should have lower energy than the other two conformations, but this is not observed using 3-21G basis set and so a better method and higher basis set can be used to reoptimise these conformers to see if this changes their relative energies. A better method and a higher basis set to use would be DFT B3LYP with basis set of 6-31G(d).
| Conformer | Point Group | Energy (Hartree) | Relative Energy (kcal/mol) | Experimental relative energy[4] |
| Anti 1 | Ci | -234.61170273 | 0.06 | 0.05 |
| Anti 2 | C2 | -234.61179055 | 0.00 | 0.00 |
| Gauche 3 | C1 | -234.61132934 | 0.29 | 0.34 |
The three lowest energy conformers were being re-optimised using B3LYP/6-31G(d) basis set to obtain more accurate results from the calculations. With a higher basis set, the results from the calculations have shown that anti-periplanar 2 has the lowest energy and anti-periplanar 1 has lower energy than gauche 3. This is in agreement with theory as theory would suggests that anti-periplanar conformers would have lower energy due to less steric strain and repulsion within the molecule. From the data in the table above, gauche 3 conformers has significantly higher relative energy than previous data from HF/3-21G calculations, showing that it is less stable than anti-periplanar conformers and this also proves that B3LYP/6-31G(d) is a better method and basis set for calculating energies of the conformers. In general, the energies obtained from calculations using a higher basis set are more negative/lower than the energies calculated using the lower basis set, this is because the higher basis set can describe the molecular orbitals of the molecule better, this gives a better approximation to the molecule, therefore the calculated energies would be closer to the experimental values and from data above, the relative energies are very close to the literature values, this suggests the calculations ran through without hitting any error which would cause it to differ from the experimental values by a large amount.
The overall geometry has not varied significantly from re-optimising the conformers using a higher basis set (B3LYP/6-31G(d)). The Bond lengths and dihedral angle can be found in the table below for anti-periplanar 1, anti-periplanar 2 and gauche 3. The only significant difference is the values of the bond lengths. The C=C bond lengths for all three conformers have lengthened after the re-optimisation using higher basis set and the C-C bond lengths have shortened after optimisation using higher basis set. There is this difference can be due to the fact that the higher basis set gives a better description to the molecule orbital interactions involved in forming these bonds, therefore the bond lengths obtained from optimisation using higher basis set should be more accurate and they are in good agreement with the literature values (C-C:1.542Å, C=C: 1.333Å)[5]

| HF/3-21G | B3LYP/6-31G(d) | |||||
|---|---|---|---|---|---|---|
| C-C bond (Å) | C=C bond (Å) | Dihedral angle (•) | C-C bond (Å) | C=C bond (Å) | Dihedral angle (•) | |
| Anti 1 | 1.552 | 1.316 | 176.9 | 1.548 | 1.333 | 176.7 |
| Anti 2 | 1.553 | 1.316 | 180.0 | 1.548 | 1.334 | 180.0 |
| Gauche 3 | 1.553 | 1.316 | 67.7 | 1.550 | 1.334 | 66.3 |
By running a frequency analysis using the same method and basis set on these three conformers, we can ensure that no negative (imaginary) frequencies are obtained in this optimisation. Frequency is the second derivative of energy, so if a negative frequency is obtained, it would mean that a maximum is present in the energy plot of the molecule and this represents the transition state of molecule, hence the molecule is not optimised to a minimum. No imaginary frequencies have been obtained for all three higher basis set optimisation and so all conformers have been optimised to a minimum. We can also obtain the thermochemistry of 1,5-hexadiene from frequency analysis. The values obtained below are all more positive that the electronic energy respectively. This is because for each of the summed energies, they include extra terms which causes the molecule to be less stable and the energies are measured at standard temperature (298.15K), whereas the temperature for calculating electronic energy is at 0K. For example, sum of electronic and thermal energy takes into account of the energy of translational, rotational and vibrational energy modes and it was calculated at higher temperature, therefore there would be more kinetic movement of the molecule, so this would increase the overall energy of the molecule and hence higher than the electronic energy. For the sum of electronic and zero-point energy, it takes into account of the potential energy at 0K and the zero-point vibrational energy, hence it is the second lowest energy observed in the table below as it doesn't take into account of any thermal-related terms. The sum of electronic and thermal enthalpies takes into account of the thermal correction of RT, which is important for dissociation reaction and the sum of electronic and thermal free energy takes into account of the entropic contribution of the Gibbs free energy of the molecule, hence it has the highest value observed for all conformer as entropy terms causes the energy of a system to become less negative and therefore it is more destabilised.
| Conformer | Sum of electronic and zero-point energy(Hartree) | Sum of electronic and thermal energy(Hartree) | Sum of electronic and thermal enthalpy(Hartree) | Sum of electronic and thermal free energy(Hartree) |
| Anti 1 | -234.469295 | -234.461966 | -234.461022 | -234.500862 |
| Anti 2 | -234.469212 | -234.461856 | -234.460912 | -234.500822 |
| Gauche 3 | -234.468693 | -234.461464 | -234.460520 | -234.500105 |
Optimising the 'Chair' and 'Boat' Transition Structures

For the Cope rearrangement of 1,5-hexadiene, it can either go through the chair or boat transition state and one pathway has lower energy compare to the other. Two different methods were used to optimise the chair and boat transition states: using the redundant coordinate editor for optimising chair transition structure and the QST2 method for optimising the boat transition structure. For both methods, the basis sets used were HF/3-21G and B3LYP/6-31G(d) and the data obtained from both basis sets were compared. Anti-periplanar 2 conformer has been used as the reference for the chair and boat transition states energies to compare to. Allyl fragments, CH2CHCH2, were used for constructing the starting point for chair and boat transition structure and they were optimised to find the transition states geometry.
The allyl fragment was drawn in GaussView 5.0 and it was optimised using HF/3-21G method and basis set. This optimisation is required because it would be easier and better for later optimisations of the chair and boat transition structures, where for both chair and boat transition structures, they both are constructed using two allyl fragments.
Optimisation of Chair Transition Structure
D-space link for OPT+FREQ at 298.15K: DOI:10042/22090

The chair transiton structure of 1,5-hexadiene has C2h symmetry label and it was optimised using HF/3-21G method and basis set. The guess transition structure was consist of two allyl CH2CHC2 fragments overlapped on top of each other to form a chair structure as shown in the figure on the right. The two terminal carbon atoms of each fragment have been frozen in terms of their coordinates and an optimisation to the minimum of the structure was performed; this gives a optimised structure of chair structure. Afterwards, this optimised structure is taken to optimise to the transition structure (TS berny) with the frozen coordinates being unfrozen for the terminal carbon atoms; this give the optimised chair transition structure of 1,5-hexadiene.
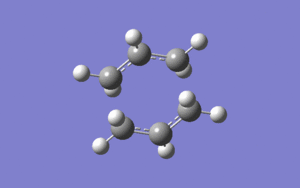
A frequency analysis was also been calculated on this optimised chair transition structure to give one imaginary (negative) frequency, which is generated by the transition state due to the frequency is equivalent of the second derivative of energy, therefore having the frequency being a negative number means that it is a maximum on the energy plot. The chair transition structure optimised by HF/3-21G was re-optimised using B3LYP/6-31G(d), which is a higher basis set than HF/3-21G. The energies obtained for this transition structure is shown below in the "Summary of energies and geometries of 1,5-hexadiene using different basis sets" table.
The calculated negative frequency is -817.99 cm-1, this negative frequency corresponds to the motion of stretching of the chair transition state structure and it is represented as a maximum on the total energy vs reaction coordinate plot as it is the transition state. The initial bond distance between the carbon terminals were set to 2.20Å before the optimisation. After the optimisation, for HF/3-21G optimisation, the bond distance has decreased to 2.020Å and the for B3LYP/6-31G(d), the bond distance has decreased to 1.969Å. These decreases in bond distance between the carbon terminals of the two allyl fragments suggest that the structure has been optimised to the transition state structure as the bond distance observed is longer than the observed bond length for C-C bond. The bond distance calculated for the either end of the terminals of the two fragments are the same, this suggests that the Cope rearrangement via the chair transition state goes through a concerted mechanism, where the breaking of one C-C bond is occurring at the same time as one C-C bond is breaking within the molecule of 1,5-hexadiene. This is further supported by the vibration of the transition structure from the negative frequency where while one partially formed σ bond is breaking, the other new bond is forming, suggesting bond breaking and forming is happening at the same time and therefore this is a concerted mechanism. The calculated bond distance using HF/3-21G is slightly longer than the bond distance calculated using B3LYP/6-31G(d) due to the fact that B3LYP/6-31G(d) is a better basis set than HF/3-21G, therefore the calculations from B3LYP/6-31G(d) level of theory would be much more accurate, the molecule would be better optimsed and the results obtained from these calculations would be preferred. This explanation applies to the electronic energy from optimisation using B3LYP/6-31G(d) as being lower than the electronic energy from optimisaton using HF/3-21G level of theory.
Optimisation of Boat Transition Structure
D-space link for OPT + FREQ of boat structure: DOI:10042/22089
The boat transition structure of 1,5-hexadiene has a symmetry label of C2v and it was optimised using HF/3-21G method and basis set. A different method was employed for the optimisation of the boat transition structure. Rather than using the frozen coordinates method used for chair transition state, the reactant and product molecule of this reaction were included in this method, the numbering of the atoms within each molecule must be correct and the geometry of the reactant and product must be set to the right geometry for this calculation to succeed because this method does not take into account that rotation about the central C-C bond is possible so if the reactant and product geometries were set up as the one shown in below:
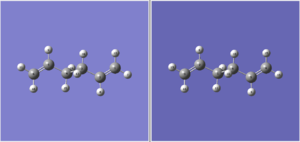
then the calculation would fail, causing the structure to optimise to a fail chair transition structure instead of boat transition. Also, the optimisation of the transistion state has been optimised to TS QST2 instead of TS berny. The starting geometry for both reactant and product need to have dihedral angle of 0• and bond angle C-C-C of 0• to allow the calculation to run without hitting any errors and fully optimise to the correct boat transition structure:

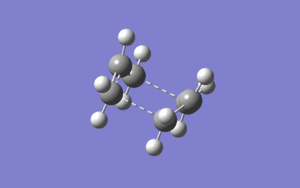
One negative frequency was obtained from the optimisation of transition structure and it has the value of -839.75 cm-1. This proves that a maximum is obtained in the total energy vs reaction coordinate plot and therefore it represents the transition state of the rearrangement. The bond distance between the terminal carbons of each fragment have shown to be the same, suggesting that it goes via a concert mechanism as the breaking and forming of the C-C bonds occur at the same time, and the vibration from the negative frequency supports this deduction from calculated results. In general, the B3LYP/6-31G(d) has proven to be a better basis set than HF/3-21G as the results obtained are better, which is the same as for the optimisation of the chair transition structure.
| HF/3-21G | B3LYP/6-31G(d) | |||||||
|---|---|---|---|---|---|---|---|---|
| Electronic Energy | Sum of Electronic and Zero-point Energy (0K) | Sum of Electronic and Thermal Energy (298.15K) | Bond distance between terminals (Å) | Electronic Energy | Sum of Electronic and Zero-point Energy (0K) | Sum of Electronic and Thermal Energy (298.15K) | Bond distance between terminals (Å) | |
| Boat TS | -231.602802 | -231.450932 | -231.445302 | 2.140 | -234.543091 | -234.402305 | -234.395995 | 2.204 |
| Chair TS | -231.619322 | -231.466699 | -231.461339 | 2.020 | -234.556985 | -234.414925 | -234.409006 | 1.969 |
| App 2 | -231.692535 | -231.539539 | -231.532566 | - | -234.611702 | -234.469212 | 234.461856 | - |
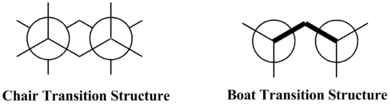
In the table above includes all the results obtained from the optimisation of the chair and boat transition structure and these data are being compared to the energy values obtained from the optimisation of anti-periplanar 2 conformer as this is the lowest energy conformer. Overall, the energy values obtained from the chair transition structure are lower than the boat transition structure. This suggests that the chair transition state is a more favoured reaction pathway for this Cope rearrangement as it has a lower energy for the chair transition state, therefore less energy is require to overcome this transition state barrier and so the molecule would go through the chair transition state for the breaking and forming of C-C bonds. When compared to the anti-periplanar 2 conformer, both transition structures have higher energy values than the conformer because the conformer is the most stable state out of the whole system. The sum of electronic and zero-point energy is lower than the sum of electronic and thermal energy, this is because the thermal energy takes into account of the energies of translational, rotational and vibrational modes at 298.15K and 1 atm, this thermal energy is much higher than the zero-point energy of the molecule, therefore it would increase electronic energy and making it a less negative value overall.
The chair transition structure has a lower energy than boat transition structure is because the bonds within the chair structure is all staggered rather than eclipsed, i.e. the bonds in the boat structure, therefore the torsional strain in boat structure is much greater than the chair structure and so this causes the electronic energy of the chair structure to be much lower than the boat structure. This staggered conformation of the chair structure and eclipsed conformation of the boat structure can be shown clearly using the Newman projection. For the Newman projection of the chair transition structure, it is shown the angle between every bond is 60•, showing that they are all staggered. For the Newman projection of the boat transition structure, the angle between the bonds is 0•, showing that they are eclipsed and hence high torsional strain.[3]
The geometry of the two transition structures are different. For the chair transition structure, the bonds are not overlapped, but for boat, the bonds are overlapped. With the distance between the terminal carbon atoms of the two fragments, the distance in boat is longer than the distance in chair, this is because in the boat structure, the torsional strain experienced causes the lengthening of this distance, but in chair structure, the torsional strain is at its minimum and therefore the distance between the carbon atom terminals is less than boat structure.
IRC for Chair and Boat Transition Structure
| HF/3-21G | B3LYP/6-31G(d) | Experimental (B3LYP/6-31G(d) | |||
|---|---|---|---|---|---|
| 0K | 298.15K | 0K | 298.15K | 0K[6] | |
| ΔE(Boat) | 50.31 | 50.20 | 37.64 | 37.64 | 44.70 +/- 2.0 |
| ΔE(Chair) | 43.93 | 45.34 | 33.67 | 33.66 | 33.50 +/- 0.5 |
The intrinsic reaction coordinate (IRC) method is used to map out the minimum energy reaction pathway for the Cope rearrangement and the basis sets used were HF/3-21G and B3LYP/6-31G(d) for the IRC through the chair and boat transition structures. This method creates series of points by taking small geometry steps in the direction where the gradient of the total energy curve is the greatest, the series of points give a guassian-shaped curve with the maximum of the curve representing the transition state of the reaction and the two plateau ends of the curve representing the energy of reactant and the energy of product. The calculations were set to take 100 points and the forward and backward IRC were calculated at the same time to give the gaussian-shaped curve. The more points the calculation is set to take, the more accurate the IRC would be but sometimes the calculation can be veered off to a completely different direction and a small bump can be observed in the total energy vs reaction coordinate plot rather than a smooth curve. IRC method is very useful as it shows that course of change in geometry for a molecule for a particular reaction and the activation energy of the reaction can be calculated. The activation energy of a reaction is the energy required for the reactant to reach its transition state, which it would subsequently lead to the formation of product, therefore in simpler terms, the activation energy is the energy difference between the energy of transition state and the energy of reactant.
As shown in the table above, it shows that the IRC calculation of the chair transition structure has significantly lower activation energy than the IRC calculation of the boat transition structure for both levels of theory used, this is because, as explained in previous section, the boat transition structure experiences more steric repulsion between the atoms due to the clashing of molecular orbitals as electrons repel each other, therefore the activation energy would be higher for boat as the reactant needs to gain more energy to reach and pass over the transition state barrier. The reaction would go via the pathway with the lowest activation energy, in the case of Cope rearrangement of 1,5-hexadiene, the chair transition structure pathway is greatly favoured as the activation energy is much lower that boat transition structure pathway and therefore the Cope rearrangement would go through the chair transition state.
The minimised structures of 1,5-hexadiene has been obtained from the IRC as the number of points set to calculate was 100 for both boat and chair IRC calculations. For the chair transition state IRC, only 89 steps present in the calculation, this suggests that the product has been minimised. The minimised conformer for the Cope rearrangement is shown to be the gauche 3 conformer for both HF/3-21G and B3LYP/6-31G(d) method. The molecule must have a gauche 3 conformation to allow the molecule to go via chair transition structure to reach to the other side of the transition state barrier and therefore the minimised structure is gauche 3. For the boat transition state IRC, 93 steps were taken in the calculation. The minimised structure for the product is syn-periplanar structure, where when observed through the Newman projection, all substituents are eclipsed with the -CHCH2CH2 substituents perfectly eclipsed on top of each other. The starting conformer must be in this conformation for the molecule to rearrangement via the boat transition structure, therefore this explains why the Cope rearrangement would prefer to go via the chair transition structure as the minimised structure of the conformer is very high in electronic energy, so it would not be stable and this geometry is rarely observed experimentally.
By changing the temperature of the reaction in the IRC calculation, a lower activation energy has been observed for temperature at 298.15K. Lower activation energies have been observed for higher temperature is because at 0K, the energy of the reactant is lower due to the fact that thermal energy is not taken into account and the rotational, translational and vibrational energies are very low, so the overall energy of the reactant would be lower than the energy at 298.15K. This lowering in the energy of the reactant means that a greater input of excess energy is needed for the reactant molecule to overcome the activation energy barrier, therefore it requires more motion of the molecule to gain more kinetic energy and hence the system is gaining energy to overcome the transition state barrier.
When comparing the calculated activation energies with the experimental values, for the chair transition state activation energy is in good agreement with the 0K experimental value, this suggests that the set-up of the calculation to this IRC was correct. For the boat transition state activation energy, the calculated activation energy is much lower than the experimental value and it is close to the chair transition state activation energy, this might be because the reaction went via a transition structure that is somewhere in between the chair and boat transition structure, therefore the activation energy is in the middle of the two experimental activation energy values.
| Total energy graph of the boat transition IRC with B3LYP/6-31G | IRC animation of boat transition state |
| Total energy graph of the chair transition IRC with B3LYP/6-31G | IRC animation of chair transition state |
The Diels Alder Cycloaddition
Cis-Butadiene
| Energy | C=C bond length | C-C bond length | C=C-C angle |
| 0.04879719 a.u. | 1.335Å | 1.449Å | 125.67• |
Cis-butadiene is an organic molecule with alkene functionality which can undergo intramolecular [2+2] cycloaddition, through the Möbius topology, to form cyclobutene under light excitation. A molecule of cis-butadiene was drawn in GaussView 5.0 and it was optimised using AM1 Semi-Empirical molecular orbital method. The method used here is considered to be a lower basis set when compared to HF/3-21G and B3LYP/6-31G(d), but it is sufficient enough to give us good approximations and results for cis-butadiene.
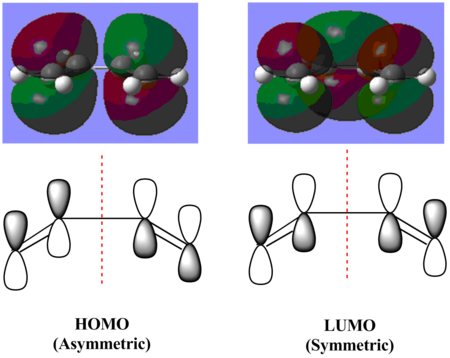
Butadiene is a diene in Diels-Alder reaction but it can only react with a dienophile if it is in the cis- conformation due to the orientation of π orbitals of the two alkene functional groups within the molecule. The MO surfaces of the HOMO and LUMO of cis-butadiene were obtained from the optimisation and a qualitative sketch of the contributing π orbitals is in the figure on the left. As shown in the figure, the red dotted line is the plane of symmetry of the cis-butadiene molecule and it shows that for the HOMO, it is asymmetric with respect to the plane of symmetry of the molecule and the LUMO, it is symmetric with respect to the plane of symmetry of the molecule. With the black lobes of the p-orbitals in the sketch representing the red-coloured electron density and the white lobes of p-orbitals representing the green-coloured electron density on the MO surfaces generated by GaussView, the sketches and MO surfaces are in good agreement with each other and they show the symmetry of the two MOs very clearly.
The HOMO has three nodal planes and the LUMO has five nodal planes. The higher the number of nodal planes in a molecular orbital, the higher it is in energy and hence more anti-bonding character in the molecular orbital. The LUMO is higher in energy due to the higher anti-bonding character. Both HOMO and LUMO are consist of π orbitals, therefore for a Diels-Alder reaction to be feasible, the dienophile must have π orbitals for its HOMO and LUMO to give the best orbital overlap with the HOMO and LUMO of cis-butadiene and therefore the product formed will be stable.
The geometry of the molecule is presented in the table below. The bond lengths for C-C bond and C=C bond are in good agreement with literature values (C-C: 1.330Å, C=C: 1.443Å)[5] and the bond angle for C=C-C is slightly wider than what would be observed in bond angle of a simple alkene, this is due to the presence of the other alkene end group, there is slight steric and electronic repulsion through space between the two alkene groups and therefore the angle is slightly wider than normal.
Butadiene & Ethylene

The Diels-Alder reaction between cis-butadiene and ethylene involves 6 π electrons, where this cycloaddition is classified as π4s + π2s with butadiene contributing 4 π electrons and ethylene contributing 2 π electrons. Both components are suprafacial and the transition state goes through the Hückel topology. This reaction is allowed due to the matching symmetry of the orbitals of butadiene and of ethylene involved in the formation of molecular orbitals for transition state, also the molecule of butadiene must be at a cis- conformation for the overlap of the π orbitals between itself and ethylene to be correct for this reaction to occur.[2]

An optimisation and frequency analysis of the butadiene fragment with ethylene fragment were performed using AM1 semi-empirical method and the initial distance between the carbon atom terminals of each fragment was set to 2.20Å. The optimisation was set to optimised to TS berny and the force constant was calculated once, this allows the guessed transition state structure of this reaction to optimise to the closest structure the method allowed. There is one negative frequency value shown from the frequency analysis and the value is -956.38 cm-1. This negative frequency value proves that a maximum has be obtained in the total energy curve and this represents the transition states. The vibration of the transition structure shows that the formation of the two new σ bonds are synchronous as the stretch of the two fragments is symmetrical, therefore this shows that the reaction goes via a concerted mechanism rather than stepwise mechanism. when compared to the positive frequency value of 246.61 cm-1, the vibration of the transition state structure shows that the stretch is asymmetrical where while one of the partially formed C-C bond is shortening, the other partially formed C-C bond is lengthening, this suggests that the formation of the C-C bonds are asynchronous and therefore there can be other potential reaction pathways, where it goes via a stepwise mechanism rather than a concerted mechanism as shown by the negative frequency.
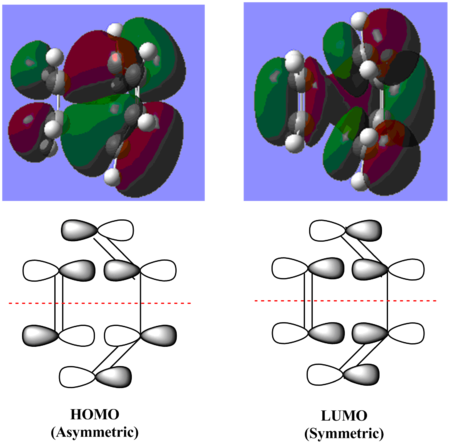
The HOMO of ethylene and LUMO of butadiene are both symmetric with respect to the plane of symmetry, therefore they interact with each other to form the LUMO of the transition state which also has a plane of symmetry. The LUMO of ethylene (Φ2) and HOMO of butadiene (ψ2) are both asymmetric with respect to the plane of symmetry, they both combine together to form the HOMO of the transition state, which is asymmetric with respect to the plane of symmetry. For both molecules, only their HOMO and LUMO can interact with each other to give the HOMO and LUMO of the transition state because all of these orbitals have molecular orbitals with the same symmetry, therefore they can combine together to form new MOs. Both of these interactions are allowed by FMO theory. This reaction is under noraml electron demand, where the HOMO of the electron-rich diene donate electron density into the LUMO of the electron-poor dienophile and hence forming the HOMO of the product cylcohexene.
The geometry of the transition state is shown in the table below. The C=C bond lengths for both butadiene and ethylene are longer than the normal C=C bond length (1.33Å)[5], the values for these two bonds are somewhere in between the length of C-C bond and C=C bond, this suggests that these bonds are lengthening as they change from π bonds to σ bonds and this is the same for C-C bond in butadiene fragment, but this bond is shortening as it changes from σ bond to π bond for this reaction. The distance between the carbon atom terminals are within the Van der Waal radius of two carbon atoms (1.70 x 2 = 3.40Å)[7], therefore the distance of the partially formed C-C bond obtained from the calculation is within the attractive region between the two carbon atoms and so the terminals are associating rather than dissociating.
| Ethylene C=C/Å | Butadiene C=C/Å | Butadiene C-C/Å | Distance between C atom terminals/Å |
| 1.383 | 1.382 | 1.398 | 2.119 |
D-space link for IRC of the Diels-Alder reaction between butadiene and ethylene: DOI:10042/22182
The reaction coordinate pathway can be animated from the IRC and it shows that the ethylene approaches the molecule of butadiene from above the plane of the butadiene molecule. This is because from the Frontier Molecular Orbital theory[8], the HOMO of ethylene interacts with LUMO of butadiene and LUMO of ethylene interacts with HOMO of butadiene, so for maximum efficiency of overlap of the π orbitals of each molecule, the ethylene molecule must approach the butadiene from either above or below the plane and therefore matching and overlapping of lobes can occur to form the HOMO and LUMO of product. As shown in the animation, the ethylene molecule approaches the molecule of butadiene at a 99• angle. The activation energy for this reaction is 23.23 kcal/mol and the Gibbs free energy to this reaction is -39.93 kcal/mol. This activation energy barrier is not very high and it is good agreement with the literature value (27.5 kcal/mol)[9]. For the Gibbs free energy, it is in good agreement with literature value (40 kcal/mol)[9] the negative sign suggests that the reaction is spontaneous and facile, also from the IRC plot, the energy of the product is lower than the energy of the reactant and this suggests that this Diels-Alder reaction is exothermic as mentioned in relevant literature.
| FMOs of butadiene and ethylene | IRC animation of Diels-Alder reaction of butadiene and ethylene | IRC energy plot of the Diels-Alder reaction between butadiene and ethylene |
Regioselectivity of the Diels Alder Reaction
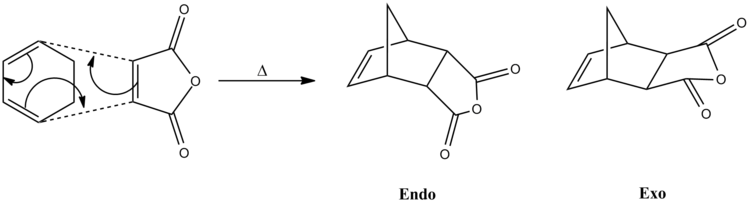
The Diels-Alder cycloaddition reaction between cyclohexadiene and maleic anhydride involves 6 п electrons, where cyclohexadiene contributes 4 п electrons and maleic anhrydide contributes 2 п electrons. This is classified as п4s + п2s cycloaddition, where both molecules have suprafacial components, hence the stereochemistry of this reaction is suprafacial and it proceeds via Hückel topology as it is thermally activated. The maleic anhydride acts as the dienophile of the cycloaddition as the carbonyl functional groups and the oxygen atom in the ring withdraw the electron density away from the double bond of the molecule, this causes the energy of the HOMO and LUMO of the dienophile to increase, therefore a better energy match between the HOMO and LUMO of the two molecules and hence the cycloaddition is more facile and the resulting HOMO is greatly stabilised and low in energy.[10]
Optimisation of the transition structure was done using previously optimised molecule of cyclohexa-1,3-diene and maleic anhydride and the frozen coordinate method was used for optimisation of transition structure. The initial distance between the carbon atom terminals of the two reactants were set to 2.20Å for the guess transition structure. The frequency analysis and IRC calculations were also been put through to GaussView 5.0. One negative frequency value has been obtained at cm-1 and this represents the transition state of the reaction. The electronic energy of the endo transition state is lower than the electronic energy of the exo transition state, this is because there is steric clash between the bridge of the molecule and the O=C-O-C=O part of the maleic anhydride in the exo form, therefore the exo structure is less stabilised and hence higher in electronic energy.
The negative frequency for endo form is observed at -805.69 cm-1 and the vibration of the negative frequency has shown that it is a symmetrical stretch of the molecule, suggesting that the formation of the two new σ bonds is synchronous and therefore this reaction goes via a concerted mechanism. For the exo form, the negative frequency is observed at -812.13 cm-1, the vibration of the molecule at this frequency is symmetrical, showing the formation of the two new σ bonds to be synchronous and therefore the mechanism is concerted as you would expect from a Diels-Alder cycloaddition reaction.
| Animation of vibration of the endo transition structure | Animation of vibration of the exo transition structure |
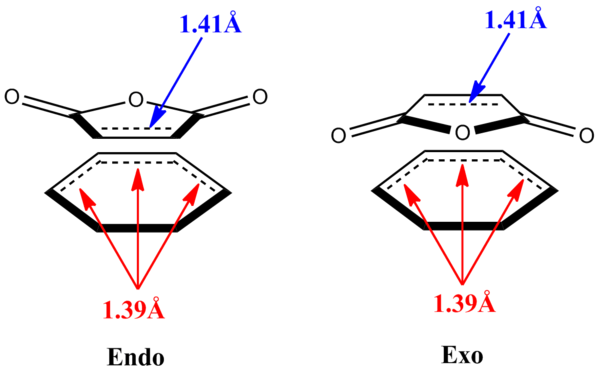
The HOMO of cyclohexadiene is combined with the LUMO of maleic anhydride, where both MOs are asymmetrical with respect to the plane of symmetry of the molecules themselves, to form the HOMO of the endo and exo transition states. As shown in the figure on the right, the symmetry of the HOMO is asymmetric. From the checkpoint file of cyclohexadiene, it shows that the HOMO is asymmetric and the LUMO is symmetric. From the checkpoint file of maleic anhydride, it shows that the HOMO is symmetric and the LUMO is asymmetric, but the HOMO can not interact with the LUMO of cyclohexadiene because the HOMO of maleic anhydride has much more negative energy compared to LUMO of cyclohexadiene, the energy gap between the two is too far apart and therefore it can not combine together to form a new molecular orbital for the product. The LUMO of the endo and exo transition structures is the anti-bonding orbital formed from the combination of HOMO of cyclohexadiene and LUMO of maleic anhydride as interaction between LUMO of cyclohexadiene and HOMO of maleic anhydride is unavailable.
There are two possible isomers for which the product can adopt: exo and endo. Formation of endo isomer is greatly preferred over formation of exo isomer is because in the endo conformation of the transition structure, it has primary and secondary interactions between the π orbitals of cyclohexadiene and maleic anhydride, whereas in exo conformation, there is only primary interaction between the π orbitals, therefore the endo conformation has higher stabilisation energy than exo conformation, lowering the activation energy barrier and so the formation of endo conformers is favoured over exo conformers. The activation energy of the endo transition state is lower than the activation energy of exo transition state due to the extra orbital interactions, this means that the rate of formation of endo product is much faster than the rate of formation for exo, making the endo product to be the kinetic product and the thermodynamic product of the reaction and the exo product being the minor product, i.e. minor product of the reaction. There are ten observable nodal planes within both HOMOs of the exo and endo form of the transition state, but the HOMO of the endo form has a much better overlap of the π orbitals than the exo form and hence lowering the overall energy.[8] There is no general rule of preference to either one of the isomer is more favoured over the other for Diels-Alder reaction, some might suggest that from the Salem-Klopman equation, it shows that endo isomer is favoured in most Diels-Alder reaction but this general area and concept is still not very well understood by chemists to present day.
For both endo and exo transition structure, they are asymmetric with respect to the plane of symmetry of the structure and the bond lengths for the transition structures are the same for both, showing that for the bonds involved in this cycloaddition, the bond lengths are somewhere between the bond lengths for C-C bond and C=C bond. This suggests that the C=C bonds are changing into C-C bonds as the bonds lengthen and the C-C bonds are changing into C=C bonds as the bonds shorten.

The exo conformer can experience more strain than the endo conformer due to the clashing of the carbonyl oxygen orbitals and the π orbitals of the cyclohexadiene molecule. There is also steric clash between the maleic anhydride C-O-C bridge and the C-C-C bridge of the the cyclohexadiene which causes the exo conformer to be more strained and this subsequently leads to the exo form having higher energy than the endo form of the product. From the result of the IRC calculations, it shows that the reaction going via endo transition state has lower activation energy than the reaction going via exo transition state, this is because the endo transition state is more stabilised when compared to exo transition state and therefore less energy require to overcome the transition state barrier. From the table below, it shows that for both transition states, the Gibbs free energies have been calculated and it shows that reaction via endo transition state has a more negative Gibbs free energy value than the exo transition state. This difference in Gibbs free energy means that the reaction going via endo transition is more facile than the reaction going via exo transition state, therefore the rate of reaction via endo transition state would be higher than the rate of reaction going via exo transition state. The negative on the Gibbs free energy values suggests that reactions are spontaneous and reversible and it also shows that endo is the thermodynamically stable product. From the IRC energy plot, it has shown that the energy of the reactant is higher than the energy of the product, meaning that the reaction is exothermic as the change in enthalpy is negative, therefore excess energy is dissipated to allow the product to have a lower energy state than the reactant.
For the IRC plot of the reaction going via exo transition state, the plot is reversed where it shows the dissociation of the exo product back to the two reactants. The set up to the calculation is the same as the set up for the endo calculation, this difference can be induced by Gaussian itself where it assumes that the exo product is less stable and dissociation of the exo product is more favoured than the formation of it, so then the resulting reactants can go via the endo transition state instead to form the endo product which is more stable.
D-space links for IRC of Endo and Exo transition state: DOI:10042/22131 DOI:10042/22130
| Transition State | Electronic energy (hartree) | Activation Energy (kcal/mol) | Gibbs Free Energy (kcal/mol) |
| Endo | -0.05181746 | 26.67 | -41.51 |
| Exo | -0.05041985 | 28.21 | -40.49 |
| IRC total energy plot for the reaction via endo transition state | IRC animation of Diels-Alder reaction via endo transition state |
| IRC total energy plot for the reaction via exo transition state | IRC animation of Diels-Alder reaction via exo transition state |
Conclusion
To conclude, the lowest energy conformer using HF/3-21G method is gauche 3, but this method and basis set is not very good when compared to B3LYP/6-31G(d), which is a higher basis set method. The calculations using higher basis set have shown that the lowest energy conformer is anti-periplanr 2, this is what would be expected as anti-periplanar conformers have bigger dihedral angle, therefore less torsional strain and steric clashes and hence should have the lowest energy. For the chair and boat transition structures, the chair TS has shown to be the more stable structure for the Cope rearrangement as the boat structure leads to formation of the syn-periplanar conformer, which is highly disfavoured and therefore the activation energy and Gibbs free energies are lower for chair transition state.
For the butadiene and ethylene Diels-Alder reaction, it has shown that the reaction goes through Huckel topology and using the FMO theory, the combination of the HOMO of butadiene and LUMO of ethylene gave the HOMO of the Diels-Alder product which is cyclohexene. The vibration of the transition state has proven this reaction is in fact a Diels-Alder reaction by having synchronous formation of the new C-C bonds, meaning that the reaction goes via a concerted mechanism. The Diels-Alder reaction between maleic anhydride and cyclohexadiene has shown to favour the formation of endo isomer as the Gibbs free energy activation energy has suggested that it is the kinetic and thermodynamic product of the reaction due to the presence of secondary orbital overlap effect for the endo transition state. Also, exo is less stable due to the clashing of the bridge of cyclohexadiene and O=C-O-C=O of the maleic anhydride, this causes the exo transition sttate to be more unstable than the endo transition state.
Notes
Please click into some of the figures on this wiki page for animations of the motion of the molecule to be activated.
References
- ↑ M. Bearpark, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3. Last date accessed: 07/12/2012.
- ↑ 2.0 2.1 H. Rzepa, Pericyclic Reactions, 2nd year Imperial College London lecture course, 2012.
- ↑ 3.0 3.1 H. Rzepa, Conformational Analysis, 2nd year Imperial College London lecture course, 2012.
- ↑ B. W. Gung, Z. Zhu and R. A. Fouch, J. Am. Chem. Soc., 1995, 117, 1783-1788.
- ↑ 5.0 5.1 5.2 F. H. Allen, O. kennard and D. G. Watson, J. Chem. Soc. Perkin Trans., 1987, II, S7-S8.
- ↑ O. Wiest, K. A. Black and K. N. Houk, J. Am. Chem Soc., 1994, 116, 10336-10337.
- ↑ R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 18, 7384-7391.
- ↑ 8.0 8.1 K. N. Houk, Acc. Chem. Res., 1975, 8, 11, 361-369.
- ↑ 9.0 9.1 E. Goldstein, B. Beno and K. N. Houk, J. Am. Chem. Soc., 1996, 118, 6036-6043.
- ↑ A. Spivey, Heteroaromatics, 2nd year Imperial College London lecture course, 2012.