Rep:Mod:ahfosiuafhsodifhoisopdsjfo

Physical Module

Cope Rearrangement

Introduction

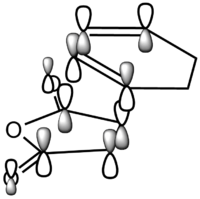
1,5-hexadiene can undergo a [3,3] sigmatropic rearrangement according to the mechanism shown on Figure 1. It is known that this reaction proceeds via a chair or boat transition state(TS). The structures, energies and vibrational patterns of the transition states were computed to investigate the nature of the transition states. Also, the activation energies (E_a) corresponding to chair and boat transition states were calculated to decide which transition state is favoured.

Figure 1: Mechanism of Cope Rearrangement

Optimisations of Reactants and Products

In this section, different conformers produced by the rotation about the central σ C-C bond for 1,5-hexadiene were investigated. Starting from a molecule of 1,5-hexadiene with an approximate anti or gauch linkage of the central carbon atoms, different conformers can be computed using HF/3-21G method, followed by optimisations using B3LYP/6-31G* method. The results were summarised in the following table.

Table 1: Results for Optimisations and Frequency Analysis

Conformer	Anti-1	Anti-2	Gauch-3	Gauch-5
Structure (HF/3-21G)	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene
Energy/Hartrees	-231.6926024	-231.6925353	-231.6926612	-231.6896158
Relative Energy to Gauch 3 (kCal/mol)	0.04	0.08	0.00	1.91
Structure (B3LYP/6-31G*)	Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene
Energy/Hartrees	-234.6118004	-234.6117104	-234.6113293	-234.6091105
Relative Energy to Gauch 3 (kCal/mol)	-0.30	-0.24	0.00	1.39
The Sum of Electronic and Zero-Point Energies at 0 K (Hartrees)	-234.469306	-234.469204	-234.468693	-234.466402
The Sum of Electronic and Thermal Energies at 298.15 K (Hartrees)	-234.461974	-234.461857	-234.461464	-234.459234
Point Group	C2	Ci	C1	C1
Newman Projection along Central Carbons
Log File	File:Lx-Anti- 6-31g.log File:LxAnti1 6-31gfreq.log	File:LxAnti26-31g.log File:LxAnti26-31gfreq.log	File:LxGauch3 6-31g.log File:LXGAUCH3 6-31GFREQ1.LOG	File:LxGauch 5 6-31g.log File:LxGauch 5 6-31gfreq.log

Each optimisation was judged to be finished by looking at the log flie to check the convergence of all of the forces and displacements and comparing the electronic energies with those listed in Appendix A in the main Wiki page. The frequency analysis can be checked by looking at at low frequencies to check whether these frequencies lie within the range of ±15 cm^-1 and the absence of imaginary frequencies to ensure a minimum is reached.

From the optimised structures in Table 1, it can be concluded that the similar structures for a conformer were obtained in both HF/3-21G and B3LYP/6-31G optimisations. Also, all of the central C-C bond lengths calculated by different methods are almost the same up to 3 significant figures as labelled in Table 1, suggesting the bond lengths are insensitive to the two different methods used in optimisations and the relative orientation of two C=C bonds.

The angles measured on the optimised structures for the same conformer show a certain degree of deviation between HF/3-21G and B3LYP/6-31G* optimisations. For a given conformer, B3LYP/6-31G* method always produces a larger angle than HF/3-21G method by about 1.5^o.

In terms of relative energy of the conformers, the Gauch-3 conformer is the most stable and gauch-conformers are more stable than anti-conformers in HF/3-21G method. However, this order is changed in B3LYP/6-31G method, in which Anti-1 is the most stable and anti-conformers are more stable. The reason is the HF/3-21G method, which is simpler than B3LYP/6-31G* method, excludes the electronic correlation. In contrast, B3LYP/6-31G* method includes the electronic correlation. Consequently, the stabilisation effect caused by σ_C-C→π* interaction, which is overlooked by HF/3-21G method, favours the gauch-conformers.

According to relative energy for the B3LYP/6-31G optimisations, the anti-conformers are more stable than gauch-conformers. In addition to the effect of σ_C-C→π* interaction as stated above, this is possibly due to the longer distance between two propenyl groups for anti-conformers in comparison to gauch-conformers, resulting in the less steric strain, deduced from the Newman projections shown in Table 1. The Anti-1 conformer is more stable than Anti-2. Because the two propenyl groups orient in the same direction in Anti-1 as shown in the Newman projection, which facilitates the stabilisation of π→π* between two propenyl groups. This effect is less pronounced for Anti-2, where the orientation for these two groups is opposite as shown on the optimised structure.

Optimisations of Chair and Boat Transition States

The chair TS was optimised in two different ways, normal optimisation and frozen coordinate method, based on the -CH₂-CH-CH₂ fragment. The boat TS was optimised based on the structure of Anti-2 conformer of 1,5-hexadiene. All of the TS structures were optimised by HF/3-21G initially, followed by B3LYP/6-31G*.

Figure 2: Chair TS and Boat TS

Table 2: Results for Optimisations and Frequency Analysis for Transition States

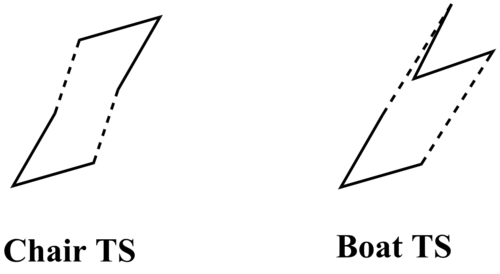
	Method	Structure	Lengths Between Terminal Ends (Å)	C-C Bond Lengths Inside the Fragment (Å)	Sum of Electronic Energy and Zero-Point Energies at 0 K (a.u.)	Sum of Electronic and Thermal Energies at 298.15 K (a.u.)	Imaginary Frequency (cm-1)	Point Group	Log Files
Chair TS (Normal)	TS(Berney), HF/3-21G		2.02	1.39	-231.466701	-231.461341	-817.96	C2h	File:Lx-chair-ts-hf3-21g.log
	TS(Berney), B3LYP/6-31G*		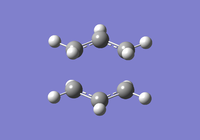1.97	1.41	-234.414929	-234.409009	-565.54	C2h	File:Lx-chair-ts-hf3-21g-6-31g.log
Chair TS (Frozen)	TS(Berney), HF/3-21G		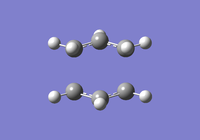2.02	1.39	-231.466705	-231.461345	-817.89	C2h	File:Lx-chair-ts-fr-step2.log File:LX-CHAIR-TS-FR-STEP2-FREQ.LOG
	TS(Berney), B3LYP/6-31G*		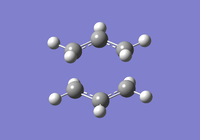1.97	1.41	-234.414929	-234.409009	-565.54	C2h	File:Lx-chair-ts-fr-step2-6-31g.log
Boat TS	TS(QST 2), HF/3-21G		2.14	1.38	-231.450926	-231.445298	-840.02	C2v	File:Lx-boat-qst2.log
	TS(QST 2), B3LYP/6-31G*		2.21	1.39	-234.402342	-234.396008	-530.36	C2v	File:Lx-boat-qst2-6-31g.log

After each optimisation and frequency analysis, the presence of an imaginary frequency as shown on Table 2, which is negative, verifies a transition state is reached.

From Table 2, the chair TS is more stable than the boat TS, indicated by the more negative energies for each given calculation method. This is due to the staggered conformation of two allyl fragments in the chair transition state, causing less steric strain compared to the boat transition state where two allyl fragments are eclipsed to each other.

The lengths between terminal ends are larger for boat TS than for chair TS, resulting from the larger steric strain, making two fragments further from each other. Also, the lengths are sensitive to the calculation methods and basis sets. The HF/3-21G method produces a shorter length for chair transition state but a longer length for boat transition state. All of the lengths are shorter than the Van der Waals radius (3.40 Å) between two sp² carbons, but longer than the covalent radius(1.46 Å), suggesting the bonds are being formed between two terminal ends. In addition, the C-C lengths within each fragment are the same for each transition state and slightly shorter than the the covalent radius(1.46 Å) . This reveals that all of C-C bonds have double bond character and hence π electrons are delocalised within each gragment. So the identity of transition states can be verified in terms of bond lengths.

During optimisations of chair transition states, two different ways were employed as mentioned above. In the end, same energies and bond lengths were obtained, suggesting the structure of chair transitions states can be predicted successfully by both of the ways.

To investigate how the new bonds are formed during the rearrangement, the vibrational patterns corresponding to the imaginary frequencies for chair TS and boat TS were summarised as follows.

Figure 3: Vibration of Chair Transition State

Figure 4: Vibration of Boat Transition State

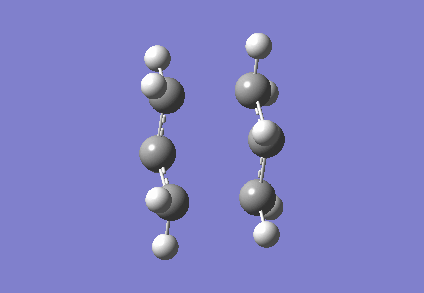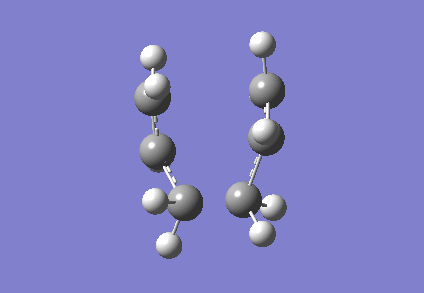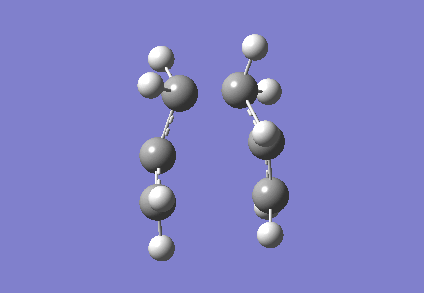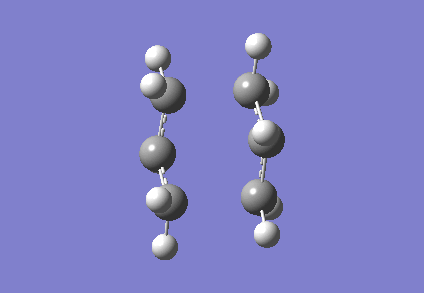
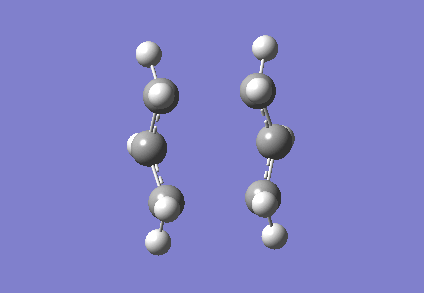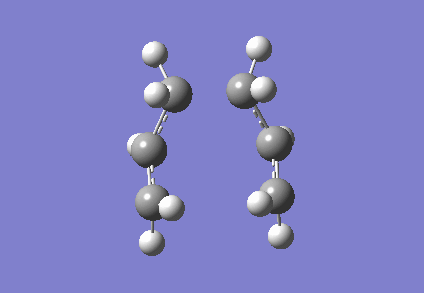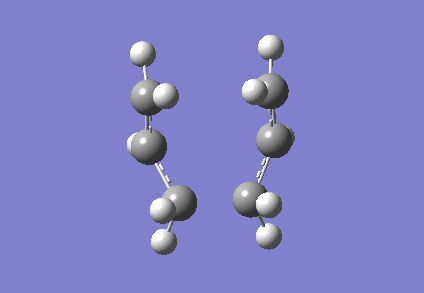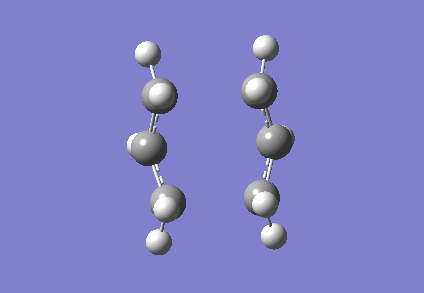
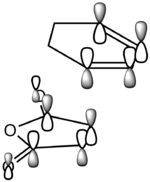
It is clear from Figures 3 and 4 that the chair TS and boat TS vibrate in a similar fashion. The two carbons on the same end of the allyl fragments move concertedly towards each other to form a new σ C-C bond. This forces the other two carbons on another terminal move away from each other and the σ C-C bond is broken.

Finding the Conformer from the Transition State

To find the conformer corresponding to the transition state, it is necessary to undergo an Intrinsic Reaction Coordinate (IRC) Analysis. Starting from the optimised structure of the chair TS by HF/3-21G , the minimum was approached step by step along the reaction coordinate in the forward direction. The results were summarised in the following table.

Table 3: Results for IRC Analysis

	Initial IRC	Further IRC
Electronic Energy (a.u.)	-231.6915789	-231.691667
Dihedral Angle	67.2o	64.2o
Point Group	C2	C2
Structure	Pentahelicene	Pentahelicene
IRC Path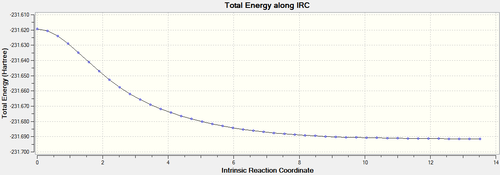
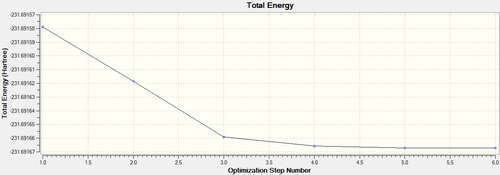
Log File	File:Lx-chair-ts-hf31g-irc.log	File:Lx-chair-ts-hf31g-irc-method1.log

From Table 3, the initial IRC calculation produces a conformer that does not correspond to any of the molecule listed in Appendix A on the main Wiki page, although the IRC path is almost flat in the end as shown on Table 3. This shows that the point for transition state was not reached. To solve this problem, the last point on the IRC path was taken to run a normal optimisation by HF/3-21G to proceed further along the IRC path. The path for this optimisation shows that the total energy still decreases with the optimisation progressing, confirming that the last point on the IRC path is not actually a minimum. The electronic energy for the last point on the further optimisation is the same as the Gauch-2 isomer according to Appendix A, suggesting a minimum was reached, which can also be deduced from the constant energy after the step 5 on the IRC path. Moreover, the dihedral angle among the central four carbons changes for the two conformations presented in Table 3, denoting the energy decreases with the dihedral angle between these two conformations. Overall, it is clear that the chair TS connects to the Gauch-2 conformer.

Analysis of Activation Energies

To calculate the activation energies (E_a) of the Cope Rearrangement, the following table was established. The E_a were calculated based on the Anti-2 conformer. At 0 K, E_a can be calculated from the sum of electronic energies and zero-point energy, and the sum of electronic and thermal energies at 298.15 K were used to calculate the E_a at 298.15 K.

Table 4: Results for Activation Energies (kCal/mol)

	Experimental Ea at 0 K	HF/3-21G (0 K)	Percentage Difference (%)	B3LYP/6-31G* (0 K)	Percentage Difference (%)	HF/3-21G (298.15 K)	B3LYP/6-31G* (298.15 K)
Chair	33.5±0.5	45.71	36.44	34.06	1.66	44.69	33.16
Boat	44.7±2.0	55.61	24.40	41.96	6.14	54.76	41.32

It can be deduced from Table 4 that B3LYP/6-31G* method produces closer E_a relative to experimental values at 0 K, indicated by the smaller values of percentage difference relative to experimental values. Consequently, B3LYP/6-31G* method is reliable enough to predict E_a for the Cope Rearrangement as the percentage differences are very small. In contrast, HF/3-21G is unreliable to predict E_a, indicated by the percentage differences of more than 20% as shown in Table 4. The E_a for chair TS is lower than the boat TS, due to the more stable chair TS. The boat TS is more unstable than chair TS by about 8 kCal/mol at 298.15 K. So the Cope Rearrangement favours the chair TS as it is lower in energy than boat TS at 298.15 K due to the exponential correlation between the E_a and the rate constant.

The Diels Alder Cycloaddition

Introduction

The Diels-Alder Cycloaddition, a subclass of pericyclic reaction, in which two σ bonds are formed between two ends of conjugated π-systems, namely a diene and a dienophile. Totally 6 π-electrons are involved. If diene and dienophile are substituted, two types of transition state, endo and exo, can happen in the reaction. Whether or not the reaction can happen is dependent upon the HOMO and LUMO interaction between the diene and the dienophile. If the HOMO and LUMO are similar in energy and have the same symmetry, the reaction can proceed in a concerted and stereospecific way. In this section, the nature of the transition states for this reaction was investigated through two classical reactions shown in Figures 5 and 6.

Figure 5: Mechanism 1

Figure 6: Mechanism 2

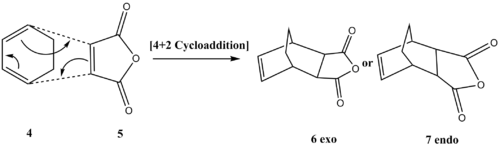
Diels Alder Cycloaddition between 1,3 Cis-Butadiene and Ethylene

Optimisation and Analysis of 1,3 Cis-Butadiene

A molecule of 1 was created using Gaussview, followed by optimisations using semi-empirical/AM1 and B3LYP/6-31G* methods. The results were summarised as follows.

Table 4: Results for Optimisation of 1,3 Cis-Butadiene

	Semi-empirical/AM1	B3LYP/6-31G*
Optimised Structure	Pentahelicene	Pentahelicene
Energy (a.u.)	0.04879719	-155.9859495
Point Group	C2v	C2v
Log Files	File:LXCISBUTADIENEOPT1.LOG File:LXCISBUTADIENEOPT1-FREQ.LOG	File:LXCISBUTADIENEOPT1-6-31G.LOG File:LXCISBUTADIENEOPT1-6-31G-FREQ.LOG
MO	Structure	Symmetry
HOMO		Antisymmetric
LUMO		Symmetric

Optimisation and Analysis of the Transition State

First of all, The lengths between terminal ends of the reactants in the TS was guessed to be 2.20 Å. Then, the TS for the Diels Alder reaction shown in Figure 5 was optimised using Semi-empirical/AM1 method, followed by B3LYP/6-31G* method. Then the HOMO and LUMO of the transition state were plotted to investigate how the frontier orbitals between the reactants interact in the TS in terms of symmetry and orbital overlap. In order to make the picture of the MOs more clearly, the resulting HOMO and LUMO were deconstructed into LCAO-HOMO and LCAO-LUMO using the theory of linear combination of atomic orbitals(LCAO). The results were presented in the following table.

Table 5: Results for the Optimisation of the TS

	Semi-empirical/AM1	B3LYP/6-31G*
Optimised Structure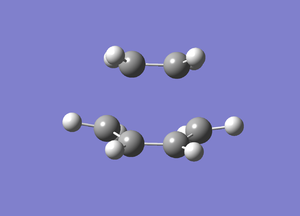
Lengths between Terminal Ends (Å)	2.12	2.27
Energy (a.u.)	0.11165468	-234.5438965
Point Group	Cs	Cs
Imaginary Frequency (cm-1)	-956.77	-525.07
Log Files	File:LXDLTS-GUESS2.LOG	File:LXDLTS-GUESS2-6-31G.LOG
MO	Structure	Symmetry
HOMO		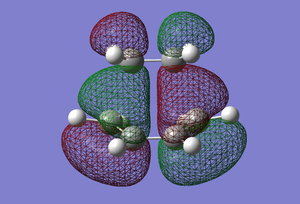Antisymmetric
LCAO-HOMO		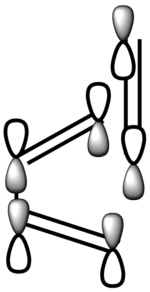Antisymmetric
LUMO		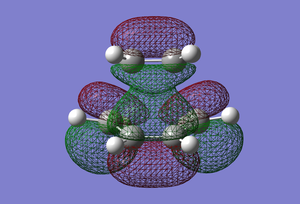Symmetric
LCAO-LUMO		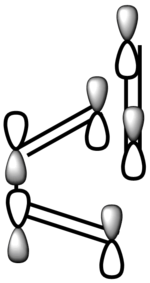Symmetric

It is clear from Table 5 that the bond lengths between partly formed C-C σ bonds are shorter than the van der Waals radius between two sp² carbon atoms (3.40 Å) but longer than the covalent between two sp² carbons (1.46 Å), suggesting C-C σ bonds are being formed, verifying the successful prediction of the transition state.

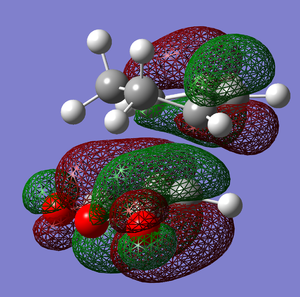
In terms of MO theory, the HOMO of the TS is antisymmetric with respect to the plane, formed from the HOMO of butadiene and the π* of the ethylene which are both antisymmetric. This can be deduced from the LCAO-HOMO presented in Table 5. So, these two frontier orbitals are allowed to overlap to form the TS. In addition, there is a significant electron density in the region where the two new σ C-C bonds are formed as shown on the image of the HOMO in Table 5. Therefore, this reaction is allowed.

To investigate how the new bonds are formed, the vibration corresponding to the TS at Semi-empirical/AM1 level was animated as follows.

Figure 7: Vibrational Motion for the TS

From Figure 7, ethylene and butadiene approach each other in a concerted fashion to form new bonds between their terminal ends. So the bonds are formed synchronously. The lowest real mode at Semi-empirical/AM1 level, as shown below, only involves the bending motion of the two reactants at 147.24 cm^-1. In contrast, the vibrational mode corresponding to the TS involves the stretching motions of the two reactants to form new bonds, which is higher in energy, reflected in the greater magnitude of the vibrational frequency.

Figure 8: Vibrational Motion for the Lowest Real Mode

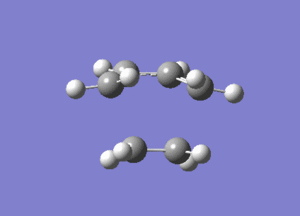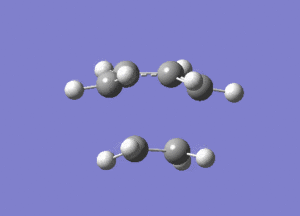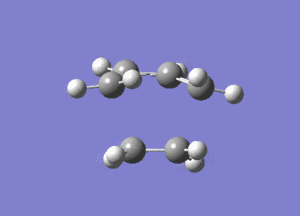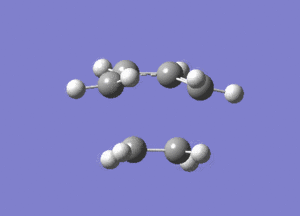
Diels Alder Cycloaddition between Maleic Anhydride and Cyclohexadiene

Optimisation and Analysis of The Exo and Endo Transition States

Before the optimisation of exo, the lengths for the partially formed σ C-C bonds (lengths a and b as shown in the Table 6) were guessed to be 2.30 Å. Two possible transition states, exo and endo were optimised analysed using the same method and procedure as described above. The results were presented in the following table.

Table 6: Results for the Optimisation of the TS

EXO	Semi-empirical/AM1	B3LYP/6-31G*
Optimised Structure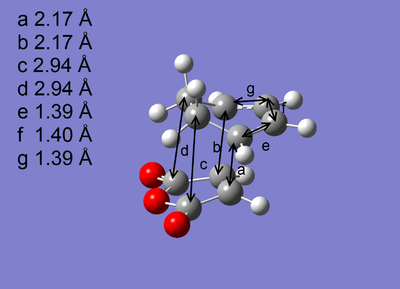
Energy (a.u.)	-0.05041979	-612.679311
Imaginary Frequency (cm-1)	-811.90	-448.45
Point Group	Cs	Cs
Log Files	File:LXTS-INITIALGUESSDA2.LOG	DOI:10042/26662
ENDO	Semi-empirical/AM1	B3LYP/6-31G*
Optimised Structure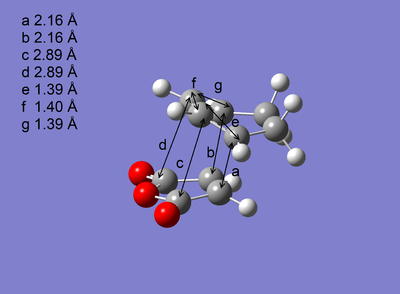
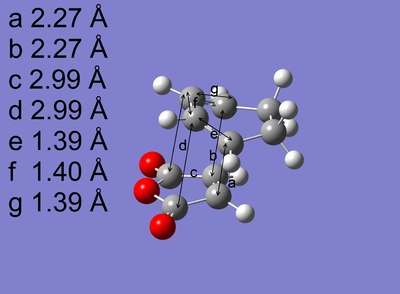
Energy (a.u.)	-0.05150477	-612.6833968
Relative Energy to EXO (kCal/mol)	-0.68	-2.56
Imaginary Frequency (cm-1)	-805.93	-446.80
Point Group	Cs	Cs
Log Files	File:LX-ENDO-GUESS.LOG	DOI:10042/26673

The transition states were successfully optimised as the distances a and b, which represent the partly formed C-C σ bonds, are exactly the same. In addition, the presence of imaginary frequency for each optimised structure reveals a maximum in energy is reached. Arrieta et al reported that the distances a and b are 2.24 Å for exo and 2.22 Å for endo, which were also calculated by B3LYP/6-31G* , agreeing both of the magnitude and the order of the distances a and b shown in Table 6.

As shown in Table 6, Exo and Endo differ in the relative orientation between the diene and dienophile. In exo, the -CH₂-CH₂- fragment of cyclohexadiene is in the same side with the anhydride group. However, this is reversed in endo where these two fragments are in the opposite side and the anhydride group is in the same side with the -CH=CH- fragment which is less bulky, causing the less steric repulsion compared to exo. Consequently, exo is more strically hindered than endo. This can also be deduced from the through space distances c and d labelled on the optimised structures, reflecting the balance between the steric hindrance which increases the distance and the extent of orbital interactions which decreases the distance, are greater for exo than for endo. The distances a and b are very similar for the endo and the exo. So its contribution to the difference in steric repulsion can be neglected.

It can be concluded from Table 6 that the exo is disfavoured sterically, due to the reasons stated above.

Table 7: Results for MO Analysis

	EXO		ENDO
MO	Structure	Symmetry	Structure	Symmetry
HOMO		Antisymmetric		Antisymmetric
LCAO-HOMO		Antisymmetric		Antisymmetric
LUMO		Antisymmetric		Antisymmetric
LCAO-LUMO		Antisymmetric		Antisymmetric

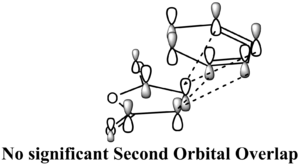
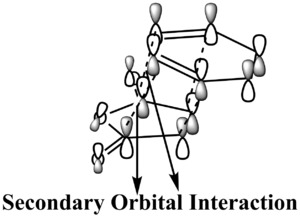
According to Table 7, the HOMOs of endo and exo are both stabilised by the primary bonding interaction between the HOMO of the hexadiene and the LUMO of the maleic anhydride. To figure out why the energy of endo is lower from the perspective of MO, it is necessary to employ the concept of Second Orbital Overlap, which means the bonding interaction of frontier orbitals between the atoms that are not involved in the σ-bond formation as suggested by Fox et al. For the endo, there are significant secondary orbital overlaps as labelled on the graph of LCAO-HOMO. In the exo, no significant secondary overlap was found due to the opposite orientation between =CH-CH= and -(C=O)-(C=O)-. So the endo should be lower in energy due to the effect of Secondary Orbital Overlap. It can be seen from above that the Secondary Orbital Overlap is an important tool to determine the relative energy between exo and endo.

In summary, the endo TS is both energetically favoured by both the steric effect and the Secondary Orbital Overlap.

To verify whether the bond formation process for this reaction is synchronously or not, the vibration of the endo was animated.

Figure 9: Vibrational Motion for the Endo TS

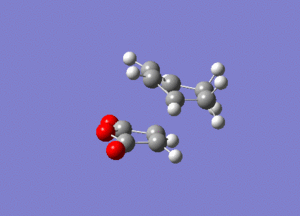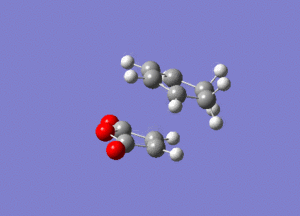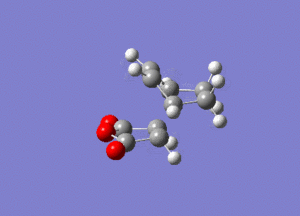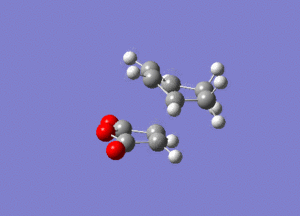
A similar vibrational pattern was obtained compared to the vibrational pattern for the Diels Alder reaction between ethylene and butadiene. Based on the animation above, it can be concluded that the bond formation is also synchronous.

Effect Neglected in AM1 Calculation

AM1 method, which is an empirical method, ignoring the effect of differential diatomic overlap. So this effect is neglected in AM1 calculation. To get over this problem, a more advanced method B3LYP/6-31G*, which involves the effect of polarisation, was employed to further optimise the structures of transition states to give more sensible results.

Conclusion

To conclude, the general strategy used in optimisations of transition states in this experiment, which is an initial optimisation using Semi-empirical/AF1 followed by B3LYP/6-31G*, is quite reliable to produce resonable results. In rationalising the relative energy of the exo TS and the endo TS, Secondary Orbital Overlap is an important tool in addition to the evaluation of steric effects and the overlaps of primary frontier orbitals. Overall, the nature of the transition states for the Diels Alder cycloadditon shown in Figures 5 and 6 can be successfully predicted by computational methods.