Rep:Mod:aed12

Introduction

Gaussview is the interface system for the Gaussian program, an electronic structure system that allows us to use computational methods to calculate predicted values for many molecular properties such as structures and energies of both molecules and their transition states, vibrational frequencies, and atomic charges to name but a few. The first section of this wiki will be dedicated to calculating some of the molecular properties of EX3 molecules and will introduce some of the methods used to predict the aforementioned molecular properties.

Optimisation of EX₃ Molecules

The first calculation made using the software is the optimisation of a molecule, in this case BH₃. The optimisation is comprised of two parts, the SCF part of the process that solves the Schrödinger equation for the electrons in the system based on a set of nuclear positions for the molecule. After this the OPT section of the calculation is performed where the nuclear positions are altered. The SCF part of the equation is repeated for each position until the lowest energy geometry is found.

For each calculation both the method of performing the calculation and the basis set of orbitals used in the calculation. These decide the assumptions made in solving the Schrodinger equation and the accuracy of the calculation. For every calculation we do the basis set and method are listed in the heading before the results of said calculation, to prevent the calculations being needlessly long we only use a moderately accurate basis set for these calculations.

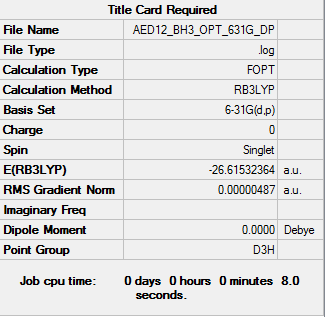
BH₃ Optimisation

B3LYP/3-21G level

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000350 0.001800 YES RMS Displacement 0.000229 0.001200 YES Predicted change in Energy=-4.546985D-08 Optimization completed. -- Stationary point found.	Optimised BH3 Molecule

B3LYP/6-31G(d,p) level

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000039 0.001800 YES RMS Displacement 0.000025 0.001200 YES Predicted change in Energy=-5.631660D-10 Optimization completed.	Optimised BH3 Molecule

The two sets of data above show optimisations of the BH3 molecule performed using the same method (B3LYP) but a progressing greater accuracy basis set. The 3-21g basis set was used in the first calculation and the 6-31g(d,p) in the second. The two methods produce different energy values for the molecule, however as these have not been performed using the same method and basis set, a direct comparison cannot be made between two so this energy difference is meaningless between the optimisations.

BBr₃ Optimisation

B3LYP/6-31G(d,p)LANL2DZ level

Optimisation log file: DOI:10042/143659

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES Predicted change in Energy=-4.088549D-10 Optimization completed.	Optimised BBr3 Molecule

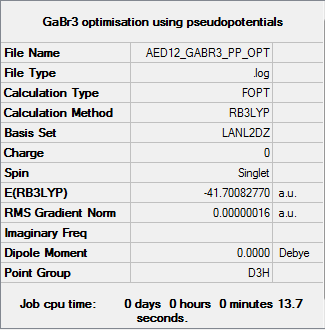
GaBr₃ Optimisation

Pseudopotentials

For the heavier Ga molecule, psuedopotentials are used. These serve to model the larger atoms with everything but their valence electrons replaced with an effective core potential which acts to simplify the wavefunction that needs to be computed. As with calculations before, these approximations are made to make the calculations we need to run simpler and faster.

B3LYP/LANL2DZ level

Optimisation log file DOI:10042/143658

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307972D-12 Optimization completed.	Optimised GaBr3 Molecule

Structure Comparison

Geometry Data

	BH3	BBr3	GaBr3
r(E-X) (Å)	1.19	1.93	2.35
θ(X-E-X) Deg (°)	120.0	120.0	120.0

The optimum bond length between two atoms is decided on a balance between two factors, there is the attractive electrostatic force that creates the bond, bringing the atoms together, and the electrostatic repulsion between the two positively charged nuclei creating the distance between them. When comparing the calculated bond lengths and angles of the three molecules optimised above, it’s clear to see that both changing the central element and changing the ligand have profound effects on the resulting bond length with no change in the bond angle.

Going from BH₃ to BBr₃ the bond length jumps from 1.19 to 1.93Å. This increase in bond length when changing ligand can be rationalised when examining the structures of the two ligands and how the structures influence the two factors previously mentioned that decide bond length. Hydrogen is the smallest of all the elements and possess just one electron that is tightly held in the very compact 1s orbital. Br on the other hand has an atomic number of 35, and its valence electrons used for the bond in question are held in the relatively much more diffuse 2p orbital. Each ligand only requires one additional electron from the boron atom to complete its octet and so in that regard, the force bringing them together to form the bond is not dissimilar, however in order for the very compact 1s orbital to overlap with the boron orbitals it much approach much closer than the large diffuse Br orbitals. They also differ in the repulsive force that each pair experiences. The increasing nuclear charge from H to Br means that the repulsive force experienced in the B-Br bond will be much larger, pushing the equilibrium bond length to a greater distance, as observed in the computed bond lengths.

When moving from BBr₃ to GaBr₃ the argument for increased bond length is also concerned with the size of the atoms. Boron is a second row element compared to the fourth row Gallium and consequently gallium has a much larger atomic radius and nuclear charge. Bromine cannot approach the highly charged gallium as closely as the lesser charged boron nor does it need to as gallium’s 4p orbitals much more diffuse than boron’s 2p orbitals. It is for this reason that we see the bond length increase from 1.93 to 2.35Å

Questions

What is a bond?

A chemical bond is the force joining two atoms or molecules in a compound. It results from an overall attractive force between them which is caused by the electrostatic interactions between the atoms or molecules. A bond gives the compound increased overall stability as the total energy of the compound is reduced compared to its constituent parts.

How much energy is there in a strong, medium and weak bond? Give examples of each type of bond (strong, medium and weak)

Examples of strong bonding are intermolecular bonds such as ionic and covalent bonds which can range in energy from a medium strength 150kJmol^-1 I-I bond to strong 950kJmol^-1 in a N≡N bond. The strength of bonds in this situation depends on the extent to which the valence molecular orbitals overlap and interact. Intermolecular bonding gives rise to much weaker forms of bond such as Van der Waals bonds and hydrogen bonding. These bonds arise from attractions between molecules or atoms that are otherwise not associated with one another. Hydrogen bonding as an example has energy of only around 5-30kJmol-1.

In some structures gaussview does not draw in the bonds where we expect, why does this NOT mean there is no bond?

Gaussview only draws in bonds when the atoms are less than a certain distance apart, this is pre-determined in the program and so the absence of a bond between two atoms only means that they are further apart than the distance set by the program. This does not mean that a bond does not exist as the distance is not indicative of whether there are the attractive forces and consequent stabilisation that define a bond.

Frequency Calculations

A frequency analysis is another form of calculation that can be performed using the gaussian software. This gives conformation that a minimum has been found and is the action of calculating the derivative of the optimisation or second derivative of the potential energy surface to confirm that the stationary point found in the optimisation is in fact a minimum value. For a minimum to be confirmed, the 'low frequencies' found in the log file should be as close to zero as possible, sitting within a range of ±15cm^-1. As well as confirming that a minimum has been found, a frequency analysis gives the vibrational modes of the molecule, allowing a spectrum to be produced based on the calculated molecule.

BH₃:B3LYP/6-31G(d,p)

Frequency file can be found here

Summary Data	Low Modes
	Low frequencies --- -14.1279 -14.1235 -10.2897 0.0010 0.0178 0.3550 Low frequencies --- 1162.9544 1213.1254 1213.1257

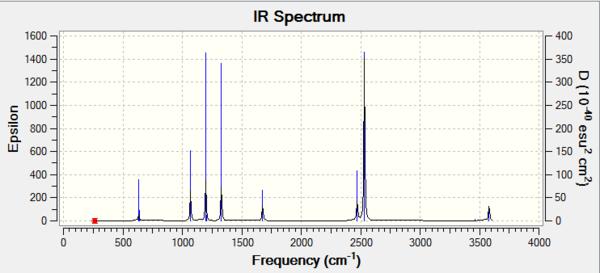
Vibrational spectrum for BH₃

wavenumber	Intensity	IR active?	type
1162	93	Yes	Bend
1213	14	Slight	Bend
1212	14	Slight	Bend
2582	0	No	Stretch
2715	126	Yes	Stretch
2715	126	Yes	Stretch

|

As can be seen, not all vibrational modes found actually show up in the spectrum generated. For a vibration to appear on the spectrum, i.e be IR active, it needs to induce a change in the dipole moment of the molecule. Examining the vibration animations for the six vibrations found show that all peaks are IR active to differing extents except for the peak at 2582cm^-1 which is not IR active and thus not seen in the spectrum.

GaBr₃:B3LYP/LANL2DZ

Frequency file can be found here

Summary Data	Low Modes
	Low frequencies --- -1.4877 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

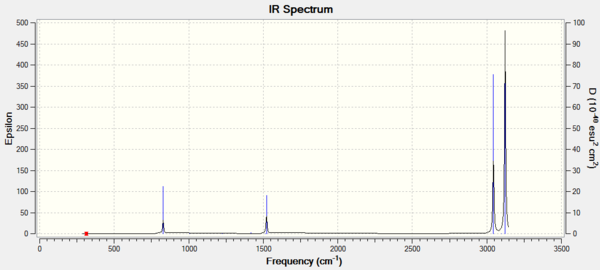
Vibrational spectrum for GaBr₃

wavenumber	Intensity	IR active?	type
76	3	Slight	Bend
76	3	Slight	Bend
99	9	Slight	Bend
197	0	No	Stretch
316	57	Yes	Stretch
316	57	Yes	Stretch

|

Vibrational Frequency Comparison

There is a very significant change in the frequency of the vibrations between BH₃ and GaBr₃, as can be seen in the tabulated values above, with the vibrations for BH₃ found at an order of magnitude higher than GaBr₃. In the equation that gives the frequency of the vibrations:

v=1/2π(k/μ)^½

There is a dependency on the reduced mass of the system and the force constant for the bond in question. The reduced mass simplifies a two body problems into a one body problem by combining the masses of both atoms into one mass term. This can be understood as the effective mass under force in the system. As BH₃ is a set of much lighter atoms than GaBr₃ it can be easily seen that BH₃ will have a much smaller reduced mass than GaBr₃ leading to a larger vibrational frequency. The force constant is characteristic of the bond in question and is greater where the bond is stronger and so keeping the system more rigid. As can be deduced from the bond length, the BH bonds are shorter and thus more rigid than Ga-Br bonds, so the BH bond, and vibrational frequency will be greater still. Both these factors give BH₃ much larger vibrational frequencies than GaBr₃.

BH3	GaBr3

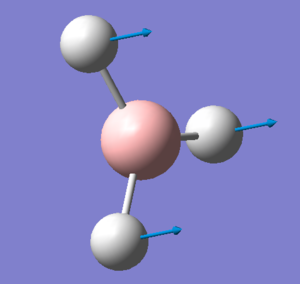
The above stills show the displacement vectors for the A2" umbrella motion in both BH₃ and GaBr₃. The vibrational frequency modes have reordered between the two molecules, with this motion of particular interest. In BH₃ this lies at 1162cm^-1 with an intensity of 93, whereas in GaBr₃ it lies at the much lower frequency of 99cm^-1 and an intensity of just 9. The reasons for the disparities in frequency have already been discussed above and can be applied again here. We expect the lighter atoms to move in the umbrella motion, which for BH₃ is obviously the hydrogen atoms, but in GaBr₃ the collective mass of the bromine atoms is more than the central gallium atom and so it is the gallium that moves rather than the bromines in GaBr₃.

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?

Performing the frequency analysis is running a calculation to find the derivative of the optimisation calculation. If a different method and basis set are chosen for the frequency calculation then the results have no real value as they have not used the same approximations as the geometry calculations.

What is the purpose of carrying out a frequency analysis?

As stated above, the frequency analysis gives the derivative of the optimised structure. This is also the same as the second derivative of the potential energy surface of the molecule and allows us determine the nature of the stationary points of the potential energy surface, if only positive values are found this confirms that the point in question is a minimum in the molecule. As has been done above, the IR spectrum of the molecule can also be predicted by conducting the frequency analysis of the molecule.

What do the "Low frequencies" represent?

Each linear molecule has 3N-6 vibrational modes. The low frequencies represent these “-6” modes and are translational and rotational modes of the centre of mass of the molecule.

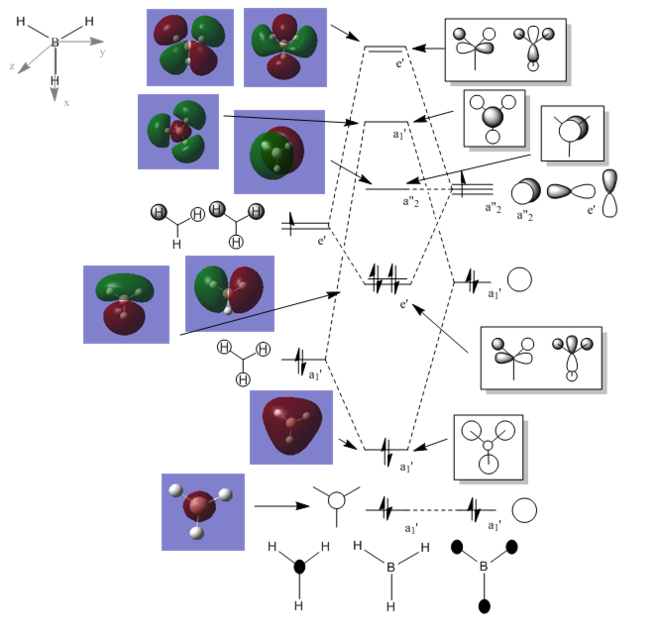
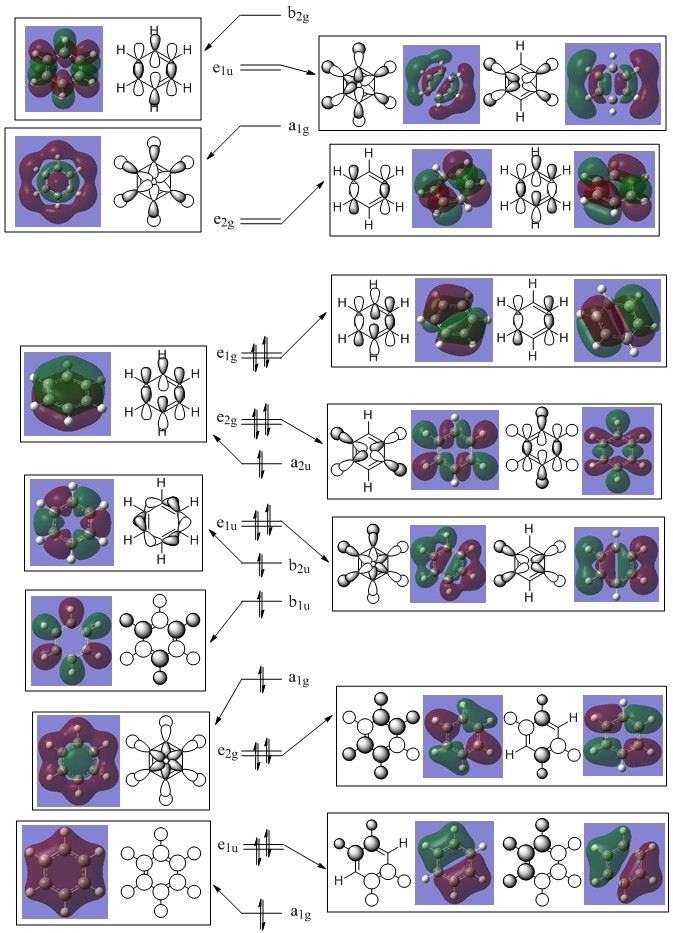
BH3 MO Diagram

Population file: DOI:10042/146829

This is the molecular orbital diagram for the BH₃ molecule, the black and white orbital drawing are the orbital shapes that are predicted by LCAO theory whereas the colour models on the left side of the diagram are the Gaussian calculated molecular orbitals. It can be seen that the LCAO predicted orbitals are a good approximation compared to the calculated MO’s however, they do not give a true idea of the size and spread of the orbitals over the molecule. When the simplicity of the LCAO method is considered, the method gives a very good approximation to the calculated values despite using very simple approximations.

NH3

The NH₃ molecule is optimised and a frequency analysis perfomed upon it. Another addition calculation, the population analysis is then performed upon it, allowing us to look at the distribution of charges in the molecule.

NH₃:B3LYP/6-31G(d,p)

Optimisation Log File: DOI:10042/146877

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000008 0.000040 YES Predicted change in Energy=-9.845953D-11 Optimization completed. -- Stationary point found.	Optimised BH3 Molecule

Frequency log file: DOI:10042/146892

Summary Data	Low Modes
	Low frequencies --- -0.0129 -0.0022 0.0017 7.0722 8.1014 8.1017 Low frequencies --- 1089.3849 1693.9369 1693.9369

Wavenumber	Intensity	IR active?	Type
1089	145	Yes	Bend
1694	13	Slight	Bend
1694	13	Slight	Bend
3461	1	Very Slight	Stretch
3590	0	No	Stretch
3590	0	No	Stretch

Population log file: DOI:10042/146925

Summary Data

NBO Analysis of NH₃

Charge range in the NBO Analysis shown below is -1 to +1.

Summary Data	Charge Data

The NBO pictures above allow an exploration of the charge distribution of the molecule. Each atom is visualised as a completely separate unit and the charge upon it given as a number.Above, the nitrogen atom is given a charge value of -1.125 and the hydrogen atoms all have a charge value of 0.375. As expected when considering the electronegativities of hydrogen and nitrogen, the highly electronegative nitrogen is seen to hold a large negative charge compared with the positive charges on the much more electropositive hydrogen.

Assosication Energies: Ammonia Borane

Ammonia and borane can be combined to form one NH3BH3 molecule with a dative covalent bond formed from the nitrogen to the boron. To calculate the association energy of forming the dative bond in ammonia-borane the following calculation can be performed, providing that the calcuations have been performed using exactly the same basis set and method (otherwise the results are meaningless.). As calculations using the B3LYP/6-31G(d,p) basis set and method have already been performed for the NH3 and BH3 molecules, performing the same calculations on the NH3BH3 molecule will allow the following equation to be used:

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]

NH₃BH₃:B3LYP/6-31G(d,p)

Optimisation Log File: DOI:10042/146971

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000034 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-1.180876D-10 Optimization completed. -- Stationary point found.	Optimised NH3BH3 Molecule

Frequency log file: DOI:10042/146977

Summary Data	Low Modes
	Low frequencies --- -2.6250 -0.0010 -0.0008 -0.0006 2.0137 3.7527 Low frequencies --- 263.4776 632.9557 638.4480

Wavenumber	Intensity	IR active?	Type
263	0	No	Bend
633	14	Slight	Stretch
638	4	Slight	Bend
638	4	Slight	Bend
1069	40	Yes	Bend
1069	40	Yes	Bend
1196	108	Yes	Bend
1204	3	Slight	Bend
1204	3	Slight	Bend
1329	113	Yes	Bend
1676	28	Yes	Bend
1676	28	Yes	Bend
2472	67	Yes	Stretch
2532	231	Yes	Stretch
2532	231	Yes	Stretch
3464	3	Slight	Stretch
3581	28	Yes	Stretch
3581	28	Yes	Stretch

All three energies have now be calculated and have been found to be (In AU):

E(NH3)= -56.5576873 a.u. E(BH3)= -26.6153236 a.u. E(NH3BH3)= -83.2246891 a.u.

This gives a total energy difference of -0.0516782 a.u. which when converted into kJmol^-1 gives us a association energy of 135.5kJmol^-1. When compared to the strength of bonds discussed before, this would be a weak bond. It has an energy much larger than the scale of weak, intramolecular bonding but is fairly weak when compared to other intermolecular bonds.

Extension: Manipulating charge distribution

Despite being isoelectronic, the central bond in ethane and ammonia borane is very different, one being a non-polar covalent bond, the other a dative covalent bond. By changing the charge distributions on the bonding atoms, we can manipulate the strength of the bond.

Ethane: B3LYP/6-31G level

Optimisation Log File: DOI:10042/161036

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000007 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-6.800923D-11 Optimization completed. -- Stationary point found.	Optimised Ethane Molecule

Frequency log file: DOI:10042/161039

Summary Data	Low Modes
	Low frequencies --- -1.8545 -1.8503 -0.0012 -0.0010 -0.0004 6.4037 Low frequencies --- 313.0588 828.0017 828.0018

NBO Analysis

Population Log files Ethane: DOI:10042/161043 Ammonia Borane: DOI:10042/161042

Ethane	Ammonia Borane

To compare the charge differences between the isoelectronic ammonia borane and ethane an NBO analysis has been conducted on both molecules.

Ethane	Ammonia Borane

A colour range of -0.500 to +0.500 was used for both diagrams.

Molecule	R1	R2	H1	H2	H3	H4	H5	H6
Ethane	-0.687	-0.687	0.229	0.229	0.229	0.229	0.229	0.229
Ammonia-Borane	-0.962	-0.171	0.436	0.436	0.436	-0.059	-0.059	-0.059

As can be seen from the charges on the molecules, the ethane has perfectly symmetric charges and so the bond can be expected to be a completely non-polar covalent bond. However, in ammonia-borane, there is a large charge difference, with the highly charged nitrogen supplying the electron density to the dative bond between them as the almost neutral boron lacks the electron density to contribute.

To see the effects of chemically manipulating the charges, a NBO analysis of NF3BH3 was performed.

NF₃BH₃: B3LYP/6-31G level

Optimisation Log File: DOI:10042/161258

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000010 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-1.079055D-10 Optimization completed. -- Stationary point found.	Optimised NF3BH3 Molecule

Frequency log file: DOI:10042/161270

Summary Data	Low Modes
	Low frequencies --- -4.4748 0.0008 0.0010 0.0017 3.4815 8.4014 Low frequencies --- 240.5102 303.1002 303.1529

NBO Analysis

Population Log file: DOI:10042/161043

A colour range of -0.500 to +0.500 was used.

R1	R2	H1	H2	H3	H4	H5	H6
0.717	-0.202	-0.165	-0.165	-0.165	-0.007	-0.007	-0.007

The table shows the charge distribution on the NBO analysis displayed above. By using the most electronegative atom possible, flourine, electron density has been pulled completely away from the nitrogen leaving it at a value of 0.717. Now, it is the boron that holds the negative, though only slight. If the B-N bond is considered now, the dative bond model from nitrogen used for NH3BH3 no longer seems reasonable as nitrogen holds a positive charge. A polar covalent bond must now exists, and having removed electron density from the bonding atoms overall, the bond will have been significantly weakened.

The ability to use computational modeling to alter bonds in this fashion is very useful, allowing predictions about the proposed effects of altering molecules to be tested in this way before synthesis is attempted, reducing the time and cost that could be incurred by unnecessary synthesis.

Aromaticity

Introduction to Project

In this mini project, the topic under investigation will be aromaticity. After learning the techniques needed to perform this investigation in the first half of the lab, focus now moves to comparing four aromatic systems; benzene, boratabenzene, pyridinium, and borazine. Comparisons will be made by performing an optimisation, frequency analysis and population analysis to calculate the molecular orbitals for each moleculr, using benzene as a reference standard with which to compare the other three.

Benzene

As benzene is the reference molecule in this project, a full MO diagram has been drawn from the calculated MO's, this allows a discussion of what aromaticity actually means in reference to these MOs. As with all the molecules in this project an optimsation, frequency analysis, and population analysis have been performed on the benzene molecule.

B3LYP/6-31G(d,p) level

Optimisation Log File: DOI:10042/149868

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000002 0.000060 YES RMS Displacement 0.000001 0.000040 YES Predicted change in Energy=-6.700829D-12 Optimization completed. -- Stationary point found.	Optimised BH3 Molecule

Frequency log file: DOI:10042/149865

Summary Data	Low Modes
	Low frequencies --- -10.2549 -5.6651 -5.6651 -0.0056 -0.0056 -0.0009 Low frequencies --- 414.5451 414.5451 621.0429

Wavenumber	Intensity	IR active?	Type
415	0	No	Bend
415	0	No	Bend
621	0	No	Bend
621	0	No	Bend
695	74	Yes	Bend
718	0	No	Bend
865	0	No	Bend
865	0	No	Bend
975	0	No	Bend
975	0	No	Bend
1013	0	No	Bend
1018	0	No	Bend
1020	0	No	Stretch
1066	3	Very Slight	Bend
1066	3	Very Slight	Bend
1180	0	No	Bend
1203	0	No	Bend
1203	0	No	Bend
1355	0	No	Stretch
1381	0	No	Bend
1524	7	Slight	Stretch
1524	7	Slight	Stretch
1653	0	No	Stretch
1653	0	No	Stretch
3172	0	No	Stretch
3181	0	No	Stretch
3181	0	No	Stretch
3197	47	Yes	Stretch
3197	47	Yes	Stretch
3208	0	No	Stretch

Population Analysis

Charge Distribution

The charge distribution shown here is from -0.239 to +0.239

Summary Data	Charge Data

Benzene MO Diagram

For a molecule to be considered aromatic, it must fulfill certain criteria:

- The molecule must posses a delocalised π system of electrons

- It must have a planar structure with respect to the involved atoms

- The atoms involved must be a ring structure

- Huckel's Rule must be satisfied: It states that the system must have 4n + 2 π electrons to be considered aromatic

We can see from our optimised molecule that benzene satisfies the second and third criteria, and the electron count does qualify benzene as aromatic. The energy level diagram for benzene below complete with the calculated MO's shows us the delocalised π system of electrons, the a2u symmetry orbital. As benzene fulfills all the criteria for aromaticity, the calculations have confirmed what was already known about the aromaticity of benzene.

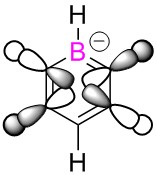
Boratabenzene

Boratabenzene is a molecule, isoelectronic with benzene, that has a B-H unit in place of a C-H unit and carries an overall negative charge. Below, it has been optimised, and a frequency analysis and population analysis performed on it's optimised form.

Optimisation

Optimisation Log File: DOI:10042/152813

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000007 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000032 0.000060 YES RMS Displacement 0.000009 0.000040 YES Predicted change in Energy=-4.417167D-10 Optimization completed. -- Stationary point found.	Optimised Boratabenzene Molecule

Frequency Analysis

Frequency log file: DOI:10042/152878

Summary Data	Low Modes
	Low frequencies --- -7.2579 0.0003 0.0006 0.0006 3.1967 4.5275 Low frequencies --- 371.2965 404.4162 565.0822

Population Analysis

Population log file: DOI:10042/152913

NBO Analysis

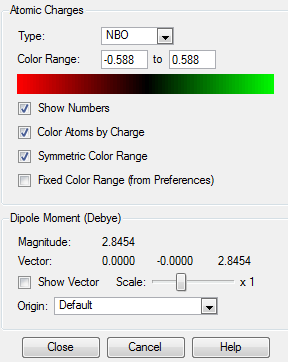
A charge range of between -0.588 and 0.588 is shown in the coloured charge range below.

Atom	Charge
Boron	0.202
Hydrogen 2 & 6	0.184
Carbon 2 & 6	-0.588
Hydrogen 3 & 5	0.179
Carbon 3 & 5	-0.250
Hydrogen 4	0.185
Carbon 4	-0.340
Hydrogen 1	-0.096

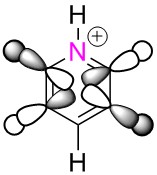
Pyridinium

Pyridinium is a molecule, isoelectronic with benzene, that has an N-H unit in place of a C-H unit and carries an overall positive charge. Below, it has been optimised, and a frequency analysis and population analysis performed on it's optimised form.

Optimisation

Optimisation Log File: DOI:10042/153075

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000007 0.000060 YES RMS Displacement 0.000002 0.000040 YES Predicted change in Energy=-7.254442D-11 Optimization completed. -- Stationary point found.	Optimised Pyridinium Molecule

Frequency Analysis

Frequency log file: DOI:10042/153111

Summary Data	Low Modes
	Low frequencies --- -9.3844 -2.9848 0.0003 0.0005 0.0008 0.9989 Low frequencies --- 391.9005 404.3428 620.1998

Population Analysis

Population log file: DOI:10042/153129

NBO Analysis

A charge range of between -0.483 and 0.483 was used for the below charge distributions.

Atom	Charge
Nitrogen	-0.476
Hydrogen 2 & 6	0.285
Carbon 2 & 6	0.071
Hydrogen 3 & 5	0.297
Carbon 3 & 5	-0.241
Hydrogen 4	0.292
Carbon 4	-0.122
Hydrogen 1	0.483

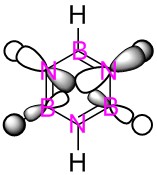
Borazine

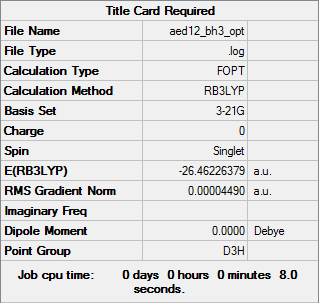
Borazine, often referred to as 'inorganic benzene', is comprised of alternating B and N atoms in a six membered ring, it is also isoelectronic with benzene and has no overall charge. Below, it has been optimised, and a frequency analysis and population analysis performed on it's optimised form.

Optimisation

Optimisation Log File: DOI:10042/153222

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000010 0.000015 YES RMS Force 0.000005 0.000010 YES Maximum Displacement 0.000056 0.000060 YES RMS Displacement 0.000018 0.000040 YES Predicted change in Energy=-3.023822D-09 Optimization completed. -- Stationary point found.	Optimised Borazine Molecule

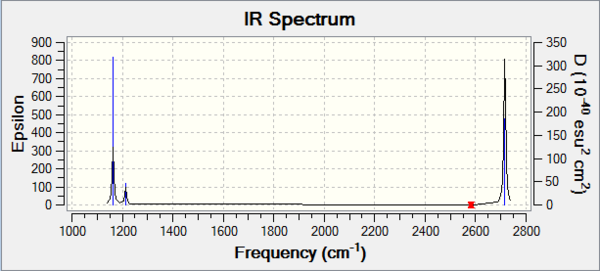
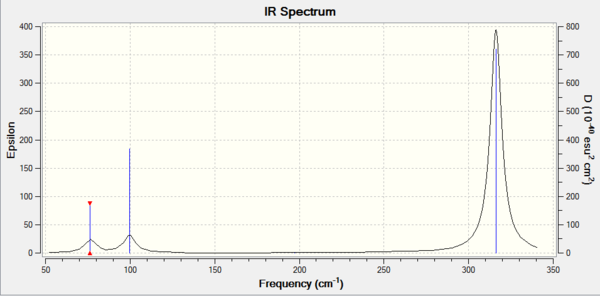
Frequency Analysis

Frequency log file: DOI:10042/153237

Summary Data	Low Modes
	Low frequencies --- -4.4958 -4.4782 -3.4787 -0.0038 0.0137 0.0184 Low frequencies --- 289.7312 289.7319 404.5218

Population Analysis

Population log file: DOI:10042/153267

NBO Analysis

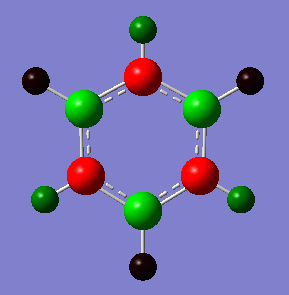
A charge range of between -1.102 and +1.102 was used for this NBO analysis

Atom	Charge
Boron	0.747
Nitrogen	-1.102
Boron Attached Hydrogen	-0.077
Nitrogen Attached Hydrogen	0.432

Molecule Comparison

Computing all four molecules in the exact same way using the same method and basis set provides a set of data for each molecule that can be directly compared across the series to allow conclusions about the effects of the differences in the molecules to be drawn. Comparisons between various properties of the molecules have been made, from bond angles to direct comparison of some of the MO's.

NBO Comparison

Benzene	Boratabenzene	Pyridinium	Borazine

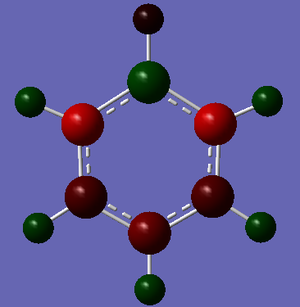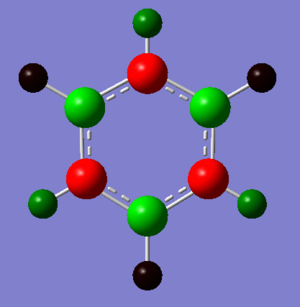
Molecule	A1	A2	A3	A4	A5	A6	H1	H2	H3	H4	H5	H6
Benzene	-0.239	-0.239	-0.239	-0.239	-0.239	-0.239	0.239	0.239	0.239	0.239	0.239	0.239
Boratabenzene	0.202	-0.588	-0.250	-0.340	-0.250	-0.588	-0.096	0.184	0.179	0.186	0.176	0.184
Pyridnium	-0.476	0.071	-0.241	-0.122	-0.241	0.071	0.483	0.285	0.297	0.292	0.297	0.285
Borazine	-1.102	0.747	-1.102	0.747	-1.102	0.747	0.432	-0.077	0.432	-0.077	0.432	-0.077

The charge distributions shown above have a fixed colour range from -1.000 to 1.000 to allow direct comparison of the charges between diagrams. The differences in charge distribution arise as a direct consequence of the electronegativities of the atoms in the molecules, which are tabulated below. Electronegativity is a measure of the ability of an atom to attract electrons in a bond toward itself and is dependent on both the nuclear charge of the molecule and the extent to which it's electrons experience shielding.

Atom	Electronegativity (Pauling)
Hydrogen	2.20
Carbon	2.55
Boron	2.04
Nitrogen	3.04

Firstly, Benzene. The very high symmetry of the molecule (Point Group D_6h) gives a perfectly symmetrical charge distribution with respect to all the carbons and hydrogens, and the higher electronegativity of the carbon atoms means they hold a greater proportion of the electron density of the molecule. This can be seen from the pictures above, the red colour representing a negative charge and the green a positive charge. The brighter these colours are, the higher the relative charge.

In Boratabenzene, on of the C-H units has been replaced with a B-H unit and the molecule also carries an overall charge of -1. As Boron is less electronegative than carbon and hydrogen, we now see that the hydrogen attached to the boron atom (H1) carries a higher proportion of electron density than the boron, as the electronegativity difference is smaller than that between Carbon and Hydrogen (0.16 vs 0.35) the charge distribution is less extreme than in benzene, with the hydrogen only holding a very slight negative charge. However, there is also another factor affecting charge distribution between B and H atoms, the Boron is also bonded to two carbon atoms. As the carbon and boron do not have identical electronegativities, the bond between them is polar covalent and there is an unequal distribution of charge density between them. The carbon is more electronegative and thus holds a greater proportion of the charge between them. The presence of the boron atom in the ring has an effect on the whole π system of the ring, as boron itself is electronegative it holds a smaller amount of electron density than it's equivalent carbon atom in benzene. This extra electron charge is shared between the remaining five carbon atoms with the carbons bonded to the boron and the carbon in position four having a greater electron density than in benzene. The carbon bonded hydrogens show electron densities ranging from almost exactly as those in benzene to slightly lower due to the increased charge on the carbon. When the charge is increased on the carbon due to the presence of the boron, it has no effect on the extent to which charge is shared between the carbon and hydrogen as the electronegativity difference between them has not changed. The values however do change as there is a different level of charge in the C-H unit as a whole that needs to be distributed.

Pyridine is similar to boratabenzene in that one C-H unit has been replaced, however, in this case it has been replaced by a N-H unit, and as nitrogen is more electronegative than carbon and hydrogen it has the opposite effect to the presence of the boron atom. As the electronegativity difference is greater between nitrogen and carbon than for boron and carbon (0.49 vs 0.41) the effects are slightly more pronounced than in boratabenzene. In this case we see a more electron deficient hydrogen attached to the nitrogen compared to benzene and the remaining five carbons in the ring have a lower proportion of electron density on them due to the more electronegative nitrogen drawing a greater amount of charge from the π system onto itself versus the carbons. The charges of the carbons show the same patterns as those in boratabenzene with the carbons ortho and para to the nitrogen atom of a higher charge than those in the meta position.

Borazine, an inorganic analogue of benzene with three B=N units joined to make a six membered alternating boron and nitrogen ring. As boron and nitrogen have a large electronegativity difference (1.00) compared with either boron and carbon (0.41) or nitrogen and carbon (0.49) the difference in charge distribution in borazine is much more stark than in boratabenzene or pyridinium. As expected, the more electronegative nitrogen holds a much greater charge than the boron atoms and as a result the hydrogens attached to the borons carry a slight negative charge versus the positively charged nitrogen attached hydrogens.

Bond Comparison

The effects of electronegativity and the resulting charge distributions can also be illustrated through the changes in bond angles and lengths. As discussed in the first half of the lab, bond strengths and sizes are intimately linked. We can see from the ring bond angles that the smaller, electropositive boron can create a smaller ring angle. This is due to it's smaller size, and the converse effect is seen with the larger nitrogen atom.

Bond Angles / Degrees (°)

Benzene C-C-C	Boratabenzene C-B-C	Pyridinium C-N-C	Borazine B-N-B	Borazine N-B-N
120.0	115.1	123.3	117.1	122.9

When bond lengths are examined, it's helpful to make comparisons to the charge distributions. In boratabenzene, B-C bonds are longer than C-C bonds in benzene, due to the reduced electronegativity of boron less able to polarise carbon to create the bond and also due to poorer orbital energy match up. C-H bond are also significantly longer, due to the greater amount of charge between the hydrogen and carbon in boratabenzene. C-C bond lengths are similar, this makes sense due to the charge distributions on the carbons not being too dissimilar to benzene.

In pyridinium, the opposite effects are observed, with the C-N bond length shorter than the benzene C-C due to nitrogen's greater electronegativty and thus stronger pull on the electrons in the bond, shortening the bond. The C-H bonds and C-C bonds are also of a comparible or slightly shorter length due to the opposite effect as in boratabenzene.

Borazine shows longer N-H bonds than pyridinium and shorter B-H bonds than in boratabenzene.

Benzene

	C-C	C-H
r(E-X) (Å)	1.40	1.09

Boratabenzene

	B-C	B-H	C-H	C-C (C2-C3)	C-C (C3-C4)
r(E-X) (Å)	1.51	1.22	1.10	1.40	1.41

Pyridinium

	N-C	N-H	C-H	C-C (C2-C3)	C-C (C3-C4)
r(E-X) (Å)	1.35	1.02	1.08	1.38	1.40

Borazine

	B-N	B-H	N-H
r(E-X) (Å)	1.43	1.00	1.20

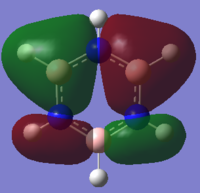
MO Comparison

	Benzene	Boratabenzene	Pyridinium	Borazine
MO
LCAO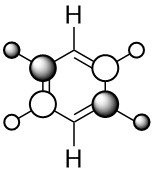
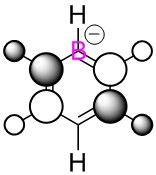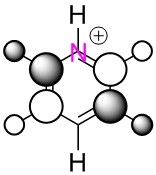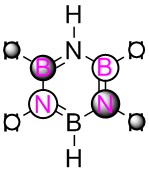
Ordering	11	10	11	12
Energy (a.u.)	-0.59736	-0.36649	-0.85982	-0.52456
Degenerate?	Yes	No	No	Yes

The first compared MO shows a MO created through medium through bond orbital interaction between in phase s orbitals on both the carbon in ring positions 2,3,4, and 5 and their attached hydrogen's s orbitals. In addition to this there are also weak through space anti bonding interactions between s orbitals on neighbouring carbons and very weak through space anti bonding interactions between s orbitals on neighbouring hydrogens. In this case, benzene shows four symmetric areas of electron density of alternate phase going around the ring.

We can clearly see the influence of substitution of atoms from the MO's of boratabenzene, pyridinium and borazine. Where we have the more electronegative nitrogen atoms, we see the MO's distorted to attempt to cover the nitrogen atoms more, and conversely with the more electropositive boron, a tendency to pull away from it in favour of the more electronegative carbons/nitrogen.

The substitution of the C-H unit for a B-H or N-H unit reduces the symmetry and breaks the high level of degeneracy that we see in benzene, and to a lesser extent in borazine. Therefore we see that only for benzene and borazine is this orbital degenerate. The differences in order are linked to the energy of the orbitals, the electronegative nitrogen is well able to stabilise the electron density it draws and thus we see that the pyridinium orbitals is significantly lower in energy than the benzene orbital. The opposite, a destablisation, occurs in the case of boratabenzene whose electropositive boron is less able to stablise the charge than a carbon would, thus showing a higher energy MO.

Borazine shows a combination of these stabilising and destablising effects, and the corresponding poorer orbital size match between boron and nitrogen versus just carbons can help to explain the overall destabilisation of the borazine MO compared to benzene.

The LCAO's for these orbitals manage to predict the overall shape of the MO's fairly well, but as with all the compared MO's their downfall is showing how the orbitals extend over the full molecule, and the aforementioned effects of the electronegativity on the orbital shape.

	Benzene	Boratabenzene	Pyridinium	Borazine
MO
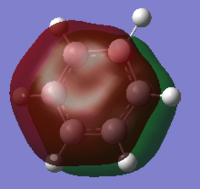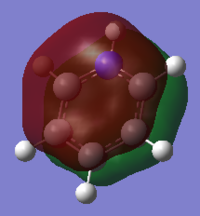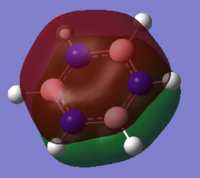
LCAO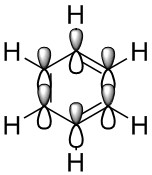
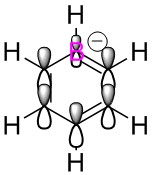Ordering	17	17	17	17
Energy (a.u.)	-0.35994	-0.13210	-0.64062	-0.36133
Degenerate?	No	No	No	No

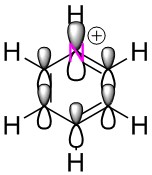
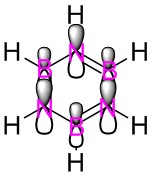
This MO is the characteristic aromatic delocalised π electron system. It is comprised of P orbitals that lie on each atom perpendicular to the plane of the ring itself, these orbitals show only strong through space bonding interactions to create a delocalised cloud of electron density above and below the ring.

When comparing the MOs across the molecules, there are only subtle differences in shape, with all forming the characteristic cloud above and below the ring. Where there is substitution of a C-H unit in boratabenzene and pyridinium the cloud is distorted, away from the electropositive boron and toward the electronegative nitrogen. In borazine, we see a balance of these two effects, with the MO extending more over nitrogen and away from boron.

With respect to the ordering, all lie in 17th position, and all display no degeneracy, this reflects the fact that the MO is a key component of the aromaticity of each molecule. We see the same trends in energy as in the first example with the exception of borazine, whose orbital is deeper in energy than the benzene MO. The two MO's are very close in energy and it is difficult to explain exactly why some of borazines MO's are higher in energy than benzene and some are lower as in these first two compared MO's, as we're always seeing a balance between the stability of charge from nitrogen and the destability from boron.

	Benzene	Boratabenzene	Pyridinium	Borazine
MO
LCAO
Ordering	18	19	18	18
Energy (a.u.)	-0.33960	-0.08375	-0.57739	-0.31992
Degenerate?	Yes	No	No	Yes

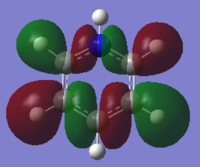
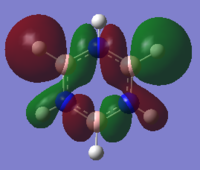
These MO's show in phase through bond interactions between the hydrogen s orbitals and p orbitals on the ring atoms, as well as through space out of phase anti bonding interactions between the p orbitals on the ring atoms. This added anti bonding character from the p orbitals puts this orbital higher in energy than the two previous orbitals compared, lying at position 18 for all but boratabenzene where it lies at position 19. As in the first example, we see a break in degeneracy for boratabenzene and pyridinium due to reduced symmetry so for only benzene and borazine is this MO part of a degenerate pair. For boratabenzene and pyridinium the degenerate set will be split to one higher energy, one lower energy at positions 18/19, hence why we see this orbital at position 19 for boratabenzene.

As for the energy of the molecule, we see the same trend as the first example, with boron and nitrogen destablisiing and stabilising the energy of the orbital respectivley. Borazine and Benzene again lie very close in energy due to their high symmetry and the balance of effects in borazine.

Comparison of MO Levels

It's clear to see from all the above comparisons that small changes to the structure of benzene have large effects on the chemical properties of the molecule. From the bond lengths to the MO energy levels, there have been changes in almost all properties due to changes in the electronegativites of atoms. Changing the electonegativities and electronic properties of the atoms involved show changes in the charge distribution around the molecule.

Examining the energy levels of the molecules can allow us to see exactly how the substitutions made affect the whole stability of the molecule. Every substitution made has broken the symmetry of the molecule, when exchanging a C-H unit the symmetry is reduced so far that we no longer see any degenerate sets of orbitals. In borazine, the symmetry is reduced but not to as great as extent as boratabenzene and pyridinium so it still shows some degeneracy. These breaks in symmetry are illustrated by looking at the point groups for each molecule.

Benzene	Boratabenzene	Pyridinium	Borazine
D6h	C3v	C3v	D3h

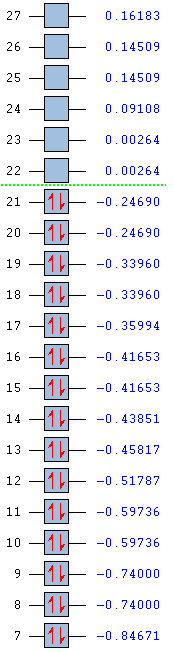
Boratabenzene is the least stable overall molecule. Looking at it's MO energy levels, all sit significantly higher than the corresponding energy levels in benzne. This is all a direct result of the more electropositive nature of boron, it's lower electronegativity means it is less able to stablise the electronic charge from the ring, raising the energy of its MOs. This also makes it the most reactive molecule of the four, with it's HOMO sitting at -0.03492, making it only a very slightly bonding orbital overall. It also has a filled orbital 21 which can be seen in MO diagram to be an antibonding orbital, a further source of destablisation.

Pyridinium, having had a C-H unit replaced with a N-H unit, also has it's overall energy changed significantly. However, in this case the more electronegative nitrogen is more able to stabilse the electronic charge, affording the whole molecule extra stability. Following in the same vein, it is also the least reactive molecule, with it's HOMO lying at a much stronger bonding -0.47886.

Borazine, with it's balance of destabilsing boron and stabilising nitrogen has energy levels that much more closely resemble those of benzene. But the corresponding orbitals between them are not always stabilised or destabilised, their energy levels fluctuate above and below those of benzene.

Benzene	Boratabenzene	Pyridinium	Borazine

Conclusion

Despite all molecules studied being aromatic, isoelectronic and of the same basic structure, this project has shown just how different the properties of the molecules can be, just by varying the electronegativities of the atoms involved. There have been shown to be large variations in symmetry, bond lengths and angles, stability and MOs. With respect to benzene, the project has seen variation from the largely destabilised boratabenzene, to the highly stabilsed pyridinium. The MO's of each molecule have also been studied, and the benzene MO diagram constructed in full to investigate the features that contribute to aromaticity.

Extension: Antiaromaticity

To expand the understanding of the origins of aromaticity and it's effects on the bonding and MO's of molecules, the situation of the opposite properties must be explored, antiaromaticty. As explined before, aromaticty arises from the satisfaction of certain conditions:

- The molecule must posses a delocalised π system of electrons

- It must have a planar structure with respect to the involved atoms

- The atoms involved must be a ring structure

- Huckel's Rule must be satisfied: It states that the system must have 4n + 2 π electrons to be considered aromatic

To be classed as antiaromatic, a molecule must have all the above critera filled excpet the last point, where it must have 4n π electrons rather than 4n + 2. A non aromatic molecule can also have either 4n or 4n + 2 π electrons but it will fail to satisfy one of the other three critera.

To study the differences between aromatic and antiaromatic molecules, an optimisation, frequency analysis and population analysis have been carried out on two similar molecules: the cyclopentadienyl anion and cation. The anion is aromatic and the cation is antiaromatic and their identical structures bar charge allow the best comparison of the effects of aromaticty and anti aromaticity on a molecule.

Cyclopentadienyl Cation: B3LYP/6-31G level

Optimisation Log File: DOI:10042/161062

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000016 0.000060 YES RMS Displacement 0.000005 0.000040 YES Predicted change in Energy=-3.999490D-11 Optimization completed. -- Stationary point found.	Optimised Cation

Frequency Analysis

Frequency log file: DOI:10042/161077

Summary Data	Low Modes
	Low frequencies --- -0.0003 0.0005 0.0010 3.3749 4.9200 6.3395 Low frequencies --- 267.6475 339.9515 490.6088

Population Analysis

Population log file: DOI:10042/161078

Cyclopentadienyl Anion: B3LYP/6-31G level

Optimisation Log File: DOI:10042/161075

Summary Data	Low Modes	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000001 0.000060 YES RMS Displacement 0.000000 0.000040 YES Predicted change in Energy=-1.638372D-12 Optimization completed. -- Stationary point found.	Optimised Anion

Frequency Analysis

Frequency log file: DOI:10042/161079

Summary Data	Low Modes
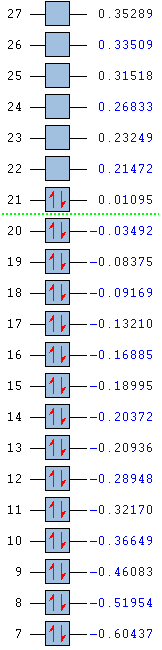
	Low frequencies --- -0.0019 -0.0019 -0.0009 5.1366 6.6788 6.6788 Low frequencies --- 600.7483 600.7483 620.6363

Population Analysis

Population log file: DOI:10042/161080

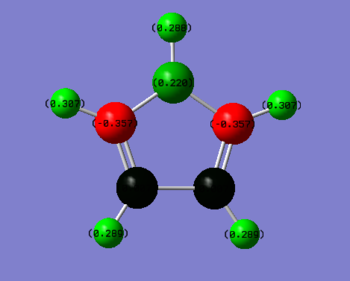
NBO Analysis

Cation	Anion

Molecule	A1	A2	A3	A4	A5	H1	H2	H3	H4	H5
Cation	0.220	-0.357	0.007	0.007	-0.357	0.288	0.307	0.289	0.289	0.307
Anion	-0.377	-0.377	-0.377	-0.377	-0.377	0.177	0.177	0.177	0.177	0.177

As expected, the fully symmetrical aromatic anion shows a fully symmetrical charge distribution with the more electronegative carbon atoms holding a negative charge and the more electropositive hydrogens holding a positive charge. The cation on the other hand, displays a very unusual charge distribution, the antiaromatic cation has a delocalised π electron cloud yet this only contains four electrons, rather than the six in the cloud of the anion. This means that there is less negative charge to be spread over the molecule, and the carbon in the top position, being bonded to two double bonding carbons which are pulling density away has a positive charge. This is a difference in charge density of 0.597 when compared with the carbons in the anion.

The carbons in positions 2 and 5 benefit from the added electron density that comes from the double bond but still lie slightly lower in charge than the anion carbons. The carbons in position 3 and 4 are bonded to another carbon that is part of a double bond, this reduces their share of electron density and results in two almost completely neutral carbons.

When hydrogens in the molecules are compared, all hydrogens in the cation are more positive than those in the anion, due to the reduced amount of electron density available in the system.

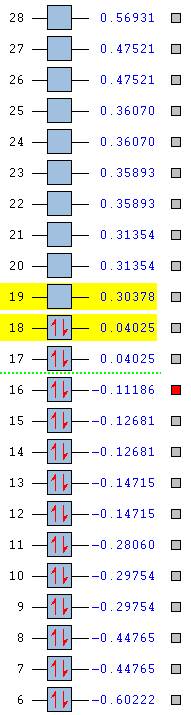
MO Comparison

Shown below are the MO energy levels of the cyclopentadienyl anion and cation. It is already known that the anion is aromatic and the cation is antiaromatic, however their MO diagrams display some curious behaviours. Despite being antiaromatic, a destablising quality, the cation's corresponding energy levels are deeper than those of the aromatic anion. It has a much lower energy LUMO and HOMO and all it's filled orbitals are bonding, unlike the anion which has filled antibonding orbitals. However, when the overall energies of the molecules are examined, it is found the despite having 36 electrons versus the cation's 34 the anion only lies a small amount higher in energy. This added extra pair of electrons would usually be expected to add a much larger energy contribution than is actually seen, reinforcing the idea that the anion gains added stability from it's aromaticity.

Cation	Anion

The two MO's shown below are the delocalised π systems of electrons for both the anion and the cation. As the delocalised system is a requirement for both antiaromatic and aromatic molecules, the MO's shown prove, along with the electron count that the cation and anion both satisfy the antiaromatic and aromatic criteria respectively. Interestingly, there is no change in shape between the two MO's despite the large differences in the molecule. Where we do see a difference is in the energy of each MO. For the anion, this MO is number 17 and has an energy of 0.04025 whereas the cation's MO is number 15 and has an energy of -0.60210.

Cation	Anion