Rep:Mod:adb128

Cope Rearrangement

In this exercise we will be studying transition states in molecules large enough that regular molecular mechanics and simple calculations will not work. We will locate transition structures using molecular orbital-based methods and numerically solve the Schrodinger equation. This study of potential energy surfaces allows us to also look at transition structures, reaction paths and barrier heights. Several different transition states will be studied here, firstly the [3,3] Cope Rearrangement, focusing on the boat and chair transition structures, and then we will focus on the transition structures involved in Diels-Alder reactions.

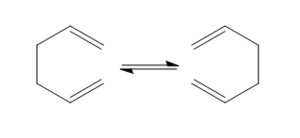
The [3,3] Cope Rearrangement has been the subject of much discussion relating to the transition state of the reaction. It is now widely agreed that it occurs in a concerted fashion via a 'chair' or 'boat' transition structure. In the following exercise we will study the low energy minima and transition structures of 1,5-hexadiene and subsequently determine the preferred mechanism. The rearrangement is depicted below:

The 1,5-hexadiene molecule three carbon-carbon bonds which are able to readily rotate. This means that there are 27 possible conformations of the 1,5-hexadiene molecule but only 10 of these are energetically distinct due to symmetry etc. These have been simulated using the GaussView program. The conformers have a variety of Gauche- and Anti- linkages across the central four atoms and were all optimised using the Hartree Fock method in Gaussian with the 3-21G basis set. Shown below are the structures, point groups and energy of the molecules that were studiedː

Nf710 (talk) 16:46, 1 December 2015 (UTC) Nice intro, you clearly understand the chemistry that is going on here. but more understanding of the methods used here would have been nice.

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy/kcal/mol
anti1		C2	-231.692602	0.04
anti2		Ci	-231.692535	0.08
anti3		C2h	-231.689071	0.08
anti4		C1	-231.690971	1.06
gauche		C2	-231.687716	3.10
gauche2		C2	-231.691667	0.62
gauche3		C1	-231.692661	0.00
gauche4		C2	-231.691530	0.71
gauche5		C1	-231.689616	1.91
gauche6		C1	-231.689160	2.20

From the above optimizations we can see that the confirmation with the lowest energy is the Gauche 3 conformer. This stability can likely be attributed to the positive interaction between the C=Cπ orbital and the vinyl proton. The sterics of the molecule contribute to the high energy of the highest energy confirmation (Gauche1) where the vinyl groups are too close and so electronically disfavoured. In fact, the difference in energy between the confirmations can largely be explained by the distance between the vinyl groups. The difference in energy for the anti conformers can be attributed to the repulsion between the protons on the β carbon and the vinyl protons, and thus energy is related to the distance between these protons with shorter distances leading to less stable conformers.

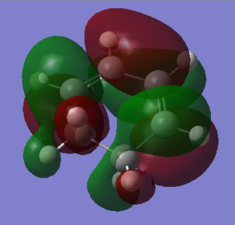
This difference in energy between the most stable and least stable conformers can easily be seen in the orbital overlap, as shown belowː

Gauche1	Gauche3

Nf710 (talk) 16:53, 1 December 2015 (UTC) Very nice, using the orbitals to compare the energies for the highest and lowest conformer, you have clearly gone beyond the script here. well done.

Comparison of Theories (HF/3-21G and B3LYP/6-31G*)

We now re-optimize our Anti2 conformation of 1,5-hexadiene using the B3LYP/6-31G* method. The Hartree Fock method that we had previously used was based on using one-electron spin-orbitals to iteratively solve the Schrodinger equation via a mean electron repulsion term. The B3LYP method that we will now use uses Density Functional Theory to optimize electron density to approximate the potential felt by each electron. This method allows for consideration of the interactions between electrons and so is more powerful.\

Nf710 (talk) 16:56, 1 December 2015 (UTC) very nice brief explanatation of the theory

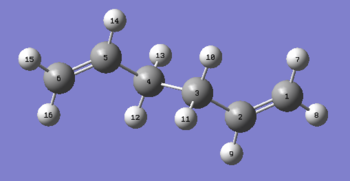
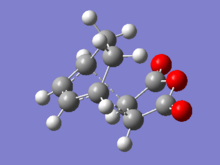
Whilst the two molecules appear very similar visually, on closer inspection there are small differences in their geometry. These are detailed in the table below, with reference to the numbering present in the numbered molecule below:

Optimization	Length C1-C2 (Å)	Length C2-C3 (Å)	Length C3-C4 (Å)	Angle C1-C2-C3 (°)	Angle C2-C3-C4 (°)
HF/3-21G	1.316	1.509	1.553	124.81	111.35
B3LYP/6-31G*	1.338	1.507	1.555	125.21	112.64

It can be seen that there are not huge differences in the geometries between the two levels of theory. The bond length for C1-C2 is significantly larger for the B3LYP/6-31G* level of theory, taking it to a value much closer to the literature value of 1.33Å. The fact that there are only small differences between the two computational methods shows that the Hartree Fock is a good approximation. This means that we can use the low computational cost of a simple approximation to produce a very good starting point to then refine with the more computationally demanding higher levels of theory.

Nf710 (talk) 16:59, 1 December 2015 (UTC) Good comparison of the geoms. and good understanding of how we use different levels of theory

Frequency Analysis

We will also perform a frequency analysis on the optimised structure calculated at the B3LYP/6-31G* level of theory. The frequency is related to the second derivative of the potential energy surface, taking in to account the geometries of the atoms involve. This means that the frequencies can give us further information relating to the stationary point of the potential energy surface.

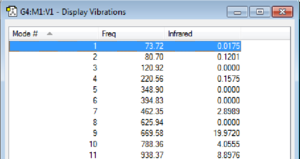
The frequencies should all be positive (and thus real) for this molecule under the B3LYP/6-31G* level of theory if the minimum has correctly been calculated. This is because the second derivative calculated is the force constant and in the harmonic oscillator equation this value is square rooted, thus any negative force constants would produce an imaginary frequency.

Nf710 (talk) 17:16, 1 December 2015 (UTC) Good understanding, however in future it would be good to have the equation in there.

Energies/Enthalpies Added	Total Energy/Enthalpy
Sum of electronic and zero-point Energies	-234.469214
Sum of electronic and thermal Energies	-234.461866
Sum of electronic and thermal Enthalpies	-234.460922
Sum of electronic and thermal Free Energies	-234.500800

The top of the table of frequencies showing none were negative is displayed belowː

Optimizing the 'Chair' and 'Boat' Transition Structures

Optimization of the Chair Transition Structure

Hartree Fock Method

The chair transition state is optimised first. This is done by first optimizing an allyl fragment (C₃H₅) which is then duplicated and the two fragments are then placed 2.2Å apart with a C_2h point group. We will use the Hartree Fock method with a 3-21G basis set but we will use the TS(Bermy) method as we are dealing with a transition state. The optimised transition structure is shown below.

The singular negative frequency is present at -817.88, confirming the presence of a minimum and thus a transition state.

Frozen Coordinate Method

This is an alternative method to optimise the chair transition state using the same level of theory (3-21G) with the Hartree Fock method. We will again set the distance between the fragments to 2.2Å but this time we will freeze the ends of the molecules to this distance throughout the course of the optimisation. The molecule is then optimised again with the bonds unfrozen.

The two structures are visually almost exactly the same geometry. On further analysis we can see that leaving the terminal carbons free actually marginally increases the distance from 2.200Å to 2.209Å and the frequency value also slightly increases, moving from -817.88 to -817.94. These differences are incredibly small which tells us that the frozen coordinate method will allow us to make a good approximation, but the Hartree Fock method without modifications takes us closer to the literature values and so can be considered the more reliable method.

Nf710 (talk) 17:09, 1 December 2015 (UTC) You should have referenced literature here if you are quoting it.

QTS2 Optimisation

We will now optimise the boat transition structure using the QTS2 Method. In this method we specify the starting reactants and end products to find the transition structure. In order for this method to work the products and reactants must be appropriately numbered so that they match one another to allow for the pathway between them to be found. An initial input of the Anti 2- 1,5-hexadiene molecule (as show below) fails to produce the boat transition structure as the simulation assumes that there will be a translation of the top allyl fragment instead of the central bond rotation that we are looking for.

To try and actually achieve the boat transition structure, we edit the angles of the reactant and product molecules to a more eclipsed conformation, as shown belowː

Because these structures are closer to the transition structure, we are able to visualise the boat transition structureː

Upon examination of the vibrational modes, we find a single negative vibration at 839.9cm^-1 which corresponds to the transition state vibration and thus confirms that we have found the maximum saddle point.

Intrinsic Reaction Coordinate Method

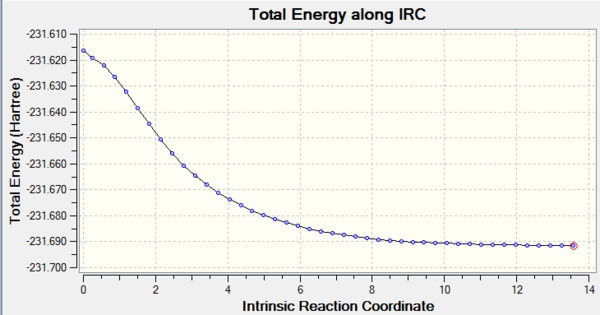
The Intrinsic Reaction Coordinate method allows us to follow the minimum energy path from the transition structure to the local minimum on a potential energy surface. This allows us to work around the difficulty of predicting the conformers produced form the transition structures.

The minimum produced by this method looks most like the Gauche 2 conformer, which indicates it is unlikely to be the actual minimum if we consider the energy calculations from the previous exercise.

This transition structure's IRC did not reach a minimum though did reach a plateau. To find the geometry at the minimum we should run an optimization on the lowest energy structure produced by the IRC.

Nf710 (talk) 17:20, 1 December 2015 (UTC) if you calculate force constants at every step you should have got the true minimum. however you could have optimised this to see if the energy corresponded to your prediction. however you have given a well argued explanation so will give you the marks.

Activation Energies

To be able to consider more thoroughly which transition state is preferred, we look for which has the lowest activation energy. To do this, we analysed both transition structures at both the Hartree Fock 3-21G level of theory and the B3LYP 6-31G*ː

Transition Structureː Method	Structure	Length C1-C2 (Å)	Length C1-C4 (Å)	Angle C1-C2-C3 (°)	Single Negative Frequency (cm-1)
Boatː Hartree Fock		1.381	2.140	121.69	-839.96
Boatː B3LYP		1.392	2.223	122.40	-504.56
Chairː Hartree Fock		1.405	1.986	120.15	-571.91
Chairː B3LYP		1.407	2.037	120.98	-564.99

For the chair and boat structures we find a transition structure (as shown by the single negative frequency found) using each method. It is interesting to see that there is significantly more variation between the results by using the different methods for the chair structure compared to the boat structure.

Nf710 (talk) 18:03, 1 December 2015 (UTC) You must have got confused here because you have already stated that the chair is at ~ -818 cm^-1, good comparrison of geoms however

Using the activation energies for these transition structures, the energies for each transition state at each level of theory were foundː

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619401	-231.466703	-231.461343	-234.516975	-234.430423	-234.424452
Boat TS	-231.602814	-231.450928	-231.445270	-234.493093	-234.351380	-234.345065
Reactant (anti2)	-231.642184	-231.534799	-231.525842	-234.611720	-234.420765	-234.410849

Where 1 hartree = 627.509 kcal mol^-1

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	46.54	44.57	33.82	32.98	33.5 ± 0.5
ΔE (Boat)	52.63	50.56	43.54	41.28	44.7 ± 2.0

Nf710 (talk) 18:10, 1 December 2015 (UTC) Your chair and boat energies are wrong here at B3LYP you must have used a slight incorrect basis set possibly 6-31g**

As expected, the higher level of theory, DFT, gives a closer to literature value that the Hartree Fock method. Energies clearly change a lot more than geometries when using different basis sets for analysis which should be borne in mind when running simulations. Comparing between temperatures, 0K has the higher activation energy. This is expected as there is less energy in the system available to aid the reaction reach the energy barrier. Since the chair transition state has the lower activation energy we can assume this will be the preferred transition structure.

Nf710 (talk) 18:10, 1 December 2015 (UTC) good comparison of energies at 0K and 298K.

Nf710 (talk) 18:10, 1 December 2015 (UTC) This part of the report is good, you have shown a decent understanding of the theory and done what has asked of you, you even went beyond the script with things like the MOs etc.

Diels Alder Cycloadditions

Ethylene and cis-Butadiene

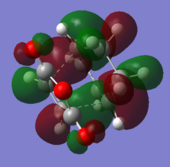
The Diels Alder reaction is a widely used, important cyclisation reaction that we will study the transition state of using a simulation. In this exercise the diene and dieneophile we have chosen to study reacting are cis-butadiene and ethylene. GassView was used to build cis-butadiene and ethylene. Both molecules had their geometry optimised using the Hartree-Fock 3-21G level of theory. Ethylene once optimised was found to have a D2h symmetry, and cis-butadiene was found to have C2v symmetry. The optimised structures allow us to view the HOMO and LUMO of each molecule as shown below:

(Why did you use HF? Tam10 (talk) 12:51, 26 November 2015 (UTC))

cis-Butadiene LUMO Symmetric to the plane	cis-Butadiene HOMO Anti-symmetric to the plane

Ethylene LUMO Anti-symmetric to the plane	Ethylene HOMO Symmetric to the plane

We will calculate the transition structure using the QTS2 method. The input reaction and product molecules submitted were as followsː

And the labelled transition shows as:

(This is not the TS. Looking at the bond lengths below, it looks like the product. Above, it appears that you've performed the QST2 method incorrectly. Gaussian ignores the "bond types" that are created in Gaussview. They are only there for the purpose of the very basic forcefield calculation involved in "cleaning" the structure Tam10 (talk) 12:51, 26 November 2015 (UTC))

With bond lengths:

Bond	Length Å
C1-C2	1.514
C1-C12	1.317
C12-C14	1.514
C14-C9	1.547
C9-C6	1.554
C6-C2	1.564

The use of the QTS2 method means that the bond lengths within the transition structures are very close to the values of the end product.

Orbital comparison

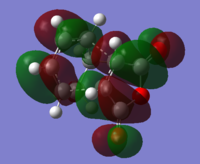
The HOMO and LUMO of the transition state are shown below. It is confirmed as the transition structure by the presence of a single negative frequency. In the transition structure we can see mixing of the HOMO and LUMO of the reactants, showing that this reaction is likely to be favourable. Because the reaction proceeds via Woodward Hoffman rules, we see further evidence that the reaction follows an allowed pathway via the symmetry of the transition state with zero antarafacial components and one suprafacial ocomponent.

Cyclohexene LUMO	Cyclohexene HOMO

(This is confusing, as here you have the correct orbitals. This and that the bond lengths (estimating from these images) look correct suggest you have the right TS now. Did you take the wrong file for the above section? Tam10 (talk) 12:51, 26 November 2015 (UTC))

(What was the imaginary frequency? How did it compare to the lowest positive frequency? And where is the animation for the imaginary frequency? This would also be easier if you uploaded the log files so I could tell what happened Tam10 (talk) 12:51, 26 November 2015 (UTC))

Cyclohexa-1,3-diene and Maleic Anhydride

The favoured product in most Diels Alder reactions is the Endo structure. In this exercise we will analyse the orbitals of two reactants to determine how true this is and why. The transition structures were modeled using the QTS2 method, under the Hartree Fock 3-21G level of theory.

Maleic Anhydride LUMO	Maleic Anhydride HOMO

Cyclohexa-1,3-diene LUMO	Cyclohexa-1,3-diene HOMO

The exo and endo transition structures were confirmed by a single negative vibration, structures shown belowː

Conformer	Transition Structure	HOMO	LUMO
Exo
Endo

(The endo TS here looks quite odd. It might be a single bond-forming TS, but I can't tell without a log file or an illustration of the vibration. I can imagine the comparison of energies would be vastly different as a result Tam10 (talk) 12:51, 26 November 2015 (UTC))

This data seem to show a lot more strain in the formation of the endo form than the exo which is not the expected result as generally the endo product is favoured in Diels Alder reactions. We can however still see that there is better orbital overlap in the endo form which may explain why it is still more favoured in experimental conditions.

The theory relating to the study of orbitals here suggests that there may be a secondary orbital overlap effect which further stabilises the endo form. Unfortunately, this is not an effect that can easily be seen from this level of theory.

(This is not a sufficient explanation. You should show what you mean Tam10 (talk) 12:51, 26 November 2015 (UTC))

Conclusion

Having run a variety of simulations at the two levels of theory (Hartree Fock 3-21G and B3LYP/6-31G*) we can now consider them for their computational ability. The Hartree Fock method generally provides a relatively easy, low computationally expensive method to study a simulation. The B3LYP/6-31G* method provides a better optimisation of a molecule but is generally more computationally expensive and so is perhaps more useful to re-optimise a structure after it has been optimized by the Hartree Fock method first. It is of particular use if the Energy of the system is of significant importance, as this value is more dependent on the basis set used than the geometry.

The use of Frontier Molecular Orbital theory was used to study the Diels Alder reaction and make deductions about likely reaction outcomes. This method allows for interesting discussion but did not seem particularly accurate at the Hartree Fock level of theory.

Using Gaussian to study transition structures has been shown to be a powerful tool in understanding complex systems.