Rep:Mod:ad5215TS
Introduction
The aim of this lab is to investigate three Diels-Alder reactions by considering primary and secondary orbital interactions and the effect these have on the overall energy of the molecules and the transition states. A transition structure is the highest energy point on a reaction energy profile, while on a potential energy surface (PES) it appears as a saddle point. The first derivative of a saddle point is zero - however, the same is true for a minimum or a maximum. In order to establish a saddle point, the second derivative matrix (Hessian matrix) is needed. The Hessian matrix is related to the force constants of the TS vibrations. In the case of a saddle point the determinant of this matrix must be negative, which requires a negative force constant and therefore an imaginary vibration associated with it. A TS optimisation locates this saddle point in 3N-6 dimensions (where N is the number of atoms in the molecule) using various methods (e.g. Hartree-Fock, Density Functional Theory, hybrids of these). An Intrinsic Reaction Coordinate (IRC) calculation can then be used to find the 1D reaction energy profile.[1]
Nf710 (talk) 10:49, 15 December 2017 (UTC) Using the determinant method is a way, but this will also be true if the is an odd number of negative eigenvalues. So you should use the eigenvalues of the hessian generally. A diagram of the PES would have made this paragram much easier to understand.
The methods used in this lab for optimising to a minimum or a TS and for IRC calculations are PM6 and B3LYP. PM6 is a semi-empirical method, i.e. a simplified version of the Hartree-Fock method.[2] B3LYP is a hybrid functional, meaning it employs both the DFT and Hartree-Fock methods. In this case, it was run using a 6-31G basis set.[3]
Nf710 (talk) 10:49, 15 December 2017 (UTC) You have shown some understanding but this is extremely brief.
Exercise 1: Diels-Alder reaction of butadiene and ethylene
(Fv611 (talk) Very good, concise section. Your MO diagram is great. The only thing missing is an assessment of the significance of the measured lengths for the bonds being formed at the TS with respect to the VdW radius of carbon and to the length of an sp3 hybridised bond.)
Butadiene and ethene react in a [4+2] cycloaddition (a Diels-Alder reaction) to yield cyclohexene. In this particular reaction, the diene is more electron-rich than the dienophile, meaning it obeys normal electron demand.[4]
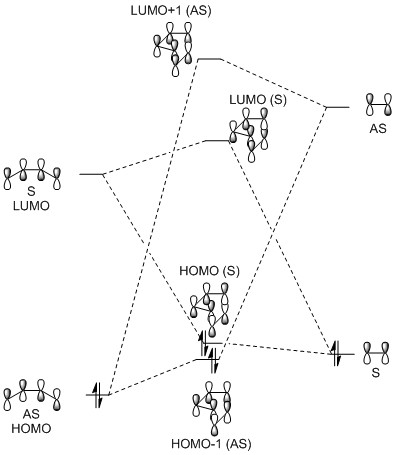
Molecular Orbitals
The MO diagram associated with this Diels-Alder reaction is below, followed by Jmol objects illustrating the MOs. The two non-bonding MOs of butadiene were left out to make the diagram more clear. One thing to note is that this diagram was constructed using the relative energies calculated by Gaussian for the MOs of the transition state and not of the products. This is why the resulting MOs are higher in energy than would be expected.
Butadiene
|
|
Ethene
|
|
Diels-Alder Transition State
|
|
|
|
In order for orbitals to have a favourable interaction, i.e. one that results in overall stabilisation of the molecule, the overlap integral associated with that interaction must be non-zero. Since this integral is proportional to the spatial overlap of the orbitals, these must have the same symmetry — both symmetric (S) or both antisymmetric (AS). This results in an overall symmetric function, with a non-zero overlap. Combining orbitals of opposing symmetries (i.e. an AS and an S) leads to an antisymmetric function and to a zero overlap integral.[5]
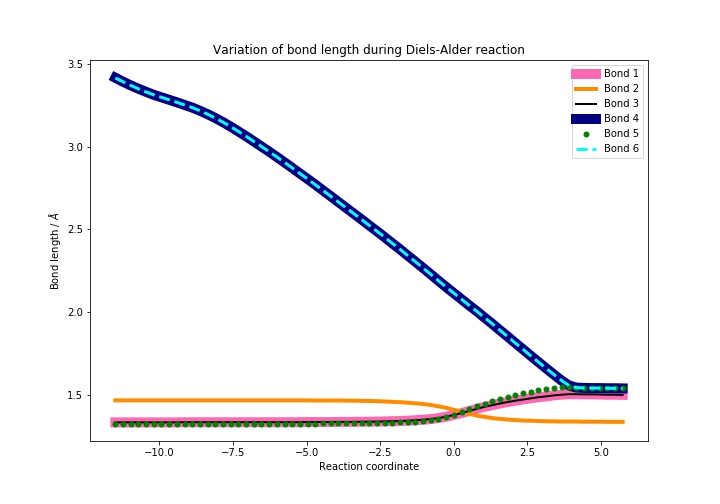
Bond lengths
This reaction is a [4+2] cycloaddition (specifically a Diels—Alder reaction). It proceeds via a cyclic transition state and it involves the breaking of three C-C double bonds and the formation of two single bonds and a new double bond.[4] The lengths of these bonds are expected to change accordingly during the course of the reaction.
Average C-C bond lengths are 1.530 Å for an sp3-sp3 single bond, 1.507 Å for an sp3-sp2 single bond, 1.460 Å for an sp2-sp2 single bond and 1.316 Å for an sp2-sp2 double bond.[6] The van der Waals radius of a carbon atom is 1.70 Å.[7] The bond lengths present in the reactants / products during the course of the reaction are in Table 1, below. They differ from the literature values by roughly 0.01 Å. However, literature values for C-C bond lengths in cyclohexene are almost identical to the calculated ones: 1.541 Å for an sp3-sp3 single bond, 1.506 Å for an sp3-sp2 single bond, and 1.326 for an sp2-sp2 double bond.[6] The double bond is, in fact, longer in the optimised product than in the literature example - this could be due to the fact that the product was optimised at the PM6 level. Using a more accurate method could result in a value more closely matched to literature.
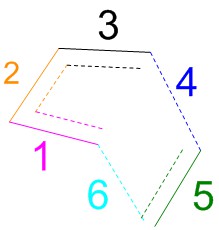
| Bond | Bond length / Å | ||
|---|---|---|---|
| Reactants | Transition state | Products | |
| Bond 1 | 1.335 | 1.380 | 1.501 |
| Bond 2 | 1.468 | 1.411 | 1.338 |
| Bond 3 | 1.335 | 1.380 | 1.501 |
| Bond 4 | 3.415 | 2.115 | 1.540 |
| Bond 5 | 1.327 | 1.382 | 1.541 |
| Bond 6 | 3.414 | 2.115 | 1.540 |
Bonds 4 and 6 form during the reaction, so they "shorten" (it can be assumed that the reactants are infinitely apart to begin with, so the initial bond length is infinite. In the calculation, the reactants are brought closer together in order for the reaction to happen, so the initial bond length is less than infinity, but still considerably larger than the final length). Bond 2 changes from a single bond to a double bond and will therefore shorten as well. It should be noted that the pi-system in butadiene is conjugated. Therefore this bond has some double bond character and is shorter than the average C-C single bond. Bonds 1, 3 and 5 are all double bonds in the reactants and single bonds in the product, so they will become longer (1 and 3 are identical in this case and the plots overlap).
The vibration corresponding to the formation of the transition state (and the formation of the new bonds) is below. The two bonds are shown to form at the same time, which agrees with the fact that a Diels-Alder reaction proceeds via a concerted mechanism (i.e. synchronous breaking and forming of bonds).[4]
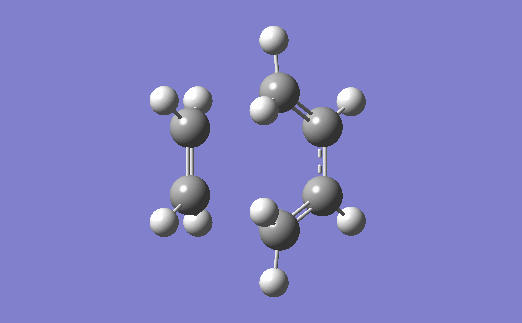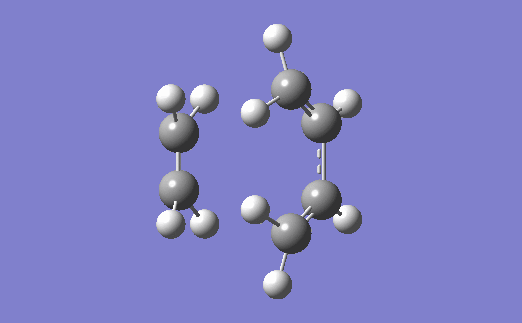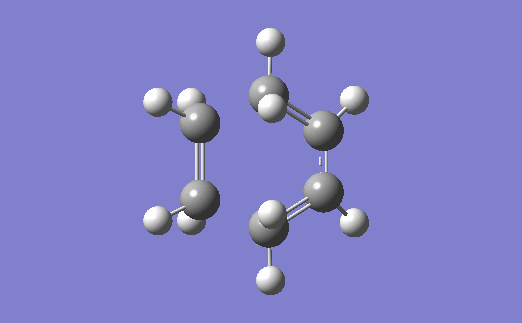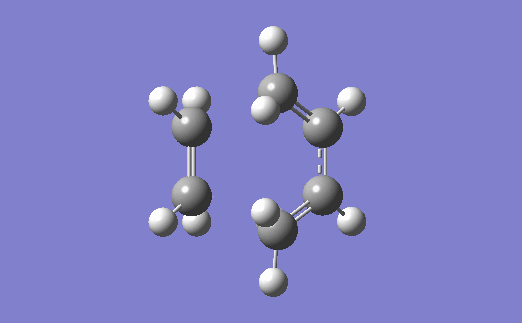
Relevant files
Optimised product (PM6): File:Ad5215 ex1 PDT OPT.LOG
Diels-Alder IRC: File:Ad5215 ex1 IRC.LOG
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
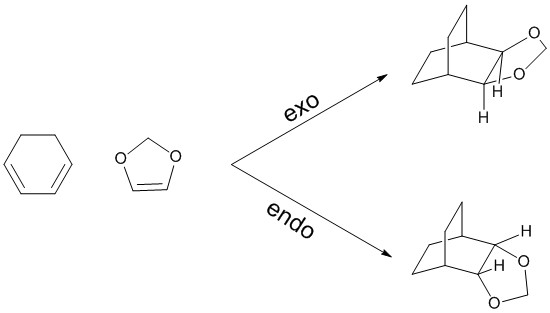
Cyclohexadiene and 1,3-dioxole can undergo a [4+2] cycloaddition. Because the double bond in the dienophile (i.e. the dioxole) is substituted, the reaction can yield two different products, depending on the orientation of the molecules when approaching each other. The exo product is formed when the substituents of the dienophile are pointing away from the pi system in the diene, while the endo is formed when the dienophile has the opposite orientation.[4]
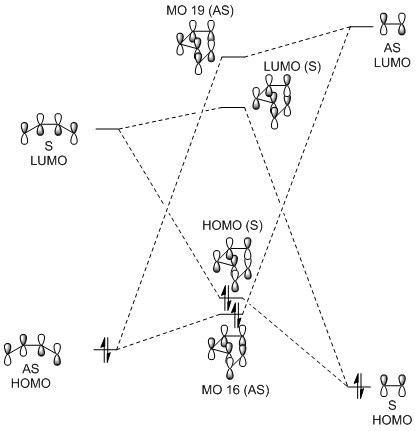
Molecular Orbitals
(Fv611 (talk) The MO diagram is overall good, but the dienophile LUMO is a bit lower in energy than what I would have expected for an inverse electron demand reaction. You also should have discussed the difference between the endo and exo MO relative energies. As a rule of thumb, if you are not drawing the full molecules on your MO diagram, you need to specify which one is the diene and which one the dienophile.)
The MO diagram for this reaction is below, as well as Jmol objects of the transition state MOs for both the endo and exo products. Due to the electron-donating oxygen atoms which make the dienophile more electron rich, this Diels-Alder reaction obeys inverse electron demand.[4] As with exercise 1, the MO energies are those corresponding to the transition state (calculated by running an IRC, followed by an Energy calculation in Gaussian). The reactants, products and transition states were optimised at the B3LYP level while the IRCs were run at the PM6 level.
10:58, 15 December 2017 (UTC) You can see this qualitatively if you look at the MOs of the diagram But if you looks at the MOs of the reactants on the same PES you can also see it qualitatively.
Endo TS
|
|
|
|
Exo TS
|
|
|
|
Energies
| Product type | Reaction barrier | Reaction energy | ||
|---|---|---|---|---|
| Hartrees/particle | kJ/mol | Hartrees/particle | kJ/mol | |
| Endo | 0.058218 | 152.85133794 | -0.027385 | -71.89930759 |
| Exo | 0.061152 | 160.55455388 | -0.026056 | -68.41001858 |
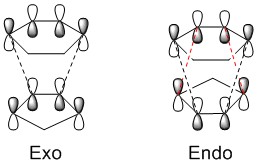
The energy barrier refers to the difference in energy between the reactants and the transition state. Essentially, it is the energy needed for the reaction to happen. It can be seen from the table above that this barrier is greater in the case of the exo transition state. This means that the endo product is kinetically preferred, as it will overcome this energy requirement more easily and be formed faster. This is because in the case of the endo product the transition state is stabilised by favourable interactions between the oxygen atoms in the 1,3-dioxole and the π-system of the cyclohexadiene. This secondary orbital overlap is shown on the right and is also visible in the Jmol images above.[4]
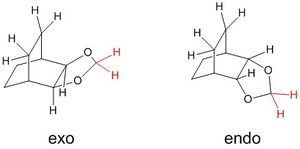
The endo product is also the thermodynamically preferred product - the free energy difference (between products and reactants) associated with the reaction is smaller (more negative) for the endo product. In the exo product the five-membered ring is oriented in a way that results in steric clash between the CH2 fragment (coloured in red in the figure) and the carbon "bridge". This interaction is not as significant in the endo product, since the CH2 fragment is farther away. Therefore, the endo product will be lower in energy than the exo.
This is in accordance with the endo rule, which states that in [4+2] cycloadditions the endo product is preferred due to the favourable secondary orbital overlap which stabilises the transition state (meaning the endo product is favoured kinetically). This is true even if the exo product is thermodynamically more stable.[4]
Relevant files
Cyclohexadiene (B3LYP): File:Ad5215 CYCLOHEXADIENE B3LYP.LOG
1,3-Dioxole (B3LYP): File:Ad5215 13 DIOX BLYP.LOG
Endo product (B3LYP): File:Ad5215 ENDO PRODUCT B3LYP.LOG
Exo product (B3LYP): File:Ad5215 EX2 EXO PDT B3LYP.LOG
Endo IRC (PM6): File:Ad5215 ex2 ENDO IRC.LOG
Exo IRC (PM6): File:Ad5215 ex2 EXO IRC.LOG
Nf710 (talk) 11:01, 15 December 2017 (UTC) This was a good section. You could have talked abit more about the electron demand of the reaction. Your energies are slightly not correct but you have come to the correct conclusions and you have used diagrams to explain them which is good. Your intro could have gone into more depth.
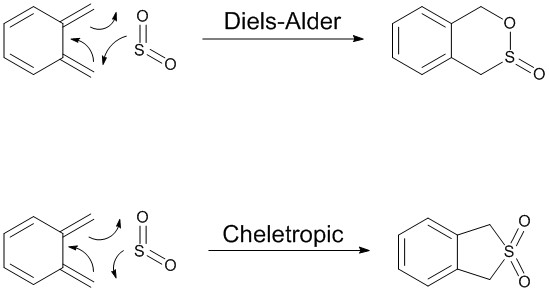
Exercise 3: Reaction between o-xylylene and SO2
o-Xylylene and sulfur dioxide can react in multiple ways. The two conjugated double bonds on the 6-membered ring act in a similar way to butadiene. Therefore, the two molecules can either undergo a [4+2] cycloaddition, resulting in two Diels-Alder products (endo and exo) or can react in a cheletropic manner, forming a 5-membered heterocycle. IRC calculations were run for all three possible outcomes of the reaction (Diels-Alder, endo and exo, and cheletropic). These are reproduced below as .gif files.
| Endo | Exo | Cheletropic |
|---|---|---|
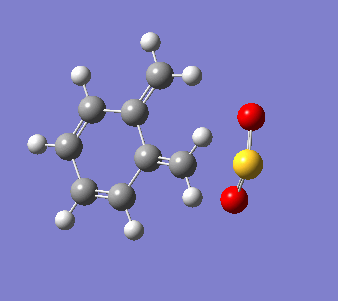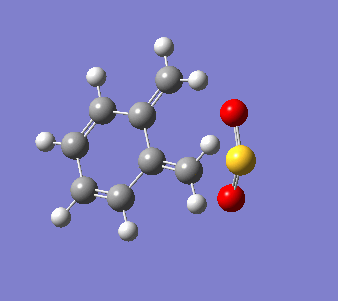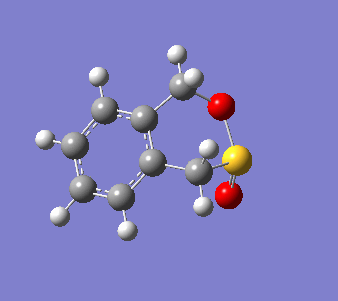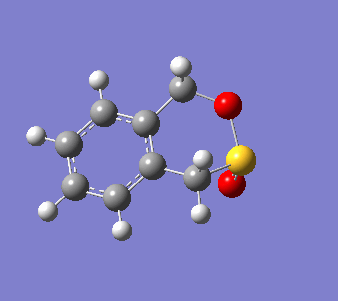
|
|
|
The free energies calculated by Gaussian were tabulated (using the reactants/products/transition states optimised at the PM6 level). Activation energies and free energy changes were calculated for each reaction and energy profiles were plotted using Python and Jupyter.
| Product type | Reaction barrier | Reaction energy | ||
|---|---|---|---|---|
| Hartrees/particle | kJ/mol | Hartrees/particle | kJ/mol | |
| Endo | 0.031742 | 83.33860952 | -0.037124 | -97.46904857 |
| Exo | 0.033259 | 87.32149247 | -0.037365 | -98.10179398 |
| Cheletropic | 0.040243 | 105.65798194 | -0.058821 | -154.43451422 |
Based on the thermodynamic calculations above, the endo Diels-Alder product is the kinetically preferred product (smallest activation energy), with the exo Diels-Alder having a slightly higher barrier. The cheletropic product has a much larger activation energy, but is much more stable - this is the thermodynamic product. The free energy change corresponding to the cheletropic reaction is almost 60 kJ/mol greater than for the Diels-Alder reaction. This is summed up in the graph below, which shows the reaction energy profile for the formation of both Diels-Alder products, as well as for the cheletropic reaction. These reactions are all favourable from a thermodynamic point of view, which can be explained by the fact that the end product in all cases is an aromatic molecule, essentially a substituted benzene ring. Aromatic stabilisation is larger than stabilisation given purely by conjugation of double bonds, which leads to a lower energy of the molecule.[4]
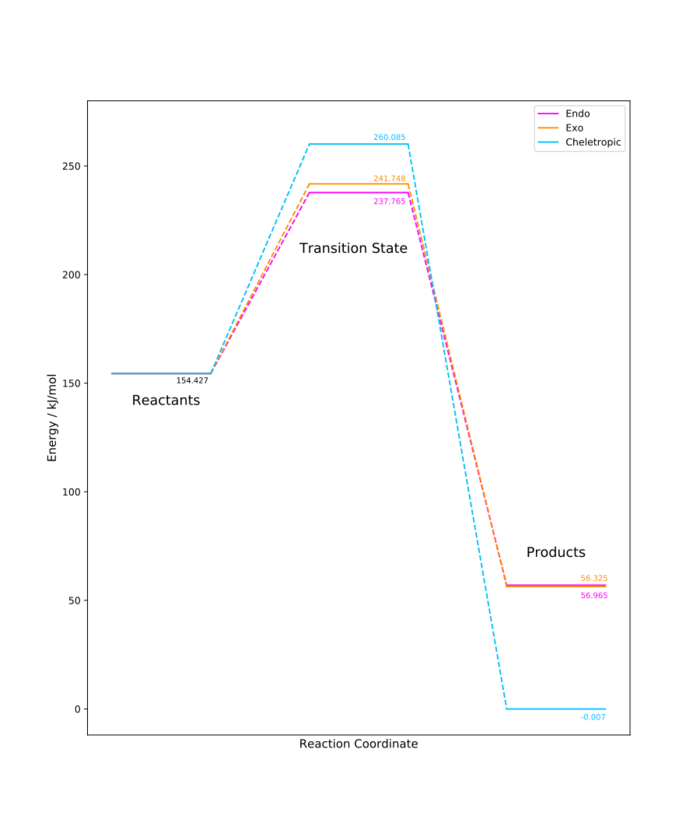
(Normalising the reactants to 0 would allow easier comparison and faster visualisation of barriers and reaction energies. Otherwise, nice plot. Python > Excel Tam10 (talk) 14:46, 7 December 2017 (UTC))
The o-xylylene molecule has another site which can act as a diene in a Diels-Alder reaction. The "exocyclic" reaction site is the one that was previously considered in all the calculations and involves the double bonds outside the 6-membered ring. The "endocyclic" site is the cyclohexadiene fragment present in the molecule. The endo and exo products and transition states for reactions at the "endocyclic" site were optimised and the energies tabulated.
| Product type | Reaction barrier | Reaction energy | ||
|---|---|---|---|---|
| Hartrees/particle | kJ/mol | Hartrees/particle | kJ/mol | |
| Endo | 0.043252 | 113.55811036 | 0.006793 | 17.83501904 |
| Exo | 0.046236 | 121.39260128 | 0.008486 | 22.27998993 |
The plot below shows these reactions profiles and allows for them to be compared with the reactions at the "exocyclic" site. It can be seen that reactions at this site are less favourable, both thermodynamically (the products are higher in energy) and kinetically (the transition states are highest in energy and therefore the activation barriers are the greatest).
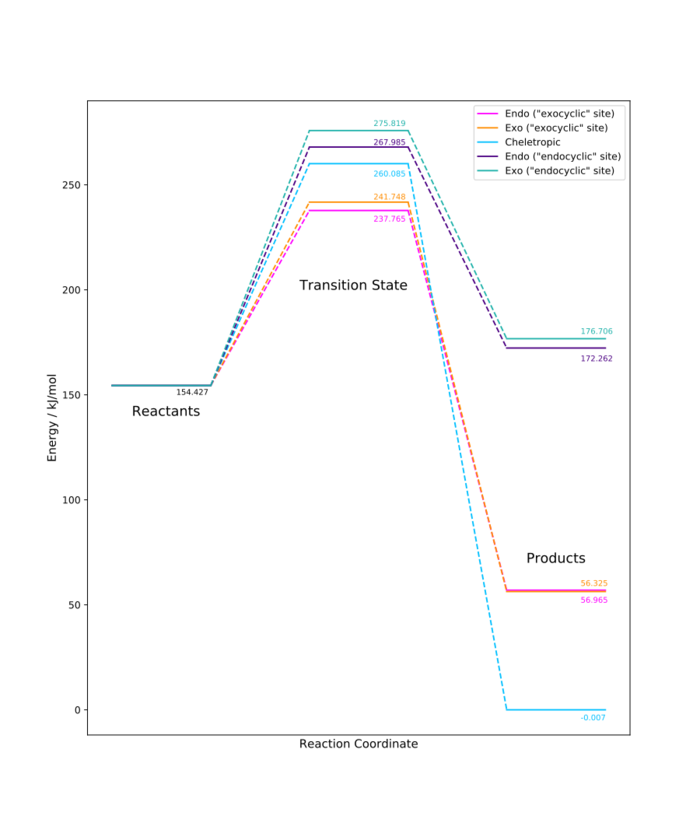
Relevant files
Xylylene: File:Ad5215 ex3 XYLYLENE pm6.LOG
SO2: File:Ad5215 ex3 SO2 pm6.LOG
"Exocyclic" DA endo TS: File:Ad5215 ex3 DA ENDO TS PM6.LOG
"Exocyclic" DA endo IRC: File:Ad5215 ex3 DA ENDO IRC.LOG
"Exocyclic" DA endo product: File:Ad5215 ex3 Pdt endo min.LOG
"Exocyclic" DA exo TS: File:Ad5215 DA EXO TS PM6.LOG
"Exocyclic" DA exo IRC: File:Ad5215 ex3 DA EXO IRC.LOG
"Exocyclic" DA exo product: File:Ad5215 ex3 PRODUCT EXO PM6.LOG
Cheletropic TS: File:Ad5215 CHEL TS PM6.LOG
Cheletropic IRC: File:Ad5215 ex3 chele IRC.LOG
Cheletropic product: File:Ad5215 ex3 chele PRODUCT MIN.LOG
"Endocylic" DA endo TS: File:Ad5215 extra ENDO TS.LOG
"Endocylic" DA endo product: File:Ad5215 ex3 extra PM6 PDT endo.LOG
"Endocylic" DA exo TS: File:Ad5215 ex3 extra EXO TS.LOG
"Endocylic" DA exo IRC: File:Ad5215 ex3 extra EXO IRC.LOG
"Endocylic" DA exo product: File:Ad5215 ex3 extra EXO PDT PM6.LOG
All optimised at the PM6 level.
Conclusion
The results obtained in this lab agree with pre-existing theory (in this case, the endo rule). While they require some knowledge of the reactants or products and in some cases of the transition state, computational methods prove to be a useful and welcome addition to more traditional chemical procedures, allowing for a detailed and (if using an appropriate method and basis set) accurate analysis of reaction parameters (such as energies and pathways) as well as visualisation of molecular orbitals. In the case of o-xylylene, for example, it was possible to model and analyse three different reactions and determine their outcome, while in practice this would be much more difficult, as this substrate is highly unstable in the solid or liquid phases.[8]
Computational chemistry could be used to predict the outcome of reactions before attempting these in practice, therefore reducing the cost and time spent. It can also be used in conjunction with "classical" chemical methods to improve understanding of reaction mechanisms and pathways.
References
- ↑ Gaussian – Vibration Analysis in Gaussian, http://gaussian.com/vib, (accessed December 2017)
- ↑ Gaussian – Semi-Empirical Methods, http://gaussian.com/semiempirical, (accessed December 2017)
- ↑ Gaussian – Density Functional (DFT) Methods, http://gaussian.com/dft, (accessed December 2017)
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, 2nd edn., 2012.
- ↑ P. Atkins, T. Overton, J. Rourke, M. Weller and F. Armstrong, Shriver & Atkins’ Inorganic Chemistry, Oxford University Press, 5th edn., 2010.
- ↑ 6.0 6.1 A. G. Orpen, L. Brammer, F. H. Allen, O. Kennard, D. G. Watson and R. Taylor, J. Chem. Soc. Dalt. Trans., 1987, S1–S83.
- ↑ F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry Part A: Structure and Mechanisms, 2007.
- ↑ R. D. Miller, J. Kolc and J. Michl, J. Am. Chem. Soc., 1976, 98, 8510–8514.