Jump to content

Rep:Mod:abcmod3

From ChemWiki

Year 3 Computational Lab Alex Cook 00555113

Module 3: Transition States and Reactivity.

This experiment involves the study of transition states, specifically the transition states involved in the Cope rearrangment and the Diels-Alder reaction. Changes in electron distribution and bonding type mean that Classical formulae cannot be used as they do not describe bonds being made and broken. Thus a new technique is needed. We will use computational techniques including using Gaussian[1] for molecular orbital-based methods and numerical solving of the Schrodinger equation. This allows us to locate and identify structures of Transition States, find reaction paths and determine barrier heights by using potential energy surfaces.

Tansition State theory was developed as early as 1935 by Eyring and by Evans and Polanyi.[2] The theory is based on a few assumptions. Firstly, the Born-Oppenheimer approximation is assumed, which in basic terms, allows the wavefunction of a molecule to be broken into its electronic and nuclear components, but in reality there is vibronic coupling. Transition state theory assumes that there is an equilibrium between the products and the transition state, and that once the high point on the Potential energy surface (transition state) has been crossed it cannot be re-crossed. The theory also assumes the reaction system will pass over the lowest energy saddle on the potential energy surface.


The Cope Rearrangement

The rearrangement of 1,5-hexadiene was described by A. Cope in 1940.[3] The mechanism of this [3,3]-sigmatropic shift rearrangment was discussed thouroughly over decades and semiempirical and ab initio electronic structure calculations have been used in an attempt to prove theories. It was debated whether the rearrangment proceded in a concerted, stepwise or dissociative manner.

For example in 1994 David A. Hrovat et Al. investigated whether the rearrangement involves the formation of chair cyclohexane-1,4-diyl as a discrete intermediate or whether the reaction is concerted and passes through a six-electron, aromatic transition state in which bond making and bond breaking are synchronous.[4]

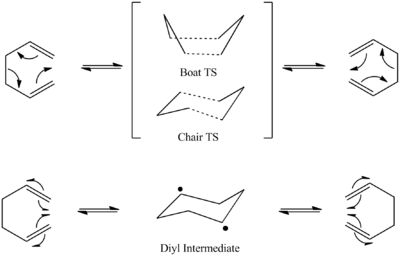
Figure 1: Cope rearrangement schemes


There is a scale of mechanisms between the radical and aromatic pathways, the exact mechanism can depend on the nature and position of the substituents.[5]Tthese days it is generally accepted that the reaction occurs in a concerted fashion via an aromatic chair transition structure. [6]


Reactants and Products

Optimisation

Both gauche and antiperiplanar conformations are possible, as there is rotation about the central sigma bond, which permits interconversion. Thus a dihedral scan could be carried out to asses how the orientation and geometry affects the total energy. The dihedral scan would show that the conformers with groups elapsing are highest energy structures, and that the Gauche and antiperiplanar conformations are represented by the minima.

Below is an example of a dihedral scan for butane from Henrey Rzepa Conformational analysis course notes.[7]

Figure 2: Dihedral scan conformational analysis of butane


The reactants and products (all low energy conformational isomers of 1,5-Hexadiene) were optimised in order to compare their optimised energy and geometries, and thus find the most stable isomers.

Conformer Point Group Total Energy (Hartrees) Relative Energy (Kcal /mol)
Gauche 1 [8] C2 -231.68772 +3.100
Gauche 2 [9] C2 -231.69167 +0.621
Gauche 3 [10] C1 -231.69266 0.000
Gauche 4 [11] C2 -231.69153 +0.709
Gauche 5 [12] C1 -231.68962 +1.908
Gauche 6 [13] C1 -231.68916 +2.196
Anti 1 [14] C2 -231.69260 +0.038
Anti 2 [15] Ci -231.69254 +0.075
Anti 3 [16] C2h -231.68907 +2.253
Anti 4 [17] C1 -231.69097 +1.060
Figure 3: Comparison of Energy of optimised(HF/3-21G level) structures of 1,5 hexadiene conformers


We would possibly expect that an antiperiplanar conformation would have the lowest energy, due to favourable alignment of σ and σ* orbitals, and least Pauli repulsions (or steric clash) disfavoring any eclipsed orientations. However from the above calculations we can see that the gauche3 conformer is the most stable, with Anti1 and Anti2 being the next most stable.

This could be due to Van der Waals forces which operate at longer range than the other two effects. This effect is highly dependent on the functional groups on either side of the C-C bond. However it could also be due to the fact that the 3-21G basis set is not the most accurate.

Thus the three most stable conformers calculated at the HF/3-21G level were the optimised again but using the higher level basis set DFT/ 631-G*.

Conformer Point Group Total Energy (Hartrees) Relative Energy (kcal/mol) Newman Projection
Anti 1 [18] C2 -234.611800 0
Anti 2 [19] Ci -234.611710 + 0.057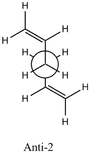
Guache 3 [20] C1 -234.611329 + 0.296
Figure 4: Comparison of Energy of optimised(DFT/6-31G* level) most stable 1,5 hexadiene conformers


Now the lowest energy conformer has been calculated to be the anti 1 conformer, closely followed by anti 2. This is what would have been origionally expected.


Frequency Analysis

Frequency analysis was carried out on the 3 most stable conformers at the B3LYP/6-31G level to confirm that a minimunm in energy has been found and that the sturcture had been optimised.

For conciseness the most important stretches, rather than all 42 distinct positive vibrational modes, have been compared below.

Conformer Symmetrical C=C Stretching mode / cm-1 Asymmetrical C=C Stretching mode / cm-1
Anti 1 [21] 1731 [4.69] Animation 1734 [13.54] Animation
Anti 2 [22] 1731 [0.00] Animation 1734 [18.13] Animation
Gauche 3 [23] 1732 [6.88] Animation 1733 [6.13] Animation
Figure 5: Frequency analysis(DFT/6-31G* level) most stable 1,5 hexadiene conformers

literature values for experimental results have the C=C bond vibrational frequency at are around 1650cm-1.[24] This is in not in great agreement, however it is not bad considering the literature values do not distinguish between different conformations as the rotations are faster than the timescale for IR spectroscopy.

The differences in symmetry in the conformers can be appreciated as it leads to the different intensity absorptions seen.

Thermochemical Analysis

Thermochemical data was obtained from the log file from the frequency analysis of the anti 1 conformer.[25] Thermochemical information was then found for absolute zero by adding the keywords "freq=readisotopes" to the input file,[26] so we can compare 0K and 298K.

0K 

Zero-point correction=                           0.142930 (Hartree/Particle)
 Thermal correction to Energy=                    0.142930
 Thermal correction to Enthalpy=                  0.142930
 Thermal correction to Gibbs Free Energy=         0.142930
 Sum of electronic and zero-point Energies=           -234.468861
 Sum of electronic and thermal Energies=              -234.468861
 Sum of electronic and thermal Enthalpies=            -234.468861
 Sum of electronic and thermal Free Energies=         -234.468861

298.15K 

Zero-point correction=                           0.142515 (Hartree/Particle)
 Thermal correction to Energy=                    0.149836
 Thermal correction to Enthalpy=                  0.150780
 Thermal correction to Gibbs Free Energy=         0.111639
 Sum of electronic and zero-point Energies=           -234.469285
 Sum of electronic and thermal Energies=              -234.461964
 Sum of electronic and thermal Enthalpies=            -234.461020
 Sum of electronic and thermal Free Energies=         -234.500162

This Thermochemical analysis shows that the energy sums for the conformer are the same in the 0K calculation. This is expected as no energy contributions come from thermal contributions at 0K. Also, moving from 0k to 298K the the sum of electronic and thermal free energies becomes more negative. This can be rationalised using the Gibbs free energy equation (G= H - TS) as temperature is increased the entropy term also increases.

Transition States

Now we have knowledge of the stable conformers of the reactancts and products wee can optimise the transition state structures to gain a complete understanding of the Cope rearrangement.

Optimisting the Chair Transition State

Firstly, a 'best guess' for a chair transition state was made be placing two optimised allyl fragments in the appropriate arrangement and roughly 2.2Å apart, this allows the fragments to approach each other in a 'chair-like' manner. The fragments in this arrangement were then optimised to a TS using the Berny algorithim and HF/3-21G level basis set.[27] the Force constant was calculated once at the begining, and the keywords "opt=noeigen" was used with the aim of stopping the calculation from terminating if more than one imaginary frequency is found. 

Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/MOdule3/cope/cyclohexane/abc_chair_ts_optfreq.fchk

abc_chair_ts_optfreq
File Name = abc_chair_ts_optfreq
File Type = .fch
Calculation Type = FREQ
Calculation Method = RHF
Basis Set = 3-21G
Charge = 0
Spin = Singlet
Total Energy = -231.61932231 a.u.
RMS Gradient Norm = 0.00005330 a.u.
Imaginary Freq =
Dipole Moment = 0.0003 Debye
Point Group =

Item               Value     Threshold  Converged?
 Maximum Force            0.000078     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.001389     0.001800     YES
 RMS     Displacement     0.000223     0.001200     YES
 Predicted change in Energy=-1.680084D-07
 Optimization completed.
    -- Stationary point found.

A of the optimised chair transition state, with measurement annotations, is provided.

Figure 6: Chair transition state imaginary frequency animation


This allyl fragment transition structure was then optimised again using the frozen coordinate method. This involves setting redundant coordinates. The distance between the terminal allyl fragment carbon atoms is set to exactly 2.2Å, and the fragments are optimised using the additional keyowrds "opt=modredundant".[28]


Optimisation of the Boat Transition State

This was done by the quadratic synchronous transit QST2 method, where thre reactant and product were specified ( from previously calculated 1,5 hexadienes) and Gaussian calculates the Transition State for the reaction. Gaussian assumes the coordinates of the atoms in the transition structure will lie along a parabola connecting the reactant and product geometries. This involved numbering the atoms in the correct order co the calculation could procede.

The first optimisation using this method failed to complete.[29] The parameters entered meant that gaussian simply translated one of the fragments not taking into accoun rotation around the central bonds.

Figure 7: Boat transition state failed optimisation atom labelling

A of the failed optimisation of boat transition state, with measurement annotations, is provided.


The central dihedral angle was then set to 0 degress. and adjacent bond angles set to 100 degrees. This means the reactants and products start at a geometry that is more similar o the boat transition state, and the optimisation completes.[30] 

Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/MOdule3/cope/cyclohexane/boat/abc_boat_optqst2_refined.fchk

abc_boat_qst2_refined
File Name = abc_boat_optqst2_refined
File Type = .fch
Calculation Type = FREQ
Calculation Method = RHF
Basis Set = 3-21G
Charge = 0
Spin = Singlet
Total Energy = -231.60280243 a.u.
RMS Gradient Norm = 0.00002001 a.u.
Imaginary Freq = 1
Dipole Moment = 0.1584 Debye
Point Group =

Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.001486     0.001800     YES
 RMS     Displacement     0.000426     0.001200     YES
 Predicted change in Energy=-6.174014D-08
 Optimization completed.
    -- Stationary point found.
Figure 8: Boat transition state successful optimisation atom labelling


A of the successful optimisation of boat transition state, with measurement annotations, is provided.


Figure 9: Boat transition state imaginary frequency animation


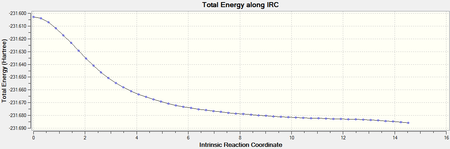
Intrinsic Reaction Coordinate

The intrinsic reaction coordinate method in Gaussian, allows us to determine the minimum energy path folowed from a transition state to the product, or minimum on the PES. This is useful for determining whether a particular transition state actually leads to a desired product, as according to Hammonds Postulate the transition state may resemble the end product, but it is still difficult to determine which conformer forms.

For the first Intrinsic Reaction Coordinate calculated the HF/3-21G method was used, with 50 steps taken anlong the IRC in the forward direction only, with force constants being calculated once at the start. It was terminated after 26 steps.

The calculations were then changed to find viable parameters for it reached completion. The number of points to calculate along the IRC was increased to 150. The calculation then terminated after 26 also.

So now the IRC calculation was re-run specifying calculation of the force constants at every step. This gave acceptable results for both chair and boat conformations. It was determined by visual inspection of the geometries that chair transition state leads to gauche 2 conformer and the boat-like transition state leads to the gauche 3 conformer.

Calculation Transition state Maximum points along the IRC Calculation stopped after (steps) Compute Force Constant Total Energy
1 Chair[31] 50 26 Once -231.61932231
2 Chair[32] 150 26 Once -231.61932231
3 Chair[33] 50 47 Always -231.61932231
4 Boat[34] 50 50 Always -231.60280243
Figure 10: Summary of IRC calculations for cyclohexande transition states


Chair Transition State IRC Boat Transition State IRC
Graph
Graph
Graph
Graph
 Figure 11: Summary of optimised cyclohexane transition state IRC's

Activation Energies

The activation energy or height of the potential barrier separating two minima of potential energy, the reactants and products, can be calculated at 298.15K by subtracting the 'sum of the electronic and thermal energies' of the reactants from that of the transition state. The calculated activation energies proved to be in good agreement with the literature values, particularly for the higher level calculations.

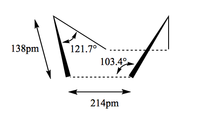
As seen from the geometry comparison in figure 12, the differences in geometry at the two different levels of theory are not that significant, however the difference in energies are more significant.


Chair TS Geometry Boat TS Geometry
3-21G
6-31G*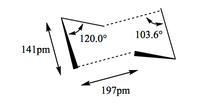
Figure 12: Comparison of geometries of optimised cyclohexane transition states


HF/3-21G B3LYP/6-31G* Literature Activation Energy (kcal/mol)[35]
TS Structure Gauche 3 Sum of Electronic and Thermal Energies (Hartrees) Sum of Electronic and Thermal Energies (Hartrees) ΔE Activation Energy (Hartrees) ΔE Activation Energy (kcal/mol) Anti 1 Sum of Electronic and Thermal Energies (Hartrees) Sum of Electronic and Thermal Energies (Hartrees) ΔE Activation Energy (Hartrees) ΔE Activation Energy (kcal/mol)
Chair -231.521146[36] -231.461339[37] 0.0598070 37.5 -234.461964[38] -234.409010[39] 0.052954 33.2 33.5±0.5
Boat -231.445299[40] 0.0758470 47.6 -234.396006[41] 0.065958 41.4 44.7±2.0
Figure 13: Comparison of Activation Energies of optimised reactants and transitions states


The Diels-Alder Reaction

The Diels-Alder reaction is a [4+2]pi cycloaddition reaction. A conjugated diene reacts with a dienophile which in this case is a double bond, to form an adduct with a 6 membered aromatic ring. Two new sigma bonds are formed athe the expense of two pi bonds in the starting materials.

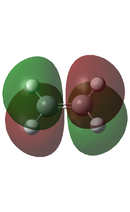
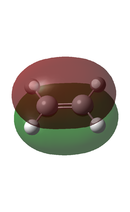
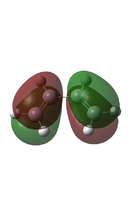
In a typical Diels-Alder, there is an interaction between the HOMO of one fragment and the LUMO of the other to form a new bonding molecular orbital and its corresponding anti-bonding molecular orbital. However, this can only be the case if the HOMO and the LUMO are of the same symmetry, as this allows for required overlap of electron density. Using two Diels-Alder cycloaddition examples below, these orbital interactions will be further analysed, and the molecular orbitals of the transition states will be calculated and visualised.

Butadiene and Ethene Diels-Alder reaction

The first reaction investigated was the Butadiene and Ethene Diels-Alder reaction - the simplest Diels-Alder. Cis-butadiene and ethene, contribute 4pi and 2pi electrons to the reaction each, and form cyclohexene via a 6 membered transition state.

Figure 14: Typical Diels-Alder reaction


Analysis of Reactants

The reactants were first optimised to the B3LYP/3-21G level, and then further to the B3LYP/6-31G level.

The Energy of the optimised s cis conformer was -155.926896 Hartree[42]. And the Energy of the optimised s trans conformer was -155.932441 Hartree[43]. Thus the s trans conformer is favoured due to the less steric hindrance than in the s cis form. Only the s cis form however is able to react with the dienophile ethene, which had a total energy of -78.558415 Hartree.[44]

LUMO HOMO Energy of Optimised Structure (Ha)
Ethene
Antisymmetric
Symmetric		 -78.558415
s cis Butadiene
Symmetric
Antisymmetric		 -155.926896
Figure 15: Summary of MOs and Energy for the optimised(DFT/6-31G* level) Diels-Alder reactants

As previously stated, in order for a Diels-Alder to be allowed, the HOMO and the LUMO have to be of the same symmetry, as this allows for required overlap of electron density. It can be seen that the HOMO of Butadiene and the LUMO of Ethene both have the same antisymmetric symmetry. Also the HOMO of Ethene has the same symmetry as the LUMO of Butadiene, both are symmetric. However as Butadiene is electron rich, it is expected that the interaction is between the HOMO of Butadiene and the LUMO of the electron deficient Ethene.

Analysis of Transition State

Now the Transition state of the reaction was found by arranging the reactants in the appropriate 'guessed' geometry approximately 2.2 Angstrom apart, and then the system was optimised to the DFT/6-31G* level.[45] The Imaginary vibrational mode corresponds to the maxima stationary point and therefore indicates the transition state Structure was found.

LUMO+1 LUMO HOMO HOMO-1 Energy (Ha) Imaginary Vibration Animation Frequency of Vibration (cm-1) Jmol
Antisymmetric
Symmetric
Symmetric
Antisymmetric		 -234.432889
-525.08
Figure 16: Summary of optimised(DFT/6-31G* level) Diels-Alder transition state MOs and properties

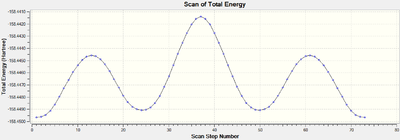
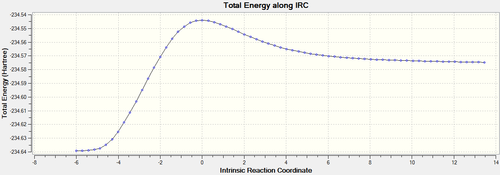
An Intrinsic Reaction Coordinate calculation was carried out.[46] The product, as seen on the left side of the IRC total energy graph, has a lower energy than the reactant indicating that the reaction is thermodynamically favored. The fact that the product formed in the reverse direction means that the transition state comes early on in the reaction and resembles the reactants more than the products.

The animation of the IRC highlights nicely the optimal angle for the Ethene to approach the Butadiene for the reaction to proceed. Here it is calculated to be 102.3°. A more in depth discussion of the geometry of the transition state is below, to provide a comparison for the geometries of the next reaction's Transition States.

Figure 17: IRC animation for Diels-Alder Transition state
Figure 18: IRC total energy graph for Diels-Alder Transition state

Cyclohexadiene and Maleic Anhydride Diels-Alder Reaction

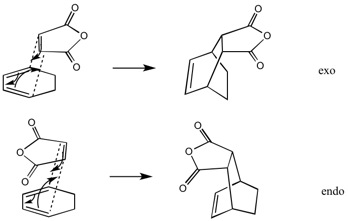
A sometimes useful feature of the Diels-Alder Reaction is it's high steroselectivity. This stereoselectivity is summed up in the 'cis rule' and the 'endo rule'. The cis rule states that the relative stereochemistry of the substituent groups is mantained in the product. The endo rule states that the diene and dieneophile arrange themselves in parralel planes and the most stable transition state is where there is the most possibilty of orbital overlap.[47]

Figure 19: Endo/Exo relationship summary


Analysis of Reactants

The Reactants were optimised at the DFT/6-31G* level. And as with the standard Diels-Alder above the HOMO and LUMO have the required symmetries for the formation of bonding interactions.

LUMO HOMO Energy of Optimised Structure (Ha)
Cyclohexadiene[48]
Symmetric
Antisymmetric		 -233.321026
Maleic Anhydride[49]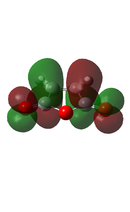
Antisymmetric
Antisymmetric		 -379.262730
Figure 20: Summary of MOs and Energy for the optimised(DFT/6-31G* level) cyclohexadiene and maleic anhydride


Analysis of Transitions States

The optimised reactants were then arranged in two transition state like manners, corresponding to the Exo and Endo transition state formations, and the systems optimised at the DFT/6-31G level. Vibrational analysis confirms that a transition state has been reached, in each case, with an imaginary negative vibrational frequency which corresponds to the maxima on the potential energy surface, the transition state.

LUMO+1 LUMO HOMO HOMO-1 Energy (Ha) Imaginary Vibration Animation Frequency of Vibration (cm-1) Jmol
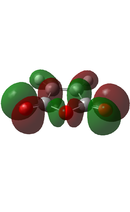
EXO[50]
Symmetric
Antisymmetric
Antisymmetric
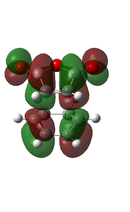
Symmetric		 -612.534265
-448.5050
ENDO[51]
Symmetric
Antisymmetric
Antisymmetric
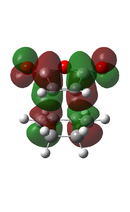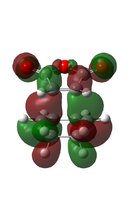Symmetric		 -612.538330
-446.8475
Figure 21: Summary of MOs and properties for the cyclohexadiene and maleic anhydride Diels-Alder transition states

The endo transition state was found to be lower in energy compared to the exo, as expected according to popular theory.

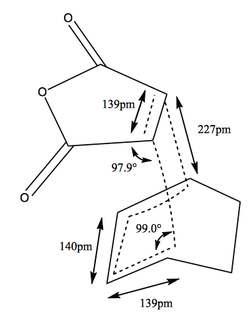
The structures of the transition states were compared, with the most interesting comparrison being the distance between the two fragments coming together in the transition state. The endo transition state and the typical butadiene-ethene transition state, are 227pm or 2.27 amstrong. Where as the exo transition state which is higher in energy compared to the endo, has the same distance as 2.29 amstrong, which confirms the less favourable interaction. These distance mentioned are much longer than an average C-C single bond still shorter than the sum of van der Waals radius of two carbons, which is 3.4Â. This makes sense for a transition state.

Another interesting comparrison is the angle of the forming bond in realtion to the cyclohexadiene. In the endo form this is 99.0°, however in the Exo it is 94.8°, this suggest that there is steric hindrance in the exo transition state between the maleic anhydride oxygens and the sp3 carbon atoms in the cyclohexadiene.

Ethene + Butadiene TS Geometry Cyclohexadiene and Maleic Anhydride Endo TS Geometry Cyclohexadiene and Maleic Anhydride Exo TS Geometry
6-31G
Figure 22: Comparison of Geometries of optimised(DFT/6-31G* level) Diels-Alder transition states

IRC analysis at B3LYP/6-31G(d)provides direct visualisation of the simultaneous formation of the two C-C bonds.

IRC Energy Graphs Animation Energy of Product (Ha)
EXO[52] 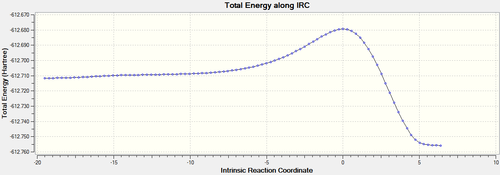-612.534265
ENDO[53] 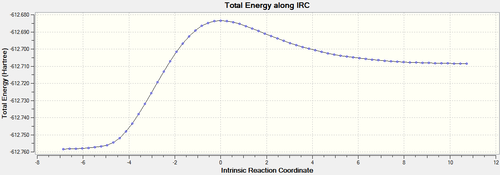-612.538330
Figure 23: Comparison of IRC's of cyclohexadiene and maleic anhydride Diels-Alder transition states


The endo TS is lower in energy, this can be explained by secondary orbital overlap,[54] while unfavorable steric interactions have been suggested as disfavoring the exo TS.[55] There is more steric hindrance in the exo transition state because the maleic anhydride oxygens are closer to the sp3 carbon atoms in the cyclohexadiene, as discussed earlier.

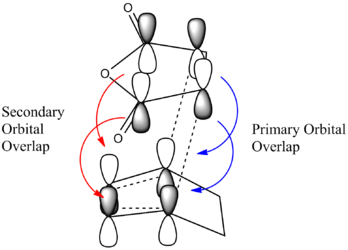
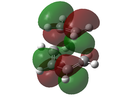
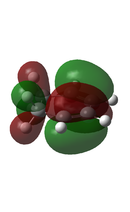
Figure 24: Stabalising endo secondary orbital interactions (LCAO)


There is eveidence of some secondary orbital interactions in some of the occupied molecular orbitals of the endo transition state. For example, there are favourable interactions between the carbonyl carbons and the diene (MOs 28 and 37) and between the anhydride oxygen and the diene (MO 43) which are absent in the exo transition state. There is also secondary orbital overlap in MO 50, however this is an unoccupied MO (HOMO = level 47), so this would be effectively zero.

It's possible the lower energy of the endo transition state is due to these secondary interactions.

MO Level 28 MO Level 37 MO Level 43 MO Level 50
Orbital Visualisation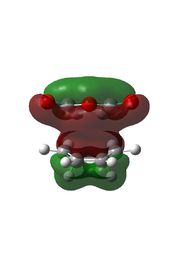
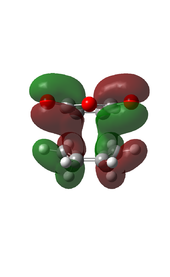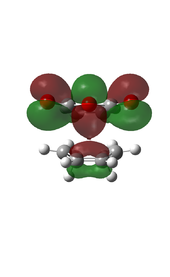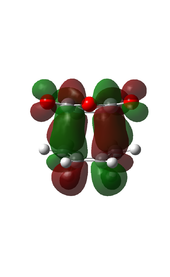Orbital Visualisation side
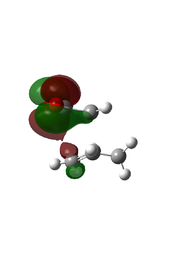Figure 25: Stabalising endo secondary orbital interactions (MO's)

Conclusions

The computational analysis of the Cope rearrangement, suggested that the most stable conformer of 1,5-hexadiene is the Anti-1 conformer. There is also evidence that the Chair transition state is lower in energy than the boat form and leads to the gauche 2 conformation. The Boat transition state has been seen to lead to the guache 3 conformation.

The Endo/ Exo prefernce rule has been confirmed with the Maleic anhydride and cyclohexadiene Diels-Alder reaction analysis. It is likely that steric and pauli repulsiosn are the origin of the endo preference in this particular case.

The computational methods used have proven to be not only accurate and reliable, beneficial to the study of transition states and conformational analysis. The methods are also useful due to the fact that transition states have very short lifetimes so conducting experimental measurements can be challenging. Computational chemistry is a field of chemistry that can only continue to grow and continue be useful in conjuction with experimental techniques in the future.


References

<references>

  1. ↑ Gaussian 09, Revision A.1, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
  2. ↑ The Development of Transition-State Theory, Kelth J. Laidler' and M. Chrlstlne Klng, J. Physical Chem. 1983, 87, 2657-2664
  3. ↑ A. C. Cope, E. M. Hardy, "The Introduction of Substituted Vinyl Groups. V. A Rearrangement Involving the Migration of an Allyl Group in a Three-Carbon System", Journal of the American Chemical Society, 1940,62, 441, DOI:10.1021/ja01859a055
  4. ↑ The Cope Rearrangement Revisited Again. Results of Ab Initio Calculations beyond the CASSCF Level, David A. Hrovat, Keiji Morokuma, and Weston Thatcher Borden, Journal of the American Chemical Society 1994 116 (3),
  5. ↑ Homoaromaticity, Richard Vaughan Williams, Chemical Reviews 2001 101 (5), 1185-1204
  6. ↑ Homoaromaticity, Richard Vaughan Williams, Chemical Reviews 2001 101 (5), 1185-1204
  7. ↑ H. Rzepa, Conformational Analysis lecture course 2011, page 'Alkanes', http://www.ch.ic.ac.uk/local/organic/conf/ Calculation: http://hdl.handle.net/10042/to-4857
  8. ↑ http://hdl.handle.net/10042/21237
  9. ↑ http://hdl.handle.net/10042/21242
  10. ↑ http://hdl.handle.net/10042/21238
  11. ↑ http://hdl.handle.net/10042/21239
  12. ↑ http://hdl.handle.net/10042/21240
  13. ↑ http://hdl.handle.net/10042/21241
  14. ↑ http://hdl.handle.net/10042/21233
  15. ↑ http://hdl.handle.net/10042/21234
  16. ↑ http://hdl.handle.net/10042/21235
  17. ↑ http://hdl.handle.net/10042/21236
  18. ↑ http://hdl.handle.net/10042/21246
  19. ↑ http://hdl.handle.net/10042/21244
  20. ↑ http://hdl.handle.net/10042/21401
  21. ↑ http://hdl.handle.net/10042/21247
  22. ↑ http://hdl.handle.net/10042/21245
  23. ↑ http://hdl.handle.net/10042/21248
  24. ↑ C. Banwell, Fundamentals of Molecular Spectroscopy, fourth ed. 1994, pg 86, Mcgraw-Hill, ISBN 0-07-707976-0
  25. ↑ http://hdl.handle.net/10042/21247
  26. ↑ http://hdl.handle.net/10042/21249
  27. ↑ http://hdl.handle.net/10042/21251
  28. ↑ http://hdl.handle.net/10042/21252
  29. ↑ http://hdl.handle.net/10042/21253
  30. ↑ http://hdl.handle.net/10042/21254
  31. ↑ http://hdl.handle.net/10042/21255
  32. ↑ http://hdl.handle.net/10042/21256
  33. ↑ http://hdl.handle.net/10042/21257
  34. ↑ http://hdl.handle.net/10042/21258
  35. ↑ 3rd Year Computational Chemistry Online Lab Manual, Module 3, 2011
  36. ↑ http://hdl.handle.net/10042/21537
  37. ↑ http://hdl.handle.net/10042/21251
  38. ↑ http://hdl.handle.net/10042/21246
  39. ↑ http://hdl.handle.net/10042/21402
  40. ↑ http://hdl.handle.net/10042/21254
  41. ↑ http://hdl.handle.net/10042/21404
  42. ↑ http://hdl.handle.net/10042/21520
  43. ↑ http://hdl.handle.net/10042/21519
  44. ↑ http://hdl.handle.net/10042/21521
  45. ↑ http://hdl.handle.net/10042/21512
  46. ↑ http://hdl.handle.net/10042/21511
  47. ↑ W. Carruthers, Cycloaddition Reactions in Organic Synthesis, pg 56, Pergamon Press 1990, ISBN 0-08-034712-6.
  48. ↑ http://hdl.handle.net/10042/21513
  49. ↑ http://hdl.handle.net/10042/21514
  50. ↑ http://hdl.handle.net/10042/21515
  51. ↑ http://hdl.handle.net/10042/21516
  52. ↑ http://hdl.handle.net/10042/21518
  53. ↑ http://hdl.handle.net/10042/21517
  54. ↑ Stereochemistry of Electrocyclic Reactions, R. B. Woodward and Roald Hoffmann, Journal of the American Chemical Society 1965 87 (2), 395-397
  55. ↑ Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies, Marye Anne Fox, Raul Cardona, and Nicoline J. Kiwiet, The Journal of Organic Chemistry 1987 52 (8), 1469-1474
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:abcmod3&oldid=818484"