Rep:Mod:abcmod2
Year 3 Computational Lab
Module 2: Bonding and molecular orbitals in main group compounds.
Alex Cook 00555113
Intro
Computational chemistry gives a useful insight into the structure and bonding for a variety of different applications. the commercial Gaussian software package will be used in this project for calculations and graphical output, which will enable analysis of orbitals and distribution of charge in molecules.[1] This is important for understanding of reactivity, structure and bonding, as already mentioned, but also allows understanding of transition states and thermodynamic information.
In this project various inorganic molecules will have their structures optimised in Gaussian via different methods and basis sets, and their energies compared. Also vibrational analysis will be carried out and the global energy minima verified. With natural bond orbital (NBO) calculations we will generate and analyse molecular orbitals and compare these to their Linear combination of atomic orbital (LCAO) equivalents.
The data gathered, graphical output, and analysis conducted would be very difficult to achieve in the lab, thus highlighting the importance of computational methods.
BH3
Here we will deal with the optimisation of geometry, vibrational analysis, molecular orbitals, and NBO analysis of the main group compound BH3.
Optimisation of geometry
3-21G basis set
The inital B-H bond lengths were set to 1.50 Å. Using Gausian the geometry of BH3 was optimised using the DFT/B3LYP method with the slightly basic basis set of 3-21G. This method is acceptable for BH3 because it is small and symmetric. This produced an optimised bond distance of 1.19 Å and a bond angle of 120.0°. the molecule was confirmed to be trigonal planar with a point group of D3h.
Log file here. summary below:
Filename = \\ic.ac.uk\homes\abc08\Desktop\3rdyearlab\module2\bh3optimisation.log BH3 optimisation File Name = bh3optimisation File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.46226338 a.u. RMS Gradient Norm = 0.00020672 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 4 minutes 12.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
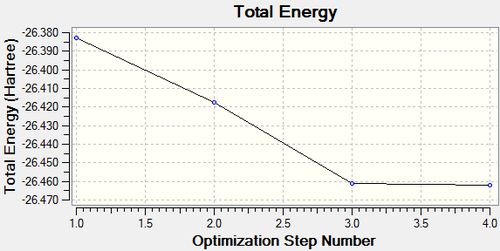
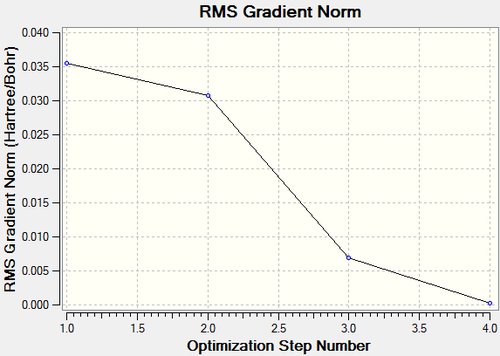
Figure 1 shows the total energy curve for the optimisation of BH3, it is a visualisation of the program traversing the potential energy surfaceof the molecule to locate the minimun energy structure, and it can be seen that by the third stucture the minimum energy optimised structure was found (fourth point). Figure 2 shows the RMS gradient moving towards zero as the calculation progresses and we move towards the minimum.[2]
6-31G(d,p) basis set
The structure obtained from the 3-21G basis set optimisation was then used to optimise the structure again this time using the higher level basis set 6-31G(d,p). this gave a D3h structure with B-H bond lengths of 1.19 Å, and bond angles of 120.0°. Log file here.
| Total energy of optimised BH3 / a.u. | ||
| 3-21G basis set | -26.46226338 | |
| 6-31G(d,p) basis set | -26.61532264 | |
The total energy for any computational chemistry calculation always depends on the basis set that was used. One can only compare energies with models that have the same number and type of atoms and when the same baisis-set (or pseudo potential) has been used on the each atom. [3] Thus a more relevant comparison is to compare the relative energies of different isomers of the same structure (more in mini-project).
Filename = \\ic.ac.uk\homes\abc08\Desktop\3rdyearlab\module2\BH3OPTIMISATION_631G_DP.log BH3 optimisation File Name = BH3OPTIMISATION_631G_DP File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -26.61532264 a.u. RMS Gradient Norm = 0.00021663 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = CS Job cpu time: 0 days 0 hours 4 minutes 17.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000434 0.000450 YES
RMS Force 0.000284 0.000300 YES
Maximum Displacement 0.001698 0.001800 YES
RMS Displacement 0.001114 0.001200 YES
Predicted change in Energy=-1.188111D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1914 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1914 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1914 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0001 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0001 -DE/DX = 0.0 !
! A3 A(3,1,4) 119.9999 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrational analysis
Using the 6-31G(d,p) optimised structure we will now carry out vibrational analysis to confirm we have minium structures. the results are below. Method: B3LYP, Basic Set: 6-31G(d,p). The Log file is here.
The first row of “low frequencies” correspond to the 3N-6 vibrational frequencies and should ideally be equal to zero. These are due to motion involving the centre of mass of the molecule, and can be reduced to +/- 10 cm-1 with use of a higher level method.
Filename = \\ic.ac.uk\homes\abc08\Desktop\3rdyearlab\module2\alexcook_bh3_freq.log BH3 frequency File Name = alexcook_bh3_freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -26.61532264 a.u. RMS Gradient Norm = 0.00021659 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = C2V Job cpu time: 0 days 0 hours 0 minutes 13.0 seconds.
Low frequencies --- -73.0837 -69.5094 -69.4394 -0.0009 -0.0007 0.0006
Low frequencies --- 1161.3810 1212.0964 1212.1646
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 1161.3810 1212.0964 1212.1646
Red. masses -- 1.2531 1.1072 1.1072
Frc consts -- 0.9958 0.9584 0.9585
IR Inten -- 92.7138 13.9832 13.9868
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.16 0.00 0.10 0.00 -0.10 0.00 0.00
2 1 0.00 0.00 -0.57 0.00 0.08 0.00 0.81 0.00 0.00
3 1 0.00 0.00 -0.57 -0.39 -0.59 0.00 0.14 0.39 0.00
4 1 0.00 0.00 -0.57 0.39 -0.59 0.00 0.14 -0.39 0.00
4 5 6
A A A
Frequencies -- 2587.8129 2721.5077 2721.5171
Red. masses -- 1.0078 1.1273 1.1273
Frc consts -- 3.9765 4.9196 4.9196
IR Inten -- 0.0000 126.1345 126.1315
Atom AN X Y Z X Y Z X Y Z
1 5 0.00 0.00 0.00 0.11 0.00 0.00 0.00 0.11 0.00
2 1 0.00 0.58 0.00 0.02 0.00 0.00 0.00 -0.81 0.00
3 1 0.50 -0.29 0.00 -0.60 0.36 0.00 0.36 -0.19 0.00
4 1 -0.50 -0.29 0.00 -0.60 -0.36 0.00 -0.36 -0.19 0.00
| Vibrational Mode | Symmetry Label | Absorption Intensity | Bond Frequency (cm-1) | Literature Value* (cm-1)[4] | Diagram |
|---|---|---|---|---|---|
| Umbrella deformation -
All Hydrogens move up and down in the plane at the same time. Strong intensity adsorption due to the large change in dipole moment. |
A2 " | 93 | 1161 | 1225 |  |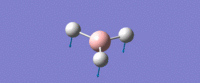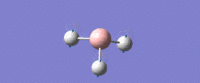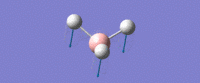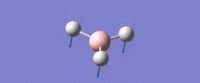
| Symmetric B-H scissoring -
Two Hydrogens move together and apart in a scisorring motin in the plane. the other H atom remain constant relative to the Boron. |
E' | 14 | 1212 | 1305 |  |
| Asymmetric B-H rocking -
Two of the H atoms are moving back and forth at the same time in a rocking motion in the plane of the molecule. The other H atom moves back and forth in the opposite direction still in the plane. |
E' | 14 | 1212 | 1305 |  |
| Symmetric B-H stretch -
All three Hydrogens move in and out at the same time, along their bonds and in the plane. |
A1' | 0 | 2588 | - |  |
| Asymmetric B-H stretch (1) -
Two Hydrogens move in and out in out in 'opposite phase' to each other, along their bonds in the plane of the molecule. The third H atom is stationary. The Boron mves slightly from side to side in time with the H atom coming in. |
E' | 126 | 2722 | 2693 |  |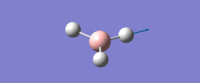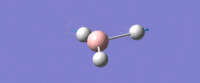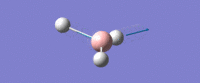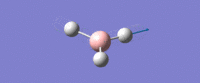
| Asymmetric B-H stretch (2) -
Two H atoms move in and out in a symmetric manner whilst the third moves in and out in 'opposite phase', all in the plane. The Boron moves slightly in time with the asymetric Hydrogen. |
E' | 126 | 2722 | 2813 |  |
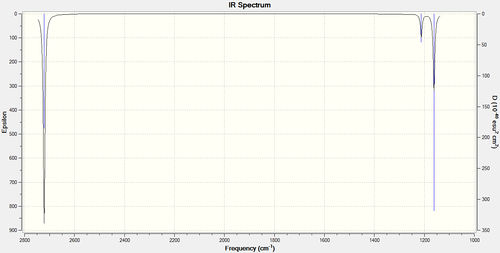
In theory there are 6 vibrational modes for BH3, however in the IR spectrum only 3 absorptions are seen. The A' B-H stretch has an intensity of 0 and no peak seen because there is no overall change in dipole moment due to it being a completely symmetric stretch. In addition there are two pairs of degenerate E' absorptions at 1212cm-1 and 2722cm-1, thus giving three adsorptions on the IR spectrum.
The literature values displayed are from another computational study of BH3, and are not experimental values.
Molecular orbital analysis
The 6-31G(d,p) basis set optimised BH3 structure was then used for molecular orbitla calculations using the High Performance Computer server, with the aditional keywords 'pop=full' and 'full nbo'. The results were then visualised in Gaussview, and a molecular orbital diagram produced in Chemdraw 13.0. The Log file is here.
| MO Diagram with Orbitals shown in the XY plane | Orbitals seen in XZ Plane | Molecular Orbital |
|---|---|---|
 | ||
 |
LUMO+3 | |
 |
LUMO+2 | |
 |
LUMO+1 | |
 |
LUMO | |
 |
HOMO | |
 |
HOMO-1 | |
 |
HOMO-2 | |
 |
HOMO-3 |
The energy levels were determined in accordance with the relative splitting energy. the splitting energy is the difference in energy between the MOs and the component fragment orbitals. The splitting energies shown in figure x are only a qualitative approximation; a definative orbital approxitmation could be obtain with further calculations.
The diagram was estimated considering H is more electronegative than boron, and thus the H3 fragment is lower than their boron counterpart. An interesting feature is that the LUMO is negative in energy, meaning that it can accept a pair of electrons without becoming destabalised, which is consistent with the fact that it is lewis acidic.
The real MOs and their respective LCAO apprpximations match well. The computational method is a simple method to achieve an accurate calculation of the Molecular orbitals involved in molecules, and would be even more useful in higher complexity molecules. But equally the LCAO method shows good agreement and is a fast way to understand the molecular orbitals of more simple molecules without the need for computational analysis.
BBr3
Optimisation
This compound involves heavy Bromine atoms which need to be treated with a pseudo-potential, but also Boron which needs to be treated as a light atom and thus a full basis set needs to be used.[5] So this example is conducted by mixing psueod-potentials and basis sets, acheived by directly adjusting the input Gaussian input file in text with the following lines:
B Br 0 6-31G(d,p) **** Br 0 LanL2DZ **** Br 0 LanL2DZ
This gave a BBr3 structure with B-Br bond lengths of 1.92 Å, and bond angles of 120.0°. The Log file is here.
Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/module2/BBR3OPTIMISATION_GEN.LOG BBr3 optimisation File Name = BBR3OPTIMISATION_GEN File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -64.46515476 a.u. RMS Gradient Norm = 0.01646826 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C2V Job cpu time: 0 days 0 hours 2 minutes 31.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000011 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.000054 0.001800 YES
RMS Displacement 0.000032 0.001200 YES
Predicted change in Energy=-7.659615D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.9232 -DE/DX = 0.0 !
! R2 R(1,3) 1.9232 -DE/DX = 0.0 !
! R3 R(1,4) 1.9232 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0037 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0037 -DE/DX = 0.0 !
! A3 A(3,1,4) 119.9926 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
TlBr3
Optimisation
The optimisation was carried out under the method B3LYP and the basis set LANL2DZ. This basis set is medium level, and uses D95V on first row elements but uses pseudo potentials (Los Alamos ECP) on heavier atoms.[6]
In this example the point group symmetry was constrained to D3h with a very tight tollerance.
The Log file is here.
Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/module2/log_63059.out TlBr3optimisation File Name = log_63059 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 a.u. RMS Gradient Norm = 0.00000090 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 19.6 seconds.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.083024D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrational analysis
A frequency analysis was carried out, this is important as it cacn confirm that an optimised structure has been found.
Log file is here.
| Vibrationa mode | Symmetry label | Absorption Intensity | Absorption frequency (cm-1) | Diagram |
|---|---|---|---|---|
| Symmetric Tl-Br scissoring -
Two Bromine move together and apart in a scissoring motion in the plane. The other Br atom remain constant relative to the Thalium. |
E' | 4 | 50 |  |
| Asymmetric Tl-Br rocking -
Two of the Br atoms are moving back and forth at the same time in a rocking motion in the plane of the molecule. The other Br atom moves back and forth in the opposite direction still in the plane. |
E' | 4 | 50 |  |
| Umbrella deformation -
All Bromine atoms move up and down in the plane at the same time. Strong intensity adsorption due to the large change in dipole moment. |
A2 " | 6 | 57 |  |
| Symmetric Tl-Br stretch -
All three Hydrogens move in and out at the same time, along their bonds and in the plane. |
A1' | 0 | 151 |  |
| Asymmetric Tl-Br stretch -
Two Bromine atoms move in and out in out in 'opposite phase' to each other, along their bonds in the plane of the molecule. The third Br atom is stationary. The Thalium mves slightly from side to side in time with the Br atom coming in. |
E' | 24 | 195 |  |
| Asymmetric Tl-Br stretch -
Two Tl-Br bonds stretch symmetrically with eachother and the other Tl-Br bond stretches asymmetrically with respect to the other two. |
E' | 24 | 195 |  |
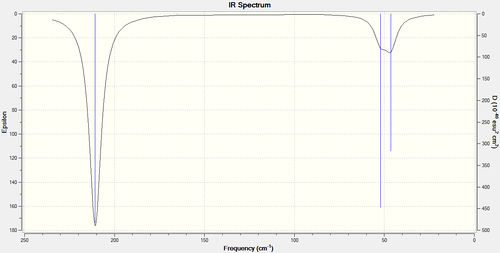
Tl-Br is a weaker bond than B-H thus has lower frequnecy modes. There has been a reordering of the modes. In BH3 the lowest mode is A2', whilst in TlBr3 the two E' degenerate modes have the lowest frequency and are the lowest 'real modes'. The closer to zero the low frequencies are, the more reliable and accurate the results. The IR spectrum shows three peaks which is in agreement with the literature.[7]
Trigonal planar comparrison
Changing the ligand from Hydrogen to Bromine causes a lengthening of the B-Ligand bond. The group 13 atom boron contributes one electron to each of the three bonds, bromine also contributes one electron each, but is left with 3 lone pairs after bonding. Bromine is a much larger atom with more diffuse electron cloud, resulting in a poor orbital overlap and weak, hench longer bond. the hydrogens s orbitals on the other hand has a much more effective overlap and thus greater bonding interaction.
On changing of the central atom, ie. changing from form BBr3 to TlBr3, the bonds lengthen also. Thallium and boron are both in group 13, but using a similar argument to above, the thallium is a larger atom with more difuse orbitals leading to a less effective orbital overlap and longer weaker Tl-Br bond.
| BH3 | BBr3 | TlBr3 | |
|---|---|---|---|
| Bond length (Å) | 1.19 | 1.92 | 2.65 |
| Lit. Bond Length (Å) | 1.187[8] | 1.90[9] | 2.512[10] |
Gausvieww has a set of bond lengths that it associates with molectues based on the distance between the two atoms. ocassionally gaussian cant find a bond length to fit the distances so it doesnt draw a bond. In reality however there could very well be a bonding interaction. this more often happens with inorganic complexes, as they generally have longer bonds.
In computational chemistry we require a strict set of parameters to define a bond. It is sometimes difficult to define a bond like this though be cause there are many variances in bonds. there are ionic bonds which are an electrostatic attraction between two atoms. A covalent bond occurs with the overlap of molecular orbitals in neighbouring atoms. Most of the time bonds are a mixture of the two, meaning every bond is different, and difficult to apply strict parameters to.
NH3
Optimisation
A molecule of Ammonia was optimised using the method B3LYP and basis set 6-31G(d,p). The log file is here.
Filename = \\ic.ac.uk\homes\abc08\Desktop\3rdyearlab\module2\nh3\alexcook_nh3_631g_dp.log alexcook_nh3_631g_dp File Name = alexcook_nh3_631g_dp File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -56.55776856 a.u. RMS Gradient Norm = 0.00000885 a.u. Imaginary Freq = Dipole Moment = 1.8464 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 32.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000079 0.001800 YES
RMS Displacement 0.000053 0.001200 YES
Predicted change in Energy=-1.629729D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7413 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7486 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7479 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 111.8631 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrational analysis
Vibrational analysis was carried out on the opimised molecule. The log file is here.
Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/module2/nh3/freq/ALEXCOOK_NH3_FREQ.LOG alexcook_nh3_freq File Name = ALEXCOOK_NH3_FREQ File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -56.55704661 a.u. RMS Gradient Norm = 0.00831778 a.u. Imaginary Freq = 0 Dipole Moment = 1.7558 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 15.0 seconds.
Low frequencies --- -445.1990 -443.5098 -422.9147 -0.0013 -0.0005 0.0010
Low frequencies --- 911.7038 1661.1661 1661.4246
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 911.7032 1661.1130 1661.3736
Red. masses -- 1.1826 1.0674 1.0674
Frc consts -- 0.5791 1.7354 1.7359
IR Inten -- 183.2026 16.8347 16.8275
Atom AN X Y Z X Y Z X Y Z
1 7 0.12 0.00 0.00 0.00 -0.03 -0.06 0.00 0.06 -0.03
2 1 -0.54 -0.20 0.00 -0.11 -0.06 0.69 0.22 0.12 0.33
3 1 -0.54 0.10 -0.17 -0.14 0.59 0.25 -0.20 -0.32 -0.31
4 1 -0.54 0.10 0.17 0.24 -0.12 -0.09 -0.02 -0.66 0.39
4 5 6
A A A
Frequencies -- 3654.8458 3800.1013 3800.6261
Red. masses -- 1.0253 1.0907 1.0907
Frc consts -- 8.0691 9.2797 9.2825
IR Inten -- 0.1793 0.2310 0.2353
Atom AN X Y Z X Y Z X Y Z
1 7 0.04 0.00 0.00 0.00 0.04 0.07 0.00 0.07 -0.04
2 1 -0.17 0.55 0.00 0.15 -0.39 0.02 0.25 -0.65 -0.01
3 1 -0.17 -0.28 0.48 0.14 0.20 -0.31 -0.25 -0.32 0.58
4 1 -0.17 -0.28 -0.48 -0.29 -0.38 -0.66 0.00 0.02 0.00
Molecular orbital analysis
Molecular Orbital analysis was carried out. Log file is here.
| MO Diagram with Orbitals shown in the XY plane | Orbitals seen in YZ Plane | Molecular Orbital |
|---|---|---|
 | ||
 |
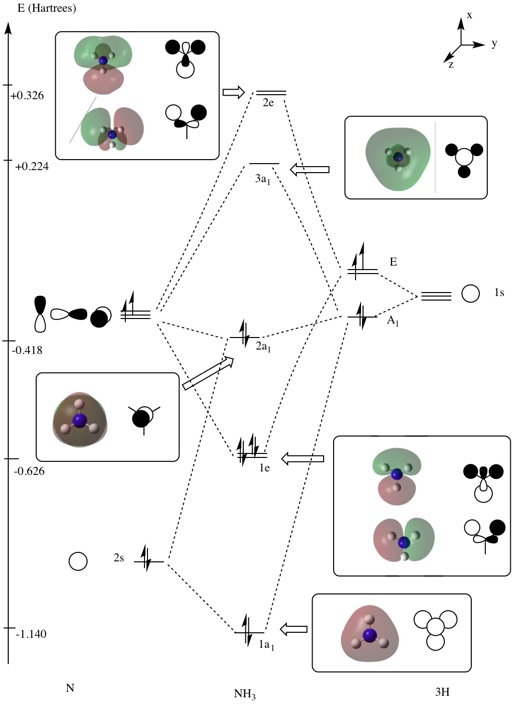LUMO+2 | |
 |
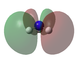LUMO+1 | |
 |
LUMO | |
 |
HOMO | |
 |
HOMO-1 | |
 |
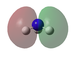HOMO-2 | |
 |
HOMO-3 |
NBO Analysis
The charge distribution shows that the Nitrogen atom is red and negatively charged. This is due to the lone pair of electrons present in the Nitrogen p-orbital and the high electronegativity of Nitrogen.
| Charge distribution colour key | NBO Charge distribution colour diagram | NBO Charge distribution |
 |
 |
 |
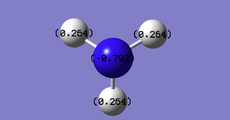NH3BH3 Dissociation
A molecule of Ammonia-Borane was optimised in Gaussian at the b3lyp/631-G(d,p) level. The Gaussian log file for the optimisation can be found here. The calculation converged to a staitionary point as seen here:
Item Value Threshold Converged?
Maximum Force 0.000121 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000508 0.001800 YES
RMS Displacement 0.000294 0.001200 YES
Predicted change in Energy=-1.611643D-07
Optimization completed.
-- Stationary point found.
A frequency analysis was carried out to ensure a minimum was found. The Gaussian log file for the optimisation can be found here.
Low frequencies --- 0.0005 0.0012 0.0015 18.5329 23.7785 41.0366 Low frequencies --- 266.2888 632.2326 639.8278
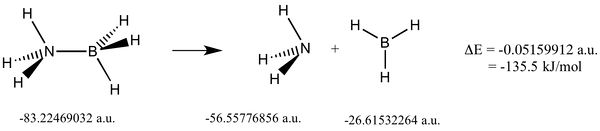
Lit. value for bond = 130kJ/mol.[11] The negative change in energy indicates that relative to the dimer the two seperate moleculers of Ammonia and Borane is a more stable configuration.
Mini-Project - Bonding in Main Group Halides
AlCl3 is a trigonal planar structure, however it likes to form a dimer with two bridging Chlorines forming three centre - two electron bonds, and 4 terminal Chlorines. The aim of this project is to investigate possible structures and stabilities of the dimer when 2 chlorines are substituted for bromines. this will be done by using methods from the previous section, icluding analysis of the relative optimised energies of the different conformational isomers, frequency analysis and studying the Molecular Orbitals of the possible structures.
Most structures of this class are Lewis acidic at the Aluminium centres (or Boron in the case of B2H6 etc) and easily accept a lone pair of electrons to form thier respective dimers. Reactions of the dimer with a base will readily cleave the molecule either homolytically or heterolytically, depending on the nature of the base used.[12]
Optimisations
The structures were drawn and their geometries were optimised using a full basis set 6-31G(d,p) on Aluminium and Chlorine, and a LANL2DZ pseudo potential on the Bromines. This was set up by altering the input file directly (using similar code to the previous section when mixing basis sets and pseudo potentials). THis was done with the following code:
Al Cl 0 6-31G(d,p) **** Br 0 LanL2DZ **** Br 0 LanL2DZ
Summaries for the optimisationsa are below:
Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/module2 part2/isomer1/isomer1i.out 631g(dp)_isomer1 File Name = isomer1i File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -2352.41633415 a.u. RMS Gradient Norm = 0.00001539 a.u. Imaginary Freq = Dipole Moment = 0.1898 Debye Point Group = C1 Job cpu time: 0 days 0 hours 3 minutes 30.7 seconds.
Filename = \\ic.ac.uk\homes\abc08\Desktop\3rdyearlab\module2 part2\isomer2\New folder\NEWisomer2.log NEWisomer2 File Name = NEWisomer2 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -2352.40631946 a.u. RMS Gradient Norm = 0.00001186 a.u. Imaginary Freq = Dipole Moment = 0.0008 Debye Point Group = C1 Job cpu time: 0 days 0 hours 7 minutes 23.0 seconds.
Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/module2 part2/isomer3/isomer3i.out 631g(dp)_isomer3 File Name = isomer3i File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -2352.41628782 a.u. RMS Gradient Norm = 0.00001617 a.u. Imaginary Freq = Dipole Moment = 0.1786 Debye Point Group = C1 Job cpu time: 0 days 0 hours 4 minutes 4.5 seconds.
Filename = //ic.ac.uk/homes/abc08/Desktop/3rdyearlab/module2 part2/isomer4/New folder/NEWISOMER4.LOG NEWisomer4 File Name = NEWISOMER4 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -2352.41630699 a.u. RMS Gradient Norm = 0.00003095 a.u. Imaginary Freq = Dipole Moment = 0.0045 Debye Point Group = C1 Job cpu time: 0 days 0 hours 5 minutes 16.0 seconds.
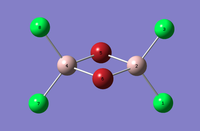
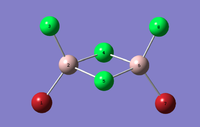
| Dimer | Al2Cl4Br2 (geminal) | Al2Cl4Br2 (bridging) | Al2Cl4Br2 (cis) | Al2Cl4Br2 (trans) |
|---|---|---|---|---|
| 3D Optimised structure |  |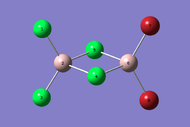
 |
 |
|
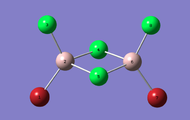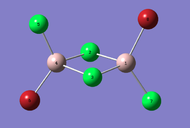
| Symmetry | C2v | D2h | C2v | C2h |
| Energy / a.u. | -2352.41633415 | -2352.40631946 | -2352.41628782 | -2352.41630699 |
| Energy / kJmol-1 | -6176267.601905 | -6176241.308343 | -6176267.480265 | -6176267.530596 |
| Difference in Energy relative to lowest Energy Dimer / kJmol-1 | 0.000 | 26.294 | 0.122 | 0.071 |
| Terminal Al-Cl Bond Length (Å) | 2.09 | 2.09 | 2.09 | 2.09 |
| Bridging Al-Cl Bond Length (Å) | 2.30 | - | 2.30 | 2.30 |
| Terminal Al-Br Bond Length (Å) | 2.28 | - | 2.28 | 2.28 |
| Bridging Al-Br Bond Length (Å) | - | 2.49 | - | - |
| Terminal Bond angle (°) | 121.7 (Cl-Al-Cl), 121.5 (Br-Al-Br) | 121.6 | 121.5 | 121.5 |
| Bridge Bond angle (°) | 89.9 | 88.3 | 89.8 | 89.9 |
| DOI for calculation | Isomer 1 geminal | Isomer 2 bridging | Isomer 3 cis | Isomer 4 trans |
When we look at the energies of the structure it can be seen the the geminal isomer has the lowest total energy and is thus the most stable, with the bridging isomer being the least stable. The briding isomer has the large bromine atoms in bridging position under steric strain, causing the molecule to be less stable. This is steric strain is confirmed when we see that the bridging angle for Al-Br-Al is 88.3 compared to the less strained Al-Cl-Al bridging angle of 89.9 for the geminal, cis and trans isomers.
The Al-Cl bridging bonds are longer than the Al-Cl terminal bonds. this relationship is also true for the Al-Br bonds too. the bridging bonds involve 4 electrons and 3 centres, thus the electron cloud is more spread out and diffuse than for the terminal 2 electron 2 centre bonds. so the bridging bonds are longer and weaker. a comparison of the terminal Chlorine bonds to the terminal Bromine bonds shows that the Al-Cl bonds are shorter because of less diffuse Cl orbitals allowing for a better overlap and stronger bond.
Al2Cl2Br4 Dissociation
Reactions of the dimer with a base will readily cleave the molecule either homolytically or heterolytically, depending on the nature of the base used.[13] The structures of the fragments were drawn and their geometries were optimised using a full basis set 6-31G(d,p) on Aluminium and Chlorine, and a LANL2DZ pseudo potential on the Bromine's. The Log files for fragments are here: AlCl2Br, AlCl3, AlClBr2.
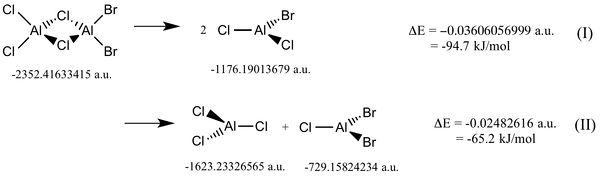
When the dimer dissociates into two dimers, the change in energy is negative, and about the magnitude of a bond enthalpy, as expected. It is interesting to note that homolytic cleavage produces an overall more negative change in energy. Although it is not so much a bond cleavage as it involves rearrangement of the Bromine atoms.
Vibrational Analysis
Vibrational analysis was carried out. The low frequencies are below:
Isomer 1 geminal
Low frequencies --- -26.1476 -24.8625 -14.0107 0.0008 0.0010 0.0015 Low frequencies --- 11.7996 51.4566 67.2938
Isomer 2 bridging
Low frequencies --- -25.7487 -24.5050 -14.1141 -0.0047 -0.0040 -0.0030 Low frequencies --- 13.9095 51.4493 67.2876
Isomer 3 cis
Low frequencies --- -25.6159 -21.0402 -19.5577 -13.7500 -0.0017 -0.0008 Low frequencies --- 0.0009 47.3233 77.8191
Isomer 4 trans
Low frequencies --- -25.3351 -21.3100 -19.5784 -14.0735 -0.0008 0.0037 Low frequencies --- 0.0037 47.3595 77.8002
| Structures | |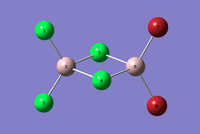
|
|
|
|---|---|---|---|---|
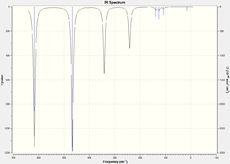
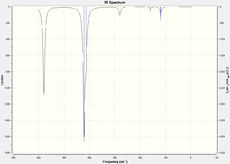
| IR spectra |  |
 |
 |
|
| Vibrational Mode | Geminal Isomer Vibrational Frequency, cm-1 [Intensity] | Bridging Isomer Vibrational Frequency, cm-1 [Intensity] | Cis Isomer Vibrational Frequency, cm-1 [Intensity] | Trans Isomer Vibrational Frequency, cm-1 [Intensity] |
|---|---|---|---|---|
| 1 -
The Aluminium atoms move back and forth at the same time, in the plane of the briding atoms.Y-axis movement of Aluminium atoms. |
412 [150] | 341 [161] | 412 [150] | 413 [149] |
| 2 -
The Aluminium atoms move left and right at the same time, in the plane of the briding atoms. Z-axis movement of Aluminium atoms. |
421 [299] | 467 [346] | 437 [416] | 421 [438] |
| 3 -
The Aluminium atoms move up and down at the same time. X-axis movement of Aluminium atoms. |
611 [188] | 617 [332] | 592 [310] | 579 [316] |
| File | Isomer 1 geminal | Isomer 2 bridging | Isomer 3 cis | Isomer 4 trans |
The vibration modes are the same for all the conformational isomers, however there are difference in the spectra due to the different positionings of the Br atoms, this affects the symmetry, which in turn affects the complexity of the spectra. the Br atom positioning also affects the respective dipole moments causing some peaks to not be active.
The spectra for the geminal isomer has more peaks due to it being the least symmetric isomer. the bridging isomer on the other hand is the most symmetric and has fewer, and alot more ordered and evenly spaced peaks.
In order for a Vibration to be IR active there must be a change in dipole moment. The trans isomer has very low intensities for some peaks due to the vibrational modes not causing a large change in dipole moment.
When the Br atoms are in the bridging position then vibrational mode 1 involves large vibrations of the Al-Br bonds. The Al-Br bonds are weaker than the Al-Cl bonds, thus the mode 1 peak for the trans isomer (341 cm-1) is at a significantly lower frequency than for the three other isomers (412 cm-1).
For Al2Cl4Br2, according to the literature there are Al-Cl and Al-Br stretches at 595 cm-1, 506 cm-1, for a sample in HCL at 80K.[14]
MO Analysis
Molecular orbitals were calculated and visualised for the most stable geminal isomer.
The molecular orbitals 35, 51, 52 below all display strong bonding character between the two geminal bromine atoms, which are well matched in orbital size. these bonding interactions would be lost in a different conformer, where the Bromines arent close to each other and no orbital overlap could be achieved. this agrees with the earlier conclusion that the geminal isomer would be the most stable.
the chlorine atoms have much smaller atomic orbitals and less diffuse orbitals, leading to not as good bonding overlap. the chlorine atomic orbitals are smaller due to the nucleus being very electrnegative, drawing the electrons in tight.
the antibonding molecular orbital 60 is included for a visual example of an antibonding orbital. there are alot of antibonding nodes making it a not very energetically favoured orbital.
the HOMO (54) and LUMO (55) are also inluded. there appears to be bonding overlap between the bridging chlorine atomic orbitals and the outer aluminium atomic orbitals. the LUMO has a negative energy , meaning electrons can be added without destabalising the molecule.
| Molecular Orbital Number | Image Of Molecular Orbital | mo levels |
|---|---|---|
| 60 |  |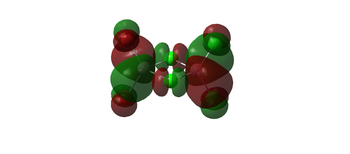
|
| 55 |  | |
| 54 |  | |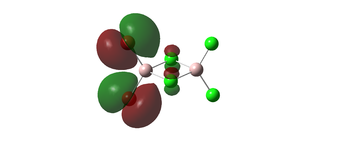
| 52 |  | |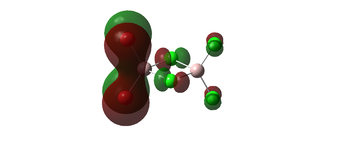
| 51 |  | |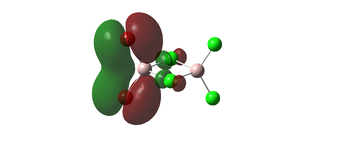
| 35 |  |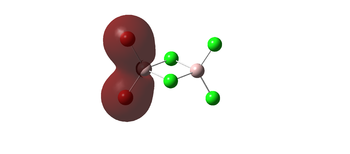
Conclusion
Computational techniques have proven to be very usefull. It provides good data for the investigation of stability of molecules, their theoretical physical attributes, and the affect of heavy atom substitution. the data collected in this report showed good agreement with the literature.
the structure optimisation methods used allowed us to identify isomers and their relative stabilities. Aluminium trihalide dimers are quite reactive so would be hard to observe their IR data in practice, so the gaussian vibrational analysis is useful. the vibration analysis can also show us that the optimisation has reached a minimum energy. Analysis of the molecular orbitals and NBOs showed us where the majority of the electron density was located and the bonding interactions associated.
The value of computational analysis is evident, its enables us to better understand bonding, structure, and reactivity.
References
- ↑ Atkins Physical Chem 7th ed. page 444
- ↑ Hunt, P., Year 3 Computational Lab script 2012, 'Understanding Optimisations part B' http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/3b_understand_opt.html
- ↑ Hunt, P., Year 3 Computational Lab script 2012, 'Using a Better Basis Set' http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/4b_better_basis.html
- ↑ K. Kawaguchi, J. E. Butler, C. Yamada, S. H. Bauer, T. Minowa, H. Kanamori, E. Hirota, J. Chem. Phys., 1987, 87, 2438. DOI:10.1063/1.453135
- ↑ Hunt, P., Year 3 Computational Lab script 2012, 'Using a mixture of basis sets and pseudo potentials' http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/4c_mixed_pp_basis.html
- ↑ Hunt, P., Year 3 Computational Lab script 2012,'Using pseudo potentials and larger basis sets' http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/4b_creating_bcl3.html
- ↑ J. Blixt, J. Glaser, J. Mink, I. Persson, P. Persson, M. Sandstroem. J. Am. Chem. Soc., 1995, 117 (18), pp 5089–5104 DOI:10.1021/ja00123a011
- ↑ Schuurman MS, Allen WD, Schaefer HF 3rd, 'The ab initio limit quartic force field of BH3' J Comput Chem. 2005 Aug;26(11):1106-12.
- ↑ G. Santiso-Quin ̃ones and I. Krossing, 'Reference Values for the B-X Bond Lengths of BI3 and BBr3 DOI:http://dx.doi.org/10.1002/zaac.200700510
- ↑ Glaser J., Johansson G., 'On the Structures of the Hydrated Thallium(III) Ion and its Bromide Complexes in Aqueous Solution', Acta Chemica Scandinavica A 36 (1982) 125-135.
- ↑ S. Xie, Y. Song, and Z. Liu, Can. J. Chem. 87, 1235–1247 (2009).
- ↑ P.Lickiss, 2nd Year Inorganic Chemistry Course, I2 - Main Group Chemistry, 2011, Lectures 5 and 6
- ↑ P.Lickiss, 2nd Year Inorganic Chemistry Course, I2 - Main Group Chemistry, 2011, Lectures 5 and 6
- ↑ M.I. Shilina, T.N. Rostovshchikova, O.V. Zagorskaya, V.V. Smirnov, Application of low temperature IR spectroscopy for studies of catalyst properties and dynamics on the example of aluminum halide complexes, Journal of Molecular Catalysis A: Chemical, Volume 146, Issues 1–2, 20 October 1999, Pages 335-341, ISSN 1381-1169, 10.1016/S1381-1169(99)00278-2.