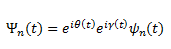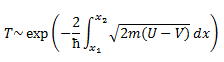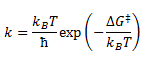Rep:Mod:aal109 phys
Module 3: Transition State and Reactivity
Transition state theory is is a microscopic theory that aims to rationalise rates of chemical reaction in terms of the potential energy surface. A transition state is defined as the structure corresponding to a saddle point on the potential energy (hyper)surface. [1] The theory is predicated on 4 main assumptions.
Firstly, the Born-Oppenheimer approximation is used, where nuclear and electronic degrees of freedom are separated and enables the construction of a potential energy (hyper)surface as a function of atomic coordinates. In the Born Oppenheimer formalism, the perturbation due to nuclear motion is slow, and thus the motion of the electron can be assumed to respond adiabatically, and the adiabatic theorem can be invoked, which states that under slow perturbation, a particle that is in the n eigenstate of the unperturbed Hamiltonian (ψn) will remain at the n eigenstate under pertubation (Ψn) except picking up two imaginary phase factors (the dynamic phase θ(t) and geometric phase γ(t)).
The Born-Oppenheimer approximation need not to hold true, and chemical reactions may involve multiple potential energy surfaces corresponding to multiple electronic states. Very strong diabatic coupling between electronic states are manifested in the cases of conical intersection, when the potential energy surface associated with the electronic states intersect at some point. [2] Those interactions are forbidden by the "non-crossing rule", which holds in the Born-Oppenheimer regime and forbids the crossing of electronic state belonging to the same symmetry. Conical intersections creates a funnel in the potential energy surface that enables radiationless crossing from excited to ground state and are important for understanding photochemical reactions such as photochemically driven pericylic reactions. [3]. Strong diabatic effects are also seen in systems susceptible to the Jahn-Teller effect, where small perturbation of nuclear position causes breaking of symmetry of the molecule and destroys the degeneracy of electronic states. This allows mixing of molecular orbitals that are forbidden before the reduction in molecular symmetry and dramatically changes the energy of the system.
Secondly, the transition state assumes that reactants are in equilibrium with the transition state. This is true only in the presence of strong coupling between the environment and the reacting system so as to allow rapid supply and dissipation of energy. If the reacting system is not strongly coupled to the environment, the rate of reaction is limited by the flow of energy from the surrounding to the reacting system akin to uni-molecular kinetics observed in the low pressure regime of Lindemann-Hinselwood kinetics. In such circumstances, the transition state is not in equilibrium with the reactants, and transition state theory breaks down. [4]
Thirdly, transition state theory assumes that the transition state cannot be re-crossed. Once the activation barrier is crossed, the reaction is irreversible. Transition state recrossing can be brought about by, for example, solvent cage effect, where the system is effectively reflected by the solvent-imposed barrier on the product side of the potential energy surface. [5] The system may also recross the transition state when the energy is not effectively dissipated by the environment and too much excess energy remains in the reaction coordinate after reaction for too long a time. [6] Conversely,reactions need not pass through the transition state. Quantum tunneling allows the system to tunnel through energy barriers that are above the energy of the system. Tunneling is more prevalent in light atoms, and this can be seen by the form of the Gamow tunneling formula obtained using semicalssical WKB approximation, which expresses the expressing the transmission coefficient T in terms of mass of the particle, depth of the energy well V and total energy of the particle U.
Transition theory is completely futile when dynamic effects are important, where 1 transition state could lead to multiple products. i.e. the product channel is bifurcated and the energy of the transition state has no influence on product distribution. In that case, the energy of the transition state has no bearing on the distribution of product. Rather, the position of the transition state with respect to various products on the potential energy hypersurface, and the topology of the potential energy surface, determines the product distribution. [7] Product distribution in such reaction depends on which products are easier to reach on the potential energy surface by the dynamic trajectory of the system, rather than simple thermodynamic or kinetic control arguments. Dynamic product channel bifurcation are found to be important in simple reactions such as rearrangement, elimination, addition, and substitution. [7] A related pitfall in transition state theory is complete avoidance of minimum energy pathway by the reactants if the system has a large internal energy. For example, theoretical calculations showed that the ion-paired intermediate in the exit channel of the minimum energy pathway of SN2 reaction can be completely avoided by the trajectory of the system. [8]
Despite all the shortcomings, the transition state has been observed experimentally using Femotosecond spectroscopy. The celebrated femosecond transient absorption experiment on photodissociation of NaI [9] has allow buildup and decay of the transition state to be captured using spectroscopy. Theoretically, the transition state is characterized 1 imaginary vibration frequency corresponding to the vibration in the direction of the reaction coordinate. Thus the structure and energy of transition states can be studied using computation methods.
If the assumptions of transition state theory is fulfilled, the rate of the reaction can be calculated using the Eyring equation
where ΔGΤ is the Gibbs Free Energy of activation and is the free energy difference between reactant and transition state.
The Cope Rearrangement
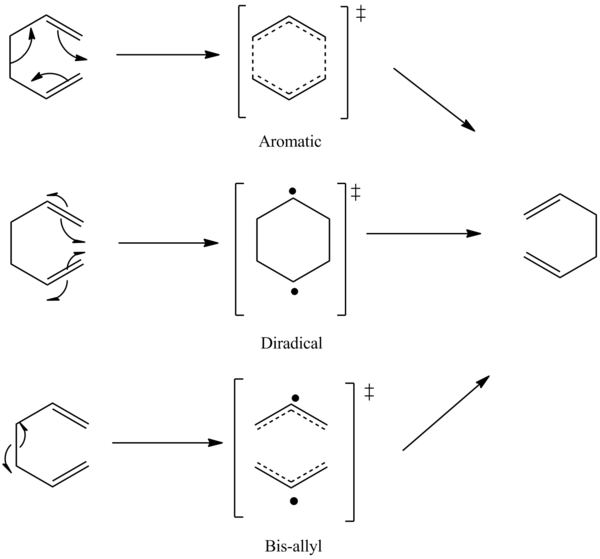
The Cope rearrangement is a [3,3] sigmatropic rearrangement of 1,5-dienes discovered by A. Cope in 1940. [10] The mechanism of Cope Rearrangement is subjected to controversy in the last 3 decades. The bis-allyl transition state, 1,4-diyl and aromatic transition state which is inbetween the two extremes have been suggested in the literature. [11]
The three transition states can be differentiated by the inter-allyl distance, and it is found that the potential energy hypersurface as a function of inter-allyl separation is very flat, suggesting a somewhat continuum between the biradical or bis-allyl extreme. It is found that there is a large substituent effect on the nature of the transition state. Doering and Wang [12] coined a "chameleonic" and and "centauric" transition state, which differ from substituent electronic effect at the 2,5 (nodal) and 1,3,4,6 (active) positions.
.
In the "chameleoic" model, radical stabilizing substituents at the active positions shifts the transition state towards two non-interacting allyl radicals, whereas radical stabilisng substituents at the nodal positions shifts the transition state towards the 1,4 diradical extreme. The chemeleoic model applies when the substituent effects works cooperatively. On the other hand, in the case of competitive or conflicting substituent effects, the "centauric" model applies, where a transition is envisaged between a partially 1,4 diradical, partially bisallyl hybrid, where half of the transition state behaves as if a allyl fragment and the other half behaves as a localised radical. [13]
In order to locate the transition state of the reaction, the degenerate Cope Rearrangement between 1,5-hexadiene is located.
Optimising the Reactant and Product
The reactant (which is structurally identical to the product) is optimised using HF/3-21g method. In this relatively flexible system, both anti and gauche conformation is possible, and the vinyl group can be orientated parallel or anti-parallel. In order to access the relative energy of anti and gauche conformation, and how relative orientation of the vinyl group affects the energy of the system, the C2-C1-C6-C5 dihedral angle is scanned to find low energy conformers.
| Dihedral Angle | Energy/Hatree |
|---|---|
| |
| 180 | -231.6925645 |
| 190 | -231.6919477 |
| 200 | -231.6907167 |
| 210 | -231.6891715 |
| 220 | -231.6876989 |
| 230 | -231.68669 |
| 240 | -231.6864362 |
| 250 | -231.687021 |
| 260 | -231.6882616 |
| 270 | -231.6897225 |
| 280 | -231.690899 |
| 290 | -231.6915565 |
| 300 | -231.6916076 |
| 310 | -231.6909716 |
| 320 | -231.6897099 |
| 330 | -231.6880904 |
| 340 | -231.6865227 |
| 350 | -231.6854163 |
| 360 | -231.6850465 |
| 10 | -231.6854817 |
| 20 | -231.686591 |
| 30 | -231.6880975 |
| 40 | -231.6896427 |
| 50 | -231.6908625 |
| 60 | -231.6914817 |
| 70 | -231.6913862 |
| 80 | -231.6906195 |
| 90 | -231.6893764 |
| 100 | -231.6880415 |
| 110 | -231.6870809 |
| 120 | -231.686838 |
| 130 | -231.687411 |
| 140 | -231.6886347 |
| 150 | -231.6901517 |
| 160 | -231.6915354 |
| 170 | -231.692415 |
| 180 | -231.6925645 |
| Dihedral Angle | Energy/Hatree |
|---|---|
| |
| 180 | -231.6925353 |
| 190 | -231.6921577 |
| 200 | -231.6911202 |
| 210 | -231.6896897 |
| 220 | -231.68825 |
| 230 | -231.6872158 |
| 240 | -231.6869194 |
| 250 | -231.6874974 |
| 260 | -231.6888188 |
| 270 | -231.6904839 |
| 280 | -231.6919257 |
| 290 | -231.6926342 |
| 300 | -231.6923656 |
| 310 | -231.6911713 |
| 320 | -231.6892996 |
| 330 | -231.687116 |
| 340 | -231.6850574 |
| 350 | -231.6835713 |
| 360 | -231.6830255 |
| 10 | -231.6835714 |
| 20 | -231.6850573 |
| 30 | -231.687116 |
| 40 | -231.6892996 |
| 50 | -231.6911713 |
| 60 | -231.6923655 |
| 70 | -231.6926342 |
| 80 | -231.6919257 |
| 90 | -231.6904839 |
| 100 | -231.6888188 |
| 110 | -231.6874974 |
| 120 | -231.6869193 |
| 130 | -231.6872158 |
| 140 | -231.68825 |
| 150 | -231.6896897 |
| 160 | -231.6911203 |
| 170 | -231.6921577 |
| 180 | -231.6925353 |
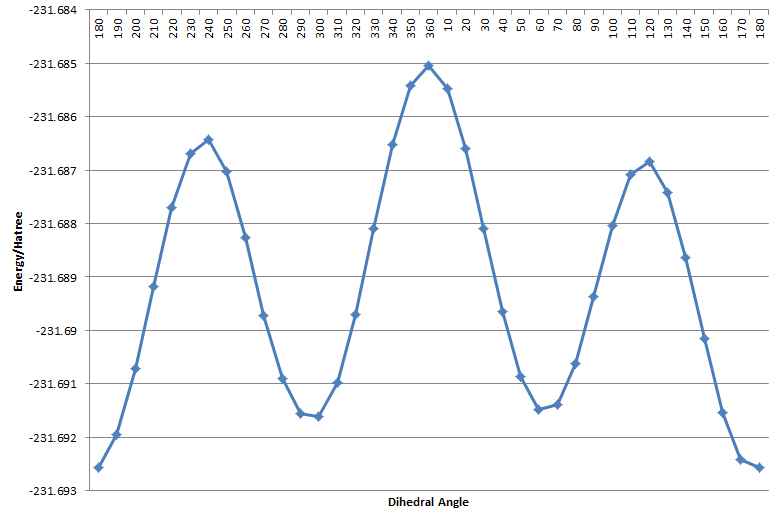
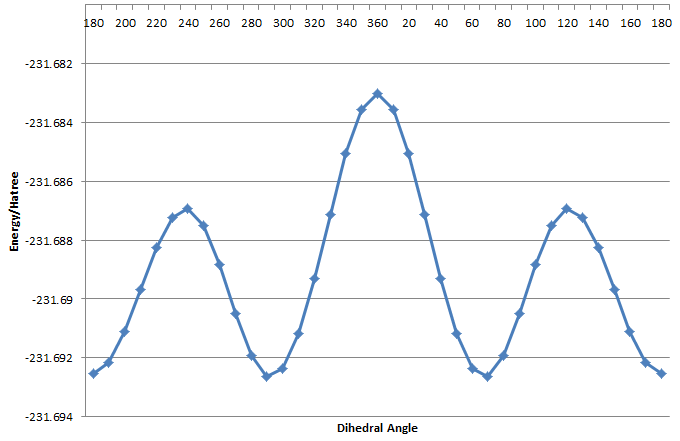
The dihedral scan shows that the conformations with groups elapsing are highest energy structures (the "transition state" to interconversion of conformers. Gauche and anti-periplanar conformations correspond to local minima. For the vinyl groups pointing parallel, the antiperiplanar conformation is the global minimum, and is 2.51kJ/mol lower in energy than the gauche conformer. For the vinyl groups pointing antiparallel, the gauche conformation is the global minimum and is 0.260 kJ/mol lower in energy than the anti-periplanar conformer. 10 low energy conformers are found.
| Conformer | Structure | Point Group | Energy (HF/3-21G)/ Hatree | DOI link |
|---|---|---|---|---|
| Gauche 1 |  |
C2 | -231.68772 | DOI:10042/to-13385 |
| Gauche 2 |  |
C2 | -231.69167 | DOI:10042/to-13386 |
| Gauche 3 |  |
C1 | -231.69266 | DOI:10042/to-13387 |
| Gauche 4 |  |
C2 | -231.69153 | DOI:10042/to-13388 |
| Gauche 5 |  |
C2 | -231.68962 | DOI:10042/to-13389 |
| Gauche 6 | |
C2 | -231.68916 | DOI:10042/to-13391 |
| Anti 1 |  |
C2 | -231.69260 | DOI:10042/to-13392 |
| Anti 2 |  |
Ci | -231.69254 | DOI:10042/to-13395 |
| Anti 3 |  |
C2h | -231.68907 | DOI:10042/to-13396 |
| Anti 4 |  |
C1 | -231.69097 | DOI:10042/to-13397 |
The optimised structure and energies agrees well with those reported in (https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3). The Anti 2 structure is further optimised using B3LYP/6-31G(d) (DOI:10042/to-13394 ), a higher level of theory compared to HF/3-21G. The optimised structure is very similar to that obtained using HF/3-21G. Frequency analysis reveals no negative frequencies, suggesting a stable equilibrium structure has been found. The thermochemical data is calculated for this conformer.
| Energy/Hatree | |
|---|---|
| Sum of electronic and zero-point Energies | -234.469204 |
| Sum of electronic and thermal Energies | -234.461857 |
| Sum of electronic and thermal Enthalpies | -234.460913 |
| Sum of electronic and thermal Free Energies | -234.500777 |
Optimising the Chair-like Transition State
The chair-like transition state is first obtained by placing two allyl fragment together, with the ends of the optimised allyl fragment placed approximately 2.2Â apart. This structure is used as a first guess to the transition state and its optimised to transition state using the Berny algorithm and HF/3-21(G), with force constant calculated once at the beginning. The keyword opt=NoEigen is specified to avoid the calculation halting if more than one imaginary frequency is detected during optimisation. Vibrational analysis confirmed the transition state with one imaginary frequency at -818 cm-1 (DOI:10042/to-13401 ).
Guessed Transition State |
The input guessed chair-like transition state
Vibration |
The transition state with a negative mode of vibration at -818 cm-1 animated.
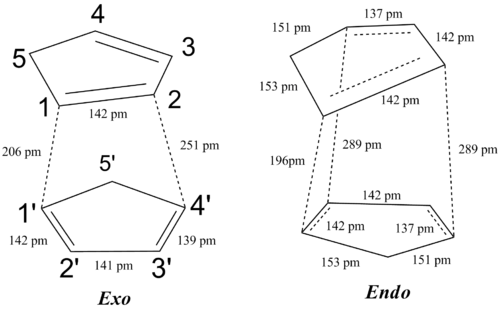
The structure of the transition state has C2h symmetry, with inter-allyl separation of 2.02 Â.
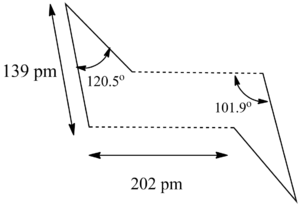
The structure of the transition state is also confirmed by using redundant coordinates. The distance between the allyl fragment is frozen at 2.2 Â and the and the rest of the system is optimised to a minimum using the keyword opt=modredundant (DOI:10042/to-13458 ). The constrain-optimised system is set optimised to transition state using the Berny algorithm. The bond between C3-C4 and C1-C2 is set to derivative to enable calculation of numerical second derivatives for the row and column of the initial Hessian for the coordinates C3-C4 and C1-C2. This increases the accuracy in locating the transition state by scanning the C3-C4 bond length, and C1-C2 bond length coordinates. Frequency analysis showed reveals a transition state which is the same as that obtained by optimizing the "guessed" transition state. (DOI:10042/to-13461 )
Optimising the Boat-like Transition State
The structure of the boat-like transition state is investigated using the quadratic synchronous transit QST2 method. This method assumes the coordinates of the atoms in the transition structure will lie along a parabola connecting the reactant and product geometries, and the algorithm will quadratically interpolate between the product and reactant structure supplied.
The optimised anti 2 conformer is used as the input structure for reactant and product. The atom number is renamed to allow the algorithm to track the bond formed and bond broken. The job failed to converge, with the intermediate optimised transition state structure somewhat similar to the chair transition structure albeit being much looser (DOI:10042/to-13471 ). It is likely to be due the fact that the starting "reactant" geometry is too far from the transition state and therefore even quadratic interpolation between reactant and and product fails to rotate central C-C bond. In order to locate the transition state, a more reasonable reactant and product structure is supplied, with the central C-C-C-C dihedral angle set to 0o (the anti 2 conformer has a C-C-C-C dihedral angle of 180o) and the inside C-C-C angle set to 100o (the anti 2 conformer has inside C-C-C angle of 111o).
This input of reactant and product successfully yield a boat-like transition state of C2v symmetry (DOI:10042/to-13480 ). The transition structure showed a negative mode of vibration at -840cm-1 with an inter-allyl distance of 2.14Â.
Vibration |
The transition state with a negative mode of vibration at -840 cm-1 animated.
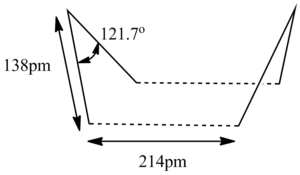
Calculation of Activation Energy
In order to calculate the activation energy of the reaction, the boat-like and chair-like transition structure obtained above is re-optimised using Berny algorithm at B3LYP/6-31G(d). Force constant is calculated at every step to ensure accuracy. The optimized transition structures are geometrically very similar to that obtained using HF/3-21G.
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| Chair TS (DOI:10042/to-13458 ) | -231.6193223 | -231.466698 | -231.461339 | -231.460394 | -231.495203 |
| Boat TS (DOI:10042/to-13471 ) | -231.6028024 | -231.450925 | -231.445297 | -231.444353 | -231.47977 |
| Reactant (anti 2)DOI:10042/to-13490 | -231.6925353 | -231.539539 | -231.532565 | -231.531621 | -231.570911 |
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| Chair TS (DOI:10042/to-13485 ) | -234.556983 | -234.414928 | -234.409006 | -234.408061 | -234.443815 |
| Boat TS (DOI:10042/to-13489 ) | -234.5430931 | 234.402342 | 234.396007 | -234.395063 | 234.431752 |
| Reactant (anti 2) DOI:10042/to-13394 | -234.6117104 | -234.469204 | -234.461857 | -234.460913 | -234.500777 |
From the thermochemical data tabulated above, the activation energy can be calculated at 298.15 K and at 0 K by taking the difference between the sum of electronic and thermal energy of the reactant and transition state at the respective temperature.
| HF/3-21G | HF/3-21G | B3LYP/6-31G | B3LYP/6-31G | Experimental Data | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔEa(chair) | 45.71 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔEa(boat) | 55.61 | 54.76 | 41.96 | 41.32 | 44.7 ± 2.0 |
Intrinsic Reaction Coordinates Analysis
Intrinsic reaction coordination analysis is used to study which conformer the reaction paths from the transitions structures lead to. IRC takes the system down a minimum energy path by following the vectors of the negative vibrational mode whilst optimizing all atomic coordinates orthogonal to it so that. Intrinsic reaction coordinate analysis enables confirmation of whether the transition state actually links the reactants to products. In this case, HF/3-21G theory is used, 50 steps are taken along the IRC with force constants computed once at the beginning.
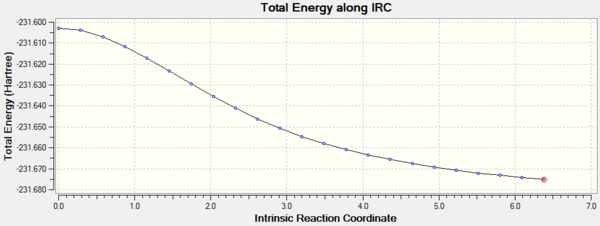
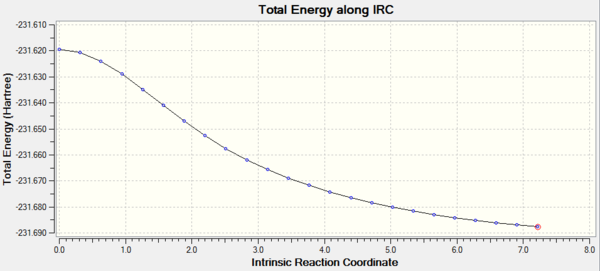
Both IRC paths lead to a structure that does not resemble the low energy conformers obtained above.
| Starting from chair-like TS | Starting from boat-like TS |
 |
|
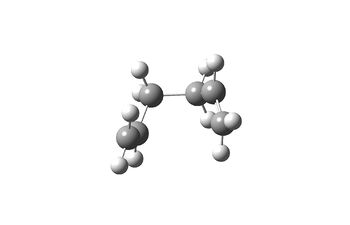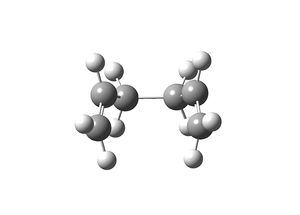
Three approaches has been used to locate the conformer that the IRC leads to. Firstly, the final geometry of the IRC analysis is optimised to a minimum.
Guessed Transition State |
The optimised geometry of the structure taken at the end of 50 steps IRC analysis staring from the boat-like transition state DOI:10042/to-13499
Guessed Transition State |
The optimised geometry of the structure taken at the end of 50 steps IRC analysis staring from the chair-like transition state DOI:10042/to-13498
The chair transition state leads to gauche 2 conformer whereas the boat-like transition state lead to the gauche 3 conformer.
In order to confirm this, 100 steps of IRC calculation is done, starting from the transition state with force constant calculated at every step.
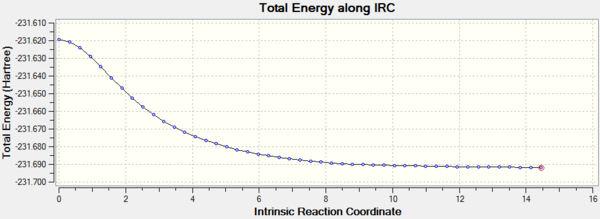
Guessed Transition State |
The final structure of the 100 step IRC analysis staring from the boat-like transition state
Guessed Transition State |
The final structure of the 100 step IRC analysis staring from the chair-like transition state
The 100 steps IRC analysis confirms that the chair transition state leads to gauche 2 conformer whereas the boat-like transition state lead to the gauche 3 conformer. The slight maxima on the IRC curve for the boat conformer suggests another "transition state" for C-C bond rotation.
Diels-Alder Reaction
The Diels-Alder reaction is a thermal [4+2] cycloaddition between a diene and a dieneophile. The reactivity of thermal pericyclic reactions are governed by the Woodward-Hoffmann rule, which states that a pericyclic reaction involving 4n+2 or 4n electrons is thermally allowed if the number of antarafacial components is even or odd, respectively. [14] This is because of symmetry requirement on the HOMO and LUMO of the reactants so as to enable overlap and bond formation. An equivalent statement can be made in terms of transition state aromaticity, which states that the number of electrons participating in a thermal pericyclic reaction must sum to 4n+2 so as to achieve a Hückel aromatic transition state and electron participating in a photochemical pericyclic reaction must sum up to 4n so as to achieve a Möbius transition state. [15] [16]
Prototypical Reaction
In order to investigate the symmetry requirements of the Diels-Alder Reaction, a prototypical Diels-Alder reaction between the hexa-1,3-diene and ethylene is investigated.
The Reactants and Products
The geometry and of the reactants are optimised using HF/3-21G and then optimised using B3LYP/6-31G(d). The diene can interconvert between the s-cis and s-trans conformation, with the s-cis conformation of C2v symmetry being the reactive conformation.
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| s-cis (DOI:10042/to-13527 ) | -155.98594963 | -155.900827 | -155.896786 | -155.895841 | -155.926243 |
| s-trans(DOI:10042/to-13528 ) | -155.99214466 | -155.906654 | -155.902009 | -155.901065 | -155.933100 |
As seen, the s-cis conformation is of a higher energy than s-trans possible because of more steric repulsion in the s-cis conformation relative to the s-trans. The equilibrium between s-cis and s-trans can be estimated using Boltzmann formula
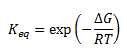
with ΔG calculated from the difference in free energy between s-cis and s-trans. Substituting and converting to kJ/mol, ΔG=18.00 kJ/mol. Hence the equilibrium constant is K=7.01x10-4 in favour of s-trans. Despite the s-cis isomer is the minor conformer in solution, the Diels-Alder reaction forming the stable six membered ring will consume the s-cis conformer and drive the equilibrium towards the s-cis conformer.
The thermochemical data of ethylene calculated using B3LYP/6-31G(d) is:
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies |
|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | |
| -78.58745828 | -78.536232 | -78.533191 | -78.532246 | -78.557762 |
The frontier orbitals of the reactants, which are undergoing change in the Diels-Alder reaction, are analysed using B3LYP/6-31G(d).
The success of the Diels-Alder reaction can be considered in terms of orbital correlation diagram. [17] The system processes a mirror plane that are maintained throughout the reaction, thus orbitals of the reactants and product will be classified in terms of antisymmtric (A) or symmetric (S) with respect to the molecular mirror plane.
The fragment molecular orbital of the σ bonds in the product shown in the above correlation diagram is derived by considering linear combination of the adjacent σ and σ* bonds.
The correlation diagram showed that the electrons from the bonding orbitals of the reactants are mapped into the bonding orbitals of the products. A overall reduction in energy is achieved by the extra π bonding in σ1 and σ2 renders it lower in energy than ψ1 and ψ2.
The Transition State
The transition state is found by optimising the reactants arranged in the trial transition state in accordance with chemical intuition, constraining the distance between terminal carbons of the reactants to 2.2 Â (DOI:10042/to-13531 ) using HF/3-21G. The resultant structure is than optimised to transition state using HF/3-21G, with numerical second derivative evaluated for every step for the two bonds between the terminal carbons of the reactants (DOI:10042/to-13532 ). Vibrational analysis confirmed a negative frequency at -818cm-1. Visualization of the transition mode confirms that it corresponds to the Diels Alder reaction.
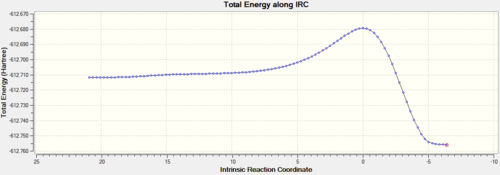
Intrinsic reaction coordinate analysis is performed on the transition state structure, demonstrating the fact that the transition state identified is indeed the transition state linking the reactant to product. The animation along the IRC also shows clearly synchronous bond formation.
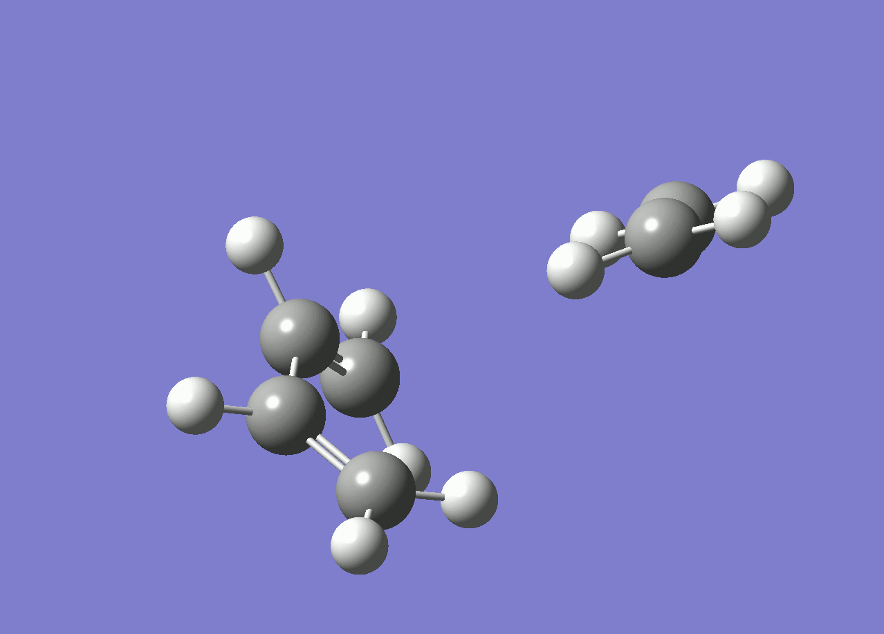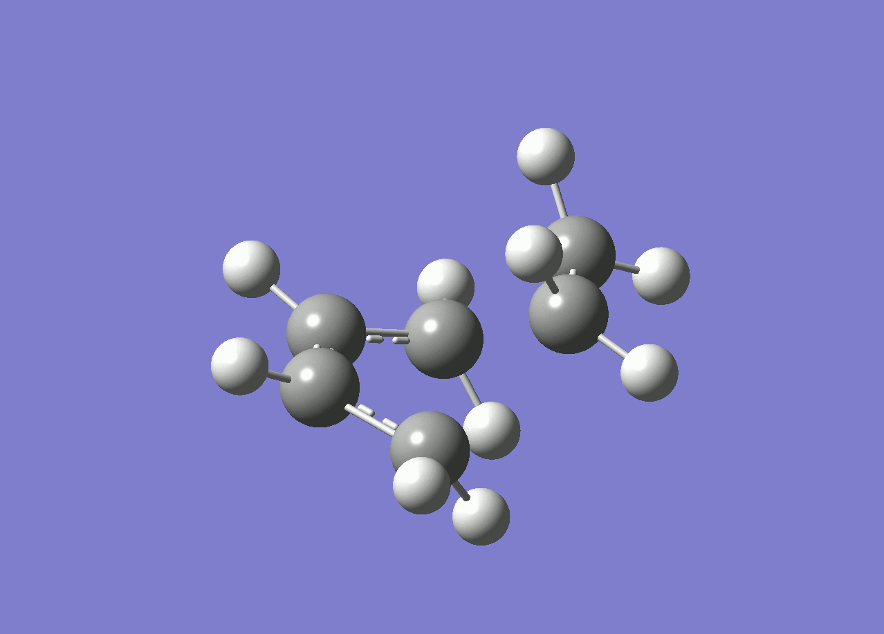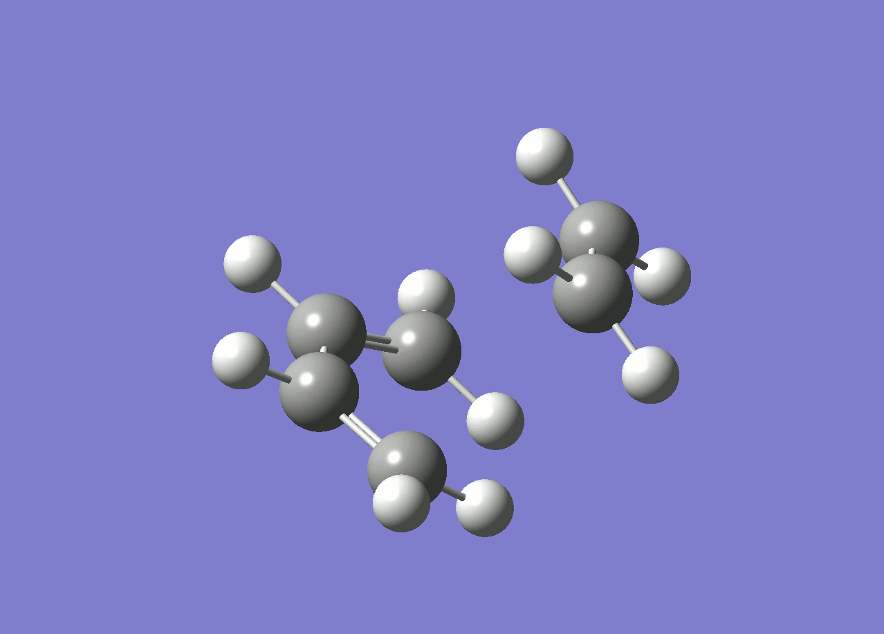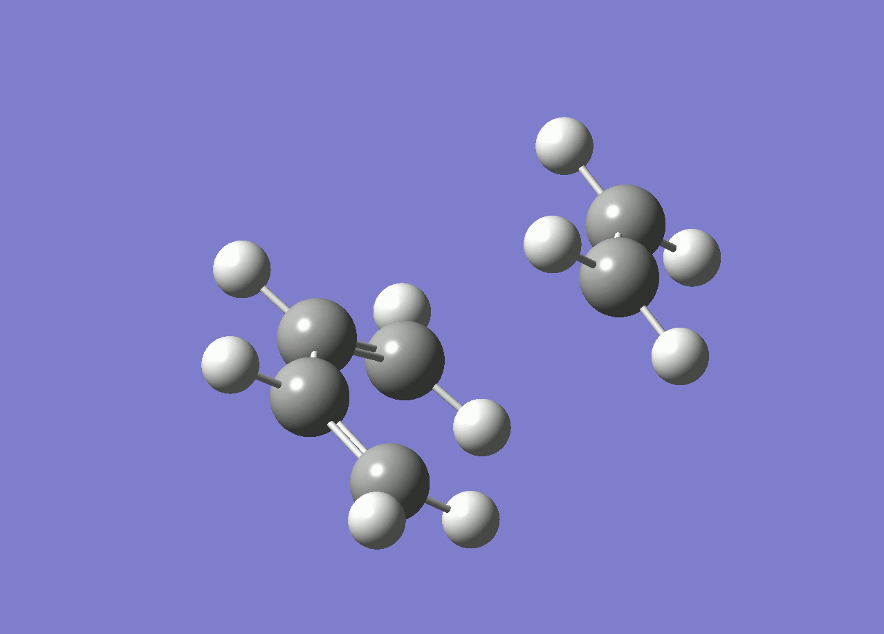
The plot of the energy along the IRC shows that there is only one maximum, corresponding to the transition state. The product (on the left hand side) is of lower energy than the reactant, showing that the reaction is thermodynamically favored.
In order to obtain more accurate thermochemical and structural parameter for the transition state, the transition structure is re-optimised at B3LYP/6-31G(d) using the Berny algorithm. Vibration analysis reveals a negative mode of vibration at -525cm-1, corresponding to the Diels Alder reaction. The imaginary mode correspond to synchronous bond formation, as opposed to the lowest positive mode at 136 cm-1, which suggests asynchronous bond formation.
Vibration |
Animation of the vibration at -525cm-1 DOI:10042/to-13539
Vibration |
Animation of the vibration at 136 cm-1 DOI:10042/to-13539
The transition state is of Cs symmetry. Taking a typical C-C bond length to be around 1.5 Â and a C=C bond to be around 1.3 Â, [18] the C4-C3, C1-C2 and C5-C6 bond is still close to a C=C bond whilst C2-C3 is somewhat shorter than a normal C-C single bond. Comparing with the optimised structure of butadiene and ethylene, the C4-C3, C1-C2 bond length in in butadiene is 1.36 Â, showing that the C=C character is not diminished to any significant extent in the transition state. The C2-C3 bond length, however, changes from 1.54 Â in butadiene to 1.41 Â in the transition state, showing significant bond shortening and double bond character. The C5-C6 bond length in the transition state doe not deviate significantly from 1.36 Â, the C=C bond length in optimised ethylene. The C5-C4, and C1-C6 bond lengths are much longer than a C-C single bond but nonetheless still shorter than the sum of van der Waals radius of two carbons, which is 3.4Â.[19] This shows some degree of C-C bonding between C5-C4, and C1-C6 in the transition state.
The angle of approach of the ethylene molecule is 102.3o, this is similar to the Burgi-Dunitz angle in nucleophilic attack of carbonyl group [20] and has origin in effective overlap of the ethylene π orbital with the buta-1,3-diene π orbital.
This thermal pericyclic reaction is allowed as the HOMO of the diene and the LUMO of the dienophile, and the LUMO of the diene and the HOMO of the dienophile have the same symmetry. Evidently, the reaction is promoted by decreasing energy difference between the interacting orbitals, and experimentally Diels Alder reaction is driven by the diene and dienophile having complementary electronic demands.
Thermochemical data are computed from B3LYP/6-31G(d) for the transition state.
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies |
|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | |
| -234.54389656 | -234.403324 | -234.396906 | -234.395962 | -234.432891 |
The activation energy is calculated by taken the difference between reactant and transition state energies, i.e.
The activation energy is 88.57 kJ/mol at 0K and 86.83 kJ/mol at 298.15 K.
Reaction between Cyclohexa-1,3-diene and Maleic Anhydride
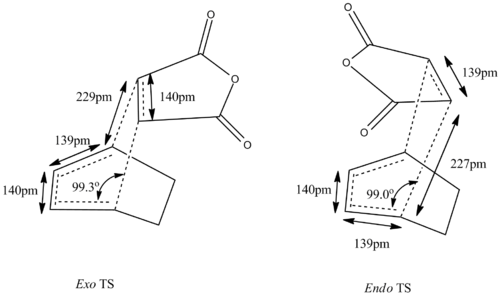
The Diels Alder reaction between maleic anhydride and cyclohexa-1,3-diene introduces an extra aspect of endo/exo selectivity depending on the orientation of the maleic anhydride in the transition state.
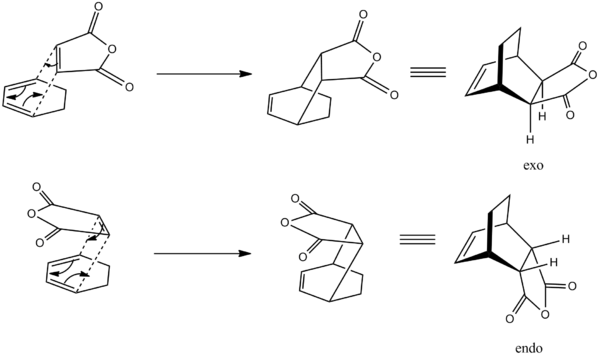
The Products and Reactants
The geometry of the reactants are optimised using B3LYP/6-31g(d). Vibrational analysis confirms that a minimum has been reached. Thermochemical data are tabulated below:
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| Maleic anhydride (DOI:10042/to-13555 ) | -379.28954456 | -379.233656 | -379.228472 | -379.227528 | -379.262730 |
| Cyclohexa-1,3-diene(DOI:10042/to-13556 ) | -233.41893632 | -233.296105 | -233.290933 | -233.289988 | -233.324356 |
Molecular orbital analysis shows that compared to the previous reaction of butadiene with ethylene, there are better energy match between the LUMO of maleic anhydride and HOMO of cyclohexa-1,3-diene but significantly larger energy disparity between the relevant π orbital on maleic anhydride (HOMO-2) and the LUMO of cyclohexa-1,3-diene. The presence of electron withdrawing anhydride functionality lowers the energy of both π and π*. However, all in all, the reaction is more favoured compared to reaction of butadiene with ethylene. This is because following a Klopman-Salem equation, which states that that the energy of two orbiatls interaction with each other is inversely proportional to their energy difference, one "strong" interaction and one "weak" interaction is favored over two "medium" interaction.
The Transition State
The transition state was found by the first optimising the "guessed" endo (DOI:10042/to-13621 ) and exo (DOI:10042/to-13622 )transition state to equilibrium, holding the terminal carbons of cyclohexa-1,3-diene and maleic anhydride to 2.2 Â, at HF/3-21 level. The equilibrium geometry is then reoptimized to transition state by HF/3-21G, evaluating numerical second derivative for the two C-C bond between maleic anhydride and cyclohexa-1,3-diene. Vibrational analysis reveals that a transition state has been reached with negative vibrational frequency of -645 cm-1 for the endo case (DOI:10042/to-13624 ) and -647cm-1 for the exo case (DOI:10042/to-13628 ).
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| exo Transition state | -605.60535492 | -605.408138 | -605.398680 | -605.397735 | -605.443681 |
| endo Transition state' | -605.61036830 | -605.414902 | -605.405477 | -605.404533 | -605.450129 |
| E(endo)-E(exo)/kJmol-1 | -13.16 | -17.76 | -17.85 | -17.85 | -16.93 |
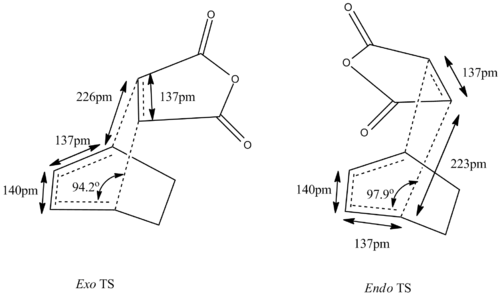
The transition states are then optimised using B3LYP/6-31G(d), a higher level of theory and a larger basis set, in order to obtain more accurate thermochemical and structural data. IRC analysis at B3LYP/6-31G(d)provides direct visualisation of the synchronous formation of the two C-C bonds.
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| exo Transition state (DOI:10042/to-13630 ) | -612.67931091 | -612.498011 | -612.487660 | -612.486716 | -612.534264 |
| endo Transition state'(DOI:10042/to-13631 ) | -612.68339670 | -612.502142 | -612.491788 | -612.490844 | -612.538330 |
| E(endo)-E(exo)/kJmol-1 | -10.73 | -10.85 | -10.84 | -10.84 | -10.68 |
Vibration |
Animation of the endo transition state
Vibration |
Animation of the exo transition state
| IRC animation | Energy along IRC Path | |
|---|---|---|
| exo DOI:10042/to-13708 |  |
|
| endo DOI:10042/to-13707 |  |
|
Despite the structural similarity between the HF/3-21G optimised and B3LYP/6-31G(d) optimised structure, the energy difference predicted for endo and exo transition states are very different. Suggesting that in order that higher level of theory is conducive to obtaining better thermochemical data but optimised geometry from a lower level is a good starting point for high level calculations.
The geometric features of the transition state is similar to the prototypical reaction analysed above. The transition state is of Cs symmetry. Taking a typical C-C bond length to be around 1.5 Â and a C=C bond to be around 1.3 Â, the C4-C3, C1-C2 and C5-C6 bond is still close to a C=C bond whilst C2-C3 is somewhat shorter than a normal C-C single bond. Comparing with the optimised structure of cyclohexa-1,3-diene and maleic anhydride, the C4-C3, C1-C2 bond length in cyclohexa-1,3-diene is 1.39 Â, showing that the C=C character is not diminished to any significant extent in the transition state. The C5-C6 bond length in the transition state does not deviate significantly from 1.35 Â, the C=C bond length in optimised maleic anhydride. The C5-C4, and C1-C6 bond lengths are much longer than a C-C single bond but nonetheless still shorter than the sum of van der Waals radius of two carbons, which is 3.4Â. This shows some degree of C-C bonding between C5-C4, and C1-C6 in the transition state.
The endo transition state is of lower energy than the exo transition state. The "traditional" rationalisation is based on the so-called secondary orbital overlap pioneered by Woodward and Hoffmann. [14] In this theory, the endo transition state is stablised by secondary π overlap between the carbonyl carbon and the diene that is present in the endo transition state but not in the exo diene.
Visualization of the molecular orbitals reveals some secondary orbital interactions in the HOMO, between the oxygen lone pair of anti-symmetric character and the HOMO of the diene. However, some interaction between the carbonyl carbons and the diene, and between the anhydride oxygen and the diene are found in the lower energy MOs in the endo transition state, which are absent in the exo transition state.
| HOMO | Interaction between carbonyl carbons and diene | Interaction between anhydride oxygen and diene |
|---|---|---|
 |
 |
|
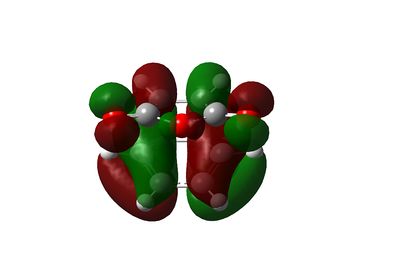The secondary orbital interactions can be further quantified using natural bonding orbital analysis. For the endo transition state, the interactions between anhydride oxygen and diene is absent from NBO analysis and the carbonyl and dienophile interaction, used by Woodward and Hoffmann as a rationalisation of the endo selectivity, is rather weak (summing to only 3.12 kcal/mol). However, another secondary orbital interaction of Cieplak (σ->π*) type is identified between the C-H bond in maleic anhydride and the diene, summing to 6.02 kcal/mol. However, those interactions are rather weak. The NBO output, shown below, reveals only weak interaction from diene (unit 1) to dieneophile (unit 2) and from dieneophile (unit 2) to diene (unit 1) except the interactions corresponding to the forming C-C bond.
from unit 1 to unit 2 1. BD ( 1) C 1 - H 2 /129. RY*( 6) C 14 0.06 1.78 0.009 1. BD ( 1) C 1 - H 2 /208. BD*( 2) C 14 - O 16 0.11 0.54 0.007 3. BD ( 1) C 1 - C 9 / 81. RY*( 1) C 7 0.26 1.88 0.020 3. BD ( 1) C 1 - C 9 / 82. RY*( 2) C 7 0.38 1.62 0.022 3. BD ( 1) C 1 - C 9 / 83. RY*( 3) C 7 0.26 1.84 0.019 3. BD ( 1) C 1 - C 9 /129. RY*( 6) C 14 0.13 1.97 0.015 3. BD ( 1) C 1 - C 9 /197. BD*( 2) C 5 - C 7 0.83 0.72 0.024 4. BD ( 2) C 1 - C 9 / 83. RY*( 3) C 7 0.59 1.39 0.028 4. BD ( 2) C 1 - C 9 / 84. RY*( 4) C 7 0.13 1.89 0.016 4. BD ( 2) C 1 - C 9 / 87. RY*( 7) C 7 0.09 2.20 0.014 4. BD ( 2) C 1 - C 9 /197. BD*( 2) C 5 - C 7 15.91 0.27 0.058 4. BD ( 2) C 1 - C 9 /200. BD*( 1) C 7 - C 14 0.11 0.68 0.008 4. BD ( 2) C 1 - C 9 /208. BD*( 2) C 14 - O 16 1.56 0.28 0.019 5. BD ( 1) C 3 - H 4 /139. RY*( 6) C 15 0.06 1.78 0.009 5. BD ( 1) C 3 - H 4 /210. BD*( 2) C 15 - O 17 0.11 0.54 0.007 6. BD ( 1) C 3 - C 10 / 70. RY*( 1) C 5 0.26 1.88 0.020 6. BD ( 1) C 3 - C 10 / 71. RY*( 2) C 5 0.38 1.62 0.022 6. BD ( 1) C 3 - C 10 / 72. RY*( 3) C 5 0.26 1.84 0.019 6. BD ( 1) C 3 - C 10 /139. RY*( 6) C 15 0.13 1.97 0.015 6. BD ( 1) C 3 - C 10 /197. BD*( 2) C 5 - C 7 0.83 0.72 0.024 7. BD ( 2) C 3 - C 10 / 72. RY*( 3) C 5 0.59 1.39 0.028 7. BD ( 2) C 3 - C 10 / 73. RY*( 4) C 5 0.13 1.89 0.016 7. BD ( 2) C 3 - C 10 / 76. RY*( 7) C 5 0.09 2.20 0.014 7. BD ( 2) C 3 - C 10 /197. BD*( 2) C 5 - C 7 15.91 0.27 0.058 7. BD ( 2) C 3 - C 10 /198. BD*( 1) C 5 - C 15 0.11 0.68 0.008 7. BD ( 2) C 3 - C 10 /210. BD*( 2) C 15 - O 17 1.56 0.28 0.019 14. BD ( 1) C 9 - H 11 / 83. RY*( 3) C 7 0.35 1.66 0.022 14. BD ( 1) C 9 - H 11 / 84. RY*( 4) C 7 0.05 2.17 0.010 14. BD ( 1) C 9 - H 11 /196. BD*( 1) C 5 - C 7 0.08 1.08 0.008 14. BD ( 1) C 9 - H 11 /197. BD*( 2) C 5 - C 7 1.11 0.54 0.024 15. BD ( 1) C 9 - C 21 / 81. RY*( 1) C 7 0.33 1.80 0.022 15. BD ( 1) C 9 - C 21 / 82. RY*( 2) C 7 0.20 1.54 0.016 15. BD ( 1) C 9 - C 21 / 83. RY*( 3) C 7 0.58 1.76 0.029 15. BD ( 1) C 9 - C 21 / 91. RY*( 1) H 8 0.07 1.23 0.008 15. BD ( 1) C 9 - C 21 /197. BD*( 2) C 5 - C 7 1.55 0.64 0.031 16. BD ( 1) C 10 - H 12 / 72. RY*( 3) C 5 0.35 1.66 0.022 16. BD ( 1) C 10 - H 12 / 73. RY*( 4) C 5 0.05 2.17 0.010 16. BD ( 1) C 10 - H 12 /196. BD*( 1) C 5 - C 7 0.08 1.08 0.008 16. BD ( 1) C 10 - H 12 /197. BD*( 2) C 5 - C 7 1.11 0.54 0.024 17. BD ( 1) C 10 - C 18 / 70. RY*( 1) C 5 0.33 1.80 0.022 17. BD ( 1) C 10 - C 18 / 71. RY*( 2) C 5 0.20 1.54 0.016 17. BD ( 1) C 10 - C 18 / 72. RY*( 3) C 5 0.58 1.76 0.029 17. BD ( 1) C 10 - C 18 / 80. RY*( 1) H 6 0.07 1.23 0.008 17. BD ( 1) C 10 - C 18 /197. BD*( 2) C 5 - C 7 1.55 0.64 0.031 24. BD ( 1) C 18 - H 19 / 70. RY*( 1) C 5 0.14 1.68 0.014 24. BD ( 1) C 18 - H 19 / 71. RY*( 2) C 5 0.06 1.42 0.008 24. BD ( 1) C 18 - H 19 /195. BD*( 1) C 5 - H 6 0.12 0.98 0.010 24. BD ( 1) C 18 - H 19 /198. BD*( 1) C 5 - C 15 0.10 0.93 0.009 25. BD ( 1) C 18 - H 20 / 70. RY*( 1) C 5 0.09 1.67 0.011 26. BD ( 1) C 18 - C 21 / 70. RY*( 1) C 5 0.12 1.76 0.013 26. BD ( 1) C 18 - C 21 / 81. RY*( 1) C 7 0.12 1.76 0.013 27. BD ( 1) C 21 - H 22 / 81. RY*( 1) C 7 0.14 1.68 0.014 27. BD ( 1) C 21 - H 22 / 82. RY*( 2) C 7 0.06 1.42 0.008 27. BD ( 1) C 21 - H 22 /199. BD*( 1) C 7 - H 8 0.12 0.98 0.010 27. BD ( 1) C 21 - H 22 /200. BD*( 1) C 7 - C 14 0.10 0.93 0.009 28. BD ( 1) C 21 - H 23 / 81. RY*( 1) C 7 0.09 1.67 0.011 33. CR ( 1) C 9 / 83. RY*( 3) C 7 0.06 11.21 0.023 33. CR ( 1) C 9 /197. BD*( 2) C 5 - C 7 0.37 10.09 0.061 34. CR ( 1) C 10 / 72. RY*( 3) C 5 0.06 11.21 0.023 34. CR ( 1) C 10 /197. BD*( 2) C 5 - C 7 0.37 10.09 0.061 191. BD*( 2) C 1 - C 9 / 83. RY*( 3) C 7 0.07 1.11 0.022 191. BD*( 2) C 1 - C 9 /199. BD*( 1) C 7 - H 8 0.12 0.45 0.017 191. BD*( 2) C 1 - C 9 /205. BD*( 1) O 13 - C 14 0.08 0.29 0.010 194. BD*( 2) C 3 - C 10 / 72. RY*( 3) C 5 0.07 1.11 0.022 194. BD*( 2) C 3 - C 10 /195. BD*( 1) C 5 - H 6 0.12 0.45 0.017 194. BD*( 2) C 3 - C 10 /206. BD*( 1) O 13 - C 15 0.08 0.29 0.010
from unit 2 to unit 1 8. BD ( 1) C 5 - H 6 / 61. RY*( 3) C 3 0.05 1.42 0.008 8. BD ( 1) C 5 - H 6 /104. RY*( 3) C 10 0.38 1.58 0.022 8. BD ( 1) C 5 - H 6 /105. RY*( 4) C 10 0.21 2.08 0.019 8. BD ( 1) C 5 - H 6 /165. RY*( 2) C 18 0.12 1.43 0.012 8. BD ( 1) C 5 - H 6 /193. BD*( 1) C 3 - C 10 0.08 1.12 0.008 8. BD ( 1) C 5 - H 6 /194. BD*( 2) C 3 - C 10 3.02 0.57 0.040 8. BD ( 1) C 5 - H 6 /204. BD*( 1) C 10 - C 18 0.06 0.95 0.007 8. BD ( 1) C 5 - H 6 /211. BD*( 1) C 18 - H 19 0.07 1.00 0.008 8. BD ( 1) C 5 - H 6 /212. BD*( 1) C 18 - H 20 0.11 0.99 0.009 9. BD ( 1) C 5 - C 7 / 50. RY*( 3) C 1 0.06 1.58 0.008 9. BD ( 1) C 5 - C 7 / 61. RY*( 3) C 3 0.06 1.58 0.008 9. BD ( 1) C 5 - C 7 / 92. RY*( 1) C 9 0.15 1.90 0.015 9. BD ( 1) C 5 - C 7 / 93. RY*( 2) C 9 0.17 1.48 0.014 9. BD ( 1) C 5 - C 7 /102. RY*( 1) C 10 0.15 1.90 0.015 9. BD ( 1) C 5 - C 7 /103. RY*( 2) C 10 0.17 1.48 0.014 9. BD ( 1) C 5 - C 7 /164. RY*( 1) C 18 0.05 1.73 0.009 9. BD ( 1) C 5 - C 7 /176. RY*( 1) C 21 0.05 1.73 0.009 9. BD ( 1) C 5 - C 7 /191. BD*( 2) C 1 - C 9 0.70 0.74 0.022 9. BD ( 1) C 5 - C 7 /194. BD*( 2) C 3 - C 10 0.70 0.74 0.022 10. BD ( 2) C 5 - C 7 / 94. RY*( 3) C 9 0.48 1.30 0.024 10. BD ( 2) C 5 - C 7 / 95. RY*( 4) C 9 0.14 1.79 0.015 10. BD ( 2) C 5 - C 7 / 96. RY*( 5) C 9 0.06 2.30 0.011 10. BD ( 2) C 5 - C 7 / 99. RY*( 8) C 9 0.09 2.27 0.014 10. BD ( 2) C 5 - C 7 /104. RY*( 3) C 10 0.48 1.30 0.024 10. BD ( 2) C 5 - C 7 /105. RY*( 4) C 10 0.14 1.79 0.015 10. BD ( 2) C 5 - C 7 /106. RY*( 5) C 10 0.06 2.30 0.011 10. BD ( 2) C 5 - C 7 /109. RY*( 8) C 10 0.09 2.27 0.014 10. BD ( 2) C 5 - C 7 /191. BD*( 2) C 1 - C 9 10.32 0.29 0.049 10. BD ( 2) C 5 - C 7 /194. BD*( 2) C 3 - C 10 10.32 0.29 0.049 10. BD ( 2) C 5 - C 7 /202. BD*( 1) C 9 - C 21 0.18 0.66 0.011 10. BD ( 2) C 5 - C 7 /204. BD*( 1) C 10 - C 18 0.18 0.66 0.011 10. BD ( 2) C 5 - C 7 /212. BD*( 1) C 18 - H 20 0.32 0.71 0.015 10. BD ( 2) C 5 - C 7 /215. BD*( 1) C 21 - H 23 0.32 0.71 0.015 11. BD ( 1) C 5 - C 15 / 61. RY*( 3) C 3 0.11 1.54 0.012 11. BD ( 1) C 5 - C 15 /103. RY*( 2) C 10 0.20 1.43 0.015 11. BD ( 1) C 5 - C 15 /104. RY*( 3) C 10 0.41 1.71 0.024 11. BD ( 1) C 5 - C 15 /105. RY*( 4) C 10 0.17 2.20 0.017 11. BD ( 1) C 5 - C 15 /164. RY*( 1) C 18 0.12 1.69 0.013 11. BD ( 1) C 5 - C 15 /165. RY*( 2) C 18 0.12 1.55 0.012 11. BD ( 1) C 5 - C 15 /168. RY*( 5) C 18 0.06 2.50 0.011 11. BD ( 1) C 5 - C 15 /194. BD*( 2) C 3 - C 10 0.75 0.69 0.022 12. BD ( 1) C 7 - H 8 / 50. RY*( 3) C 1 0.05 1.42 0.008 12. BD ( 1) C 7 - H 8 / 94. RY*( 3) C 9 0.38 1.58 0.022 12. BD ( 1) C 7 - H 8 / 95. RY*( 4) C 9 0.21 2.08 0.019 12. BD ( 1) C 7 - H 8 /177. RY*( 2) C 21 0.12 1.43 0.012 12. BD ( 1) C 7 - H 8 /190. BD*( 1) C 1 - C 9 0.08 1.12 0.008 12. BD ( 1) C 7 - H 8 /191. BD*( 2) C 1 - C 9 3.02 0.57 0.040 12. BD ( 1) C 7 - H 8 /202. BD*( 1) C 9 - C 21 0.06 0.95 0.007 12. BD ( 1) C 7 - H 8 /214. BD*( 1) C 21 - H 22 0.07 1.00 0.008 12. BD ( 1) C 7 - H 8 /215. BD*( 1) C 21 - H 23 0.11 0.99 0.009 13. BD ( 1) C 7 - C 14 / 50. RY*( 3) C 1 0.11 1.54 0.012 13. BD ( 1) C 7 - C 14 / 93. RY*( 2) C 9 0.20 1.43 0.015 13. BD ( 1) C 7 - C 14 / 94. RY*( 3) C 9 0.41 1.71 0.024 13. BD ( 1) C 7 - C 14 / 95. RY*( 4) C 9 0.17 2.20 0.017 13. BD ( 1) C 7 - C 14 /176. RY*( 1) C 21 0.12 1.69 0.013 13. BD ( 1) C 7 - C 14 /177. RY*( 2) C 21 0.12 1.55 0.012 13. BD ( 1) C 7 - C 14 /180. RY*( 5) C 21 0.06 2.50 0.011 13. BD ( 1) C 7 - C 14 /191. BD*( 2) C 1 - C 9 0.75 0.69 0.022 21. BD ( 2) C 14 - O 16 /202. BD*( 1) C 9 - C 21 0.08 0.77 0.007 23. BD ( 2) C 15 - O 17 /204. BD*( 1) C 10 - C 18 0.08 0.77 0.007 31. CR ( 1) C 5 /104. RY*( 3) C 10 0.06 11.11 0.023 31. CR ( 1) C 5 /194. BD*( 2) C 3 - C 10 0.41 10.10 0.062 32. CR ( 1) C 7 / 94. RY*( 3) C 9 0.06 11.11 0.023 32. CR ( 1) C 7 /191. BD*( 2) C 1 - C 9 0.42 10.10 0.062 43. LP ( 2) O 13 /191. BD*( 2) C 1 - C 9 0.24 0.34 0.008 43. LP ( 2) O 13 /194. BD*( 2) C 3 - C 10 0.24 0.34 0.008 197. BD*( 2) C 5 - C 7 / 94. RY*( 3) C 9 0.10 1.02 0.021 197. BD*( 2) C 5 - C 7 / 95. RY*( 4) C 9 0.06 1.52 0.020 197. BD*( 2) C 5 - C 7 /104. RY*( 3) C 10 0.10 1.02 0.021 197. BD*( 2) C 5 - C 7 /105. RY*( 4) C 10 0.06 1.52 0.020 197. BD*( 2) C 5 - C 7 /191. BD*( 2) C 1 - C 9 118.98 0.01 0.059 197. BD*( 2) C 5 - C 7 /194. BD*( 2) C 3 - C 10 118.98 0.01 0.059 197. BD*( 2) C 5 - C 7 /202. BD*( 1) C 9 - C 21 0.08 0.39 0.011 197. BD*( 2) C 5 - C 7 /204. BD*( 1) C 10 - C 18 0.08 0.39 0.011 197. BD*( 2) C 5 - C 7 /212. BD*( 1) C 18 - H 20 0.07 0.43 0.011 197. BD*( 2) C 5 - C 7 /215. BD*( 1) C 21 - H 23 0.07 0.43 0.011
| Donor Orbital | Acceptor Orbital | Interaction Energy/kcal mol-1 |
|---|---|---|
 |
 |
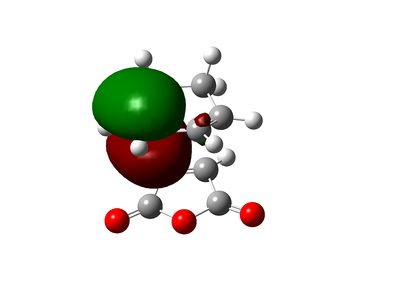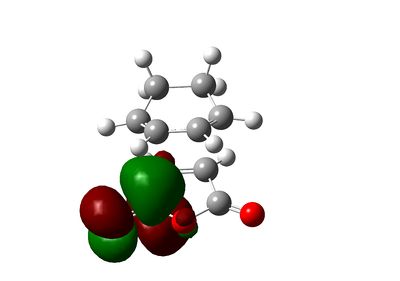1.56 |
 |
 |
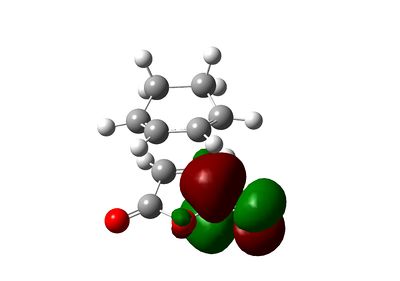1.56 |
 |
 |
3.02 |
 |
 |
3.02 |
Performing the NBO analysis on the exo transition state shows the absence of carbonyl-diene secondary orbital overlap.
from unit 1 to unit 2 2. BD ( 1) C 1 - C 3 / 70. RY*( 1) C 5 0.08 1.93 0.011 2. BD ( 1) C 1 - C 3 / 72. RY*( 3) C 5 0.08 1.76 0.010 2. BD ( 1) C 1 - C 3 / 81. RY*( 1) C 7 0.08 1.93 0.011 2. BD ( 1) C 1 - C 3 / 83. RY*( 3) C 7 0.08 1.76 0.010 3. BD ( 1) C 1 - C 9 / 82. RY*( 2) C 7 0.22 1.51 0.016 3. BD ( 1) C 1 - C 9 / 83. RY*( 3) C 7 0.66 1.78 0.031 3. BD ( 1) C 1 - C 9 / 84. RY*( 4) C 7 0.07 2.30 0.011 3. BD ( 1) C 1 - C 9 / 91. RY*( 1) H 8 0.06 1.29 0.008 3. BD ( 1) C 1 - C 9 /129. RY*( 6) C 14 0.05 1.94 0.009 3. BD ( 1) C 1 - C 9 /197. BD*( 2) C 5 - C 7 0.84 0.72 0.024 4. BD ( 2) C 1 - C 9 / 83. RY*( 3) C 7 0.84 1.32 0.033 4. BD ( 2) C 1 - C 9 / 84. RY*( 4) C 7 0.20 1.84 0.019 4. BD ( 2) C 1 - C 9 / 87. RY*( 7) C 7 0.08 2.19 0.013 4. BD ( 2) C 1 - C 9 /197. BD*( 2) C 5 - C 7 18.05 0.26 0.062 4. BD ( 2) C 1 - C 9 /199. BD*( 1) C 7 - H 8 0.09 0.74 0.008 6. BD ( 1) C 3 - C 10 / 71. RY*( 2) C 5 0.22 1.51 0.016 6. BD ( 1) C 3 - C 10 / 72. RY*( 3) C 5 0.66 1.78 0.031 6. BD ( 1) C 3 - C 10 / 73. RY*( 4) C 5 0.07 2.30 0.011 6. BD ( 1) C 3 - C 10 / 80. RY*( 1) H 6 0.06 1.29 0.008 6. BD ( 1) C 3 - C 10 /139. RY*( 6) C 15 0.05 1.94 0.009 6. BD ( 1) C 3 - C 10 /197. BD*( 2) C 5 - C 7 0.84 0.72 0.024 7. BD ( 2) C 3 - C 10 / 72. RY*( 3) C 5 0.84 1.32 0.033 7. BD ( 2) C 3 - C 10 / 73. RY*( 4) C 5 0.20 1.84 0.019 7. BD ( 2) C 3 - C 10 / 76. RY*( 7) C 5 0.08 2.19 0.013 7. BD ( 2) C 3 - C 10 /195. BD*( 1) C 5 - H 6 0.09 0.74 0.008 7. BD ( 2) C 3 - C 10 /197. BD*( 2) C 5 - C 7 18.05 0.26 0.062 14. BD ( 1) C 9 - H 11 / 82. RY*( 2) C 7 0.07 1.33 0.009 14. BD ( 1) C 9 - H 11 / 83. RY*( 3) C 7 0.32 1.60 0.020 14. BD ( 1) C 9 - H 11 / 84. RY*( 4) C 7 0.07 2.12 0.011 14. BD ( 1) C 9 - H 11 /196. BD*( 1) C 5 - C 7 0.07 1.08 0.008 14. BD ( 1) C 9 - H 11 /197. BD*( 2) C 5 - C 7 1.05 0.54 0.024 15. BD ( 1) C 9 - C 21 / 81. RY*( 1) C 7 0.52 1.87 0.028 15. BD ( 1) C 9 - C 21 / 82. RY*( 2) C 7 0.16 1.42 0.014 15. BD ( 1) C 9 - C 21 / 83. RY*( 3) C 7 0.21 1.69 0.017 15. BD ( 1) C 9 - C 21 / 84. RY*( 4) C 7 0.05 2.21 0.010 15. BD ( 1) C 9 - C 21 /129. RY*( 6) C 14 0.15 1.86 0.015 15. BD ( 1) C 9 - C 21 /197. BD*( 2) C 5 - C 7 1.27 0.63 0.028 15. BD ( 1) C 9 - C 21 /208. BD*( 2) C 14 - O 16 0.05 0.64 0.006 16. BD ( 1) C 10 - H 12 / 71. RY*( 2) C 5 0.07 1.33 0.009 16. BD ( 1) C 10 - H 12 / 72. RY*( 3) C 5 0.32 1.60 0.020 16. BD ( 1) C 10 - H 12 / 73. RY*( 4) C 5 0.07 2.12 0.011 16. BD ( 1) C 10 - H 12 /196. BD*( 1) C 5 - C 7 0.07 1.08 0.008 16. BD ( 1) C 10 - H 12 /197. BD*( 2) C 5 - C 7 1.05 0.54 0.024 17. BD ( 1) C 10 - C 18 / 70. RY*( 1) C 5 0.52 1.87 0.028 17. BD ( 1) C 10 - C 18 / 71. RY*( 2) C 5 0.16 1.42 0.014 17. BD ( 1) C 10 - C 18 / 72. RY*( 3) C 5 0.21 1.69 0.017 17. BD ( 1) C 10 - C 18 / 73. RY*( 4) C 5 0.05 2.21 0.010 17. BD ( 1) C 10 - C 18 /139. RY*( 6) C 15 0.15 1.86 0.015 17. BD ( 1) C 10 - C 18 /197. BD*( 2) C 5 - C 7 1.27 0.63 0.028 17. BD ( 1) C 10 - C 18 /210. BD*( 2) C 15 - O 17 0.05 0.64 0.006 24. BD ( 1) C 18 - H 19 /139. RY*( 6) C 15 0.07 1.73 0.010 24. BD ( 1) C 18 - H 19 /206. BD*( 1) O 13 - C 15 0.09 0.81 0.008 24. BD ( 1) C 18 - H 19 /210. BD*( 2) C 15 - O 17 0.66 0.51 0.017 25. BD ( 1) C 18 - H 20 / 70. RY*( 1) C 5 0.05 1.74 0.009 25. BD ( 1) C 18 - H 20 /210. BD*( 2) C 15 - O 17 0.09 0.51 0.006 27. BD ( 1) C 21 - H 22 /129. RY*( 6) C 14 0.07 1.73 0.010 27. BD ( 1) C 21 - H 22 /205. BD*( 1) O 13 - C 14 0.09 0.81 0.008 27. BD ( 1) C 21 - H 22 /208. BD*( 2) C 14 - O 16 0.66 0.51 0.017 28. BD ( 1) C 21 - H 23 / 81. RY*( 1) C 7 0.05 1.74 0.009 28. BD ( 1) C 21 - H 23 /208. BD*( 2) C 14 - O 16 0.09 0.51 0.006 33. CR ( 1) C 9 / 83. RY*( 3) C 7 0.06 11.15 0.023 33. CR ( 1) C 9 /197. BD*( 2) C 5 - C 7 0.33 10.09 0.057 34. CR ( 1) C 10 / 72. RY*( 3) C 5 0.06 11.15 0.023 34. CR ( 1) C 10 /197. BD*( 2) C 5 - C 7 0.33 10.09 0.057 191. BD*( 2) C 1 - C 9 / 83. RY*( 3) C 7 0.06 1.05 0.019 191. BD*( 2) C 1 - C 9 /199. BD*( 1) C 7 - H 8 0.06 0.46 0.013 191. BD*( 2) C 1 - C 9 /200. BD*( 1) C 7 - C 14 0.22 0.40 0.021 194. BD*( 2) C 3 - C 10 / 72. RY*( 3) C 5 0.06 1.05 0.019 194. BD*( 2) C 3 - C 10 /195. BD*( 1) C 5 - H 6 0.06 0.46 0.013 194. BD*( 2) C 3 - C 10 /198. BD*( 1) C 5 - C 15 0.22 0.40 0.021
from unit 2 to unit 1 8. BD ( 1) C 5 - H 6 / 61. RY*( 3) C 3 0.13 1.36 0.012 8. BD ( 1) C 5 - H 6 /102. RY*( 1) C 10 0.09 1.68 0.011 8. BD ( 1) C 5 - H 6 /104. RY*( 3) C 10 0.34 1.64 0.021 8. BD ( 1) C 5 - H 6 /105. RY*( 4) C 10 0.12 2.08 0.014 8. BD ( 1) C 5 - H 6 /164. RY*( 1) C 18 0.05 1.56 0.008 8. BD ( 1) C 5 - H 6 /194. BD*( 2) C 3 - C 10 1.41 0.57 0.027 9. BD ( 1) C 5 - C 7 / 50. RY*( 3) C 1 0.05 1.53 0.008 9. BD ( 1) C 5 - C 7 / 61. RY*( 3) C 3 0.05 1.53 0.008 9. BD ( 1) C 5 - C 7 / 92. RY*( 1) C 9 0.29 1.85 0.021 9. BD ( 1) C 5 - C 7 / 95. RY*( 4) C 9 0.07 2.24 0.012 9. BD ( 1) C 5 - C 7 /102. RY*( 1) C 10 0.29 1.85 0.021 9. BD ( 1) C 5 - C 7 /105. RY*( 4) C 10 0.07 2.24 0.012 9. BD ( 1) C 5 - C 7 /191. BD*( 2) C 1 - C 9 0.48 0.73 0.018 9. BD ( 1) C 5 - C 7 /194. BD*( 2) C 3 - C 10 0.49 0.73 0.018 10. BD ( 2) C 5 - C 7 / 93. RY*( 2) C 9 0.05 1.05 0.007 10. BD ( 2) C 5 - C 7 / 94. RY*( 3) C 9 0.36 1.36 0.022 10. BD ( 2) C 5 - C 7 / 95. RY*( 4) C 9 0.12 1.79 0.014 10. BD ( 2) C 5 - C 7 / 96. RY*( 5) C 9 0.06 2.31 0.012 10. BD ( 2) C 5 - C 7 / 97. RY*( 6) C 9 0.06 2.16 0.011 10. BD ( 2) C 5 - C 7 / 99. RY*( 8) C 9 0.08 2.26 0.013 10. BD ( 2) C 5 - C 7 /103. RY*( 2) C 10 0.05 1.05 0.007 10. BD ( 2) C 5 - C 7 /104. RY*( 3) C 10 0.36 1.36 0.022 10. BD ( 2) C 5 - C 7 /105. RY*( 4) C 10 0.12 1.79 0.014 10. BD ( 2) C 5 - C 7 /106. RY*( 5) C 10 0.06 2.31 0.012 10. BD ( 2) C 5 - C 7 /107. RY*( 6) C 10 0.06 2.16 0.011 10. BD ( 2) C 5 - C 7 /109. RY*( 8) C 10 0.08 2.26 0.013 10. BD ( 2) C 5 - C 7 /191. BD*( 2) C 1 - C 9 8.99 0.28 0.046 10. BD ( 2) C 5 - C 7 /194. BD*( 2) C 3 - C 10 8.99 0.28 0.046 10. BD ( 2) C 5 - C 7 /202. BD*( 1) C 9 - C 21 0.10 0.66 0.008 10. BD ( 2) C 5 - C 7 /204. BD*( 1) C 10 - C 18 0.10 0.66 0.008 10. BD ( 2) C 5 - C 7 /212. BD*( 1) C 18 - H 20 0.14 0.71 0.010 10. BD ( 2) C 5 - C 7 /215. BD*( 1) C 21 - H 23 0.14 0.71 0.010 11. BD ( 1) C 5 - C 15 / 61. RY*( 3) C 3 0.21 1.49 0.016 11. BD ( 1) C 5 - C 15 /103. RY*( 2) C 10 0.15 1.46 0.013 11. BD ( 1) C 5 - C 15 /104. RY*( 3) C 10 0.34 1.77 0.022 11. BD ( 1) C 5 - C 15 /105. RY*( 4) C 10 0.24 2.21 0.021 11. BD ( 1) C 5 - C 15 /164. RY*( 1) C 18 0.06 1.69 0.009 11. BD ( 1) C 5 - C 15 /165. RY*( 2) C 18 0.13 1.54 0.013 11. BD ( 1) C 5 - C 15 /194. BD*( 2) C 3 - C 10 1.34 0.70 0.029 12. BD ( 1) C 7 - H 8 / 50. RY*( 3) C 1 0.13 1.36 0.012 12. BD ( 1) C 7 - H 8 / 92. RY*( 1) C 9 0.09 1.68 0.011 12. BD ( 1) C 7 - H 8 / 94. RY*( 3) C 9 0.34 1.64 0.021 12. BD ( 1) C 7 - H 8 / 95. RY*( 4) C 9 0.12 2.08 0.014 12. BD ( 1) C 7 - H 8 /176. RY*( 1) C 21 0.05 1.56 0.008 12. BD ( 1) C 7 - H 8 /191. BD*( 2) C 1 - C 9 1.41 0.57 0.027 13. BD ( 1) C 7 - C 14 / 50. RY*( 3) C 1 0.21 1.49 0.016 13. BD ( 1) C 7 - C 14 / 93. RY*( 2) C 9 0.15 1.46 0.013 13. BD ( 1) C 7 - C 14 / 94. RY*( 3) C 9 0.34 1.77 0.022 13. BD ( 1) C 7 - C 14 / 95. RY*( 4) C 9 0.24 2.21 0.021 13. BD ( 1) C 7 - C 14 /176. RY*( 1) C 21 0.06 1.69 0.009 13. BD ( 1) C 7 - C 14 /177. RY*( 2) C 21 0.13 1.54 0.013 13. BD ( 1) C 7 - C 14 /191. BD*( 2) C 1 - C 9 1.34 0.70 0.029 21. BD ( 2) C 14 - O 16 /190. BD*( 1) C 1 - C 9 0.05 0.95 0.006 21. BD ( 2) C 14 - O 16 /214. BD*( 1) C 21 - H 22 0.35 0.85 0.015 23. BD ( 2) C 15 - O 17 /193. BD*( 1) C 3 - C 10 0.05 0.95 0.006 23. BD ( 2) C 15 - O 17 /211. BD*( 1) C 18 - H 19 0.35 0.85 0.015 31. CR ( 1) C 5 /104. RY*( 3) C 10 0.05 11.17 0.021 31. CR ( 1) C 5 /194. BD*( 2) C 3 - C 10 0.35 10.09 0.057 32. CR ( 1) C 7 / 94. RY*( 3) C 9 0.05 11.17 0.021 32. CR ( 1) C 7 /191. BD*( 2) C 1 - C 9 0.35 10.09 0.057 197. BD*( 2) C 5 - C 7 / 94. RY*( 3) C 9 0.09 1.09 0.019 197. BD*( 2) C 5 - C 7 / 95. RY*( 4) C 9 0.06 1.52 0.019 197. BD*( 2) C 5 - C 7 /104. RY*( 3) C 10 0.09 1.09 0.019 197. BD*( 2) C 5 - C 7 /105. RY*( 4) C 10 0.06 1.52 0.019 197. BD*( 2) C 5 - C 7 /191. BD*( 2) C 1 - C 9 93.43 0.01 0.054 197. BD*( 2) C 5 - C 7 /194. BD*( 2) C 3 - C 10 93.46 0.01 0.054 208. BD*( 2) C 14 - O 16 /186. RY*( 1) H 22 0.05 0.72 0.016 208. BD*( 2) C 14 - O 16 /215. BD*( 1) C 21 - H 23 0.06 0.43 0.013 210. BD*( 2) C 15 - O 17 /174. RY*( 1) H 19 0.05 0.72 0.016 210. BD*( 2) C 15 - O 17 /212. BD*( 1) C 18 - H 20 0.06 0.43 0.013
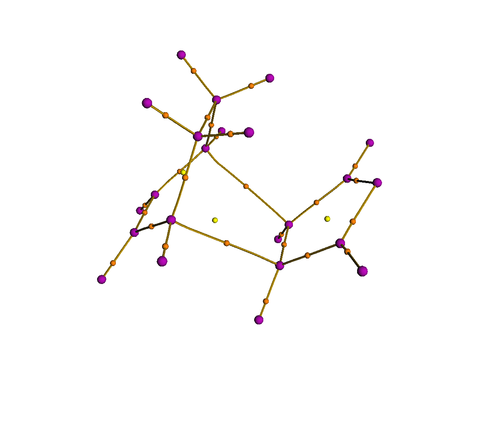
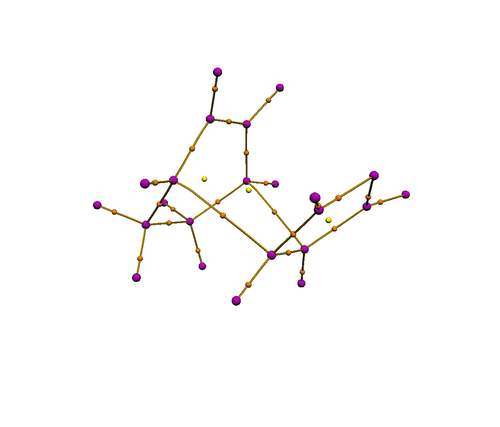
The weakness of the interaction energy predicted by NBO prompted a full topological analysis on the wavefunction of the exo and endo transition states in order to determine nature of the "secondary orbital overlap". Using the Quantum Theory of Atoms in Molecule (QTAIM) method pioneered by Bader et al. [21] QTAIM identifies 4 different critial points, namely bond critical points, ring critical point, nuclear attractors and cage critical points according to the geometric feature of the wavefunction. Bond critical points can be indicator of classical "chemical" bond or "non-covalent" interactions like hydrogen bonds. [22]
QTAIM analysis on the endo and exo isomer showed clearly the nuclear attractors (purple) in positions where the nuclei reside, and bond ciritcal points (orange) in positions where a chemical bond is expected, including the incipient C-C bond. However, no bond critical point is observed between the carbonyl carbon and the diene, indicating the absence of electron accumulation at that region. Therefore, it is unlikely that secondary orbital interactions contribute to any significant extent in the transition state.
| Exo transition state | Endo transition state |
|---|---|
 |
|
Interestingly, ring critical points (yellow) are not only seen in maleic anhydride structure and the cyclohexa-1,3-diene structure, but also in the incipient ring. In the literature, it is reported that the electron density and Laplacian of electron density is directly related to the degree of electron delocalisation and aromaticity of the molecule. [22] In order to investigate the nature of transition state aromaticity, the electronic properties of the three ring critical points are investigated.
| ρ/a.u. | ∇2ρ | |
|---|---|---|
| RCP associated with cyclohexa-1,3-diene | 0.019 | 0.14 |
| RCP associated with maleic anhydride | 0.043 | 0.33 |
| RCP associated with transition state | 0.013 | 0.070 |
| RCP of benzene [22] | 0.020 | 0.163 |
| ρ/a.u. | ∇2ρ | |
|---|---|---|
| RCP associated with cyclohexa-1,3-diene | 0.019 | 0.14 |
| RCP associated with maleic anhydride | 0.043 | 0.33 |
| RCP associated with transition state | 0.014 | 0.072 |
The aromatic character of the transition state is not very significant as judged by the electron density and Laplacian at the ring critical point in comparison with the other RCPs in the system. Comparing with AIM data reported in the literature [22] shows that the electron density and Laplasian of the RCP of the transition state most strongly resemble that of a hydrogen-bonded "quasi-aromatic" ring. This suggests that although the transition state aromatic ring is not as strong as the aromaticity of benzene, the strength of the ring electron delocalisation and aromaticity is not negligible.
Given that electronic factors are not significant in determining endo/exo selectivity, it is possible that steric interaction is responsible. The exo transition state has hydrogen atoms from the cyclohexa-1,3-diene ring pointing up, sterically clashing with the incoming maleic anhydride whilst the endo transition state features maleic anhydride approaching from the more open face of the molecule.
Vibration |
The exo transition state showing the close C---H contact. This contact is absent in the endo transition state.
The rather close C---H contact is not only unfavourable in terms of sterics, but also unfavourable due to like charge repulsion. NBO charge distribution analysis reveals the carbon on carbonyl to be strongly δ+ and the H in close contact with it also δ+. This generates a like-charge repulsion which is absent in the endo transition state as the δ+ proton is not pointing towards the carbonyl carbon.
| Endo TS | 
|
| Exo TS | 
|
Calculation of Activation Energy
The activation energy of the reaction is calculated by taking the difference between transition state electronic and thermal energy and electronic and thermal energy of the reactants. This shows good comparison with experimental data, which is obtained by measuring the variation of rate of reaction with pressure. [23] The deviation from experimental data is likely to be use to solvent effect as the experiment is performed in chloroform whilst the calculations are done in vacuum
| B3LYP/6-31G | B3LYP/6-31G | Experimental Data | |
|---|---|---|---|
| at 0K | at 298.15 K | at 308.15 K | |
| ΔEa(endo) | 17.33 | 17.32 | 11.4 |
| ΔEa(exo) | 19.92 | 19.92 |
Thermodynamic vs. Kinetic Control
In order to investigate the thermodynamic aspect of the reaction. The geometries of the exo and endo products are optimised using B3LYP/6-31G(d) to obtain accurate thermochemical data.
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| exo product (DOI:10042/to-13709 ) | -612.75578539 | -612.569384 | -612.559980 | -612.559036 | -612.604286 |
| endo product(DOI:10042/to-13710 ) | -612.75829022 | -612.572070 | -612.562604 | -612.561660 | -612.607178 |
From the thermochemical data, the endo product is the thermodynamic product (as well as the kinetic product as seen by preceding sections). The equilibrium constant of the reaction converting exo product to endo product can be calculated by the Gibbs equation.
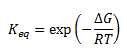
where ΔG is the difference in Gibbs free energy difference between the endo and exo isomer. Substituting and converting to kJ/mol, ΔG=-7.59 kJ/mol and Keq=21.4.
Conclusion
The endo product is both kinetic and thermodynamic product of the reaction. As judged by NBO and AIM analysis, secondary orbital interactions is a relatively minor determinant and it is likely that steric and electrostatic repulsion is the origin of the endo/exo selectivity.
Further Investigation on the Diels-Alder Reaction: On Dimerisation of Cyclopentadiene
Cyclopentadiene dimerises reversibly at room temperature. In order to obtain monomeric cyclopentadiene, it is necessary to "crack" cyclopentadiene dimer by heating. The dimerisation of cyclopentadiene can proceed to form either endo or exo isomer, and experimentally the endo dimer is the kinetic product. [24] This section aims to investigate the mechanism of dimerisation of cyclopentadiene.
The Reactant
Cyclopentadiene is optimised using B3LYP/6-31G(d) in order to extract thermochemical data (DOI:10042/to-13679 ).
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies |
|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | |
| -194.099784410 | -194.008165 | -194.004022 | -194.003078 | -194.034762 |
The Transition State of Diels Alder Reaction
The transition state is optimised by first arranging two cyclopentadiene to a "guessed" transition state. The incipient C-C bond is frozen to 2.2Â and the rest of the structure is optimised to equilibrium using HF/3-21G (exo: DOI:10042/to-13680 , endo: DOI:10042/to-13681 ). The partially optimised structure is then optimised to transition state using HF/3-21G, with derivative of the incipient C-C bonds calculated at every step. The resultant transition structure showed a negative frequency at -651 cm-1 for the endo transition state (DOI:10042/to-13682 ) and -720 cm-1 for the exo transition state (DOI:10042/to-13683 ). Intrinsic reaction coordinate analysis confirms that the transition state links the reactant to the products.
 |
|
 |
|
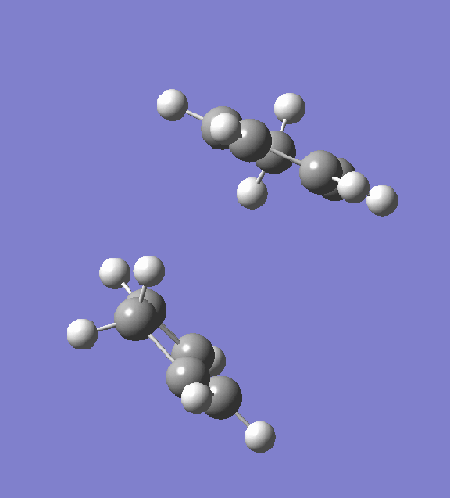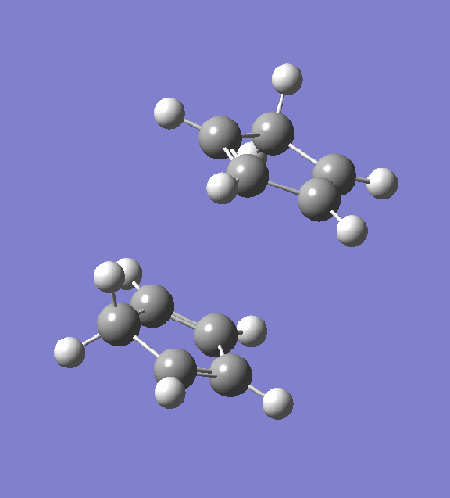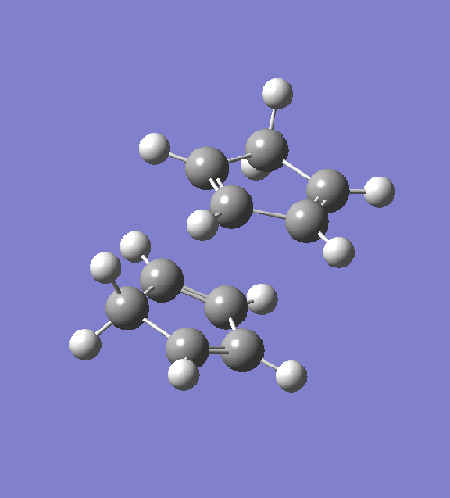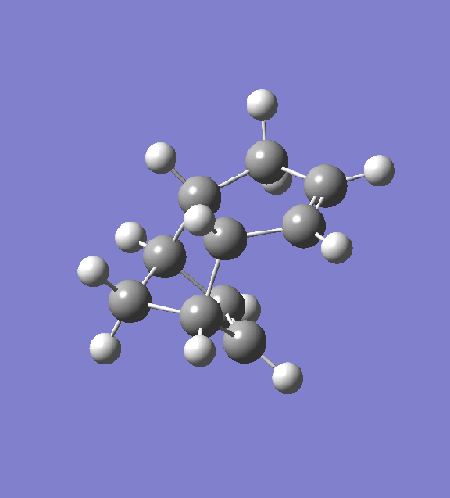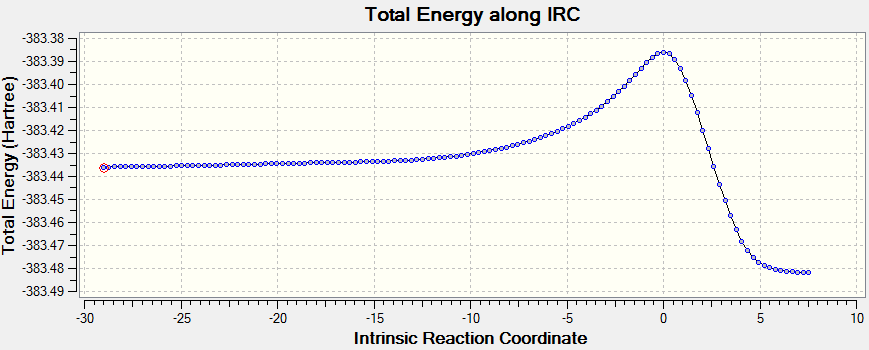
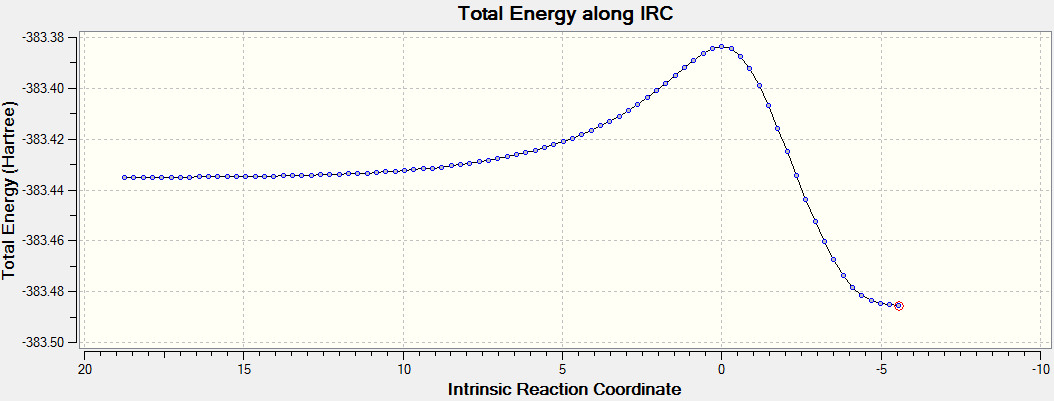
The intrinsic reaction coordinate analysis shows clearly asynchronous bond formation in the endo transition state. However, the formation of the endo product is still a one-step reaction as seen by the presence of only one transition state along the IRC. Reaction through the exo transition state, however, is more synchronous.
The transition state is then re-optimised at B3LYP/6-31G(d) to obtain more accurate thermochemical and structural data.
| Electronic Energy | Sum of Electronic and Zero-Point Energy | Sum of Electronic and Thermal Energies | Sum of Electronic and Thermal Enthalpies | Sum of electronic and thermal Free Energies | |
|---|---|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | at 298.15 K | ||
| exo transition state (DOI:10042/to-13725 ) | -388.16672915 | -387.977872 | -387.969920 | -387.968976 | -388.010293 |
| endo transition state(DOI:10042/to-13726 ) | -388.17124190 | -387.982584 | -387.974540 | -387.973596 | -388.015261 |
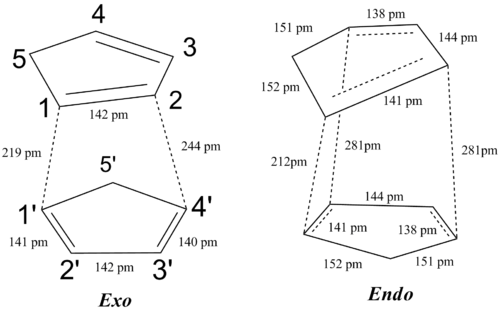
The structure of the both exo and endo transition state showed a degree of asynchronous bond formation, with the endo transition state showing the most dramatic asynchronous character.
In order to validity of the B3LYP/6-31G(d) calculation as so to avoid computational artifacts, MP2/cc-pvdz, a higher level theory and a larger basis set, is used to. the B3LYP/6-31G(d) optimised transition state is reoptimised using MP2/cc-pvdz. The geometric parameter of the endo and exo transition states are analogous to the structures obtained using B3LYP/6-31G(d).
Vibration |
Animation of the exo transition state. DOI:10042/to-13761
Vibration |
Animation of the endo transition state DOI:10042/to-13762
The asynchroneous bond formation can be rationalised in terms of secondary orbital overlap in the transition state. The frontier orbiatals of cyclopentadiene is similar to butadiene, which is shown above.
From looking at the MO diagram of cyclopentadiene, the synergic HOMO-LUMO overlap between cyclopentadiene meant that the bond between C1-C1' is formed by overlap between two "large" lobes whereas the overlap between C2-C4' is between one "large" and one "small" orbitals. As the interaction energy between orbitals are proportional to their overlap integral, the energy of interaction between the "small" and "large" orbital is smaller than energy of interaction between two "large" orbital, hence the bond formation is strongly asynchronous.
In addition, the secondary orbital overlap is in fact of the same nature as one of the incipient C-C bond i.e. the system can choose whether to form the bond between C2-C4' or between C4-C2'. This is also seen in the geometric feature of the transition state. The C2-C4' and C4-C2' distances are both 289 pm. The secondary orbital overlap can also be seen using NBO analysis.
| Acceptor | Donor | Interaction Energy/kcal mol-1 |
|---|---|---|
 |
 |
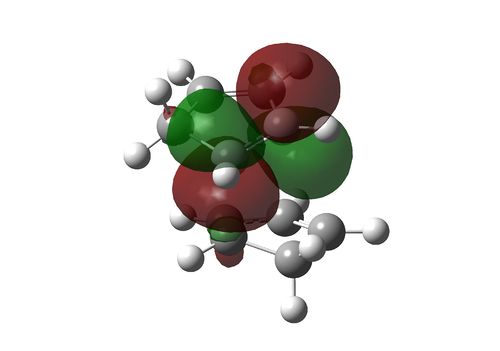44.25 |
|
 |
2.08 |
This clearly shows that the endo transition state is in fact the transition state of two Diels-Alder reactions and is stablised relative to the exo by more orbitals being able to interact in a bonding manner. In fact, the "secondary" orbital interaction in this case is can be a C-C bond forming overlap, and the system can choose between two isomers germinating from the same transition state. Interestingly, the "isomers" are structurally identical and are in fact related by a cope rearrangement.
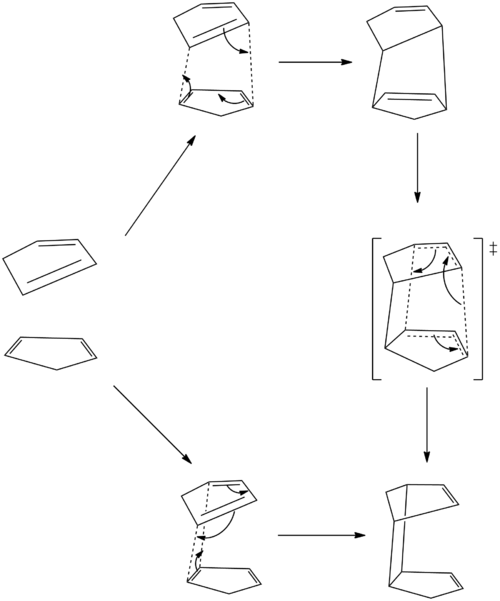
The Transition State of the Associated Cope Rearrangement
The transition state of the associated Cope rearragement was found by the first optimising the "guessed" transition state (DOI:10042/to-13764 ) to equilibrium, holding the forming and breaking C-C bond to 2.2 Â, at HF/3-21 level. The equilibrium geometry is then reoptimized to transition state by HF/3-21G, evaluating numerical second derivative for the two C-C bond associated with the sigmatropic rearrangement (DOI:10042/to-13765 ). Vibrational analysis reveals that a transition state has been reached with negative vibrational frequency of -645 cm-1.
The transition state structure is then further optimised at B3LYP/6-31G(d) level (DOI:10042/to-13766 ).
Vibration |
The transition state of the cope rearrangement is boat-like, as it is constrained by the arrangement of the cyclopentadiene rings. The bond formation and breaking in the transition state is synchronous.
Activation Energy and Kinetics of Dimerisation of Cyclopentadiene
The activation energy is calculated by internal energy of the reactants from that of the transition state and showed reasonable comparison with experimental data. [25]
| B3LYP/6-31G | B3LYP/6-31G | Experimental Data | |
|---|---|---|---|
| at 0K | at 298.15 K | at 298.15 K | |
| ΔEa(endo) | 88.60 | 87.69 | 71.2 |
| ΔEa(exo) | 101.0 | 100.1 |
Conclusion
The transition state of the dimerisation of cyclopentadiene has been elusidated. There is strong secondary orbital overlap to stabilize the endo transition state relative to exo. The strength of the secondary orbital overlap is such that the transition state is able to form two possible Diels-Alder products. The two products are structurally identical and can interconvert between each other via a Cope rearrangement.
References
- ↑ P. Perchukas, "Transition State Theory", Annual Review of Physical Chemsitry, 1981,32, 159, DOI:10.1146/annurev.pc.32.100181.001111
- ↑ D. R. Yarkony, "Diabolical conical intersections", Review of Modern Physics, 1996,68, 985, DOI:10.1103/RevModPhys.68.985
- ↑ M. Klessinger, "Conical Intersections and the Mechanism of Singlet Photoreactions", Angenwante Chemie International Edition, 1995,34, 549, DOI:10.1002/anie.199505491
- ↑ J. K. Wang, Q. Liu, A. H. Zewail, "Solvation Ultrafast Dynamics of Reactions. 9. Femtosecond Studies of Dissociation and Recombination of Iodine in Argon Clusters", Journal of Physical Chemistry, 1995,99, 11309, DOI:10.1021/j100029a004
- ↑ P. A. Rejto, D. Chandler, "Energy Flow during Isomerisation Reactions in Liquids", Journal of Physical Chemistry, 1994,98, 12310, DOI:10.1021/j100098a028
- ↑ P. A. Rejto, E. Blindewald, D. Chandler, "Visualisation of Fast Energy Flow and Solvent Caging in Unimolecular Dynamics", Nature, 1995,375, 129, DOI:10.1038/375129a0
- ↑ 7.0 7.1 C. Doubleday, C. P. Suhrada, K. N. Houk , "Dynamics of the Degenerate Rearrangement of Bicyclo[3.1.0]hex-2-ene", Journal of the American Chemical Society, 2006,128, 90, DOI:10.1021/ja050722w Cite error: Invalid
<ref>tag; name "Itoh2011" defined multiple times with different content - ↑ L. Sun, K. Song, W. Hase, "A SN2 Reaction that Avoids its Deep Potential Energy Minimum", Science, 2005,296, 875, DOI:10.1126/science.1068053
- ↑ A. H. Zewail, "Laser Femtochemistry", Science, 1988,242, 4886
- ↑ A. C. Cope, E. M. Hardy, "The Introduction of Substituted Vinyl Groups. V. A Rearrangement Involving the Migration of an Allyl Group in a Three-Carbon System", Journal of the American Chemical Society, 1940,62, 441, DOI:10.1021/ja01859a055
- ↑ N. Graulich, "The Cope Rearrangement - the first born of a great family", Computational Molecular Science, 2011,1, 172, DOI:10.1002/wcms.17
- ↑ W. v. E. Doering, Y. Wang, "1,3,5-Triphenylhexa-1,5-diene. Chameleonic or Centauric Transition Region?", Journal of the American Chemical Society, 1999,121, 10112, DOI:10.1021/ja9908568
- ↑ J. J. Blavins, D. L. Cooper, P. B. Karadakov, "Aromatic vs Diradical Character in the Transition States of the Cope Rearrangement of 1,5-Hexadiene and Its Cyano Derivatives", Journal of Physical Chemistry. A, 2004,108, 194, DOI:10.1021/ja036660i
- ↑ 14.0 14.1 R. B. Woodward, R. Hoffmann, "Stereochemistry of Electrocyclic Reactions", Journal of the American Chemical Society, 1965,87, 395, DOI:10.1021/ja01080a054 Cite error: Invalid
<ref>tag; name "Woodward.1965" defined multiple times with different content - ↑ H. E. Zimmerman, "On Molecular Orbital Correlation Diagrams, the Occurrence of Möbius Systems in Cyclization Reactions, and Factors Controlling Ground- and Excited-State Reactions. I", Journal of the American Chemical Society, 1966,88, 1564, DOI:10.1021/ja00959a052
- ↑ H. E. Zimmerman, "On Molecular Orbital Correlation Diagrams, the Occurrence of Möbius Systems in Cyclization Reactions, and Factors Controlling Ground- and Excited-State Reactions. II", Journal of the American Chemical Society, 1966,88, 1566, DOI:10.1021/ja00959a053
- ↑ I. Fleming, "Molecular Orbitals and Organic Chemical Reactions", Reference Edition,John Wiley and Sons, 2010
- ↑ D. R. Lide Jr., "A survey of carbon-carbon bond lengths", Tetrahedron, 1962,17, 125, DOI:10.1016/S0040-4020(01)99012-X
- ↑ A. Bondi, "van der Waals Volumes and Radii", Journal of Physical Chemistry, 1964,68, 441, DOI:10.1021/j100785a001
- ↑ H.B. Burgi, J.D. Dunitz, J.M. Lehn, G. Wipff, "Stereochemistry of reaction paths at carbonyl centres", Tetrahedron, 1974,12, 1563, DOI:10.1016/S0040-4020(01)90678-7
- ↑ R. Bader, "A quantum theory of molecular structure and its applications", Chemical Reviews, 1991,91, 893, DOI:10.1021/cr00005a013
- ↑ 22.0 22.1 22.2 22.3 R. Parthasarathi, V. Subramanian, N. Sathyamurthy, "Hydrogen Bonding without Borders: An Atoms-in-Molecules Perspective", Journal of Physical Chemistry A, 2006,110, 3349, DOI:10.1021/jp060571z Cite error: Invalid
<ref>tag; name "Parthasarathi.2006" defined multiple times with different content - ↑ C. A. Eckert, R. A. Grieger, "Mechanistic evidence for the Diels-Alder reaction from high-pressure kinetics, 1970,92, 7149, DOI:10.1021/ja00727a021
- ↑ A. G. Turnbull, H. S, Hull , "A thermodynamic study of the dimerization of cyclopentadiene, 1968,21, 1789, DOI: 10.1071/CH9681789
- ↑ B. Raistrick, R. H. Sapiro, D. M. Newitt, "Liquid-phase reactions at high pressures. Part V. The polymerisation of cyclopentadiene and α-dicyclopentadiene", Journal of the Chemical Society, 1939, 1761