Rep:Mod:aal109 inorg
Module 2: Computational Inorganic Chemistry
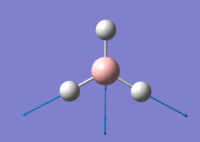
Analysis of BH3
The structure and MO of BH3 is analyzed using density functional theory, with the Becke 3 parameter, Lee-Yang-Parr hybrid exchange-correlation functional B3LYP [1] and the Pople split valance basis set 3-21(g). The basis incorporates 3 primitive Gaussian functions for each core orbital, and the valance orbital is composed of 2 basis function each, with 1 basis function comprising of 1 Gaussian function and 1 basis function comprising of 2 Gaussian functions. The B3LYP hybrid exchange-correlation functional effectively interpolates between energy obtained using Hatree-Fock theory and energy obtained using local density approximation (LDA) and generalised gradient expansion (GGA) density functional. The aim of hybrid density functional is to incorporate the exact treatment of electron exchange (via the Slater determinant) in the Hatree-Fock theory into DFT calculations. Formally,
ExcB3LYP = ExcLDA + a0 (ExLDA-ExHF) + a1 (ExLDA-ExGGA) + a2 (EcLDA-EcGGA)
where Exc is the total energy taking into account of electron exchange and correlation, Ex is electron exchange energy and Ec is electron correlation energy. a0, a1 and a2 are three fitting parameters which are parametrized by comparing with experimental atomization energies, ionization potentials, proton affinities, and total atomic energies. [2]
Geometry Optimisation
The geometry of BH3 is optimised using Gaussian 09 with the Berny algorithm. Equilibrium geometry was obtained after 4 iterations.
Item Value Threshold Converged? Maximum Force 0.000413 0.000450 YES RMS Force 0.000271 0.000300 YES Maximum Displacement 0.001610 0.001800 YES RMS Displacement 0.001054 0.001200 YES
The low frequency vibrations are -66.7625, -66.3592, -66.3589, -0.0020 and 0.0031. The relatively large negative values is an artifact of the low level of theory used. In fact, using the larger basis set 6-31G (d,p) produces -0.9004, -0.7267, -0.0054, 6.8087, 12.2888 and 12.3217 as low energy vibration modes.
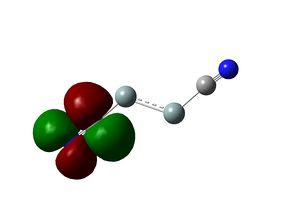
The optimised geometry of BH3 shows trigonal planar geometry with B-H bond length of 1.19 Å and H-B-H bond angle of 120o. Although BH3 does not exist as it readily dimerises to form the celebrated 3c-2e bonded dimer, the B-H bond length agreed closely with reported median terminal B-H bond length of 1.185Á. [3] The bond angle agreed with that expected from VSEPR theory.
Endo Product |
MO Analysis
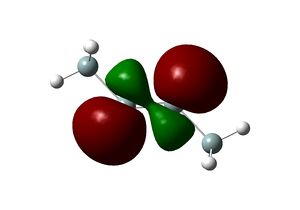
Molecular orbitals of the molecule calculated using B3LYP/3-21(g) strangely not respect the D3h symmetry of the molecule. However, calculation using the larger basis set 6-31G (d,p) produces MOs that are congruent with the molecular symmetry. The shapes and relative energies of the calculated MOs are in agreement with qualitative MO diagram. The LUMO of the molecule is a p orbital on B orthogonal to the molecular plane, which rationalises the Lewis acidity of BH3.
Analysis of Vibrational Modes
There are 3N-6=6 distinct modes of molecular vibrations for BH3.
| Symmetry in D3h point group | Frequency calculated using B3LYP/6-31G(d,p) | Intensity | Frequency calculated using B3LYP/3-21 | Intensity | Form of the Vibration |
|---|---|---|---|---|---|
| Symmetric A2 | 1163 | 93 | 1144 | 93 |  |
| Doubly degenerate, antisymmetric E' | 1213 | 14 | 1204 | 12 |  |
| Doubly degenerate, antisymmetric E' | 1213 | 14 | 1204 | 12 |  |
| Totally symmetric A1' | 2852 | 0 | 2598 | 12 |  |
| Doubly degenerate, antisymmetric E' | 2715 | 126 | 2737 | 104 |  |
| Doubly degenerate, antisymmetric E' | 2715 | 126 | 2737 | 104 |  |
It is noteworthy that the frequency and intensity obtained by B3LYP/6-31G(d,p) and B3LYP/3-21 are slightly different. It is likely that the larger basis set 6-31G(d,p) will yield a more accurate answer as it takes into account higher energy valance orbitals on B and H. The totally symmetric A1' mode has zero intensity as it does not involve a change in dipole moment.
Analysis of Natural Bonding Orbitals
Natural bonding orbital is a class of localised molecular orbitals which is designed to match the valance-bond intuition of a chemical bond rather than formally delocalised canonical molecular orbitals. Localised molecular orbitals are unitary transformation of the canonical molecular orbital. Formally, the NBO algorithm performs unitary transformations such that atomic orbitals are transformed into "natural" atomic orbitals (NAO), NAOs are then "mixed" into hybrids orbitals and hybrids orbitals are linearly combined to form bonding and anti-bonding orbitals.
Atomic orbital → NAO → NHO → NBO
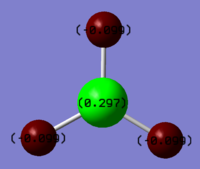
The NBO population analysis showed that the central boron is formally +0.297 whilst the three hydrogen atoms are formally -0.099, suggesting hydridic rather than protic nature of the hydrogen atoms attached to BH3. The NBO analysis also reveals that the B-H bond formally comprise of a sp2 hybrid orbital on boron bonding with a s atomic orbital on H.
Second order perturbation theory analysis showed no significant interaction between donor and acceptor NBO. This is expected as the simple molecule does not have any important stereo-electronic interaction.
Log Files
Optimisation of BH3 using B3LYP/3-21(G): https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Aal109_borane.log
Vibrational analysis and NBO analysis of BH3 using B3LYP/3-21(G): https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Aal109_borane_freq_mo.log
Geometry optimisation, vibrational analysis and NBO analysis of BH3 using B3LYP/6-31G(d,p): https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Aal109_borane_freq_mo_6_31_g.log
Analysis of ThBr3
Thallium (III) bromide is an unstable, highly toxic compound which decomposes to thallium (II) bromide above 40oC. [4] Due to large number of electron present in thalium, a pseudopotential is used to avoid explicit calculation of core electrons. The pseudopotential is an effective potential constructed such that core states are eliminated and the valence electrons are described by nodeless pseudo-wavefunctions. In this approach only the valence electrons are dealt with explicitly, while the core electrons are being considered together with the nuclei as rigid non-polarizable ion cores. Mathematically, the oscillatory behavior of the wavefunction near to nucleus is smoothed, but the effective wavefunction still matches the actual wavefunction beyond a certain cutoff radius.
The optimised structure of ThBr3 is calculated using DFT, with the Los Alamos pseudopotential LanL2DZ and exchange-correlation functional B3LYP. The geometry of ThBr3 is restricted at D3h to speed up the computation. Convergence is met after 3 iterations.
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000022 0.001800 YES RMS Displacement 0.000014 0.001200 YES
| ThBr3 | ||
|---|---|---|
| File Name | THALIUM_BROMIDE | |
| File Type | .log | |
| Calculation Type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | LANL2DZ | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -91.21812851 | a.u. |
| RMS Gradient Norm | 0.0000009 | a.u. |
| Imaginary Freq | ||
| Dipole Moment | 0 | Debye |
| Point Group | D3H |
In the optimized structure, the bond length of the Th-Br bond is 2.65 Å and the Br-Th-Br bond angle is 120.0o. This is in agreement with the X-ray structure of the tetrahydrate, which has a Th-Br bond length of 2.52 Å and Br-Th-Br angles of 122.3o and 118.6o. [4] The slight deviation of the calculated values from crystal structure is likely to be due to crystal packing forces.
Endo Product |
Using the equilibrium geometry, frequencies of vibrations are calculated using the same level of theory. It is crucial that the same level of theory in used in both geometry optimisation and frequency calculation as the harmonic approximation and the theory of normal modes only holds when the system is displaced infinitesimally away from the equilibrium geometry, i.e. the first derivative of the energy with respect to displacement of atoms equals 0. If another theory is used for vibration analysis, the computed equilibrium geometry is no longer the equilibrium geometry at that level and hence and frequencies computed are meaningless.
The low frequency modes, corresponding to rotation and translational degrees of freedom, are as follows:
Low frequencies --- -2.7110 0.0000 0.0000 0.0000 1.1507 4.1778
The fact that the low frequency modes are close to zero indicates success of the optimization. The "real" modes are 46, 47, 52, 165.2386, 210.6288 and 210.7006. The fact that they are all positive shows that the structure is a stable one residing in an energy well rather than an energy maxima, which would have imaginary frequencies.
In some structures, Gaussview does not draw a chemical bond in places that one might expect a bond. That is because Gaussview uses a simple distance criterion for establishing whether a chemical bond exist. In reality, a covalent bond is a region of electron density in between 2 atoms. In fact, the Atom-in-Molecule formalism provides a much better criterion for a chemical bond. According to Bader, [5] a "bond critical point" is a point where electron density falls down in two perpendicular directions of space and rises in the third direction, i.e a saddle point of electron density with a maximum of electron density in 2 directions of space and a minimum in the third one.
Log Files
Geometry optimisation of ThBr3: https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Aal109_THALIUM_BROMIDE.LOG
Frequency analysis of ThBr3: https://wiki.ch.ic.ac.uk/wiki/index.php?title=File:Aal109_THALIUM_BROMIDE_VIBRATIONS.LOG
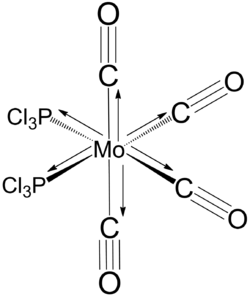
cis and trans [Mo(PCl3)2(CO)4]
cis isomer
Geometry optimisation
The geometry of the complex is first optimised at B3LYP/LANL2MB level. The relatively small basis set meant that an accurate geometry cannot be obtained. However, this initial optimisation would provide reasonable starting structures for further optimisation at higher level of theory. In order to account for the low level of theory, the convergence criteria is lowered to maximum step size of 0.01 au and an RMS force of 0.0017 au (the Gaussian keyword "opt=loose").
Geometry optimisation of the cis isomer converged after 12 iterations.
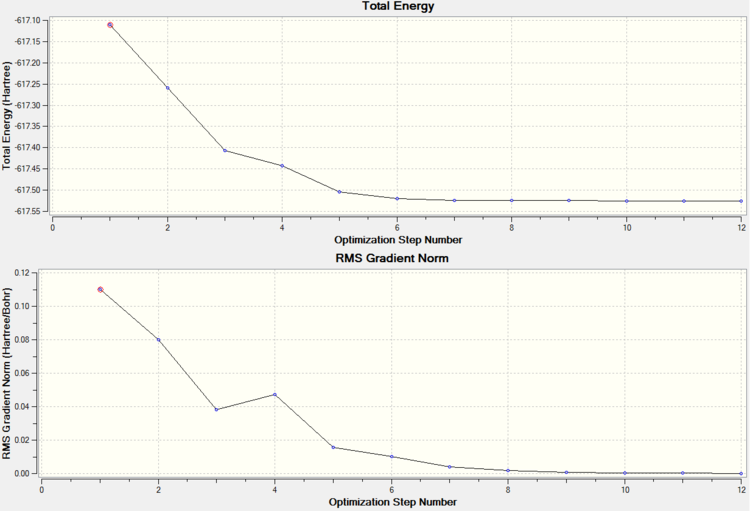
| Bond length/Å | |
|---|---|
| Mo-P | 2.53 |
| axial Mo-C | 2.11 |
| equatorial Mo-C | 2.06 |
| axial C-O | 1.19 |
| equatorial C-O | 1.19 |
| P-Cl | 2.41 |
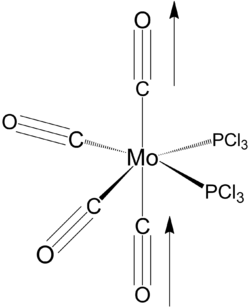
It is noteworthy that the the optimised dihedral angle of Cl-P-Mo-C(axial) is 29o. In order to obtain a lower energy equilibrium structure, the Cl-P-Mo-C(axial) is adjusted to 0, and the adjacent PCl3 groups are such that one Cl points up parallel to the axial bond, and that one Cl of the other group points down. This modified structure is than optimised using B3LYP/LANL2DZ, with stricter convergence criteria ("int=ultrafine scf=conver=9").
Endo Product |
Equilibrium geometry of cis[Mo(PCl3)2(CO)4] obtained using B3LYP/LANL2DZ
| Bond length/Å | |
|---|---|
| Mo-P | 2.51 |
| axial Mo-C | 2.05 |
| equatorial Mo-C | 2.01 |
| axial C-O | 1.17 |
| equatorial C-O | 1.18 |
| P-Cl | 2.24 |
However, as 3d orbital is phosphorous is relatively accessible, neglecting the d orbitals as in LANL2DZ may lead to inaccuracies. Therefore, d function is added to the phosphorus atom by putting to keyword "extrabasis" in the route section of the input file and
(blank line) P 0 D 1 1.0 0.55 0.100D+01 **** (blank line)
at the end of the input file. The resulting geometry reveals significantly shorter P-Cl bond. This is likely to be due to significant degree of valance d-orbital participation in the P-Mo and P-Cl bond, thus removing the d-orbital leads to effectively a weaker bond. The optimised geometry compares well with experimental X-ray structure obtained for cis-[Mo(PPh3)2(CO)4]. [6]
| Bond length (calculated)/Å | Experiential bond length | |
|---|---|---|
| Mo-P | 2.48 | 2.58 |
| axial Mo-C | 2.05 | 2.02 |
| equatorial Mo-C | 2.02 | 1.97 |
| axial C-O | 1.17 | 1.17 |
| equatorial C-O | 1.18 | 1.14 |
| P-Cl | 2.11 | -- |
Endo Product |
Equilibrium geometry of cis[Mo(PCl3)2(CO)4] obtained using B3LYP/LANL2DZ with extra d AO function for P
Vibrational Analysis
Vibrational analysis is done on the equilibrium structure obtained using B3LYP/LANL2DZ, and structure obtained using B3LYP/LANL2DZ with extra d AO function on P. The fact that the low frequency modes, corresponding to translation and rotation degrees of freedom, are close to zero suggest that the geometry optimization is successful.
| B3LYP/LANL2DZ | -1.7808, 0.0005, 0.0006, 0.0006, 1.0186, 1.4977 |
| B3LYP/LANL2DZ with d AO basis on P | -1.2643, -0.0008, -0.0007, -0.0007, 0.8166, 1.9570 |
The vibrational modes are all positive for the optimised structure with or without d orbital function on P, confirming that a stable geometry is obatined.
| Frequency (without addition d AO function on P) | Intensity | Frequency (with addition d AO function on P) | Intensity | Notes |
|---|---|---|---|---|
| 11 | 0.03 | 12 | 0.02 | |
| 18 | 0.007 | 20 | 0.004 | |
| 42 | 0.005 | 46 | 0.0008 | |
| 44 | 0.1 | 50 | 0.03 | |
| 56 | 0.8 | 63 | 0.5 | |
| 67 | 0.2 | 71 | 0.2 | |
| 78 | 0.2 | 80 | 0.3 | |
| 81 | 0.5 | 85 | 0.7 | |
| 86 | 0.02 | 86 | 0.04 | |
| 93 | 0.4 | 93 | 0.5 | |
| 98 | 0.07 | 98 | 0.4 | |
| 98 | 0.3 | 111 | 0.07 | |
| 99 | 0.006 | 116 | 0.02 | |
| 105 | 0.009 | 122 | 0.05 | |
| 121 | 0.5 | 139 | 0.5 | |
| 139 | 0.7 | 160 | 0.1 | |
| 144 | 1 | 166 | 0.2 | |
| 165 | 0.0004 | 196 | 0.1 | |
| 170 | 0.07 | 198 | 0.0006 | |
| 176 | 0.7 | 204 | 0.3 | |
| 177 | 0.002 | 207 | 0.0259 | |
| 235 | 13 | 269 | 30 | |
| 236 | 29 | 270 | 14 | |
| 378 | 12 | 382 | 12 | |
| 379 | 0.006 | 385 | 0.005 | |
| 396 | 14 | 408 | 0.1 | |
| 396 | 9 | 409 | 9 | |
| 405 | 2 | 413 | 59 | |
| 408 | 274 | 422 | 3 | |
| 410 | 8 | 425 | 52 | |
| 419 | 2 | 443 | 335 | P-Mo group antisymmetric stretch  |
| 425 | 77 | 450 | 2 | |
| 432 | 241 | 457 | 86 | |
| 437 | 153 | 466 | 178 | P-Mo bending  |
| 459 | 46 | 477 | 87 | |
| 465 | 38 | 483 | 250 | ligand "breathing" mode  |
| 514 | 0.02 | 512 | 0.04 | |
| 530 | 0.3 | 529 | 0.04 | |
| 564 | 82 | 567 | 114 | Mo-C bending  |
| 580 | 93 | 586 | 109 | Mo-C bending  |
| 598 | 105 | 600 | 113 | Mo-C bending  |
| 1945 | 763 | 1938 | 1604 | carbonyl group stretching (see below) |
| 1949 | 1498 | 1941 | 813 | |
| 1958 | 633 | 1952 | 588 | |
| 2023 | 598 | 2019 | 545 |
 |
| Predicted IR spectrum without d AO basis on P |
 |
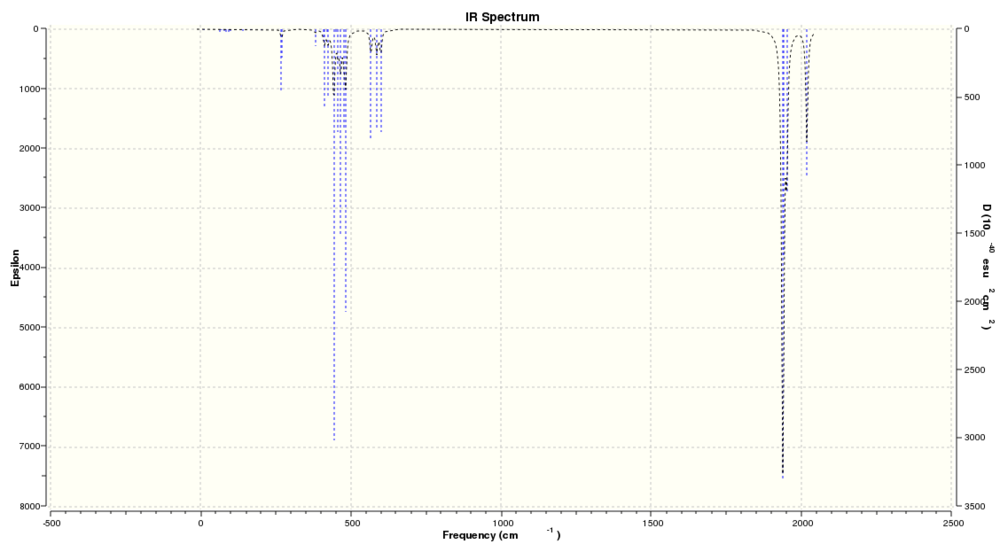| Predicted IR spectrum with d AO basis on P |
The lowest frequency mode correspond to rotation of the -PCl3 groups. The low frequency suggests a very low barrier to rotation and the low intensity shows that there are very little change in the dipole moment brought about by rotation of the ligand. The higher energy modes corresponds to the collective bending of Mo-P and Mo-C bond, and the 4 bands above 1900 cm-1 corresponds to carbonyl group stretch. As the frequency of vibration is inversely proportional proportional to reduced mass, vibrations that involves the very heavy molybdenum centre will occur at very low frequency. At room temperature, low frequency vibrational modes will be excited as kBT=208cm-1 at 300K.
The complex has approximate C2V symmetry. As such, the reducible representation of the group is
| C2V | E | C2 | σv(xz) | σv(yz) |
| χ per unshifted vibration | 4 | 2 | 2 | 2 |
Using the reduction formula, the irreducible representation is
Γ = 2 A1 + B1 + B2
Using the character table for C2V, all 4 modes are IR active, and have the same symmetry as the z, x, and y axis respectively. As the compound cis-[Mo(CO)4(Pcl3)2]) is not reported in the literature, comparison with the corresponding complex with triphenoxidephosphine ligand was made as chloro and phenoxide are both electron donating groups. The predicted vibration frequency agrees broadly with literature data for cis-[Mo(CO)4(PPh3)2] measured in a tetrachloroethylene solution [7]. The difference in the stretching frequency is likely to be due to the difference in the ligand, which directly translate to ligand stretching frequency through affects in the strength of back-π donation from Mo to CO.
| Frequency (without d AO on P) | Frequency (with d AO on P) | Literature data for cis-[Mo(CO)4(PPh3)2] | Symmetry | Form of Vibration |
|---|---|---|---|---|
| 1945 | 1938 | 1941 | B2 |  |
| 1958 | 1952 | 1947 | B1 |  |
| 1949 | 1941 | 1964 | A1 |  |
| 2023 | 2019 | 2049 | A1 |  |
trans isomer
Geometry Optimisation
The geometry of the complex is first optimised using at B3LYP/LANL2MB level with loose convergence criteria (keyword "opt=loose").
| Bond length/Å | |
|---|---|
| Mo-P | 2.48 |
| Mo-C | 2.11 |
| C-O | 1.19 |
| P-Cl | 2.40 |
The optimised geometry showed the two -PCl3 in a staggering conformation. The structure is then further optimised using B3LYP/LANL2DZ, with stricter convergence criteria ("int=ultrafine scf=conver=9"). In order to obtain a lower energy equilibrium structure, the structure is adjusted such that the PCl3 groups are eclipsed and that one Cl of each group lies parallel to one Mo-C bond.
| Bond length/Å | |
|---|---|
| Mo-P | 2.44 |
| Mo-C | 2.06 |
| C-O | 1.17 |
| P-Cl | 2.24 |
Endo Product |
Equilibrium geometry of trans[Mo(PCl3)2(CO)4] obtained using B3LYP/LANL2DZ
As with the optimisation of the cis isomer, the structure is reoptimised with B3LYP/LANL2DZ with addition of d AO functions on P. The resulting geometry reveals significantly shorter P-Cl bond. The bond lengths in the optimised geometry compares well with the x-ray structure of trans-[Mo(PPh3)2(CO)4] co-crystallised with 1,4-bis (diphenylphosphino)-2,5-difluorobenzene. [8]
| Calculated Bond length/Å | Measured Bond length/Å | |
|---|---|---|
| Mo-P | 2.42 | 2.50 |
| Mo-C | 2.06 | 2.01 |
| C-O | 1.17 | 1.17 |
| P-Cl | 2.12 | -- |
Endo Product |
Equilibrium geometry of trans[Mo(PCl3)2(CO)4] obtained using B3LYP/LANL2DZ
Vibrational Analysis
As in the analysis of the cis isomer, vibrational analysis is done on the equilibrium structure obtained using B3LYP/LANL2DZ, and structure obtained using B3LYP/LANL2DZ with extra d AO function on P. The fact that the low frequency modes, corresponding to translation and rotation degrees of freedom, are close to zero suggest that the geometry optimization is successful.
| B3LYP/LANL2DZ | -2.2123, -1.5998, -0.0003, -0.0003, -0.0001, 3.0997 |
| B3LYP/LANL2DZ with d AO basis on P | -2.3020, -1.9665, -0.0006, -0.0005, 0.0003, 2.8691 |
The vibrational frequencies of the optimized structure are all positive, suggesting a stable equilibrium structure.
| Frequency (without addition d AO function on P) | Intensity | Frequency (with addition d AO function on P) | Intensity | Notes |
|---|---|---|---|---|
| 5 | 0.0003 | 4 | 0.05 | |
| 6 | 0.0008 | 7 | 0 | |
| 37 | 0.02 | 40 | 0.1 | |
| 40 | 0.3 | 44 | 0.06 | |
| 72 | 0.0001 | 74 | 0.004 | |
| 79 | 1 | 80 | 1 | |
| 79 | 0 | 82 | 1 | |
| 80 | 1 | 84 | 0.01 | |
| 83 | 0.001 | 85 | 0.0001 | |
| 88 | 0.002 | 88 | 0.007 | |
| 97 | 0.03 | 98 | 0.2 | |
| 102 | 0 | 117 | 0.0002 | |
| 103 | 0 | 117 | 0 | |
| 110 | 0.009 | 124 | 0.009 | |
| 123 | 0.4 | 146 | 0.5 | |
| 125 | 0.4 | 148 | 0.4 | |
| 161 | 0 | 193 | 0.001 | |
| 163 | 0.06 | 193 | 0.6 | |
| 172 | 6 | 196 | 0.4 | |
| 190 | 0.8 | 217 | 0.2 | |
| 191 | 0.8 | 218 | 0.2 | |
| 240 | 0.04 | 273 | 50 | |
| 252 | 38 | 276 | 0.04 | |
| 346 | 0.004 | 347 | 0.01 | |
| 389 | 0.02 | 398 | 0.7 | |
| 389 | 2 | 401 | 4 | |
| 389 | 0.4 | 404 | 0.09 | |
| 390 | 2 | 404 | 0.0001 | |
| 401 | 4 | 407 | 5 | |
| 407 | 0.04 | 411 | 0.03 | |
| 409 | 728 | 435 | 801 | Mo-P asymmetric stretch  |
| 423 | 168 | 454 | 200 | Mo-P in plane bend |
| 426 | 166 | 455 | 201 | Mo-P out of plane bend |
| 436 | 0.1 | 461 | 0.01 | |
| 436 | 6 | 462 | 10 | |
| 458 | 0 | 485 | 0.1 | |
| 483 | 0.002 | 489 | 0.3 | |
| 523 | 0.01 | 528 | 0.002 | |
| 574 | 88 | 578 | 111 | degenerate out-of-plane Mo-C bending  |
| 574 | 90 | 578 | 113 | degenerate out-of-plane Mo-C bending |
| 604 | 138 | 610 | 128 | Mo-C bending  |
| 1950 | 1475 | 1939 | 1606 | carbonyl group stretches (see below) |
| 1951 | 1467 | 1940 | 1606 | |
| 1977 | 0.6 | 1967 | 6 | |
| 2031 | 4 | 2026 | 5 |
 |
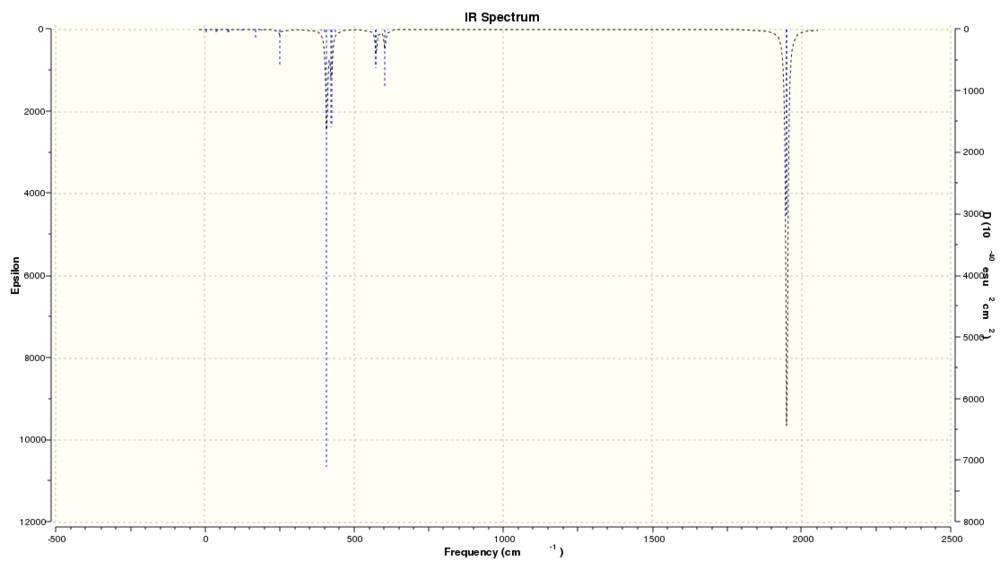| Predicted IR spectrum without d AO basis on P |
 |
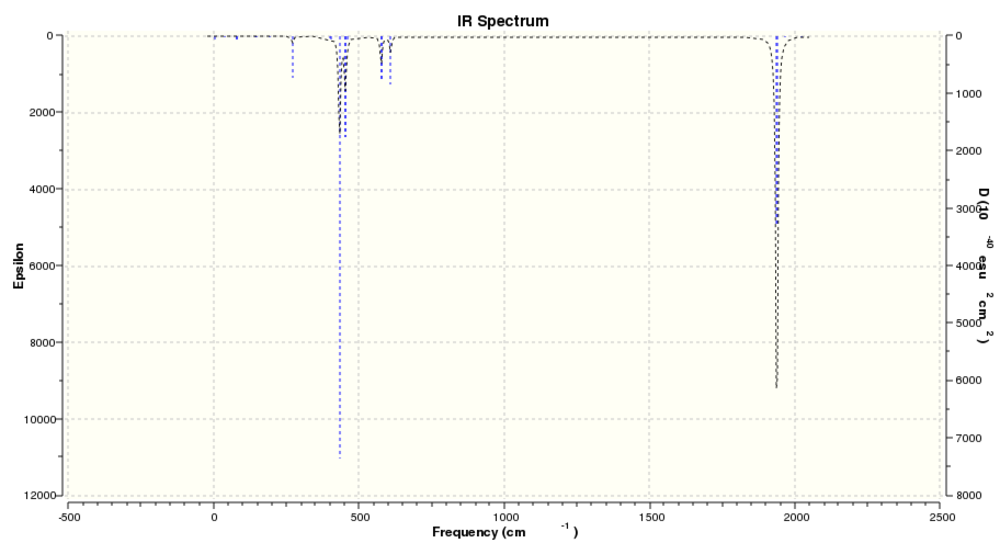| Predicted IR spectrum with d AO basis on P |
The complex has approximate D4h symmetry and working out the reducible representation
| D4h | E | 2 C4 | C2 | 2C2' | 2C2 | i | 2S4 | σh | 2σv | 2σd |
| χ per unshifted vibration | 4 | 0 | 0 | 2 | 2 | 0 | 0 | 4 | 2 | 0 |
Using the reduction formula, the irreducible representation is
Γ = 2 A1g + B1g + Eu
Using the character table for D4h, only the 2 degenerate Eu modes are IR active. The A1g and B1g modes does not have incur a change in dipole moment, and hence are IR inactive. However, the complex is only approximately D4h, as distortions such as the conformation of the PCl3 ligand reduces the overall molecular symmetry. Hence in reality, the A1g and B1g modes have low but non-vanishing intensity, as seen in the table above. As the complex trans-[Mo(CO)4(PCl3)2] is not available in the literature, comparison with the corresponding complex with triphenoxidephosphine ligand was made as chloro and phenoxide are both electron donating groups. The resulting data compares well with literature data for the complex trans-[Mo(CO)4(P(OPh)3)2] measured in saturated hydrocarbon [9].
| Frequency (without d AO on P) | Frequency (with d AO on P) | Symmetry | Literature data for trans-[Mo(CO)4(P(OPh)3)2] | Form of Vibration |
|---|---|---|---|---|
| 1950 | 1939 | 1943 | Eu | degenerate carbonyl asymmetric stretch |
| 1951 | 1940 | 1943 | Eu | |
| 1977 | 1967 | 1985 | B1g |  |
| 2031 | 2026 | 2054 | A1g |  |
Relative energy of cis and trans isomer
The relative energy of the cis and trans isomer depends on the subtle balance between sterics and electronics. Bulky phosphine ligand prefers to be trans to each other to minimise steric clash. However, the strong π-aceptor nature of the carbonyl group meant that electron donating ligand trans to the carbonyl group is preferred over carbonyl group being trans to each other.
| B3LYP/LANL2DZ (hatree) | B3LYP/LANL2DZ (kJ/mol) | B3LYP/LANL2DZ with d AO function on P (hatree) | B3LYP/LANL2DZ with d AO function on P(kJ/mol) | |
|---|---|---|---|---|
| cis isomer | -623.57707195 | -1637200 | -623.69291202 | -1637506 |
| trans isomer | -623.57603103 | -1637199 | -623.69415608 | -1637508 |
The above table showed that the cis and trans isomers are very close in energy, with the two different methods reporting contradictory results. Using the energies obtained using B3LYP/LANL2DZ with d AO function on P, the equilibrium constant of
cis-[Mo(PCl3)2(CO)4] <---> trans-[Mo(PCl3)2(CO)4]
can be calculated using the Boltzmann formula
Keq=exp(-ΔG/kT)
with ΔG taken as the difference in energy of the two isomers. Substituting values for ΔG, the equilibrium constant at 300K is Keq=1.0013. Exploring the effect of electronic effect, the energies if the cis and trans complex is compared for ligands PBr3, PCl3 and PF3, which is of deceasing strength in σ bond to metal due to the effect of electronegative substituent making the lone pair on P lower in energy thus less avaliable for bonding with metal. This should render the trans form more favourable as in the absence of sterics, electronic factor should dominate. However, the steric bulk of the ligand also decreasing in the order PBr3< PCl3 < PF3 and thus it is unclear whether steric effect or electronic effect would be the dominant factor.
| Energy of cis isomer/Hatree | Energy of trans isomer/Hatree | Etrans-Ecis/ kJmol-1 (3 s.f) | Keq | |
|---|---|---|---|---|
| PF3 | -1133.27938535 | -1133.27993366 | -1.44 | 1.78 |
| PCl3 | -623.69291202 | -623.694156088 | -3.27 | 3.71 |
| PBr3 | -612.98384036 | -612.98549647 | -4.35 | 5.72 |
From the above table, the steric effect seems to be dominant, with more bulky phosphine ligad favouring trans the most. Exploring whether the equilibrium can be engineered to favour the cis isomer,[Mo(0H3)2(CO)4] is subsequently modeled. Water is much smaller than the phosphine ligand despite that fact that the σ donor donating nature of water is far less than phosphine as oxygen is much more electronegative.
| Energy of cis isomer/Hatree | Energy of trans isomer/Hatree | Etrans-Ecis/ kJmol-1 (3 s.f) | Keq |
|---|---|---|---|
| -673.77513232 | -673.74183694 | 87.4 | 0 |
In the case of water as ligand, the equilibrium is completely reversed, with the cis isomer favoured very strongly over trans.
Logfiles
Optimised Geometry (B3LYP/LANL2DZ) of the cis-[Mo(PCl3)2(CO)4]: DOI:10042/to-13158
Optimised Geometry (B3LYP/LANL2DZ) of the trans-[Mo(PCl3)2(CO)4]: DOI:10042/to-13159
Frequency Analysis (B3LYP/LANL2DZ) of the cis-[Mo(PCl3)2(CO)4]: DOI:10042/to-13160
Frequency Analysis (B3LYP/LANL2DZ) of the trans-[Mo(PCl3)2(CO)4]: DOI:10042/to-13161
Optimised Geometry and frequency analysis (B3LYP/LANL2DZ with d orbital on P) of the cis-[Mo(PCl3)2 (CO)4]: DOI:10042/to-13162
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ with d orbital on P) of the trans-[Mo(PCl3)2 (CO)4]: DOI:10042/to-13159
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ with d orbital on P) of the cis-[Mo(PBr3)2(CO)4]: DOI:10042/to-13164
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ with d orbital on P) of the cis-[Mo(PF3)2(CO)4]: DOI:10042/to-13165
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ with d orbital on P) of the trans-[Mo(PBr3)2(CO)4]: DOI:10042/to-13166
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ with d orbital on P) of the trans-[Mo(PBr3)2(CO)4]: DOI:10042/to-13166
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ for Mo and B3LYP/6-311G for other elements) of the trans-[Mo(OH2)2(CO)4]: DOI:10042/to-13193
Optimised Geometry with frequency analysis (B3LYP/LANL2DZ for Mo and B3LYP/6-311G for other elements) of the cis-[Mo(OH2)2(CO)4]: DOI:10042/to-13197
Miniproject: Towards Rational Design of Disilyne Coordination Compounds
Transition metal alkyne complexes are involved in synthetically useful reactions such as the Pauson-Khand reaction and de novo synthesis of functionalised benzene via alkyne trimerisation. The electron-rich nature of the carbon-carbon triple bond renders alkyne coordination especially facile, and the availability of 2 sets of orthogonal π-type orbital meant that alkynes can act as a two electron (L type) donor ligand or as four electron (L2 type) ligand.
In 2004, Sekiguchi et al. [10] synthesized the first disilyne and reported its crystal structure. The Sekiguchi synthesis utilises an bulky group on silicon to kinetically stabilise the disilyne species from dimerisation, and this hinders further functionalisation of the disilyne group. Moving down Group 14, the valance orbitals becomes more diffuse, and one would expect better match in size between valance orbitals in Si and valance orbitals on the metal center and better coordination. In 2009, Sekiguchi et al. reported a coordination complex of disilyne to potassium as a product of one-electron reduction of disilyne by elemental potassium. The nature of the silicon-potassium bond is conformed by X-ray crystallography and EPR spectroscopy, where hyperfine couplings to 39K and 41K nuclei are seen. [11]
However, to-date transition metal coordinated disilyne remains elusive. Coordination complexes of disilylene, a silicon version of alkene, have been reported in the literature [12] [13] Such complexes demand less bulky substituents on Si as the coordinated disilyne is significantly less reactive than the uncoordinated counterpart. It is thus interesting to explore the electronic structure of hypothetical disilyne coordination complex, and access, at a theoretical level, the practical viability of such complexes.
As such, the mini project aims to uncover the electronic structure of hypothetical disilyne complexes in comparison to corresponding alkyne complex and see whether disilyne coordination is more facile than acetylene coordination.
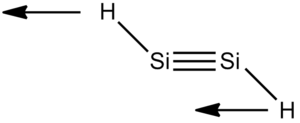
The Structure and Bonding in Disilyne
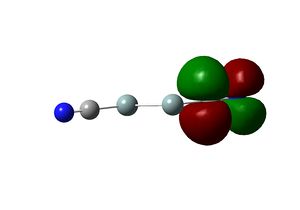
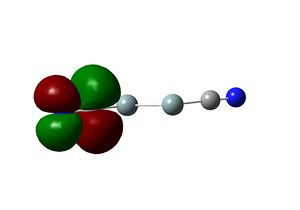
The structure of disilyne is rather different compared to that of alkyne. All isolated disilyne species are unambiguously trans-bent. In order to investigate the origin of this strutural preference, a qualitative LCAO approach is used. In order to simplify the analysis, the simplest Si2H2 and C2H2 are considered. Molecular orbitals of acetylene are constructed by first considering the fragment molecular orbitals of the C2 before combining, in a symmetry adopted manner, with the H-H fragment.
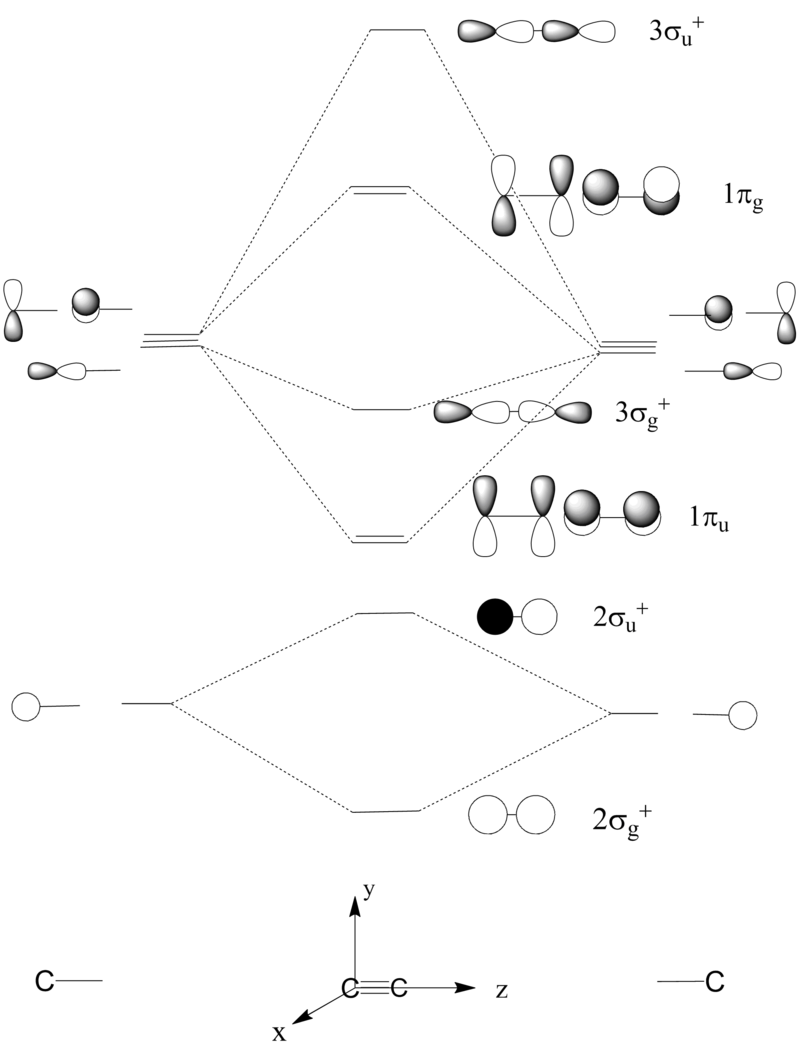
In the qualitative MO diagram, the 1πu level is lower in energy than the 3σg. This is because of strong s-p mixing. The s-p mixed orbitals are not shown for clarity - the mixing will be analysed when the C2 fragment is combined with H2 fragment.
The qualitative MO diagram of acetylene correlates well with the calculated molecular orbitals at B3LYP/6-311+G(d,p) level. The effect of trans-bending investigating using qualitative Walsh correlation diagram between the D∞h linear form and C2h trans-bent form.
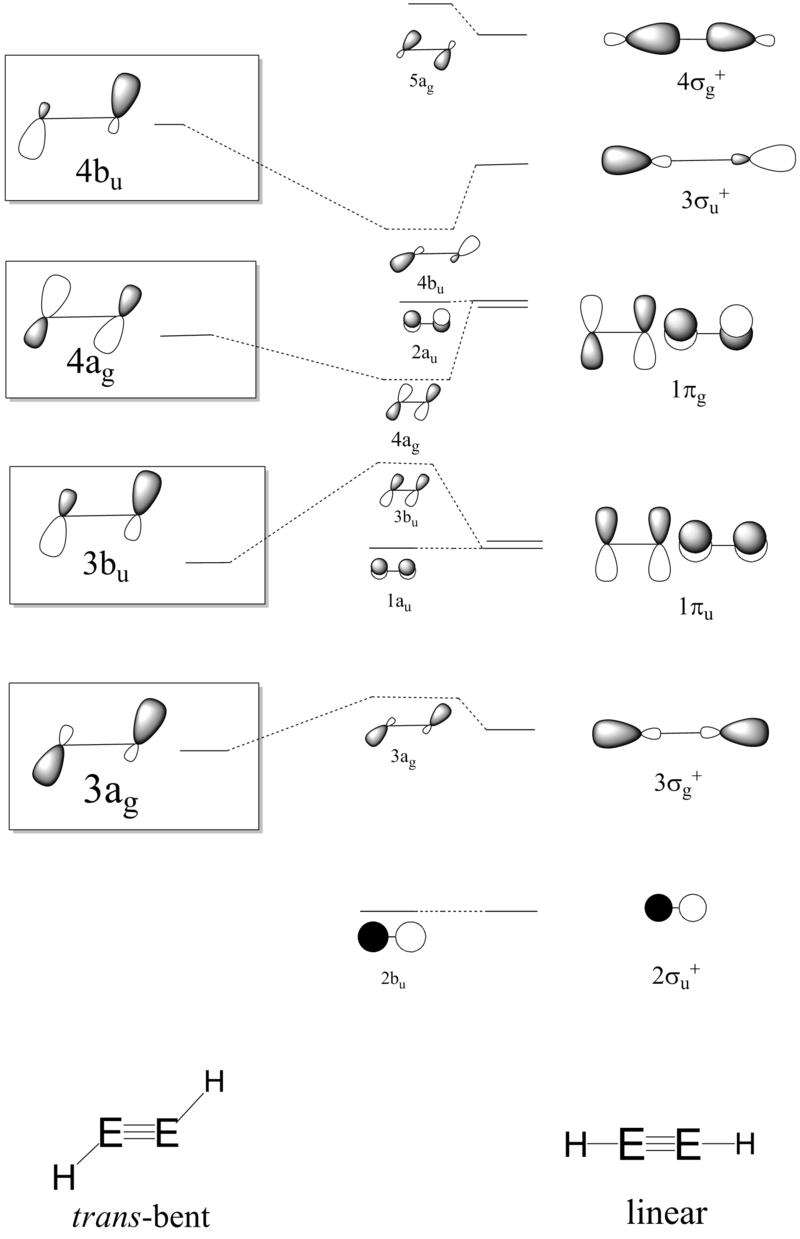
Qualitatively, as the molecule deviates from linearity, the bonding 3σg+ assumes antibonding character and raises in energy. Analogously, the anti-bonding 3σu+ assumes bonding character and lowers in energy. The in-plane π type interactions weakens as the geometry changes from linear to trans-bent as p orbitals overlap less well in the trans-bent geometry, but the out-of-plane π bond is unaffected. This breaks the degeneracy in the the 1πg and 1πu levels, and the poorer spatial overlap meant that the anti-bonding π orbital is less anti-bonding (the energy is lowered) and the bonding π orbital is less bonding (the energy is increased). In the C2h symmetry, 3σg+ (3ag) can mix with empty anti-bonding 1πg (4ag). Correspondingly, the empty 3σu+ (4bu) can mix with bonding 1πu (3bu). The relative energy of 4ag and 2au, 3bu and 1au is subtle and depends on the strength of orbital mixing. This qualitative Walsh diagram shows that the strength of the mixing determines whether the trans bent geometry is favoured over linear. Using the Klopman-Salem equation derived from second-order perturbation theory, the stabilisation energy from orbital interaction Estab depends on overlap integral between the orbitals S2 and energy separation ΔE,
Estab=S2/ΔE.
Therefore, the closer in energy between the orbital being mixed, the stronger is the favorable energy reduction from mixing. As one moves down the group, the valance orbital becomes more diffuse, thus the extent of overlap worsens. This decreases the energy gap between antibonding and bonding level thus enables very favourable mixing. In order to obtain further insight into the LCAO composition of disilyene, the coupled cluster formalism is used to calculate the equilibrium geometry and electronic structure of disilyne. Coupled cluster theory corrects the treatment of electron exchange in Hatree-Fock theory by using an exponential cluster operator T and implements the ansatz
|CC>=exp(T)|HF>
T=T1+T2+T3...
where |CC> is the wavefunction obtained using coupled cluster theory and |HF> is the wavefunction obtained using Hatree-Fock theory. The cluster operator T is written in terms of creation â+ and annhilation â operators of occupied orbitals (i,j) and unoccupied orbitals (α,β). T1 is the single excitation operator, T2 is double excitation and so on.
T1=Sum(Sum(tαiâi âj+,all i),all α)
T2=Sum(Sum(tαi;βjâiâj âα+âβ+,all i,j ),all α,β)
where tαi and tαi;βj are constants to be solved.
The qualitative MO diagram above correlates well with disilyne calculated at the CCSD level using Dunning's correlation consistent, triple zeta basis set cc-pvtz. The correlation consistent basis sets are designed and benchmarked with coupled cluster theory and therefore can be expected to be compatible with the CCSD method. [14]
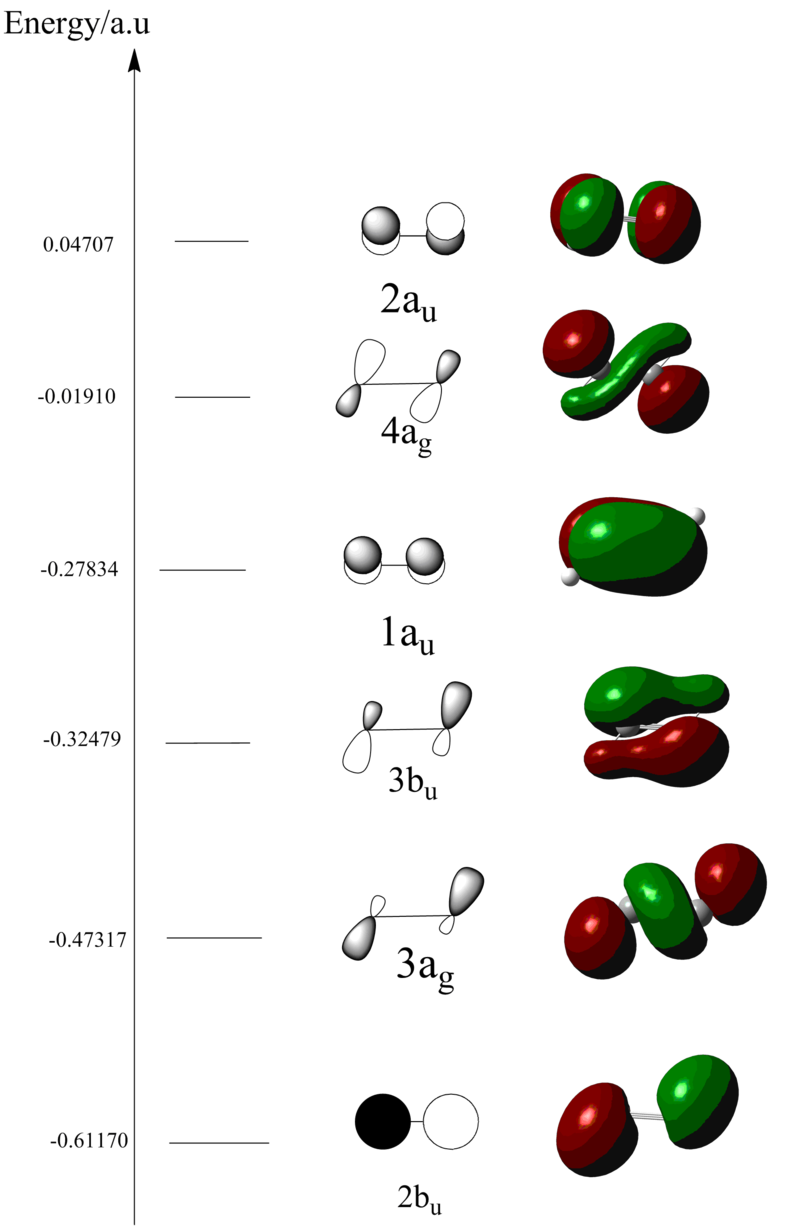
A trans-bent angle of 125.39o and Si-Si bond length of 2.110Â is obtained. This is somewhat shorter than the bond length of all isolated species containing the Si-Si double bond, which lies between 2.138Â and 2.251Â [15]. The vibrational frequency of the structure is all positive, suggesting a stable structure has been obtained.
Endo Product |
| Frequency | Intensity | Symmetry of Vibration | Form of Vibration |
|---|---|---|---|
| 273.6181 | 37.8726 | Bu | Si-H in plane asymmetric bending  |
| 278.0592 | 38.6117 | Au | Si-H out of plane asymmetric bending  |
| 566.7597 | 0.0000 | Ag | Si-Si stretching  |
| 620.7106 | 0.0000 | Ag | Si-H in plane symmetric bending  |
| 2209.4795 | 0.0000 | Ag | Si-H symmetric stretching  |
| 2213.6524 | 125.2297 | Bu | Si-H asymmetric stretching  |
An alternative rationalisation of the trans-bent geometry is the "donor-acceptor" model. In which it is argued that the large doublet-quartet separation energy in the SiH fragment due to widening s-p energy gap down Group 14 and weak Si-Si π bond meant that spin-pairing of electron between two SiH fragment is not possible, thus the system adapts a donor-acceptor type bond.
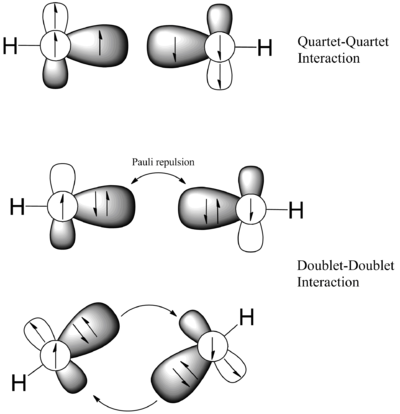
In order to access the validity of the donor-acceptor model, the energies of the doublet and quartet SiH are calculated at the CCSD/cc-pvtz level and are compared with CH.
| CH | SiH | |
|---|---|---|
| Doublet | -38.40709610 | -289.54353088 |
| Quartet | -38.38301064 | -289.48309159 |
| ΔED->Q/au | 2.4085x10-2 | 6.0439x10-2 |
From the table above, it is clear that the doublet-quartet promotional energy is much higher for SiH than CH. Converting to kJ/mol, ΔΔED->Q between SiH and CH is 95 kJ/mol (2 s.f), which is around 30% of the bond energy of a Si-Si single bond (assuming bond strength of Si-Si single bond is 74 kcal/mol, which is a reasonable value taken from calorimetric measurements reported in the literature). [16] Thus the singlet-triplet promotional energy is a reasonable justification of the trans-bent preference.
It is thus interesting to examine the substituent effect on the geometry of disilyne and its vibration frequency. In order to benchmark the less expensive computation methods in comparison with the highly accurate coupled cluster theory, separate calculations on disilyne are ran using less computationally expensive MP2/cc-pvtz and B3LYP/6-311+G(d,p). The former treates electron correlation in a perturbative sense (second order perturbation in the case of MP2) and the later treats electron correlation in a semi-phenomenological sense (in the parametrisation of the exchange functional in B3LYP).
| Si-Si bond length | % deviation from CCSD | H-Si-Si trans bent angle | % deviation from CCSD | |
|---|---|---|---|---|
| CCSD/cc-pvtz | 2.10988 | 0 | 125.390 | 0 |
| MP2/cc-pvtz | 2.10165 | -0.39% | 125.881 | 0.39% |
| B3LYP/6-311+G(d,p) | 2.10599 | -0.18% | 124.771 | -0.49% |
The above table showed that all three methods differ by less than 1 percent. Thus the least computationally demand method B3LYP/6-311+G(d,p) is adopted. Structures of R2Si2 motif is optimised using B3LYP/6-311+G(d,p), where R varies from inductive electron donating (R=SiH3), inductive electron withdrawing (R=F), resonance electron donating (R=Ph) and resonance electron withdrawing (R=CN).
| Si-Si bond length | Si-Si vibration frequency | R-Si-Si trans bent angle | R-Si-Si-R dihedral angle | List of vibrational frequencies | |
|---|---|---|---|---|---|
| R=H | 2.10599 | 566.7597 | 125.390 | 180.000 | 273.6181, 278.0592, 566.7597, 620.7106, 2209.4795, 2213.6524 |
| R=SiH3 | 2.09548 | 651.82 | 130.158 | 180.000 | 19.24, 27.18, 27.70, 34.04, 136.94, 325.06, 412.44, 480.23, 512.39, 520.45, 539.24, 651.82, 863.92, 893.06, 944.57, 944.58, 945.47, 946.40, 2213.62, 2215.64, 2227.72, 2227.96, 2228.16, 2228.52 |
| R=F | 2.24428 | 339.23 | 118.965 | 180.00 | 1 negative frequency seen at -55.78, corresponding to Si-F symmetric out of plane bending. -55.78, 93.44, 191.72, 410.57, 811.07, 836.74 |
| R=Ph | 2.14846 | 550.67 | 125.866 | 155.303 | 19.38, 23.65, 26.11, 53.13, 81.65, 154.03, 179.58, 220.53, 224.22, 333.07, 388.56, 401.4536, 401.62, 447.43, 464.86, 550.67, 629.88, 630.02, 700.13, 703.76, 704.81, 715.77, 747.77, 750.06, 863.72, 863.81, 938.9767, 939.3062, 993.5900, 993.7113, 1011.3033, 1011.6330, 1012.0889, 1012.2755, 1043.1788, 1043.2939, 1091.2163, 1091.3629, 1097.11, 1099.47, 1183.79, 1183.80, 1208.59, 1209.59, 1297.17, 1298.35, 1349.35, 1349.52, 1454.94, 1455.73, 1502.96, 1503.45, 1598.60, 1598.82, 1616.62, 1616.90, 3157.54, 3157.56, 3163.61, 3163.61, 3173.73, 3173.76, 3182.61, 3182.66, 3189.50, 3189.69 |
| R=CN | 2.14578 | 459.20 | 119.389 | 180.000 | 1 negative frequency seen at -35.01, corresponding to Si-F symmetric out of plane bending. -35.01, 41,98, 134.14, 263.63, 287.34, 289.34, 307.44, 459.20, 607.15, 678.66, 2234.67, 2236.63 |
Curiously, optimisation of the dicyano and difluro disilyne at the MP2/cc-pvtz level yields all real frequencies and slightly different structural parameters. This shows that electron correlation may play a crucial role in determining the topology of the potential energy surface in this case.
| Si-Si bond length | Si-Si vibration frequency | R-Si-Si trans bent angle | R-Si-Si-R dihedral angle | ||
|---|---|---|---|---|---|
| R=H | 2.10165 | 623.32 | 125.881 | 180.000 | |
| R=SiH3 | 2.1000 | 681.80 | 130.384 | 180.000 | |
| R=F | 2.21755 | 451.07 | 121.055 | 180.00 | 1 negative frequency seen at -55.78, corresponding to Si-F symmetric out of plane bending. -55.78, 93.44, 191.72, 410.57, 811.07, 836.74 |
| R=CN | 2.13303 | 485.35 | 120.593 | 180.000 |
The (IR-inactive) stretching frequency of Si-Si bond correlates well with the bond length, suggesting a direct relationship between bond length and bond strength. Inductive electron withdrawing substituents such as F decreases the Si-Si bond strength and renders the structure more trans-bent. This can be rationalised using the natural bonding orbital formalism in terms of two strong п(Si-Si)->σ*(Si-F) overlap.
| Donor п(Si-Si) | Acceptor σ*(Si-F) | Interaction Energy/kcal mol-1 |
|---|---|---|
 |
 |
17.74 |
|
 |
17.74 |
The electronegative F lowers σ*(Si-F) and enable good energy match to п(Si-Si). This weakens the Si-Si bond and enhances the preference for trans bent geometry as the σ*(Si-F) and п(Si-Si) overlap is maximal when the substitutents are orthogonal to Si-Si bond.
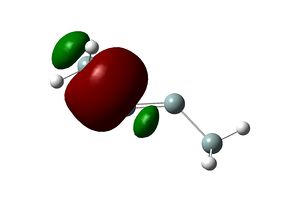
The SiH3 substituent, being electron releasing, has the opposite effect. The dominant stereoelectronic interaction in this case is between σ(Si-Si) and very weakly bonding, empty п(Si-Si). The bonding character of п(Si-Si) arises from some overlap between the small lobes pointing to the center of the molecule (coloured green). Therefore, electron donation strengthens the Si-Si bond. The geometric preference is rationalised by decreasing bonding character (i.e. decreasing overlap of the "green" region) when the molecule becomes more trans bent.
| Donor σ(Si-Si) | Acceptor п(Si-Si) | Interaction Energy/kcal mol-1 |
|---|---|---|
 |
 |
8.60 |
 |
|
8.60 |
In the cyano substituted disilyne, the dominant interaction is that between п(Si-Si)->п*(C-N). This weakens the Si-Si bond, thus increase thetrans-bent preference.
| Donor п(Si-Si) | Acceptor п*(C-N) | Interaction Energy/kcal mol-1 |
|---|---|---|
 |
 |
13.90 |
|
 |
13.90 |
 |
 |
8.23 |
|
 |
8.23 |
The opposite is occurring in the case of phenyl substituted disilyne. Considering the qualitative Walsh diagram above, in the theoretical linear species, enhanced conjugation with the phenyl group lowers the п-п* gap whilst leaving the energies of σ and σ* inteact. This increases the п-σ* and п*-σ gap, thus decrease the extent in which orbital mixing occurs upon distortion to trans-bent, thus diminishes the extent in which trans bent is favoured.
CCSD/cc-pvtz optimised disilyne (with frequency and MO analysis): DOI:10042/to-12964
MP2/cc-pvtz optimised disilyne (with frequency and MO analysis): DOI:10042/to-12965
B3LYP/6-311+G(d,p) optimised disilyne (with frequency and MO analysis): DOI:10042/to-12966
B3LYP/6-311+G(d,p) optimised difluro disilyne (with frequency and MO analysis): DOI:10042/to-13063
B3LYP/6-311+G(d,p) optimised diphenyl disilyne (with frequency and MO analysis): DOI:10042/to-13064
B3LYP/6-311+G(d,p) optimised dicyano disilyne (with frequency and MO analysis): DOI:10042/to-13065
MP2/cc-pvtz optimised dicyano disilyne (with frequency and MO analysis): DOI:10042/to-13067
B3LYP/6-311+G(d,p) optimised bis(trihydrosilyl) disilyne (with frequency and MO analysis): DOI:10042/to-13066
MP2/cc-pvtz optimised bis(trihydrosilyl disilyne (with frequency and MO analysis): DOI:10042/to-13068
Disilyne as two electron donor (L type) ligand
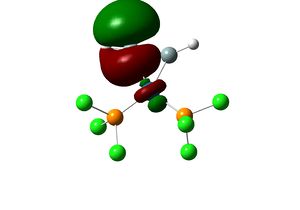
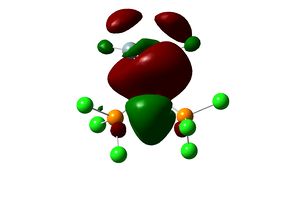
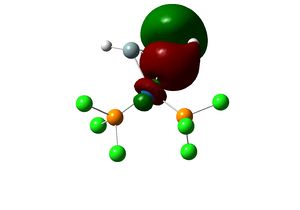
After establishing the electronic structure of the disilyne, the properties of disilyne as a two electron donor ligand is investigated. To this end, model system consist of [L2(disilyne)Pt(0)] motif is constructed. η2 alkyne complexes of Pt(0) such as [(PPh3)2(Ph2C2)Pt(0)] are known in the literature [17]. They are frequently used as model compounds to study the interaction between metal and alkyne in heterogeneous catalysis. The electronic structure of the complex can be considered using a qualitative MO diagram. Using the isolobal analogy, the fragment molecular orbital diagram for PtL2 is first constructed.
Considering the acetylene ligand coordinating coplanar with the for simplicity PtL2 in an η2 manner, the full molecular orbital diagram can be derived from overlap of the PtL2 frontier fragment orbitals with the acetylene frontier orbitals derived above. The resulting qualitative Mo diagram compares well with calculated MO using B3LYP/6-311+G(d,p) for main-group element and pseudopotential LAND2LZ for the platinum centre.
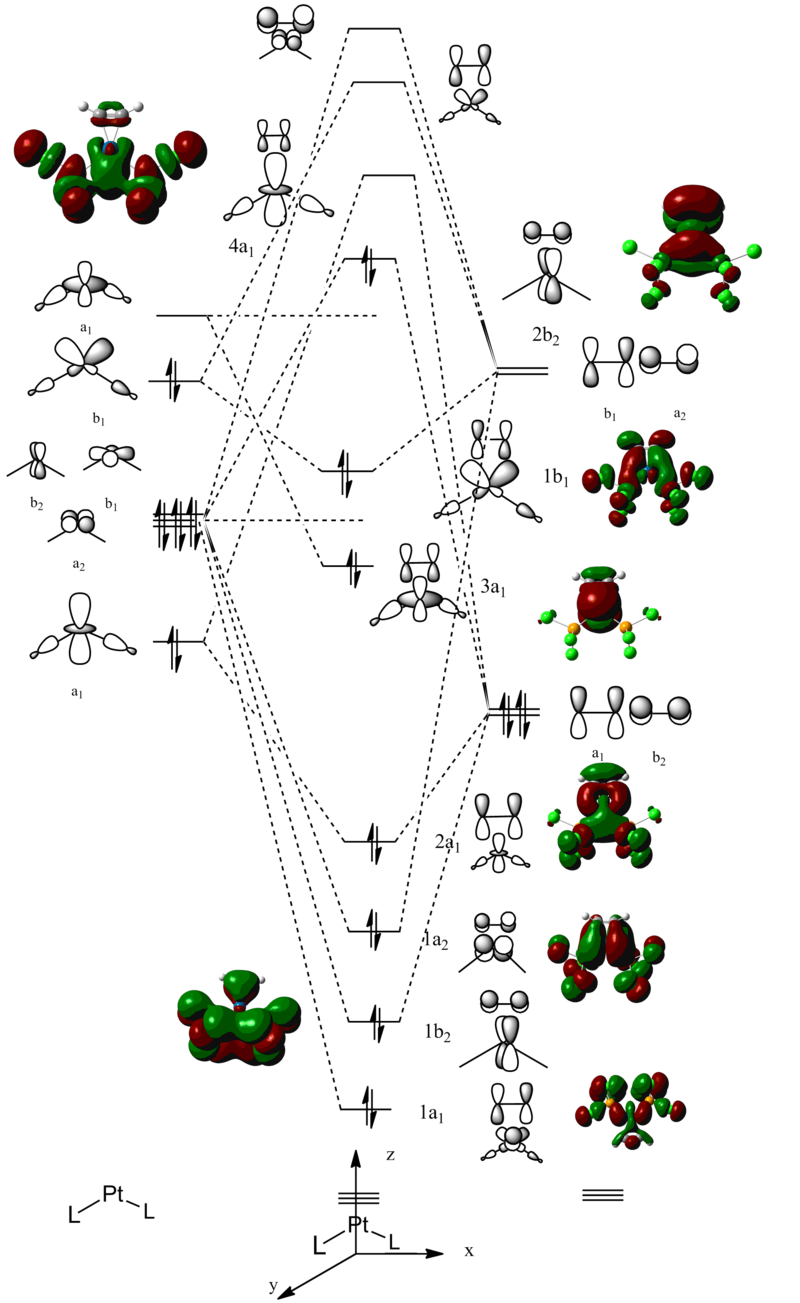
The frontier orbitals can be summerised using the Dewar-Chatt-Duncanson model [18] of alkyne to metal π->d donation followed by metal to alkyne d->π* back donation.
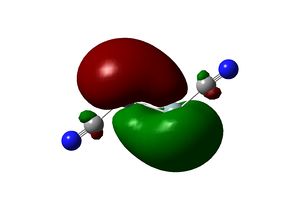
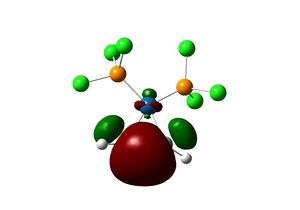
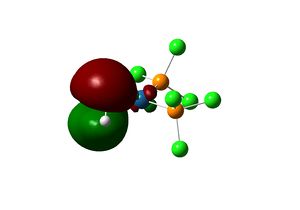
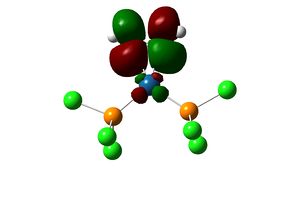
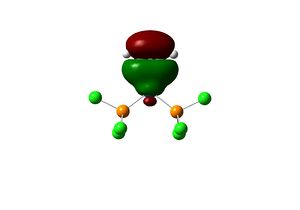
The complex [(PCl3)2(Si2H2)Pt(0)] is first considered. The geometry of the optimised structure of the disilyne complex is markedly different from that of the alkyne complex. The disilyne ligand is twisted with respect to the P-Pt-P plane. One can define a twist angle τ and H-Si-Si-H dihedral angle θ to describe the geometry. All frequencies are positive, suggesting an equilibrium structure has been obtained.
Endo Product |
The twist angle can be measured by introducing a dummy atom (B) in the mid-point of the Si-Si bond, measuring the Si-B-Pt-P dihedral angle from both silicon then taking average. A τ=28.754o and θ=137.534 is obtained. The Si-Si bond length in the complex is 2.179 Â. The twisting of the Si-Si bond with respect to the P-Pt-P plane can be rationalised in terms of the tilted nature of the π bonds. In fact, the molecular orbitals interaction of the disilyne complex is analogous with the alkyne complex.
| Donor | Acceptor | Interaction Energy/kcal mol-1 | Form of interation |
|---|---|---|---|
 |
 |
180.50 | disilyne to metal п->d donation |
 |
|
178.38 | disilyne to metal п->d donation |
 |
|
33.72 | disilyne to metal σ->d donation |
 |
 |
25.98 | disilyne to metal п->d donation |
The NBO analysis reveals that the п->d donation dominates over d->π* back donation in the case of disilyne coordination. This is less so in the case of acetylene coordination.
| Donor | Acceptor | Interaction Energy/kcal mol-1 | Form of interation |
|---|---|---|---|
 |
 |
51.30 | metal to disilyne d->п* donation |
 |
 |
103.71 | disilyne to metal п->d donation |
 |
|
63.16 | disilyne to metal σ->d donation |
Charge distribution analysis using NBO provides further indication of weak backbonding in the case of disilyne coordination. The platinum center in disilyne carries negative partial charge whereas the Si atom is more positive in the coordinated disilyne compared to the free disilyne, showing large degree of electron donation from silyne to metal centre. The opposite effect is operating in alkyne complex, where the carbon on free acetylene is less negative than the coordinated acetylene, suggesting a strong back donation operating.
| NBO Charge | |
|---|---|
| Si (in free disilyne) | 0.136 |
| Si (in coordinated disilyne) | 0.329/0.339 (the charge on the two silicon atoms are slightly different) |
| C (in free alkyne) | -0.156 |
| C (in coordinated alkyne) | -0.278 |
| Pt (in disilyne complex) | -0.876 |
| Pt (in disilyne complex) | -0.341 |
In order to study the effect of ligand on the structure of disilyne complexes in comparison with the alkyne complexes, the electron donating PCl3 ligand is replaced with strong π acid CO. The geometry is optmised using B3LYP/6-311+G(d,p)/LANL2DZ. All frequencies are real, corresponding to an equilibrium structure.
| L=PCl3 | L=CO | |
|---|---|---|
| Si-Si bond length/Â | 2.179 | 2.161 |
| Pt-Si bond length/Â | 2.409 | 2.432 |
| Twist angle τ | 28.754 | 23.629 |
| Dihedral angle θ | 137.534 | 126.193 |
| Si-Si stretch frequency | 552.49 | 568.79 |
The carbonyl ligand decreased the Si-Si bond length and increased the Si-Si stretching frequency. This can be rationalised in terms of less back donation to п* of Si-Si as the carbonyl ligand is competing for electron density, and less п donation into the metal orbital as the carbonyl ligand lowers the energy of the metal d-orbital and thus allow less п->d donation. This results in stronger Si-Si bond at the expense of weaker Pt-Si bond.
On the other hand, varying the substituents on the Si-Si bond can also exert a large effect on disilyne-platium bond. To this end, model system consist of [(PCl3)2(R2Si2)Pt(0)] is modeled with R=SiH3 and F to see the effect of electron donating and withdrawing substituents.
| R=H> | R=SiH3 | R=F | |
|---|---|---|---|
| Si-Si bond length/Â | 2.179 | 2.163 | 2.370 |
| Pt-Si bond length/Â | 2.409 | 2.423 | 2.374 |
| Twist angle τ | 28.754 | 21.866 | 50.431 |
| Dihedral angle θ | 137.534 | 121.858 | 150.991 |
| Si-Si stretch frequency | 552.49 | 629.95 | 349.94 |
From above table, it is clear that Pt-Si bond length is lowest for R=F. As analyzed above for disilyne, electron withdrawing substituent lowers the energy of п* so as to enable better back donation. This strengthens the Pt-Si bond at the expense of the Si-Si bond. The strong trans-bent geometry can be rationalised using the NBO overlaps of disilyne discussed above. The drop in σ*(Si-F) enables greater degree of σ-π mixing in disilyne. This renders the π orbitals more tilted thus forces the disilene to coordinate in a highly twisted manner. The converse if occurring in R=SiH3, where electron donating group causes raises the energy of the π orbital thus allow less efficient π-d energy match.
The bonding situation in disilyne complex compared to the acetylene complex can be further analyzed using the Wiberg bond index. The Wiberg bond index is related to the earlier Coulson bond index and is physically measuring the degree to which the different orbitals have significant simultaneous in phase contributions from the basis orbitals of both atoms in question. The Wiberg bond index is frequently invoked in the literature to study heavier main group multiple bonding. [19]
| R=H | R=F | R=SiH3 | |
|---|---|---|---|
| Pt-C | 0.85 | 0.95 | 0.78 |
| Pt-Si | 1.06 | 1.18 | 0.99 |
| C-C | 2.34 | 1.99 | 2.33 |
| Si-Si | 1.82 | 1.23 | 1.80 |
The Wilberg bond order analysis agreed with observation of the structural parameters. Electron donating substituent on the disilyne enhances the Si-Si bond in the expense of Si-Pt bond. The converse is true for electron withdrawing substituent. The same trend is mirrored in acetylene complexes. Comparing the Wiberg bond index, it seems that Si-Pt bond has larger bond order than C-Pt bond. In order to confirm this, Quantum Theory of Atoms-in-Molecule analysis is performed on the wavefunction to investigate its topology using Multiwfn 2.3.1. One bond critical point each is seen between the each carbon and platinum in the acetylene complex and between each silicon and platinum in the disilyne complex.
| ρ(r)/a.u. | grad(grad(ρ(r))) | |
|---|---|---|
| R=F | 0.128 | 0.255 |
| 0.128 | 0.255 | |
| R=SiH3 | 0.101 | 0.254 |
| 0.101 | 0.253 | |
| R=H | 0.111 | 0.260 |
| 0.111 | 0.260 |
| ρ(r)/a.u. | grad(grad(ρ(r))) | |
|---|---|---|
| R=F | 0.0893 | -0.0776 |
| 0.0896 | -0.0787 | |
| R=SiH3 | 0.0797 | -0.0474 |
| 0.0790 | -0.0435 | |
| R=H | 0.0825 | -0.0539 |
| 0.0826 | -0.0562 |
QTAIM analysis agrees with analysis of Wiberg bond index - both predicts a stronger Pt-Si bond with electronegative substituent. This can be seen by greater electron density in the bond critical point, a greater value of the Laplacian of electron density, indicating greater degree of covalancy. However, QTAIM suggests that the electron density in Pt-Si bond is significantly less than that of Pt-C bond, in contrary to prediction of Wiberg bond index. A possible ratioanlisation is that the Pt-Si bond and longer and more diffuse than Pt-C, therefore electron density at a single point does not totally reflect the bond order. Wiberg bond index, however, takes into account all electrons in overlapping orbitals and hence give a better indication of bond strength.
Conclusion
The bonding of disilyne to metal complexes is similar to the Dewar-Chatt-Duncanson model for alkyne coordination. More electron withdrawing substituents favours backbonding and enhances the metal-silicon bond. However, it is ambiguous whether disilyne complexes are more stable than alkyne complex. Although orbitals in disilyne is higher in energy thus can overlap better with metal orbitals, they are necessarily more diffuse. Wiberg bond index and QTAIM gives divergent results and further analysis (for example electron localisation function) is needed to confirm the stability of the Si-Pt bond.
Logfile
B3LYP/6-311+G(d,p)/LAND2LZ optimised (transition) structure of [Pt(CO)2(Si2H2)]: DOI:10042/to-12953
Vibrational analysis of B3LYP/6-311+G(d,p)/LAND2LZ optimised (transition) structure of [Pt(CO)2(Si2H2)]: DOI:10042/to-12975
B3LYP/6-311+G(d,p)/LAND2LZ optimised (stable) structure of [Pt(CO)2(Si2H2)] with vibrational analysis: DOI:10042/to-12978
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(PCl3)2(Si2H2)]: DOI:10042/to-12967
Vibrational analysis of B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(PCl3)2(Si2H2)]: DOI:10042/to-12977
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(CO)2(C2H2)]: DOI:10042/to-12968
Vibrational analysis of B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(CO)2(C2H2)]: DOI:10042/to-12974
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(PCl3)2(C2H2)]: DOI:10042/to-12969
Vibrational analysis of B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(PCl3)2(C2H2)]: DOI:10042/to-12976
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(PCl3)2(Si2F2)]: DOI:10042/to-12972
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of [Pt(PCl3)2(C2F2)]: DOI:10042/to-12973
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of "disilylidene" [Pt(PCl3)2(Si2H2)]: DOI:10042/to-12979
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure of "vinylidene" [Pt(PCl3)2(Si2H2)]: DOI:10042/to-12980
B3LYP/6-311+G(d,p)/LAND2LZ optimised structure [Pt(PCl3)2(Si2(SiH3)2)]: DOI:10042/to-13149
References
- ↑ A. D. Becke, "A new mixing of Hartree–Fock and local density‐functional theories ", Journal of Chemical Physics, 1993,90, 1372, DOI:10.1063/1.464304
- ↑ A. D. Becke, "Density‐functional thermochemistry. III. The role of exact exchange", Journal of Chemical Physics, 1993,98, 5648, DOI:10.1063/1.464913
- ↑ F. H. Allen, I. J. Bruno, "Bond lengths in organic and metal-organic compounds revisited: X—H bond lengths from neutron diffraction data ", Acta Crystallography B, 2010,66, 380-386, DOI:10.1107/S0108768110012048
- ↑ 4.0 4.1 J. Glaser, "Crystal and Molecular Structure of Thallium(III) Bromide Tetrahydrate and Thallium(III) Chloride Tetrahydrate, a Redetermination", Acta Chemica Scandinavica, 1979,A33, 789, DOI:10.3891/acta.chem.scand.33a-0789
- ↑ R. Bader, "A quantum theory of molecular structure and its applications", Chemical Reviews, 1991,91, 893, DOI:10.1021/cr00005a013
- ↑ F.A. Cotton, D.J. Darensbourg, S. Klein, B. W. S. Kolthammer, "Steric contributions to the solid-state structures of bis(phosphine) derivatives of molybdenum carbonyl. X-ray structural studies of cis-Mo(CO)4[PPh3-nMen]2 (n = 0, 1, 2)", Inorganic Chemistry, 1982,21, 294, DOI:10.1021/ic00131a055
- ↑ D. J. Darensbourg, R. L. Kump, "A convenient synthesis of cis-Mo(CO)4L2 derivatives (L = Group 5a ligand) and a qualitative study of their thermal reactivity toward ligand dissociation", Inorganic Chemistry, 1978,17, 2680, DOI:10.1021/ic50187a062
- ↑ G. Hogarth, T. Norman, "Crystal structures of trans-[Mo(CO)4(PPh3)2] and 1,4-bis (diphenylphosphino)-2,5-difluorobenzene", Inorganica Chimica Acta, 1997,256, 167, DOI:10.1016/S0020-1693(96)05133-X
- ↑ D. J. Darensbourg, M. Y. Darensbourg, "Infrared determination of stereochemistry in metal complexes: An application of group theory, Journal of Chemical Education, 1970,47, 33, DOI:10.1021/ed047p33
- ↑ A. Sekiguchi, R. Kinjo, M. Ichinohe, "A Stable Compound Containing a Silicon-Silicon Triple Bond", Science, 2004,305, 1755, DOI:10.1126/science.1102209
- ↑ A. Sekiguchi, R. Kinjo, M. Ichinohe, "Interaction of π-bonds of the silicon–silicon triple bond with alkali metals: An isolable anion radical upon reduction of a disilyne", Synthetic Metals, 2009,159, 773, DOI:10.1016/j.synthmet.2009.01.007
- ↑ M. Weidenbruch, "Silylenes and disilenes: examples of low coordinated silicon compounds", Coordination Chemistry Reviews, 1994,130, 275, DOI:10.1016/0010-8545(94)80007-3
- ↑ V.Ya. Lee, A. Sekiguchi, in "Organometallic Compounds of Low-Coordinate Si, Ge, Sn and Pb: From Phantom Species to Stable Compounds", John Wiley and Sons
- ↑ K. A. Peterson, T. H. Dunning, "Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited ", Journal of Chemical Physics, 2002,117, 10548, DOI:10.1063/1.1520138
- ↑ P. P. Power, "π -Bonding and the Lone Pair Effect in Multiple Bonds between Heavier Main Group Elements", Chemical Reviews, 1999,99, 3463, DOI:10.1021/cr9408989
- ↑ R. Walsh, "Bond dissociation energy values in silicon-containing compounds and some of their implications", Account of Chemical Research, 1981,14, 246, DOI:10.1021/ar00068a004
- ↑ U. Belluco, R. Bertani, R. A. Michelin, M. Mozzon, "Platinum–alkynyl and –alkyne complexes: old systems with new chemical and physical perspectives", Journal of Organometallic Chemistry, 2000,600, 37, DOI:10.1016/S0022-328X(00)00089-9
- ↑ J. Chatt and L. A. Duncanson, "Olefin co-ordination compounds. Part III. Infra-red spectra and structure: attempted preparation of acetylene complexes", Journal of the Chemical Society, '1953, 2939, DOI:10.1039/JR9530002939
- ↑ Y. Wang, G. H. Robinson, "Unique homonuclear multiple bonding in main group compounds", Chemical Communications", 2009, 5201, DOI:10.1039/B908048A