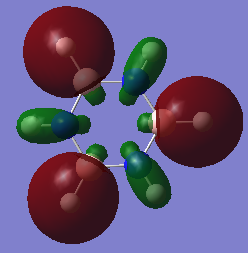Rep:Mod:aa12116
EX3 Section
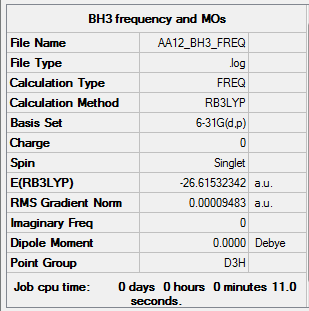
BH3
B3LYP/6-31G (d,p) level
Item Value Threshold Converged? Maximum Force 0.000190 0.000450 YES RMS Force 0.000095 0.000300 YES Maximum Displacement 0.000747 0.001800 YES RMS Displacement 0.000374 0.001200 YES
Low frequencies --- -0.2260 -0.1035 -0.0054 48.0278 49.0875 49.0880 Low frequencies --- 1163.7224 1213.6715 1213.6741
BH3 |
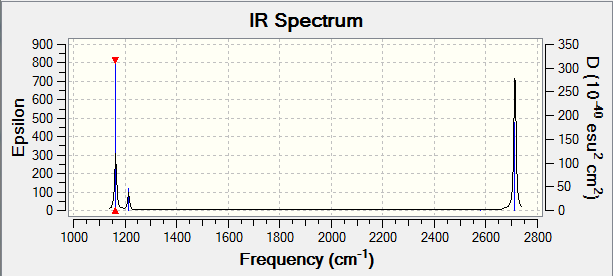
BH3 Vibrations
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1164 | 92 | A2" | yes | out-of-plane bend |
| 1214 | 14 | E' | very slight | bend |
| 1214 | 14 | E' | very slight | bend |
| 2580 | 0 | A1' | no | symmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
The number of expected vibration modes is expected to be 6 as according to the 3N-6 rule. Only 3 peaks are observed in the IR spectrum due to the overlap of of the 2 vibrations at 1214 cm-1 and 2713 cm-1. In addition the peak expected at 2580 cm-1 is IR inactive, therefore not observed in the spectrum.
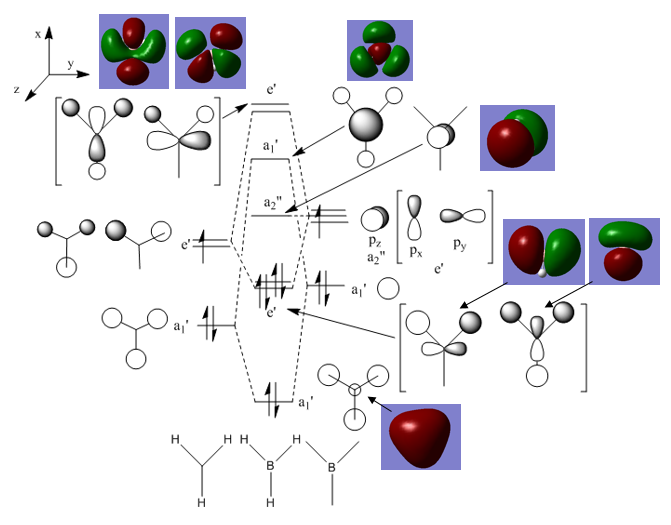
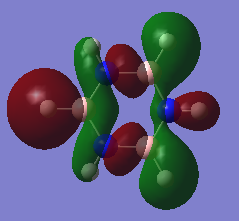
Molecular Orbital Diagram
The qualitative MO theory illustrates the real molecular orbitals with good accuracy. Qualitative MO theory allows visualisation of each real orbital with greater ease, both in terms of mixing and relative size of the orbitals. However, one of the major limitations faced is the lack of representation of the 3D geometry of the molecules and the shape formed by mixing of the orbitals.
Ng611 (talk) 17:44, 30 May 2018 (BST) Good analysis! I would say that lack of 3d representation and the true shape of the orbitals are differences, but they are not the most important of the differences here.
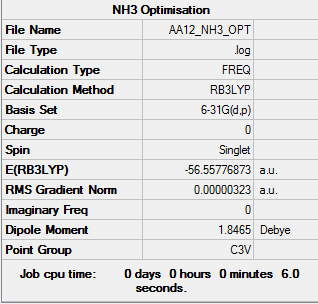
NH3
B3LYP/6-31G (d,p) level
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
Ng611 (talk) 17:45, 30 May 2018 (BST) It appears that you've chopped the bottom off your BH3 log file here.
Low frequencies --- -0.0128 -0.0017 0.0006 7.1032 8.1046 8.1049 Low frequencies --- 1089.3834 1693.9368 1693.9368
NH3 |
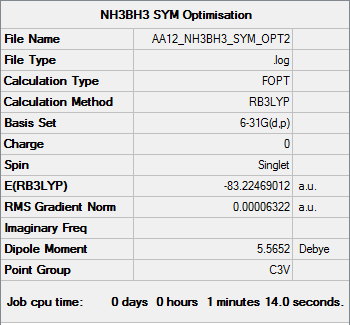
NH3BH3
B3LYP/6-31G (d,p) level
Item Value Threshold Converged? Maximum Force 0.000123 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000585 0.001800 YES RMS Displacement 0.000320 0.001200 YES
Low frequencies --- -0.0573 -0.0499 -0.0075 21.6972 21.7073 40.5564 Low frequencies --- 266.0216 632.3607 640.1371
E(NH3) = -56.55777 a.u.
E(BH3) = -26.61532 a.u.
E(NH3BH3) = -83.22469 a.u.
The association energy of NH3BH3 is given by: ΔE = E(NH3BH3)-[E(NH3) + E(BH3)]
ΔE = -0.0516 a.u. = -129 kJ/mol
Comparison of the N-B bond in NH3BH3 to the isoelectronic C-C bond in ethane shows that the N-B bond is a relatively weak covalent bond.
Ng611 (talk) 17:49, 30 May 2018 (BST) You got the correct value in a.u., but you've converted to Kj/mol incorrectly (you're off by only a few Kj/mol). Remember also to include numerical values of your comparative bond enthalpies and to cite their source.
NH3BH3 |
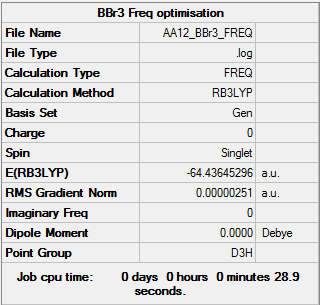
BBr3
B3LYP/6-31G (d,p) level
Ng611 (talk) 18:04, 30 May 2018 (BST) What about LANL2DZ?
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000023 0.001800 YES RMS Displacement 0.000012 0.001200 YES
Low frequencies --- -0.0152 -0.0064 -0.0046 2.1795 2.1796 4.7211 Low frequencies --- 155.9666 155.9686 267.7253
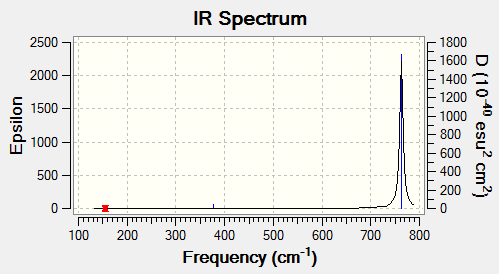
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
| 156 | 0 | E' | no | bend |
| 156 | 0 | E' | no | bend |
| 268 | 0 | A1' | no | symmetric stretch |
| 378 | 4 | A2" | no | out-of-plane bend |
| 763 | 320 | E' | yes | asymmetric stretch |
| 763 | 320 | E' | yes | asymmetric stretch |
BBr3 |
Project Section
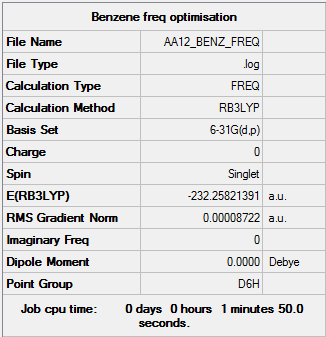
Benzene
B3LYP/6-31G (d,p) level
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000087 0.000300 YES Maximum Displacement 0.000757 0.001800 YES RMS Displacement 0.000321 0.001200 YES
Low frequencies --- -2.1456 -2.1456 -0.0089 -0.0044 -0.0043 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Benzene |
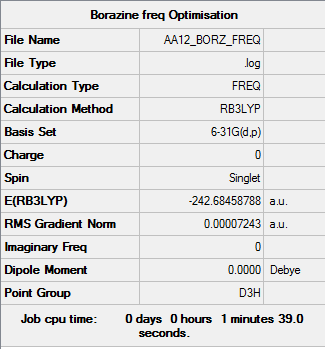
Borazine
B3LYP/6-31G (d,p) level
Item Value Threshold Converged? Maximum Force 0.000219 0.000450 YES RMS Force 0.000072 0.000300 YES Maximum Displacement 0.000496 0.001800 YES RMS Displacement 0.000199 0.001200 YES
Low frequencies --- -11.3207 -11.0997 -10.8975 -0.0105 -0.0094 0.0922 Low frequencies --- 289.0979 289.1066 403.9524
Borazine |
Comparing Benzene and Borazine
| Benzene | Borazine |
|---|---|
 |
 |
| C = -0.239, H = 0.239 | N = -1.102, B = 0.747, B-H = -0.77, N-H = 0.432 |
- Benzene displays equal charge across all carbon and hydrogen atoms. All carbon and hydrogen atoms show a charge of -0.239 and +0.239 respectively. This is a display of the difference in electronegativity between carbon and hydrogen. Carbon is more electronegative, hence the negative value, however, only very slightly as shown by the small charge values given.
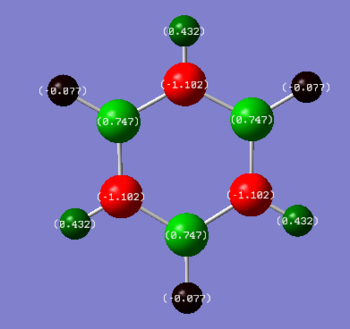
- Borazine's charge distribution shows greater variation than that of Benzene. Hydrogen atoms bonded to a nitrogen show a more positive value due to the greater electonegativity of nitrogen than boron. All N-H hydrogen atoms show a value of +0.432 while B-H hydrogen atoms show a negative value of -0.077. Since hydrogen and boron have a very similar degree of electronegativity, the small negative value of the B-H hydrogen atoms can be attributed to the 0.1 difference in electronegativity between hydrogen and boron (boron and hydrogen have electronegativities of 2.0 and 2.1 respectively). The nitrogen atoms display the most negative value of -1.102 due to having the greatest inherent electronegativity out of the elements in the molecule. This explains the positive value of 0.432 observed in the N-H hydrogen atoms, as the electrons shift towards the nitrogen leaving the hydrogen less shielded. The boron atom shows a more positive charge than the N-H hydrogen, this can be attributed to the bonding of boron to 2 nitrogen atoms, doubling the effect of electron withdrawal on its electrons. In addition bond between boron and hydrogen may also contribute a small amount to the positive boron charge.
- Comparison of the 2 molecules shows that benzene has a more symmetrical charge distribution between the atoms, with each atom of an element having the same charge. Borazine shows lesser symmetry in its charge distribution with varying charges in the hydrogen atoms depending on whether they are bonded to a nitrogen or boron atom. Both molecules are displayed with the same colour range. The dimmer colours displayed on the benzene atoms implies that the relative charge distribution is greater in benzene than borazine. Benzene has a more delocalised system allowing more charge distribution. As for borazine, the molecule is more polarised and the charge distribution is more concentrated on each atom, thus the brighter colours given by the colour scale.
Ng611 (talk) 17:52, 30 May 2018 (BST) Good! What can you say about the relationship between the charge distribution and the rotational symmetry of the molecule (you're right to say that benzene has a more symmetrical distribution, but be more specific). Also what are the sum of the partial charges?
| Benzene MO | Borazine MO | Comparison |
|---|---|---|
|
|
MO17 - Benzene and Borazine display very similar shapes with complete in-phase pi-bonding above and below the plane of the ring. Benzene displays a perfectly symmetric shape along the C-H bond plane with little delocalisation at the hydrogens. Borazine displays a less symmetrical, more skewed, molecular orbital structure with more delocatisation towards the N-H hydrogen atoms and little towards the B-H hydrogen atoms. |
|
|
Benzene MO19, Borazine MO18 - The molecular orbitals are bonding sigma orbitals formed by the overlap of pi-orbitals. Benezene shows a molecular orbital with more symmetry than the molecular orbital of borazine. In benzene, the there is direct overlap of the pi-orbitals with the hydrogen orbitals either side of the ring. The other 4 hydrogen orbitals experience weaker overlap with the p-orbitals of the carbons, shown in red. In borazine, there greater electron density at the B-H hydrogen atoms compared to the C-H hydrogen atoms on benzene. This is due to hydrogens having greater electronegativity than boron, causing a shift in the electron desity towards the hydrogen atoms. However, in contrast to the B-H hydrogen atoms, N-H hydrogen atoms display less electron density in comparison to the hydrogens of benzene. |
|
|
Benzene MO13, Borazine MO16 - These molecular orbitals are constructed purely form hydrogen orbitals. Both orbitals show no direct orbital interaction and only weak through space orbital interactions. These molecular orbitals can be considered as non-bonding orbitals due to the lack of interactions in the MO. In benzene, the all the hydrogen 1s orbitals have equivalent sizes and shapes and are slightly shifted towards the carbon atoms due to the electronegativity of carbon, causing a shift in electron density. Borazine displays a similar structure, however, the size of the N-H hydrogen orbitals is much smaller in size compared to the benzene C-H hydrogen orbitals. This can be attributed to the electronegativity of nitrogen causing a greater shift in the electron density towards the nitrogen. In contrast the B-H hydrogens have a much larger and less distored orbital shape as hydrogen is more electronegative and is able of retaining its electron density. The contents within the ring of the borazine molecule can be considered as artifacts as a result of the computational calculations. |
Ng611 (talk) 17:55, 30 May 2018 (BST) Well done for comparing the correct MOs by shape and not energtic ordering (which is not necessarily reliable). I would include a brief discussion of the why the differences between MOs in these isostructural and isoelectronic molecules exist to improve this section further. Perhaps also consider discussing the constituent AOs that form the MOs and the overall symmetry of the MO.
Aromaticity
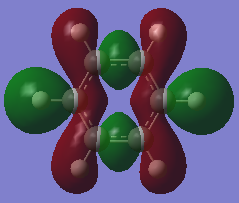
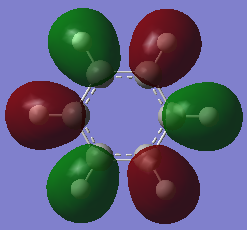
Aromatic compounds can be defined using Huckel's rule, which states that compounds must have a contiguous, cyclic array of p-orbitals perpendicular to the plane of the ring and consist of 4n + 2 π electrons. The presence of 4n + 2 π electrons allows aromatic compounds to display a special type of stability not observed in anti-aromatic compounds. This is often referred to as resonance energy or more commonly aromatic stabilisation.[1]. Example of an observation arising from this stabilisation includes bond lengths between that of a double bond and single bond. The real MOs depict the stability observed in aromatic compounds through the delocalisation of electron density within the ring and around the atoms.
The Pz atomic orbitals are typically used to represent the orbitals perpendicular to the ring. Overlap of these orbitals allows visualisation of electron delocalisation above and below the ring. Although the p-orbital overlap can explain delocalisation, it has limitations as compounds such as a H6 cyclic ring shares some aromatic characteristics of benzene.[2] This suggests that sigma orbitals also contribute to aromaticity, known as σ-aromaticity. This contribution is also viewed in compounds such as benzene, as the lowest energy in-phase bonding molecular orbital shows; 2s orbitals of the carbons form a delocalised orbital structure around and within the entire ring. In addition, p-orbitals in the plane of the ring also mix to display slight delocalisation within the molecule. Visualising the molecular orbitals allows a clear observation of the diffused electron density formed by the p-orbitals overlapping in the plane of the ring to form sigma bonds in aromatic compounds.
It can therefore be concluded that Huckel's theory describes a valid proposal for the identification of the majority of aromatic compounds, however, it fails to account for other contributors to aromoaticity, that can be identified through further molecular orbital analysis, such as σ-aromaticity
Ng611 (talk) 18:03, 30 May 2018 (BST) σ-aromaticity is certainly one of the modern aspects of aromaticity that must be considered -- well done for mentioning it. There several other features that could and should be discussed (e.g.: mobius aromaticity) with relation to aromaticity in molecules besides benzene. You should also consider experimental techniques/results and how they help to shed light on the nature of aromaticity. You have the beginnings of a good discussion, but more detail is needed.
Ng611 (talk) 18:03, 30 May 2018 (BST) This is a good report overall. More detail in your discussion on aromaticity as well as in your MO analysis would improve it further. However, your calculations were correctly performed and the wiki was well laid out. Well done.
References
[1] Palusiak, Marcin & Krygowski, Tadeusz M., Application of AIM parameters at ring critical points for estimation of π-electron delocalisation in six-membered aromatic and quasi-aromatic rings, Chem. Eur. J. 2007, 13, 7996-8006.
[2] Li, Zhen-Hua; Moran, Damian; Fan, Kang-Nian & Schleyer, Paul von Rague, σ-Aromaticity and σ-Antiaromaticity in Saturated Inorganic Rings, J. Phys. Chem. A, 2005, 109, 3711-3716.