Rep:Mod: NW716
NH3 Molecule
Information of NH3
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) in atomic units (au) | -56.55776873 |
| RMS Gradient in atomic units (au) | 0.00000485 |
| Point Group | C3V |
| N-H Bond Length | 1.01798 Å |
| H-N-H angle | 105.74115° |
The literature value of N-H bond length is 1.012 Å and that of H-N-H angle is 106.7°.[1] Hence, calculation using quantum mechanical methods is very accurate. Since the calculation is based purely on quantum mechanics with certain approximations, such as Born–Oppenheimer approximation, there would be small differences between the calculated values and literature values.
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Dynamic Image
NH3 Molecule |
The optimisation file is here.
Vibrational Frequencies

| Mode Number | Wavenumber | Vibrational Mode | Relative Intensity |
| 1 | 1089.54 | N-H wagging (umbrella mode) | 145.3814 |
| 2 | 1693.95 | H-N-H scissoring | 13.5533 |
| 3 | 1693.95 | H-N-H scissoring | 13.5533 |
| 4 | 3461.29 | N-H symmetric stretching | 1.0608 |
| 5 | 3589.82 | N-H asymmetric stretching | 0.2711 |
| 6 | 3589.82 | N-H asymmetric stretching | 0.2711 |
Questions
How many modes do you expect from the 3N-6 rule?
There are four atoms in an ammonia molecule. 3×4-6=6, three vibrational modes are expected.
Which modes are degenerate?
Vibrational modes 2 and 3 are degenerate. Vibrational modes 5 and 6 are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Vibrational modes 1,2 and 3 are "bending" vibrations. Vibrational modes 4, 5 and 6 are "bond stretch" vibrations.
Which mode is highly symmetric?
Vibrational modes 1 and 4 are highly symmetric.
Which one is the "umbrella" mode?
Vibrational mode 1 is the "umbrella" mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Four bands are expected to see in an IR spectrum, a sharp peak at around 1090 cm-1, a lower peak at around 1694 cm-1 and two small peaks at around 3500 and 3590 cm-1
Charge on the N-atom and H-atoms
Charge on N atom: -1.125 e-
Charge on H atom: 0.375 e-

What charge (positive or negative) would expect for N and H and why?
Since N atom is more electronegative than H atom, N atom would have a positive charge and H atom would have a positive charge.
N2 Molecule
Information of N2
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) in atomic units (au) | -109.52412868 |
| RMS Gradient in atomic units (au) | 0.00000060 |
| Point Group | D∞h |
| Bond Length | 1.10550 Å |
The literature value of bond length of nitrogen-nitrogen triple bond is 1.0976 Å.[2] Hence, calculation using quantum mechanical methods is extremely accurate. The small difference, similarly, arises from the approximations used in the calculation.
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Dynamic Image
N2 Molecule |
The optimisation file is here.
Vibrational Frequencies

There is only 3×2-5 = 1 mode of vibration is observed for N2 which is symmetrical stretching. It is IR inactive since there is no change in dipole moment. Hence, the intensity in IR spectrum in the above diagram is zero.
H2 Molecule
Information of H2
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) in atomic units (au) | -1.17853936 |
| RMS Gradient in atomic units (au) | 0.00000017 |
| Point Group | D∞h |
| H-H Bond Length | 0.74279 Å |
The literature value of N-H bond length is 0.74 Å.[3] Hence, calculation using quantum mechanical methods is extremely accurate. Since the calculation is based purely on quantum mechanics with certain approximations, a hydrogen molecule with only two electrons and two protons would give a quite accurate result.
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Dynamic Image
H2 Molecule |
The optimisation file is here.
Vibrational Frequencies
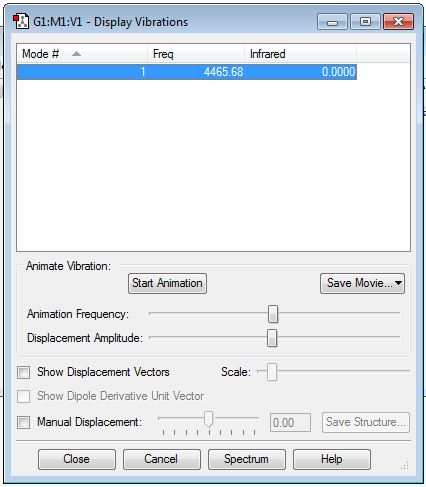
There is only 3×2-5 = 1 mode of vibration is observed for H2 which is symmetrical stretching. It is IR inactive since there is no change in dipole moment. Hence, the intensity in IR spectrum in the above diagram is zero.
Reaction Energies of Formation of Ammonia
E(NH3) = -56.55776873 au
2×E(NH3) = -113.1155375 au
E(N2) = -109.52412868 au
E(H2) = -1.17853936 au
3×E(H2) = -3.53561808 au
ΔE = 2 × E(NH3) - [E(N2) + 3 × E(H2)] = -0.05579074 au = -0.05579074 × 2625.5 kJ/mol = -146.48 kJ/mol (to 2 d.p.)
Since the reaction is exothermic, ammonia gas is more stable than gaseous reactants.
The literature value of the standard enthalpy change of formation of NH3, ΔH°298K = -45.7 kJ/mol.[4] Hence, ΔE = -91.4 kJ/mol. The calculated value above does not comply with the literature value and the difference is large. This is because the calculation methods are different. Hence, the calculated energy of reaction from GaussView is not that accurate.
SiH4 Molecule
Information of SiH4
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) in atomic units (au) | -291.88802760 |
| RMS Gradient in atomic units (au) | 0.00000002 |
| Point Group | TD |
| Si-H Bond Length | 1.48485 Å |
| H-Si-H angle | 109.47112° |
The literature value of N-H bond length is 1.46 Å.[5] Hence, calculation using quantum mechanical methods is relatively accurate for bond length here. Since calculation is based purely on quantum mechanics with certain approximations, the accuracy of the result is slightly affected in this case since there are a lot of electrons in a SiH4 molecule.
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Dynamic Image
SiH4 Molecule |
The optimisation file is here.
Charges on SiH4
Charge on Si atom: 0.629 e-
Charge on H atom: -0.157 e-

Vibrational Frequencies
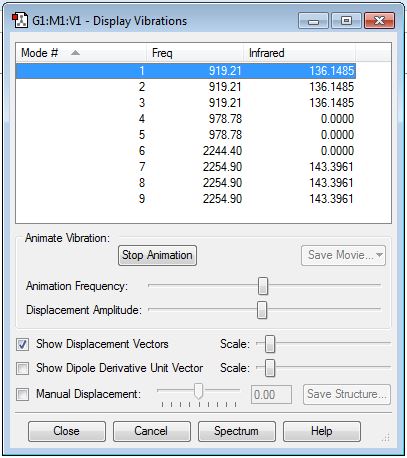
| Mode Number | Wavenumber / cm-1 | Vibrational Mode[6] | Relative Intensity |
| 1 | 919.21 | H-Si-H asymmetrical scissoring | 136.1485 |
| 2 | 919.21 | H-Si-H asymmetrical scissoring | 136.1485 |
| 3 | 919.21 | H-Si-H asymmetrical scissoring | 136.1485 |
| 4 | 978.78 | H-Si-H symmetrical scissoring | 0.0000 |
| 5 | 978.78 | H-Si-H symmetrical scissoring | 0.0000 |
| 6 | 2244.40 | Si-H symmetrical stretching | 0.0000 |
| 7 | 2254.90 | Si-H asymmetrical stretching | 143.3961 |
| 8 | 2254.90 | Si-H asymmetrical stretching | 143.3961 |
| 9 | 2254.90 | Si-H asymmetrical stretching | 143.3961 |
Therefore, two peaks at 919.21 cm-1 and 2254.90 cm-1 are observed in the IR spectrum of SiH4 since only the asymmetrical scissoring and asymmetrical stretching result in a change of dipole moment. The literature values of IR peaks of gaseous SiH4 are 914 cm-1 and 2191 cm-1.[7] Therefore, calculated values using the quantum mechanical method are relatively accurate.
Molecular Orbitals of SiH4
This is a molecular orbital formed by the 2s orbital of the silicon atom. It is very low in energy (-5.28056 au) owing to the high effective nuclear charge of Si. It is occupied by two electrons and does not contribute to bonding (i.e. a non-bonding orbital) as 2s orbital is not a valence orbital.
This is a molecular orbital formed by one of the 2p orbitals of the silicon atom. It is low in energy (-3.63858 au) but higher in energy than the 2s orbital since it is less penetrating. There are three degenerate molecular orbitals contributed by three degenerate 2p orbitals of the silicon atom. It is occupied by two electrons and does not contribute to bonding (i.e. a non-bonding orbital) as 2p orbitals are not valence orbitals.
This is a molecular orbital formed by four 1s orbitals of hydrogen atoms and the 3s orbital of silicon atom, labelled a1. These atomic orbitals are all in phase with each other. It is a bonding orbital occupied by two electrons. It is slightly higher in energy (-0.54726 au) than the non-bonding orbitals. The spherical shape of s orbitals give rise to the tetrahedral shape of the molecular orbital.

This is a molecular orbital formed by symmetry-adapted linear combinations (SALC) of 1s orbitals of hydrogen atoms and one of the 3p orbitals of silicon atom. This molecular orbital is labelled t2. There are three degenerate molecular orbitals contributed since there are three degenerate 3p orbitals of the silicon atom. It is a bonding orbital occupied by two electrons. It is higher in energy (-0.35184 au) than the previous bonding orbital since s orbital and p orbital are not similar in shape and the overlap is less effective. The two distinct phases of 3p orbitals which overlap with the 1s orbitals of hydrogen atoms result in the two symmetrical lobes of the molecular orbital. This is the highest occupied molecular orbital (i.e. HOMO).

This is an anti-bonding molecular orbital formed by symmetry-adapted linear combinations (SALC) of 1s orbitals of hydrogen atoms and one of the 3p orbitals of silicon atom. This molecular orbital is labelled t2*. There are three degenerate molecular orbitals contributed since there are three degenerate 3p orbitals of the silicon atom. It is not occupied. Hence, the bond order of SiH4 is calculated to be (8 - 0) ÷ 2 = 4. It is high in energy (0.05053 au) than the previous orbitals. Similarly, the two phases of 3p orbitals result in the two symmetrical lobes of the molecular orbital. This is the lowest unoccupied molecular orbital (i.e. LUMO).
Reaction Energies of Formation of Silane
E(SiH4) = -291.8802760 au
E(H2) = -1.17853936 au
2×E(H2) = -2.35707872 au
ΔE = E(SiH4)- 2×E(H2) = -289.52319728 au = -289.52319728 × 2625.5 kJ/mol = -760.14 kJ/mol (to 2 d.p.)
The standard enthalpy change of formation of gaseous silane is 34.31 kJ/mol.[8] The above result is reasonable as it requires a large amount of energy to change SiH4 from solid state to gaseous state, an extremely endothermic process.
Reference
- ↑ D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 84th edn., 2003
- ↑ A. E. N. N. Greenwood, Chemistry of the Elements, Butterworth-Heinemann, 2nd edn., 1997.
- ↑ J. McMurry, Fundamentals of Organic Chemistry, Brooks/Cole, 7th edn., 2009.
- ↑ J. M. Modak, Resonance, 2002, 7, 69–77.
- ↑ R. A. BALLINGER and N. H. MARCH, Nature, 1954, 174, 179–179.
- ↑ K. Gaál-Nagy, G. Canevari and G. Onida, J. Phys. Condens. Matter, 2008, 20, 224013.
- ↑ R. Fournier and R. Savoie, Can. J. Chem., 1972, 50, 35–42.
- ↑ J. Malcolm W. Chase, NIST-JANAF Thermochemical Tables, Monograph No.9, American Chemical Society, American Institute of Physics, National Institue of Standards and Technology, 4th edn., 1998.
