Rep:Mod: MgO AW2415
Abstract
When an object absorbs heat it will typically expand. Using computer modelling within both the quasi-harmonic approximation and molecular dynamics, the expansion of a crystal of magnesium oxide has been studied. It was found that the quasi-harmonic approximation was more accurate at lower temperature, however, its predictions broke down as temperature approached the melting point. On the other hand, molecular dynamics predictions were more accurate at higher temperatures. The coefficients of volumetric expansion were found to be 31.7 x10-6 K-1 and 35.2 x10-6 K-1 in the region 600 K – 1300 K for the quasi-harmonic and molecular dynamics methods respectively.
Introduction
The structure of MgO
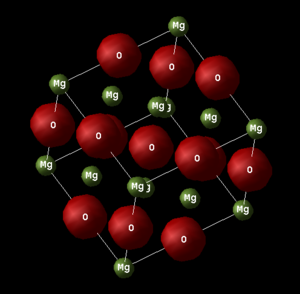
The conventional unit cell of magnesium oxide (MgO), as shown in figure 1, has a face centred cubic (fcc) structure similar to that of rock salt (NaCl). The conventional unit cell contains 4 MgO units and therefore 8 atoms. Since the conventional unit cell is cubic only one lattice parameter, a, is needed (a = b = c).[1]
An alternative representation of the crystal structure is that of a primitive unit cell, which contains just one MgO unit. This is considered a less helpful representation as it doesn’t illustrate the symmetry of the crystal structure as effectively. The connection between primitive and conventional cells is important as it is the volume of a primitive unit cell which is outputted when working within the quasi-harmonic approximation. The volume of the primitive cell can be converted to that of a conventional cell using the following equation:
Equation 1
Where Vc is the conventional cell volume and Vp the primitive cell volume.
A final representation which must be considered is that of a supercell containing 32 MgO units as this is the structure used for molecular dynamics calculations. The volume of a supercell can be converted to that of a conventional cell by dividing by 8.
Thermal expansion
When the temperature increases the volume of an MgO crystal and hence the volume of a conventional unit cell will increase. This expansion can be characterised by a coefficient of volumetric expansion, α, defined as:
Equation 2
For temperature ranges in which the volume increase is linear, α is simply the slope of the plot of V against T.[2]
The quasi-harmonic approximation
The potential energy of a crystalline lattice can, for small displacements be approximated to a parabola. Whilst this model accurately predicts the increase in potential energy with displacement from equilibrium it does not account for the increase in atom-atom separation which is observed when the crystal is heated. In order to account for this we must use the quasi-harmonic approximation. This approximation accounts for the entropic advantage of lower phonon frequencies and hence larger volumes. Only the thermal expansion is considered to behave anharmonically, the lattice dynamics still behave harmonically.[3] Thus, by minimising the free energy for a given phonon frequency it is possible to calculate the optimised volume. Within the quasi-harmonic approximation, the Helmholtz free energy, A, is given by:
Equation 3
Where E0 is the internal energy, is the zero-point energy and is the entropic contribution.[3]
The computer model calculates the free energy by summing over the vibrations of the crystal. Each of these vibrations has a defined k value in reciprocal space and, for a monatomic chain, the vibrational frequency is:
Equation 4
This can then be extended to model a crystal lattice in three dimensions. A dispersion curve plots the vibrational frequencies in reciprocal space and therefore it is necessary to define the lattice parameter for reciprocal space, a*, as:
Equation 5
Molecular Dynamics Simulations
Molecular dynamics is a purely classical method for estimating the volume of an MgO crystal which involves repeatedly solving Newton’s equation of motion, , for the system. Each solution is for a small timestep and the solution of one timestep is always based on the result of the previous iteration. It should therefore be apparent that the size of the timestep will be key to the accuracy of a molecular dynamics simulation. The ideal timestep would be very long however, as previously seen, it is essential to consider the computing power required for such a calculation. A compromise between these two factors must be reached, and for this investigation, this was a time step of 1 fs.
A fundamental limitation of molecular dynamics simulations is the failure to consider quantum mechanical properties of the system. In particular the simulations do not account for the zero-point energy. Consequently, at low temperatures the results from molecular dynamics will be inaccurate.
Experimental
All calculations were carried out using DLVisualise as the Graphical User Interface with the molecular modelling code General Utility Lattice Programme (GULP). The pressure was set at the default (0 GPa) and Include Shells was not selected for all the calculations.
Computing Phonon Dispersion Modes
Phonon dispersion curves were calculated by computing the phonon frequencies along the path W-L-G-W-X-Y, at 300 K. Within the General Options section of the Execute GULP panel, Phonon Dispersion was selected, Npoints was set to 50, corresponding to calculating the phonon frequency at 50 points along the above path. Following file recovery, the phonon dispersion curve was visualised.
Computing Phonon Density of States
Phonon density of states (DOS) was calculated using the PhononDOS option within the Execute GULP panel, at a temperature of 300 K. The DOS was calculated with shrinking factors along the A, B and C directions all equal to 1 (a 1x1x1 grid) before calculating for larger grids corresponding to shrinking factors of 2, 3, 4, 5, 10, 16, 32 and 64. Following file recovery the phonon DOS curves were plotted.
Computing the free energy
Calculation of the free energy of a MgO crystal was included within the phonon DOS calculation and the value was extracted from the Log File. The free energy was identified for all the grid sizes listed above and the ideal grid size was chosen to minimise the computational time and power required whilst still maintaining a satisfactory level of accuracy in the result.
Thermal Expansion of MgO
The thermal expansion of MgO was investigated within both the quasi-harmonic approximation and with molecular dynamics. When using the quasi-harmonic approximation, the shrinking factors in the A, B and C directions were all set to 16, as had been found suitable from the previous part of this experiment. The temperature was then varied from 0K to 2900K. The volume of the primitive unit cell was identified from the Log File. This volume was converted to that of a conventional unit cell by multiplication by a factor of 4.
Molecular Dynamics calculations were then used to investigate the same features, thus allowing for comparison between models. Number of particles, pressure and temperature were fixed for each calculation by selecting NPT within the execute GULP panel. For all calculations the Time Step was set to 1 fs, equilibration and production steps set to 500 and sampling and trajectory write steps to 5. From the Log file the final optimised volume was identified, corresponding to the average value at 0.5 ps. As the molecular dynamics calculations were run on a supercell containing 32 MgO units, rather than the 4 in a conventional unit cell it was necessary to divide the outputted volume by 8 to get the conventional cell volume.
Results and Discussion
Phonon Dispersion and Density of States
When shrinking factors were all set to 1, the density of states is calculated for a 1x1x1 grid, corresponding to a single k point. Identifying this k point was done by analysing both the frequencies at which the peaks occurred and the density of the peaks.

Figure 2a shows the Phonon DOS plot. 2 peaks of equal density occur at 600-800 cm-1 region, whilst 2 with double this density show up at lower frequencies of around 200-400 cm-1. The higher density results from doubly degenerate states. Considering the phonon dispersion plot (figure 2b), it can be seen that at frequencies similar to both these DOS peaks, 2 band converge. The values of wavevector k at which this is observed is L. Using the Log File the exact values of frequency were found to be 288.49 cm-1 (doubly degenerate), 351.76 cm-1(doubly degenerate), 676.23 cm-1 and 818.82 cm-1.

By increasing the shrinking factor, the grid size is increased, consequently a larger number of k points are sampled and hence, as k is a wavevector, more of the systems properties can be elucidated.[4] The result is a DOS plot which far more accurately resembles reality. Rather than the plot of four distinct points in Figure 2a, for a 16x16x16 grid we see a detailed plot, containing most of the key features, the plot becomes yet more detailed when calculated for a 32x32x32 grid (figure 3b). On increasing the grid size further still, to a 64x64x64 grid, the plot changes little; indicating that a 32x32x32 grid provides a very reasonable approximation for the DOS. It is worth noting that calculation on a 64x64x64 grid takes a considerably greater amount of time than 32x32x32. Hence, the small gain in accuracy was not significant enough to calculate at the 64x64x64 level.
Free Energy Changes with Grid Size

The computational model used for these investigations calculates free energy by summing the vibrational modes of the MgO crystal over a finite number of k points, defined by grid size and consequently the shrinking factor. As a result, the accuracy of the calculation is extremely dependant on grid size, as is evident from the plot of free energy vs shrinking factor (figure 4).
The converged value is taken as that at which increasing the grid size causes no measurable change in the value of the free energy. Table 1 details the calculated free energy values for grid sizes varying from 1x1x1 to 64x64x64.
| Shrinking factor | Free Energy/ eV | Difference |
|---|---|---|
| 1 | -40.930301 | 0.003818 |
| 2 | -40.926609 | 0.000126 |
| 3 | -40.926432 | 5.1x10-5 |
| 4 | -40.92645 | 3.3x10-5 |
| 5 | -40.926463 | 2x10-5 |
| 6 | -40.926471 | 1.2x10-5 |
| 10 | -40.92648 | 3x10-6 |
| 16 | -40.926482 | 1x10-6 |
| 32 | -40.926483 | 0 |
| 64 | -40.926483 | 0 |
There is no change in the free energy on going from 32x32x32 to 64x64x64, therefore to 6 d.p. the free energy is -40.926483 eV. Using a 1x1x1 grid gives an inaccurate value for the free energy, 0.003818 different from the converged value. On the other hand, whilst the value of the free energy calculated for a 16x16x16 grid was not fully converged, it differed by just 1 meV. This was deemed accurate enough for the purposes of this investigation, and consequently the decision was taken to carry out all the calculations of free energy at temperatures between 0 K and 2900 K on a 16x16x16 grid so as to make most efficient use of computational power.
Considering other crystals
Whilst same computational techniques that have been used for MgO are also applicable to other lattice structures, they are not wholly transferable, and it is necessary to consider each structure individually. For similar structures like calcium oxide, also a group 2 metal oxide, which has a lattice parameter only 0.596 Å different to that of MgO[5] and therefore a similar lattice parameter in reciprocal space, a*, the shrinking factor most appropriate to MgO (16x16x16) will also give the desired level of accuracy for CaO. Unfortunately, this is not the case for faujasite, a zeolite mineral which has a much larger lattice parameter than MgO; 25.132 Å compared to 4.2072 Å for MgO. Given that the lattice parameter in reciprocal space has a reciprocal relationship to the parameter in real space (equation 5), faujasite will have a small reciprocal lattice parameter. As a result, a smaller grid size (and shrinking factor) will be adequate in order to accurately describe the key properties of the system (such as free energy).
In metals such as lithium strong metallic bonding leads to interatomic distances that are smaller than for oxides like MgO. The lattice parameter for lithium is 0.6972 Å smaller than MgO and consequently the lattice parameter in reciprocal space will be larger. Therefore, in order to accurately describe the key properties of a metallic system a greater number of k points would need to be sampled and hence a larger grid size should be used.
Thermal Expansion of MgO
The thermal expansion of MgO was modelled by considering lattice vibrations as quasi-harmonic as well as by using molecular dynamics.

Quasi-Harmonic
The quasi-harmonic model works best for low temperatures when vibrations only involve small displacements from equilibrium. Figure 5 shows the change in free energy as the temperature varies from 0 to 2900 K. When operating within the quasi-harmonic model it was not possible to investigate temperatures greater than 2900 K as the computer produced an error.
There are two distinct regions to this graph, an initial non-linear region between 0 K and ~1500 K, then a linear region above ~1500 K. This can be rationalised by considering the definition of the Helmholtz free energy:
Equation 6
Where A is the Helmholtz free energy, U is the internal energy, T is the temperature and S is the entropy.
The free energy will always decrease with temperature since both T and S are always positive. Were U and S to be temperature independent, this decrease would be perfectly linear, however they are not. As a result, for the initial section of the graph, when the temperature is relatively low, the variations in U and S with temperature are large enough to cause the free energy to have a non-linear temperature dependence. At high temperatures, these relatively small changes in U and S become insignificant in comparison to the change in temperature, to such an extent that we can take them to be constant. As a result, we see the free energy decrease linearly with temperature.
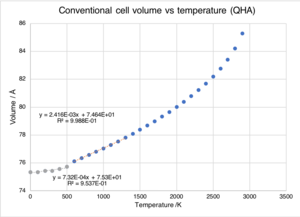
The quasi-harmonic model minimises the free energy in order to calculate the volume at a given temperature. Figure 6 shows a plot of optimised volume against temperature.
There is an initial linear region of the graph between 0 and 500 K. For this region, the thermal expansion coefficient, was calculated using equation 2 to be 9.715 x10-6 K-1 this is very close to the literature value for this temperature range which is 10.5 x10-6 K-1.[6] Between 600 K and 1300 K the plot shows that volume and temperature again have a linear relationship, for this region the thermal expansion coefficient was 31.7 x10-6 K-1. This is further from the literature value of 40 x10-6 K-1 than that calculated for the lower temperature region. The increase in the discrepancy between the experimental literature value and the calculated value is due to the failings of the quasi-harmonic approximation to account for bond dissociation and the considerable anharmonicity that occurs when approaching melting point (3125 K).[1] In the quasi-harmonic model, bond dissociation is not possible, and as a result at high temperatures, the calculated phonon modes do not accurately represent reality.
Molecular Dynamics
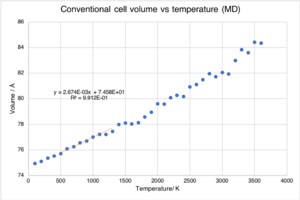
Figure 7 is the same plot as figure 6 except in this case the optimised volume has now been calculated using molecular dynamics.
The most significant difference between the two plots is that under the quasi-harmonic approximation the slope of the plot changed with temperature, whereas now it is constant. This is because molecular dynamics is purely classical and does not account for the zero-point energy. Consequently, at low temperatures when the zero-point energy is most significant, the results of the molecular dynamics simulations are highly inaccurate, and the calculated thermal expansion coefficient is the same as that for the higher temperature region (600 K to 1300 K).

The thermal expansion coefficient was calculated for the region 600 K to 1300 K to enable direct comparison to the value calculated within the quasi-harmonic approximation. It was found to be 35.2 x10-6 K-1, this is closer to the literature than the quasi-harmonic value; indicating that in this temperature range molecular dynamics gives a better model of the thermal expansion of MgO. At very high temperatures, approaching the melting point, the molecular dynamics simulation would be expected to more accurately describe the thermal expansion as it takes into account bond dissociation.[3] The calculated value of the thermal expansion coefficient in the region 2000 K to 3500 K was the same as that in the 600 K to 1300 K region due to the fully linear relationship.
Figures 8a and 8b are graphs of the lattice parameter against temperature, calculated with quasi-harmonics and molecular dynamics respectively. They show the same relation as plots of volume against temperature. This is expected since for a cubic conventional unit cell, like that of MgO, the lattice parameter is simply the cube root of the volume.
Conclusion
The thermal expansion of magnesium oxide has been modelled computationally within the quasi-harmonic approximation and with molecular dynamics. When using quasi-harmonics the optimal grid size was chosen so as to balance the need to accurately calculate free energy with that of minimising the computational power required; this optimal grid size was found to be a 16x16x16 grid. By modelling the volume changes with respect to temperature, the thermal expansion coefficient of MgO has been found as 31.7 x10-6 K-1 and 35.2 x10-6 K-1 in the region 600K to 1300K for quasi-harmonics and molecular dynamics respectively. Over this temperature range the value calculated by molecular dynamics was closest to the literature so it was concluded molecular dynamics modelled the system most accurately. This was not the case at lower temperatures where the failings of molecular dynamics to account for the zero point energy meant calculations were highly inaccurate. Here, quasi-harmonics provided a much better model, and the calculated thermal expansion coefficient was 9.72 x10-6 K-1.
Bibliography
- ↑ 1.0 1.1 III/17B-22A-41B, C. A. and editors of the volumes. II-VI and I-VII Compounds; Semimagnetic Compounds; Springer-Verlag: Berlin/Heidelberg; 1–6.
- ↑ Tipler, P. A.; Mosca, G. W H Freeman and Company: New York, 2003; 666–670.
- ↑ 3.0 3.1 3.2 Dove, M. T. Cambridge University Press: Cambridge, 1993.
- ↑ Hoffmann, R. Angew. Chemie-International Ed. English 1987,26 (9), 846–878.
- ↑ Doll, K.; Dolg, M.; Stoll, H. Phys. Rev. B - Condens. Matter Mater. Phys. 1996, 54 (19), 13529–13535.
- ↑ Sun, X. W.; Liu, Z. J.; Chen, Q. F.; Song, T.; Wang, C. W. Chinese Phys. B 2009, 18 (11), 5001–5007.
