Rep:Mod:ZhangWen

Introduction

The programme Gaussview was used to optimise all the molecules and was used to obtain the data presented below. The diagrams of MOs were also obtained using this programme.

NH3 Molecule

Optimisation

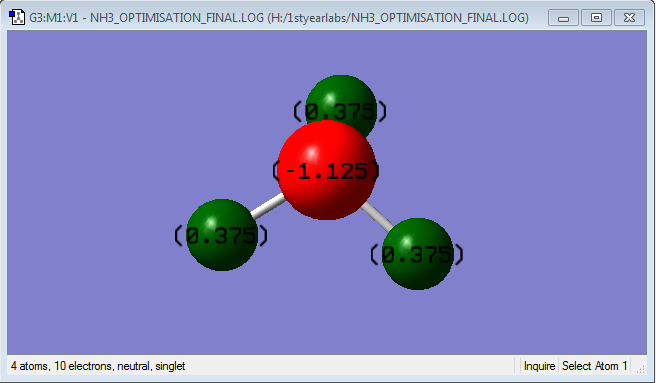
NH3 molecule

NH3 Bond Distance = 1.10798

NH3 Bond Angle = 105.741

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final energy E(RB3LYP) in atomic units (au): -56.55776873

RMS Gradient:

Point Group: C3V

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

The optimisation file is linked to here

Vibrations and charges

Vibrations

Using the 3N-6 Rule to calculate the number of modes expected, 3(4)-6 = 6, 6 modes are expected. Modes 2 and 3 are degenerate and modes 5 and 6 are degenerate as they have the exact same frequencies. Modes 4,5 and 6 are stretching vibrations, while modes 1,2 and 3 are bending vibrations. Mode 4 is highly symmetric and Mode 1 is also known as the umbrella vibration. In an experimental spectrum of ammonia, 2 bands are expected to be seen. Vibrational mode 1 involves a very large change in dipole moment, resulting in a very large intensity of the peak. Vibrational modes 4,5 and 6 involve a small cahnge in dipole moment, resulting in a very weak peak which cannot be seen. Hence only the peaks from vibrational mode 1, 2 and 3 can be seen on the spectrum and since modes 2 and 3 are degenerate, only 2 bands are seen on a infrared spectrum.

Charges

Nitrogen is expected to have a negative charge and Hydrogen is expected to have a positive charge. Since Nitrogen is more electronegative than Hydrogen, the electrons are more attracted to the nitrogen atom and, resulting in a higher electron density around it and hence a negative charge develops, while a positive charge develops for each hydrogen atom.

N₂ Molecule

Optimisation

N molecule

N₂ Bond Distance = 1.10424

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final energy E(RB3LYP) in atomic units (au): -109.52412868

RMS Gradient: 0.00000060

Point Group: D∞H

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 

The optimisation file is linked to here

Vibrations and charges

There will be no peaks as infrared spectroscopy only records vibrations which involve a change in its dipole moment. Since nitrogen exists as a homodiatomic molecule, a vibration would involve no change in its dipole moment and hence no peaks are seen. As nitrogen exists as a diatomic molecule with 2 nitrogen atoms with the same electronegativity, the charges on both atoms will be 0.

H₂ Molecule

Optimisation

H2 molecule

H₂ Bond Distance = 0.74249

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final energy E(RB3LYP) in atomic units (au): -1.17853936

RMS Gradient: 0.00000017

Point Group: D∞H

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

The optimisation file is linked to here

Vibrations and charges

The vibrational mode 1 has a very high frequency as a hydrogen molecule has a very small reduced mass. Furthermore, no peaks are seen due to the same reason as the nitrogen molecule above. As hydrogen is an homodiatomic molecule and both atoms have the same electronegativity, both atoms have a charge of 0.

Haber-Bosch Process

The Haber-Bosch process is used industrially to manufacture ammonia from atmospheric nitrogen gas and hydrogen gas. The reaction is done using a metal catalyst and is conducted under high temperatures and pressures. The Haber-Bosch process is the main industrial scale method is produce ammonia used today due to its efficiency.

To determine the energy for the reaction N₂ + H₂ --> NH₃, the following calculations are made:

E(NH₃)= -56.55776873au

2*E(NH₃)= -113.11553746au

E(N₂)= -109.52412868au

E(H₂)= -1.17853936au

3*E(H₂)= -3.53561808au

ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= -113.11553746 - [(-109.52412868) + (-3.53561808)] = -0.0557907au = -146.47849401kJ/mol

Since the energy difference is negative, the ammonia product is more stable than the gaseous reactants

HCL

Optimisation

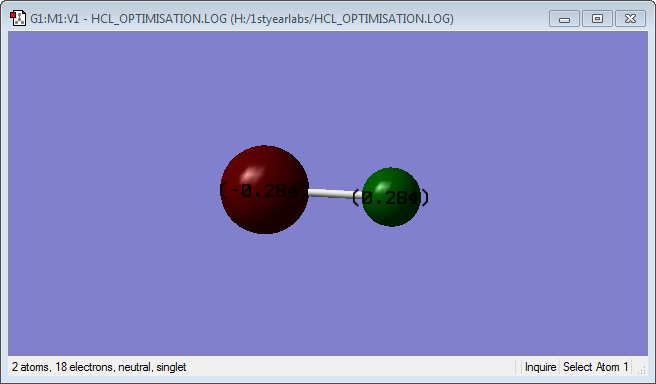
HCl molecule

HCl Bond Distance = 1.28599

HCl Bond Angle = 180

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

Final energy E(RB3LYP) in atomic units (au): -460.80077875

RMS Gradient: 0.00005211

Point Group: C∞V

         Item             Value        Threshold    Converged?
 Maximum Force            0.000090     0.000450     YES
 RMS     Force            0.000090     0.000300     YES
 Maximum Displacement     0.000139     0.001800     YES
 RMS     Displacement     0.000197     0.001200     YES

The optimisation file is linked to here

Vibrations and charges

Vibrations

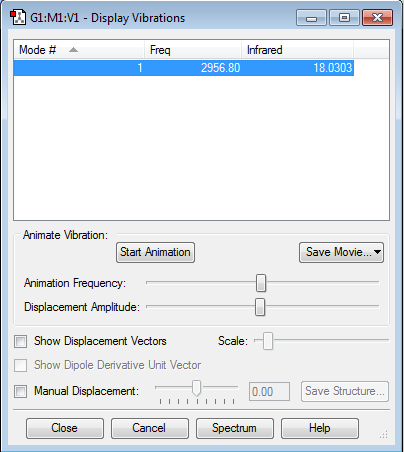
For linear molecules, using the 3N-5 rule, one vibrational mode is expected. The vibrational mode is a stretching vibration.

Charges

Since Chlorine is more electronegative than hydrogen, the shared electrons are pulled towards the chlorine resulting in a higher electron density around the chlorine atom as compared to the hydrogen. Hence a partial negative charge and a partial positive charge develops around the chlorine and the hydrogen respectively.

Molecular Orbitals

Molecular Orbitals	Description
	Energy: - 0.84773. This is a non-bonding MO from the 3s atomic orbital of chlorine. There is a very small contribution to the MO from the hydrogen 1s AO as the MO produced is not completely spherical. The MO is completely filled with the 2 electrons from chlorine. The MO is also relatively low in energy and not in the HOMO and LUMO region.
	Energy: -0.47433. This is a bonding molecular orbital between the 1s AO of hydrogen and the 3p AO of chlorine. The MO is fully occupied with one electron from the chlorine and one electron from the hydrogen. The MO is low in energy due to the stabilisation of the AOs as they combine in-phase.
	Energy: -0.33163. This is a non-bonding MO from the 3p AO of chlorine. The MO is completely filled with the 2 electrons from chlorine. The MO is higher in energy than the non-bonding MO from the 3s AO of chlorine. This is due to the 3s orbital being able to penetrate and get closer to the nucleus, hence it becomes stabilised more and is lower in energy. The MO is the HOMO.
	Energy: -0.33163. This is also a non-bonding MO from the 3p AO of chlorine and is degenerate with the orbital mentioned above.
	Energy: -0.01366. This is the anti-bonding MO from the 3p AO or chlorine and the 1s AO of hydrogen. The MO is unoccupied, high in energy and is the LUMO.