Rep:Mod:ZQHMod3

In this module, the computational technique would be used to calculate the transition states of the reaction: the Cope rearrangement and Dields-Alder Cycloaddition. The geometry structure of the transition state will be found and so the corresponding low energy product.

The Cope rearrangement

Optimisation of 1,5 hexadiene Because of the free rotation of the C-C single bonds in the centre of the molecule, there are several possible structures for the molecule. They are 6 guache and 4 anti-periplanar conformers as lists in the Appendix 1 table. The molecules are drawn with Gaussian View 5. The different conformers are obtained by manually adjusting the dihedral angles of the molecule. Then they are “cleaned” by using the clean under Edit menu, followed by optimisation (HF/3-21G) with %memory = 250MB. After optimisation, the point group of the conformers are obtained by Symmetrize under the Edit menu.

Conformer	Energy	Point Group	Geometry
anti1	−231.692602 a.u.	C2	Media:anti1 opt zqh.ogg
anti2	−231.692535 a.u.	Ci	Media:anti2 opt zqh.ogg
anti3	−231.689071 a.u.	C2h	Media:anti3 opt zqh.ogg
anti4	−231.690971 a.u.	C1	Media:anti4 opt zqh.ogg
guache1	−231.687716 a.u.	C2	Media:guache1 opt zqh.ogg
guache2	−231.691667 a.u.	C2	Media:guache2 opt zqh.ogg
guache3	−231.692661 a.u.	C1	Media:guache3 opt zqh.ogg
guache4	−231.691530 a.u.	C2	Media:guache4 opt zqh.ogg
guache5	−231.689616 a.u.	C1	Media:guache5 opt zqh.ogg
guache6	−231.689160 a.u.	C1	Media:guache6 opt zqh.ogg

From the table above, the anti1, anti2 and guache3 are the most stable structures. They are optimised with B3LYP/DFT/6-31G(d) setup. Guache3 is the most stable one from the table above.

Conformer	Energy	Point Group	Geometry
anti1	−234.61276 a.u.	C2	Media:anti1 opt 631g zqh.ogg
anti2	−234.61267 a.u.	Ci	Media:anti2 opt 631g zqh.ogg
guache3	−234.61230 a.u.	C1	Media:guache3 opt 631g zqh.ogg

The new results of the three structures from higher level basis are lower than the previous ones. All the minimum energy values are about 3 a.u. lower. The anti1 conformer is the most stable one while guache3 is the least one, which is different from the previous order. The reason for anti1 is the most stable conformer is the best overlap between σ C-H and σ* C(3)-C(4) orbital.

Frequency Analysis

The frequency analysis of the three conformers are run from the optimised B3LYP/DFT/6-31G(d) structures. The low frequencies below shows the optimisation of the conformers is successful.

Anti1

Low frequencies ---   -9.2657   -5.2822   -0.0004    0.0004    0.0005   23.6509
Low frequencies ---   73.2248   96.1113  113.5387

Anti2

Low frequencies ---  -13.8019   -8.9932   -0.0004   -0.0001    0.0001    3.5924
Low frequencies ---   71.6349   78.0954  116.2414

Guache3

Low frequencies ---   -7.0386   -3.6641   -0.0006   -0.0004   -0.0002    9.9938
Low frequencies ---   71.8472   98.9932  122.3847

The table shows the C=C symmetric and asymmetric stretch frequencies. The symmetric stretches of the two anti conformers have a low intensity due to the high symmetry of the conformer. They belong to a high symmetry point group. The guache3 belongs to a low symmetry group, so both of the symmetric and asymmetric stretches have a higher intensity values.

Conformer	Frequency	Intencity	.gif		Frequency	Intencity	.gif
anti1	1698	6.96		Symmetric C=C stretch	1701	19.47		Asymmetric C=C stretch
anti2	1698	0		Symmetric C=C stretch	1701	26.42		Asymmetric C=C stretch
guache3	1699	9.55		Symmetric C=C stretch	1700	10.96		Asymmetric C=C stretch

Thermochemical data

The data are from the .log files of the vibration analysis.

The meanings of the terms are

1 the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE)

2 the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans)

3 the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions,

4 the last includes the entropic contribution to the free energy (G = H - TS)

Each type of the energies of anti1 conformer is the lowest among the three structures. The energy values of anti2 are close to anti1, but for guache3, the energy differences are more.

Anti1

Sum of electronic and zero-point Energies=           -234.470413
Sum of electronic and thermal Energies=              -234.463138
Sum of electronic and thermal Enthalpies=            -234.462194
Sum of electronic and thermal Free Energies=         -234.501319

Anti2

Sum of electronic and zero-point Energies=           -234.470332
Sum of electronic and thermal Energies=              -234.463025
Sum of electronic and thermal Enthalpies=            -234.462081
Sum of electronic and thermal Free Energies=         -234.501962

Guache3

Sum of electronic and zero-point Energies=           -234.469842
Sum of electronic and thermal Energies=              -234.462653
Sum of electronic and thermal Enthalpies=            -234.461709
Sum of electronic and thermal Free Energies=         -234.501306

Optimisation of Transition states

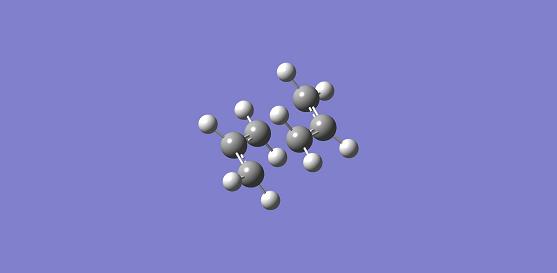
Optimise Chair TS with Computing the Force Constant Matrix

An allyl fragment (CH2CHCH2) is drawn and optimised with HF/3-21G basis. The fragment is then copied with Append Molecule function so two allyl fragments are in one molecules window. The two fragments are 2.2A apart.

Opt+Freq and Optimization to a TS (Berny) are selected. Basis setup is HF/3-21G. The calculation will be done once. Additional keyword is Opt=NoEigen. With these setup, the optimised structure of the Chair TS is found.

Frequency	Intensity	Energy	.gif
−818	5.91	−231.61932 a.u.

Optimise Chair TS with Freezing Reaction Coordinates

The distance apart from the two terminal carbon pairs of the two fragment are fixed as 2.2A by Redundant Coord Editor under the Edit menu. The optimisation is done to find the minimum energy geometry with HF/3-21G. Then with setup Opt+Freq, Optimization to a TS(Berny) and HF/3-21G, the pre-optimised .chk file is optimised with fixed bond length.

Frequency	Intensity	Energy	.gif
−818	5.85	−231.61932 a.u.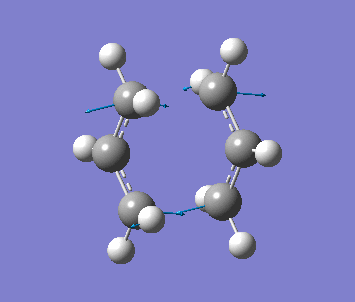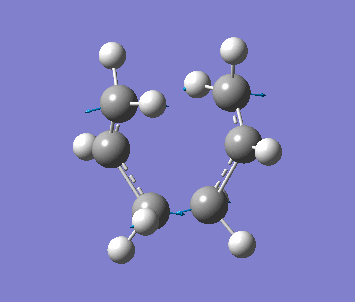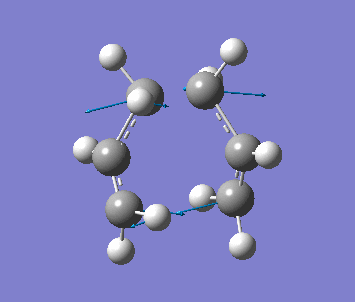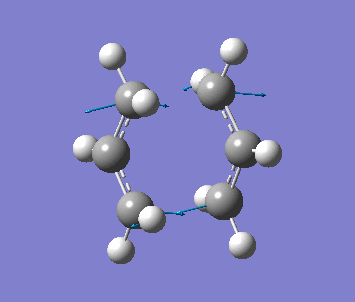

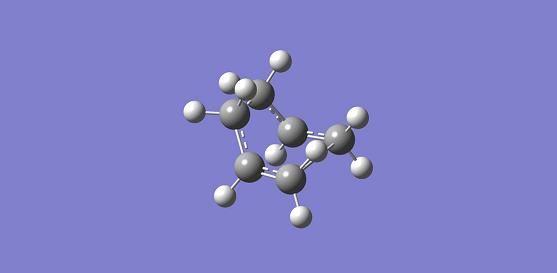
Optimising the Boat TS with QST2 method

Firstly, two anti2 conformer molecules are added into one molecule window and the carbon atoms of the 2 molecules are labeled by using the Atom List under Edit menu, as one is reactant, the other is product. The molecule is optimised with Opt+Freq, TS(QST2) and HF/3-21G with additional keywords, Opt=NoEigen. The optimisation is failed since the structures of the molecules are chair form.

The structure is then manually adjusted. The dihedral angle of C2-C3-C4-C5 is change to 0 degree, and the bond angle C2-C3-C4 and C3-C4-C5 are changed to 100 degree for the reactant molecule. Then for the product molecule, same thing is done. The new structure is sent to optimise again to obtain a successful optimised structure.

Frequency	Intensity	Energy	.gif
−840	1.64	−231.60280 a.u.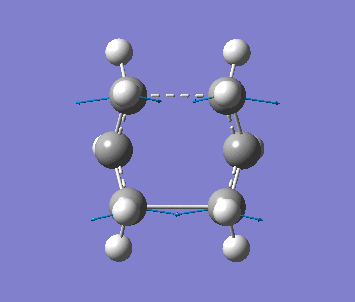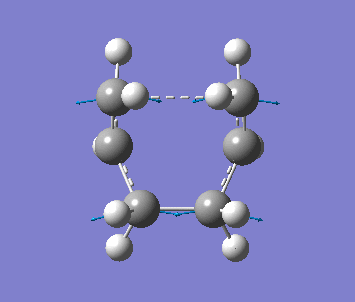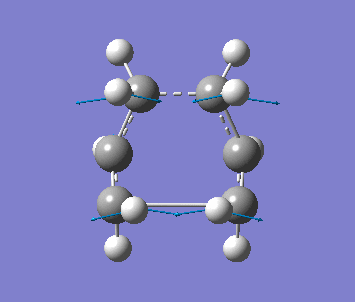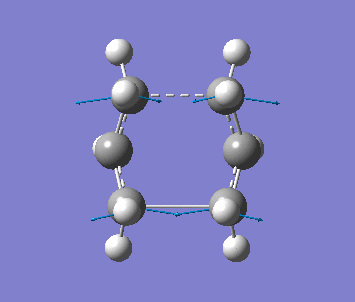

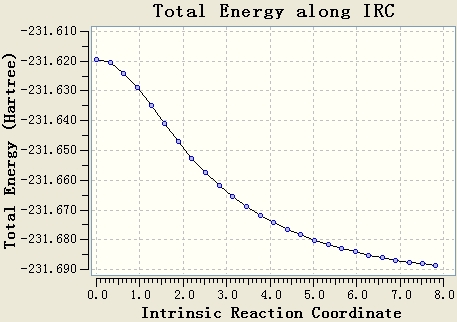
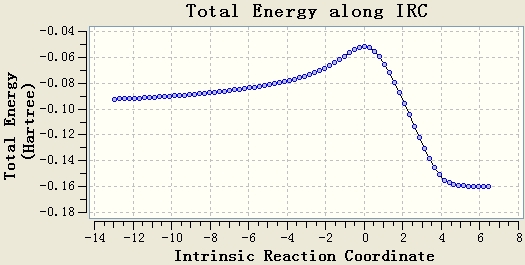
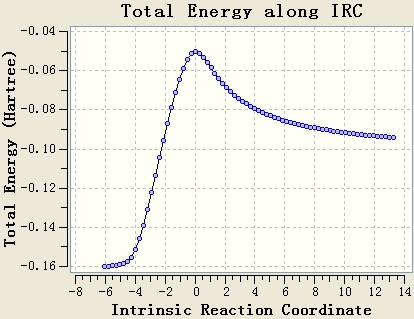
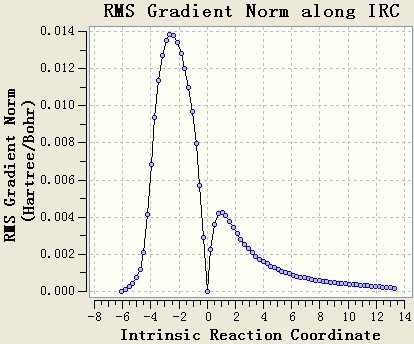
Intrinsic Reaction Coordinate

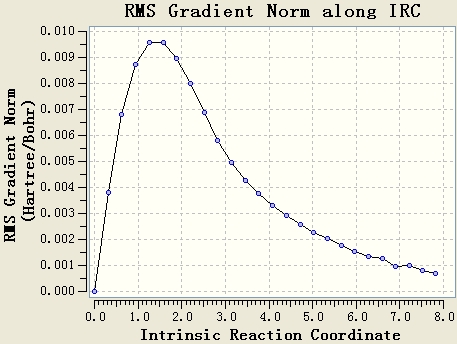
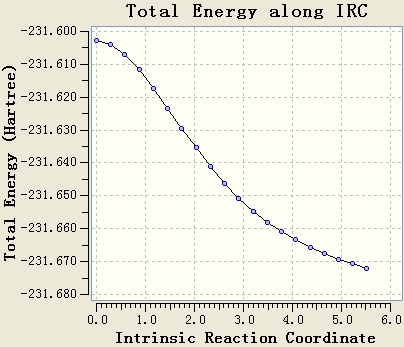
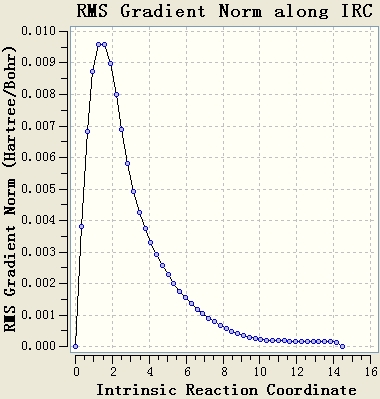
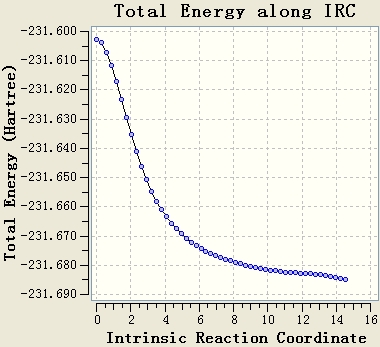
The IRC calculation is done with the setups IRC, HF/3-21G, maximum steps=50 and force constant will be calculated once. The resultant table shows that the optimisation is not end at a minimum energy state, since the gradient of the energy curve at the end is not 0.

Chair transition state results. Energy = -231.61932 a.u..

Boat transition state results. Energy = -231.60280 a.u..

The original IRC optimisation stops at 23 steps, so increasing the number of steps and re-run the IRC are meaningful. This will work if the maximum 50 steps is not enough.

Re-run the IRC with force constants calculated at each step is a good method. From the table, it can be seen that the gradient of the energy curve at the end is 0. So the geometry is optimised well.

Chair transition state results. Energy = -231.61932 a.u..

Boat transition state results. Energy = -231.60280 a.u..

The final IRC is done to give the following structure.

Activation energy

The activation energy of the cope rearrangement is calculated with two different bases, HF/3-21G, and B3LYP/631G(d). The activation energy is obtained by subtract the reactant energy from the transition state energy. Since the lowest energy conformer of the two bases is different, the reactant conformer used is different.

Basis	Reactant energy	Chair TS energy	Boat TS energy	Activation energy to Chair TS	Activation energy to Boat TS	Conformer chosen
HF/3−21G	−231.69266 a.u.	−231.61932 a.u.	−231.60280 a.u.	0.07334 a.u.	0.08986 a.u.	Guache3
B3LYP/6−31G(d)	−234.61276 a.u.	−234.42750 a.u.	−234.54639 a.u.	0.18526 a.u.	0.06637 a.u.	Anti1

The results from the two diferent basis are opposite. The 6-31G(d) basis suggests that the activation energy of boat structure is smaller which is unexpected. Also 6-31G(d) is a higher basis. From the results of 3-21G basis, it can be seen that the activation energy of boat TS is larger than that of chair TS, so the chair TS is kinetic favoured.

Conclusion

From the above analysis, the guache3 conformer and the anti1 conformer are the most stable conformers. It depends on the basis used. The activation energy of chair TS is lower than that of boat TS, so the chair TS is the major under kinetic condition.

The Diels-Alder Cycloaddition

Optimisation of Ethene and Butadiene

The reactants, ethene and butadiene, are drawn with Gaussian View and then optimised with AM1 method.

Reactants	LUMO	HOMO	Energy
Ethene	a	s	0.026190 a. u.
cis-Butadiene	s	a	0.048797 a. u.

Orbital symmetry is very important in cycloaddition reaction. It can be seen from the table easily that the HOMO of ethene is s and LUMO of cis-butadiene is a. Also LUMO of ethene is a and HOMO of cis-butadiene is s. So the cycloaddition reaction is allowed.

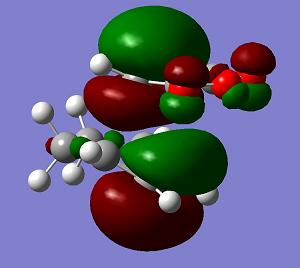
Optimisation of Transition states

The transition state of the reaction is optimised by using the freezing coordinate method. The basis set used is AM1. The guess structure of the transition state is from the figure below. The guessed distance between the bonding atoms are 2.09A.

LUMO	HOMO	HOMO−1	Energy	.gif	Frequency
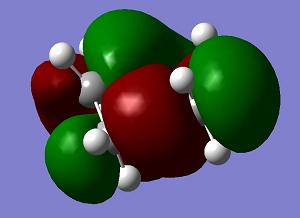
			0.20111 a. u.		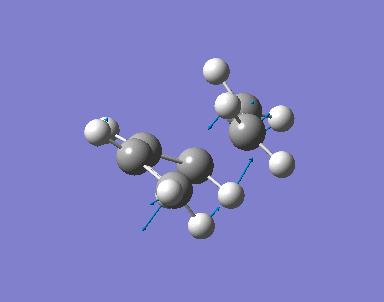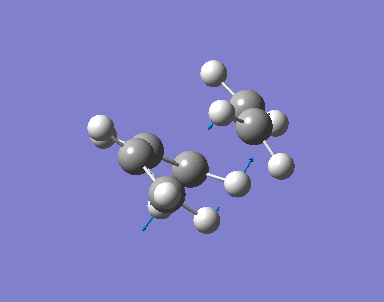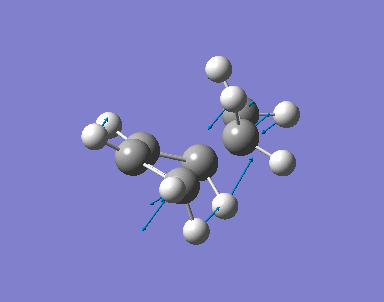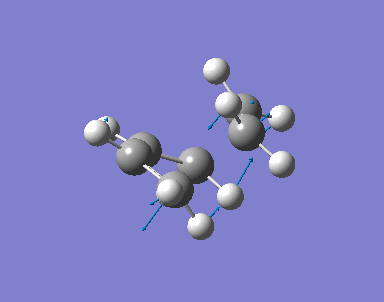−944

The LUMO and HOMO-1 of the transition state are symmetric, and the HOMO of the transition state is asymmetric. The energies of HOMO and HOMO-1 are very close. Though HOMO is an anti bonding orbital, the structure is stabilised.

Intrinsic Reaction Coordinate

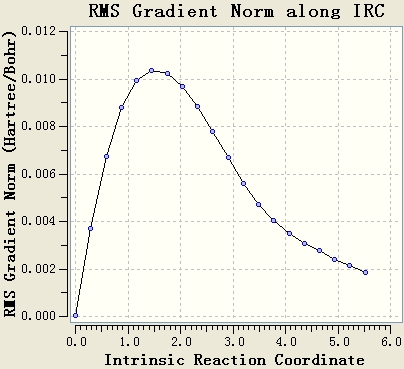
The IRC is done by using AM1 basis. The force constant is calculated at every step and both directions are calculated.

The gradients of curves of both directions are very close to 0. The optimised transition state is at low energy level.

Optimisation of Cyclohexadiene and Maleic Anhydride

The reactants, Cyclohexadiene and Maleic Anhydride, are drawn with Gaussian View and then optimised with AM1 method.

Reactants	LUMO	HOMO	Energy
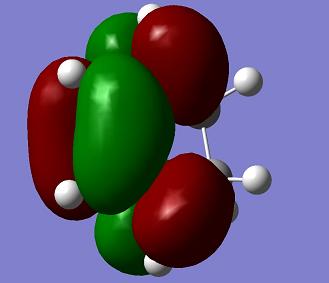
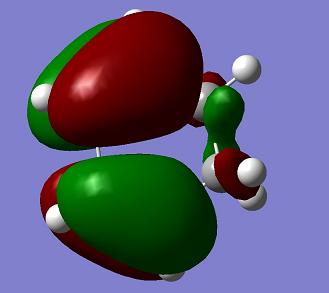
Cyclohexadiene	s	a	0.027711 a. u.
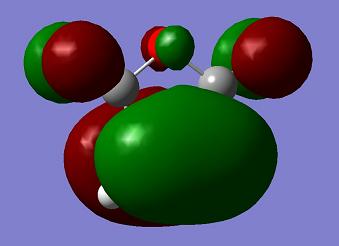
Maleic Anhydride	a	s	−0.12182 a. u.

The orbital symmetry of the two reactants is like the previous case. The HOMO of maleic anhydride and LUMO of cyclohexadiene are the same symmetry and so are the LUMO of maleic anhydride and HOMO of cyclohexadiene.

Optimisation of Transition states

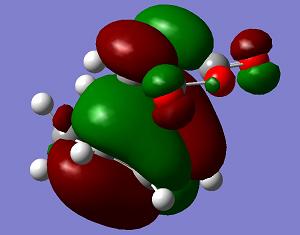
The transition state of the reaction is optimised by using the freezing coordinate method. The basis set used is AM1. Due to the repulsion from the (O=C)-C-(C=O) fragement and the CH2-CH2 or two alkene fragments, the guessed structure need to be adjusted manually. Otherwise the optimisation will fail and no product forms. For the exo product, the dihedral angles of cyclohexadiene are set to be -12.8 for C=C-C=C and ±35.9 for two C-C=C-C, the bonding atoms distances starts from 2.4-2.6A and are fixed at 2.09A. For the endo product, since the repulsion is much smaller, the distance between bonding atoms are from 2.10-2.11 and are fixed at 2.09A. No dihedral angle needs to be changed.

LUMO+1	LUMO	HOMO	HOMO−1	Energy	.gif	Frequency
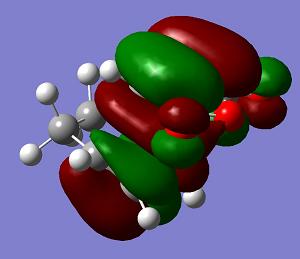
s	a	s	a	−0.051505 a. u.		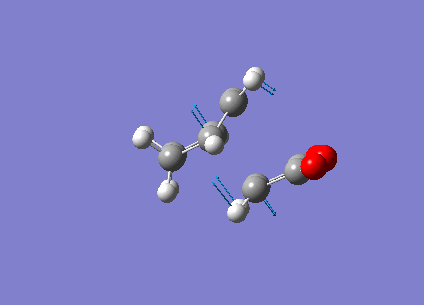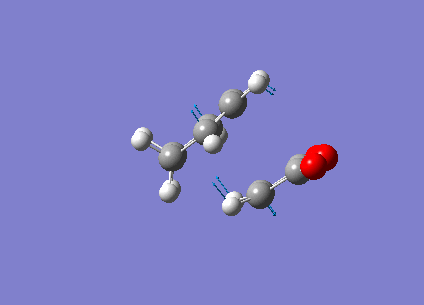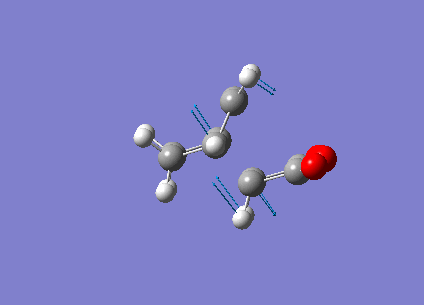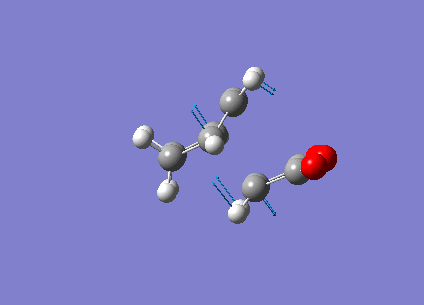−860

LUMO+1	LUMO	HOMO	HOMO−1	Energy	.gif	Frequency
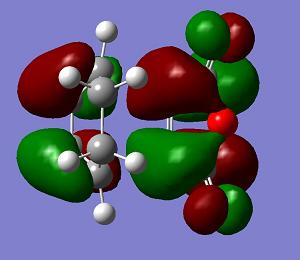
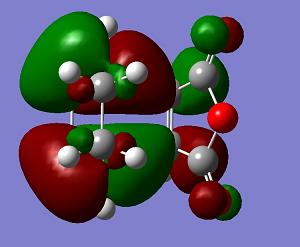
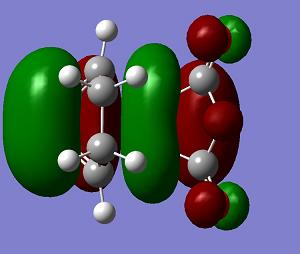
s	a	a	s	−0.050420 a. u.		−812

The endo transition state structure has a lower energy than that of exo as expected. The endo product is the major at low temperature, since the energy gap between the transition state and reactant is smaller. The endo product is kinetic favoured. The orbitals of the exo and endo transition states are similar. Only LUMO+1 shows a difference. So the difference in energy is due to the steric effect as mentioned.

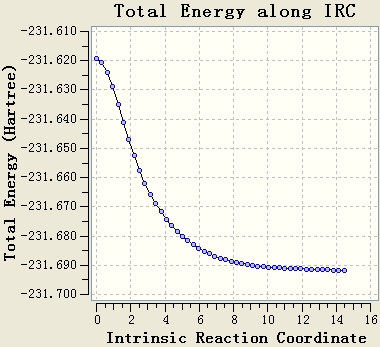
Intrinsic Reaction Coordinate

The IRC is done by using AM1 basis. The force constant is calculated at every step and both directions are calculated. Both the IRCs give good results with the gradients of energy curves being close to 0.

Discussion

Bond length

Bond Type	C-C	C=C	forming C-C	Typical C-C	Typical C=C
Bond Length	1.39A	1.38A	2.09A	1.54A	1.34A

Bond Type	C=C in cyclohexadiene	C-C in cyclohexadiene	C=C in Maleic anhydride	forming bond	Transition state	Typical C-C bond	Typical C=C bond
Bond Length	1.39A	1.40A	1.41A	2.16A	Endo	1.54A	1.34A
Bond Length	1.39A	1.39A	1.41A	2.17A	Exo	1.54A	1.34A

From the bond length listed in the table, the forming bond of transition state structure is longer than the typical C-C bond, which is 1.54A. The C=C bonds of the transition states are also longer, since the typical C=C bond length is 1.34A. The longer forming bond length suggests that the interaction is attractive. The two reactant molecules coming together and form the product. The longer C=C bond length indicates that the delocalisation of electron density. The C-C bond length is shorter than the typical C-C bond length and is nearly the same length as the C=C bond. In the transition state, the C=C bonds and C-C bonds are in a situation between forming and breaking.

Compare the endo and exo transition states, the bond length of formed bonds are nearly same, but the bond length of forming bonds are a little different. That of endo structure is shorter, so the endo structure is favourable. It is closer to the typical C-C bond length.

Activation energy

Basis	Reactant energy	Endo TS energy	Exo TS energy	Activation energy to Endo TS	Activation energy to Exo TS
AM1	−0.09411 a. u.	−0.05150 a. u.	−0.05042 a. u.	0.04261 a. u.	0.04369 a. u.

The activation energy of endo structure is lower than that of exo structure, so endo structure is kinetic favoured.

Conclusion

From the optimisation of the reactants, the symmetry of the orbitals allows the reaction to take place. The HOMO of one reactant has the same symmetry as the LUMO of the other reactant.

For both of the reactions, the forming bond length of the transition states indicates the attractive reaction. The endo structure has a lower energy level and so lower activation energy. It is the kinetic favoured route. The reason for this is mainly due to the repulsion between CH2-CH2 and O=C-C-C=O fragments during the approach of the two reactant while form the exo TS.

Conclusion

From the analysis above, the computational technique can predict the transition state of simple reactions. For complex reactions, higher basis set will be used and stronger computer power is needed. The guessed transition state structure is very important. A good starting point will save much resource during the calculation of correct transition states and their energies.