Rep:Mod:ZG1413 Transition States
Pericyclic reactions have two distinguishing features, those being: a cyclic transition state and concerted mechanism.[1] Numerous synthesis routes to valuable organic compounds require pericyclic reactions, which makes this class of reactions invaluable; an example of which is the synthesis of adamantine, where the cycloaddition of cyclopentadiene affords dicyclopentadiene, which is then reduced to adamantine.[2] Understanding how these reactions evolve, and the factors that affect them is not only of academic interest, but also important in evaluating new synthetic routes to desired compounds. This computational experiment aims to investigate conformational minimum of1,5-hexadien for the Cope rearrangement, and to explore the most plausible transition state for this reaction and two Diels-Alder cycloadditions. A short description of pericyclic reactions, transition states and computational techniques is outlined below, with more information being provided in a prelude of each section.
A set of rules, known as the Woodward-Hoffman rules, describes the requirements for allowed pericyclic process. If the energy barrier, also known as the transition state, is too high and orbital symmetry is not conserved, then the pericyclic reaction will not proceed; low energy barriers and conservation of orbital symmetry are required for a successful pericyclic reaction. Equation 1 describes the requirements for thermally allowed pericyclic reactions; where n and q are integers, and s and a stands for suprafacial and antarafacial, respectively. For photochemically allowed pericyclic reactions, the summation of the electronic terms must equal an even number instead of odd.[3]
(1)
Transition state structures are defined by energy maxima on a reaction coordinate between reactants and products. By virtue of their energy maxima, these species are regarded transient, and observing them experimentally is extremely difficult; recent advancements however have permitted observations to become a reality. Therefore, to elucidate these species and acquire an understand of the underpinning chemistry, a different approach is generally adopted. Hammond's postulate and computational techniques are employed instead to determine the energy of guessed transition state structures. Hence, permitting plausible mechanisms to be verified and an understanding of the underlying chemistry to be gained. Hammond's postulate states that a transition state structure shall represent the species of the reaction that it is closest in energy to.[4] Therefore, for an exothermic process, the transition state should resemble the reactants more than the products. The change in Gibbs free energy of a reaction tends to be known, so it is possible to propose plausible structures for transition state structures. Calculating the energy of each feasible structure, with computational techniques, can determine which one is the most stable, and therefore, more likely to occur.
It was previously stated that, to understand pericyclic reactions further, more information regarding their transition states must be elucidated. As pericyclic reactions proceed in a concerted manner, with a cyclic transition structure, it is possible to guess a structure and probe their plausibility. These constraints for pericyclic reactions makes it relatively easy to guess a small number of transitions structures. Computational methods are then required to numerically solve the Shrodinger equation, seen in equation 2, with some assumptions that simplify the calculation, owing to the fact that solving the equation for a many-body system is physical impossible as separation of variables can not be achieved. One of the main assumptions that is employ is the Born-Oppenheimer Approximation, which assumes that the nuclear and electronic wave functions can be separated, as the nuclear and electronic motion occurs on completely different time scales.[5] Thereby, permitting potential energy surfaces to be obtained from parameterisation of the electronic wavefunction. Different computational approaches have varying degrees of approximations, most of which alter the basis set used, which results in stark inconsistencies.
(2)
Two types of ab initio calculations (which determine parameters from first principles) and semi-empirical calculations were utilised in this report.[5] Namely the Hartree-Fock (HF) method and density functional theory (DFT) were the employed ab initio calculations. In these calculations, it is assumed that electron-electron interactions are ignored, and instead, each electron experiences a constant potential. Hartree-Fock (HF) is regarded as one of the simplest methods employed in computational chemistry. Where it is also assumed that linear combination of atomic orbitals is valid in order to parameterise the electronic wavefunction using variational theorem. Parameterisation is iteratively performed, with the variational principle, until a value of the energy as close to the actual is obtained. Density functional theory (DFT) describes systems through electron density functionals (functions of functions). Semi-empirical calculations are based on HF, with some empirical parameters, and additional assumptions to simplify the calculation. Hence, these calculations tend to be less computationally expensive than HF.[5]
All of the methods described above required a basis set for the calculations. Basis sets refer to a collection of atomic orbitals (AO), which are centered at atomic sites, used in the calculation to describe the energy and bonding. Core orbitals tend to be neglected in the basis set, owing to the fact they contribute very little, if at all, to the bonding, and therefore energy. Furthermore, neglecting some of the orbitals reduces the number of calculations that need to be performed.
Nf710 (talk) 16:47, 25 February 2016 (UTC) excellent intro. Your mechanistic understanding is excellent. Your understanding of the methods could possibly be more detailed but you have the correct idea and seem to understand the variation principle so well done!
Cope Rearrangement
Optimisation of 1,5-hexadiene, to determine its energy, in several different conformations permitted the global minimum to be explored. Discussion of which conformation may actually be the global minimum, with reference to literature, was then undertaken. Two guess transition states were constructed and optimised using numerous different techniques to determine the most plausible structure. These two sets of calculations permitted the activation energy of the Cope rearrangement to be approximated, and in the process, the underlying mechanism revealed.
Arthur Cope developed thermal [3,3]-sigmatropic rearrangements of 1,5-dienes in 1940.[6] Sigmatropic reactions are governed by the Woodward-Hoffman rules, which are described in equation 1 of the previous section, and are distinguished from other pericyclic reactions by the fact that the overall number of and bonds remains unchanged; in other pericyclic reactions, such as cycloaddition and electrocyclic, the number of and change.[7] For the [3,3]-sigmatropic reaction to be thermally available, the components must either combine in a suprafacial/suprafacial or antarafacial/antarafacial manner; of course, by deduction, the photochemically allowed reaction can only proceed by suprafacial/antarafacial. It is assumed, in this report, that the Cope reaction is being driven thermally; therefore, the guessed transition structures incorporate this selection.
Above is the reaction scheme for the Cope rearrangement. Without numbering of carbon atoms, it would appear as if no overall change in the compound has occurred. This is, in fact, true for this example, but the reaction is known to occur nonetheless. Furthermore, there are derivatives of the Cope rearrangement, such as the Oxy-Cope, that do not exhibit reversible rearrangement because of enthalpy reasons. Studying 1,5-hexadiene is greatly simplified for this reason.
Optimisation of 1,5-Hexadiene
There are 27 conformations of 1,5-hexadiene from free rotation about three CC bonds. Not all of these conformation are distinct, however; symmetry of 1,5-hexadiene results in only 10 of these being energetically distinct. In the search of a global minimum for 1,5-hexadiene, several conformations can be neglected, as it is intuitively evident that these are not going to have a low energy. Gung et al. conducted a study which shall form the basis for investigating the conformational global minimum at the HF/3-21G and B3LYP/6-31G(d) basis set.[8]
HF/3-21G and B3LYP/6-31G(d) optimisations of the minimum and frequency were the calculation methods used in the following sections.
Optimisation of Antiperiplaner 1,5-Hexadiene
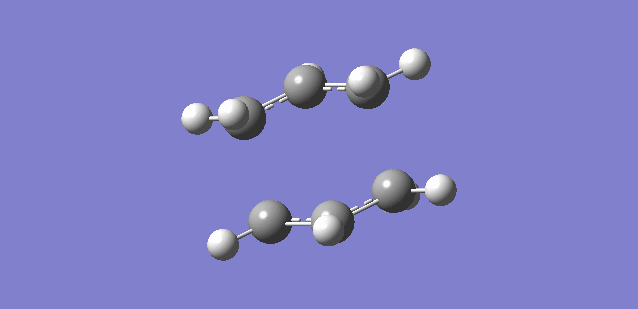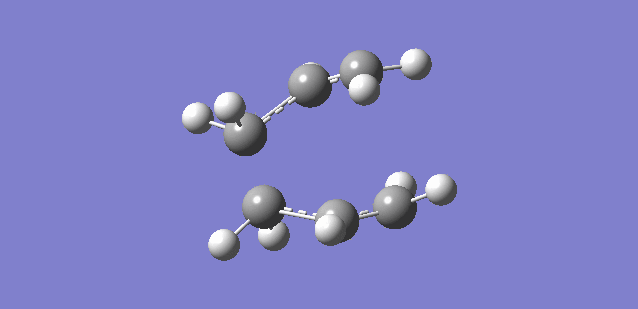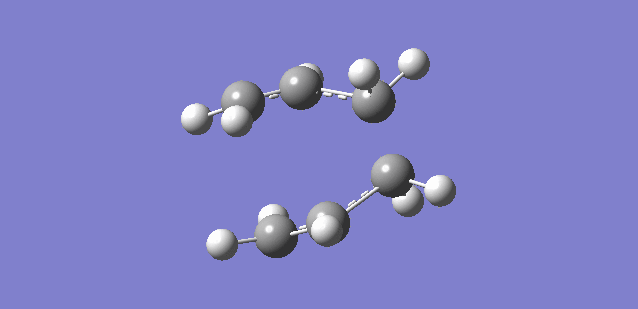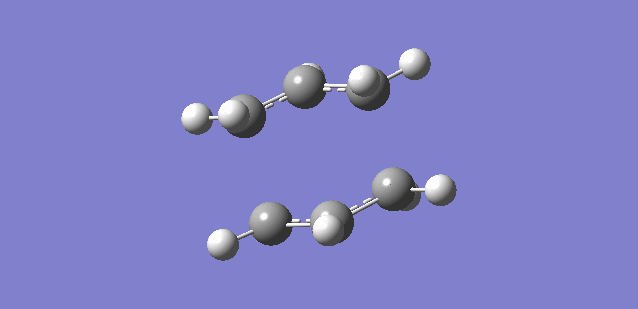
Antiperiplanar 1,5-hexadiene was constructed and optimised at the HF/3-21G level. Upon inspection of the optimised 1,5-hexadiene, which can be seen in figure 2, it was evident that it possessed the same structure and symmetry () as conformation anti2 in appendix 1. An energy of -231.69253528 Hartrees was obtained, which was essentially the same as that seen for anti2 in appendix 1. Stating energy values for 11 significant figures is, of course, completely absurd, but has been used to highlight slight variations from the appendix and confirm their authenticity. These slight variations arise because of the intrinsic nature of numerical calculations, which have a small associated error.
| Figure 2. Antiperiplaner 1,5-hexadiene optimised at HF/3-21G. |
Table 1 displays the obtained thermochemical data, for the HF/3-21G level, at standard temperature (298.15 K), close to zero (0.01 K) and at a high temperature (400 K). It should be noted that a temperature of 0 K was not be attempted, owing to the fact that Gaussian produces and error. As expected, the contribution to the energy from thermal sources has disappeared and an increased contribution is observed at higher temperatures. To change the temperature, an additional line was required in the keywords before submitting the Frequency calculation, those words being: genchk temperature=0.01.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 1. Summary of obtained thermochemical data at different temperatures for the HF/3-21G level. | |||
Optimisation of antiperiplanar 1,5-hexadiene from the previously optimised structure (at the HF/3-21G level) with the B3LYP/6-31G(d) level was undertaken. Figure 3 displays the obtained conformation. As expected, a large discrepancy between the energy of 1,5-hexdiene calculated with different basis sets was observed; B3LYP/6-31G(d) calculated the energy to be -234.61170280 Hartrees, which is significantly lower than that of the HF/3-21G level. Again a point group of was obtained for this conformation.
| Figure 3. Antiperiplaner 1,5-hexadiene optimised atB3LYP/6-31G(d) level. |
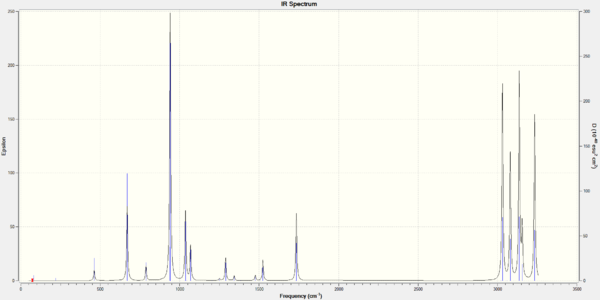
No negative frequencies of vibration were observed in the table of wavenumbers from the B3LYP/6-31G(d) frequency calculation. Figure 4 displays the calculated IR spectrum for this conformation.
Table 2, seen below, displays the obtained energy values from performing Frequency calculations at the B3LYP/6-31G(d) level for the same temperatures as previously investigated. The obtained values displayed in table 2 are in agreement with those displayed in summary of energies of appendix 2.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 2. Summary of obtained thermochemical data at different temperatures for the B3LYP/6-31G(d) level. | |||
A visual inspection of the conformation calculated at the two different levels, seen in figures 2 and 3, was undertaken and essentially no were differences found. Hence, the tools available were utilised to quantitatively investigate any differences. Slight variations in CC bond distances and dihedral angles were noticed; table 3 summarises the obtained measurements. These differences do not seem to be significant, however.
| Bond | HF/3-21G CC Bond lengths / nm | B3LYP/6-31G(d) CC Bond lengths / nm | Experimental CC Bond lengths / nm |
|---|---|---|---|
| Vinyl | 1.31613 | 1.33352 | 1.340 |
| Allyl | 1.50891 | 1.50419 | 1.508 |
| Central | 1.55275 | 1.54814 | 1.538 |
| Table 3. Summary of obtained CC bond distances and those from experiment.[9] | |||
Dihedral angles for the central bond and allyl bonds were measured. The central dihedral angle was found to have the angle expected for an antiperiplanar conformation. Measurements for the allyl carbons were also taken for the HF/3-21G and B3LYP/6-31G(d) level, which were fond to have values of 114.669 and 118.528, respectively. It would be expected that a dihedral angle close to 120 would be obtained. There is a balance between steric congestion and stabilising stereoelectronic interactions for this dihedral angle. Increasing the dihedral angle favours the reduction of repulsion, but disfavours the orbital overlap between the orbital and .
A comparison to electron diffraction data can be in table 2. It shows that the B3LYP/6-31G(d) level agrees more closely to the bond lengths in two out of the three cases. This observation, in conjunction with the dihedral angle measurement, indicates that B3LYP/6-31G(d) is slightly better at predicting the structure of antiperiplanar 1,5-hexadiene.
Optimisation of Gauche 1,5-Hexadiene
Intuitively, it would be expected that the gauche conformation would have a higher energy than that of the antiperiplanar. This assumption is founded on one factor that partially determines the stability of a compound, namely the steric congestion. When substituents about a bond are bulky and gauche, there is unfavourable repulsions between them; thereby, increasing the energy of that conformation. An analogy can be drawn to a similar molecule, butane for example, where it is known that the antiperiplanar conformation is more stable.[10]
Initially, upon optimisation of a gauche 1,5-hexadiene conformation, at the HF/3-21G level, gauche4 was obtained from appendix 1. Figure 5 displays the conformation obtained, which was found to have an energy of -231.69153032 Hartrees and a symmetry of , which was expected upon comparison to appendix 1. It was noticed, and evident from the assumptions of this calculation, that the conformation obtain from optimisation is highly dependant on how 1,5-hexadiene is initially drawn. This should not come as a surprise, owing to the fact that the constructed conformation decides the initial position on the potential energy surface. Therefore, different conformational minimum can be readily obtained from altering dihedral angles and other bond angles.
| Figure 5. Initial Gauche 1,5-hexadiene HF/3-21G level optimisation. |
Figures 6 and 7 display gauche 1,5-hexadiene before and after optimisation, respectively. One notable difference between the structures is the relative orientation of the vinyl substituents. Upon optimisation, at the HF/3-21G level, it is evident that rotation about CC bonds (specifically, the vinylic and allylic carbons) had occurred; this rotation increased the internuclear distances between vinylic hydrogen atoms and appeared to stack the alkene groups.
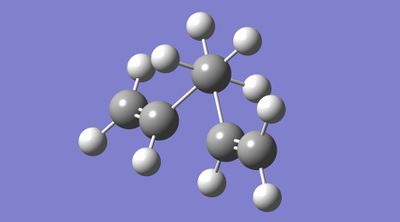 |
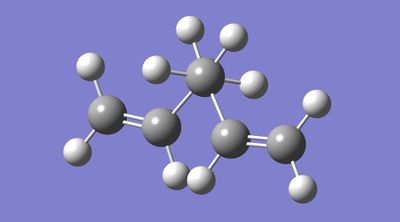 | |
| Figure 6. Gauche 1,5-hexadiene before optimisation at the HF/3-21G level. | Figure 7. Gauche 1,5-hexadiene after optimisation at the HF/3-21G level. |
Intuitively, from comparison of 1,5-hexadiene to a similar molecule, such as hexane (butane could also be taken as a simpler case), it would be expected that the antiperiplanar conformation would be lower in energy than gauche. Of the antiperiplanar structures, it would be expected that strain is less severe than the strain; both of these interactions are governed by van de Waals forces. Steric interactions are not the only interaction that determines conformational stability, stereoelectronic interactions also need to be considered. Cieplak interactions, which are a stabilising interaction from donation of a orbital into a orbital, occur about the central carbon atoms; these interactions occur for all antiperiplanar however, and gauche conformations for that matter, so this type of stereoelectronic interaction need not be considered. Interactions between bonds, which are repulsive in nature, can also be considered, but as the vinyl groups are not close, these interactions will be weak. Hence, having a trans- arrangement (this descriptor is being used loosely here to indicate that the terminal carbon atoms reside on opposite faces of the central carbon atoms) of vinyl substituents should be taken as the conformation for calculating activation energies. Out of the structures provided in appendix 1, the one with the least steric congestion is anti2; this is the conformation that intuitively would be the most stable conformation.
Gauche3 was constructed and optimised, as outlined, at the HF/3-21G level. An energy of -231.69266114 Hartrees was obtained, which is in good agreement with the value provided energy in appendix 1. Unexpectedly, it can be seen in the appendix 1 that gauche3 is the lowest energy conformation calculated at the HF/3-21G level. A point group of was observed, which was also in accordance with what was expected. Figure 8 displays the obtained conformation after optimisation.
| Figure 8. Gauche3 1,5-hexadiene optimised at HF/3-21G. |
To allow comparison of the optimised antiperiplanar 1,5-hexadiene, at the B3LYP/6-31G(d) level, the same level of optimisation was performed for the lowest energy gauche conformation. An energy of -234.61132934 Hartrees was obtained from the optimisation. Figure 9 contains the obtained conformation.
| Figure 9. Gauche3 optimised at the B3LYP/6-31G(d) level. |
As with the antiperiplanar conformation, and what was expected, the frequencies of vibration are all real. Figure 10 displays the calculated IR spectrum.
Table 4 displays the obtained energy values from performing a Frequency calculation at the B3LYP/6-31G(d) level on the lowest energy gauche 1,5-hexadiene conformation at a temperature of 298.15 K, 0.01 K and 400K. As noted with the antiperiplanar conformation, the contribution from thermal sources has essentially been reduced to zero.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 4. Summary of obtained thermochemical data at different temperatures for the B3LYP/6-31G(d) level. | |||
No visual difference were observed between the structures from the different levels. Bond lengths between carbon atoms were extracted and displayed for both levels of optimisation; table 5 displays the results. It is evident, from table 5, that there is very little difference between the bond lengths.
| Bond | HF/3-21G CC Bond lengths / nm | B3LYP/6-31G(d) CC Bond lengths / nm |
|---|---|---|
| Vinyl | 1.31630 | 1.33361 |
| Allyl | 1.50844 | 1.50439 |
| Central | 1.55326 | 1.55013 |
| Table 5. Summary of obtained CC bond distances. | ||
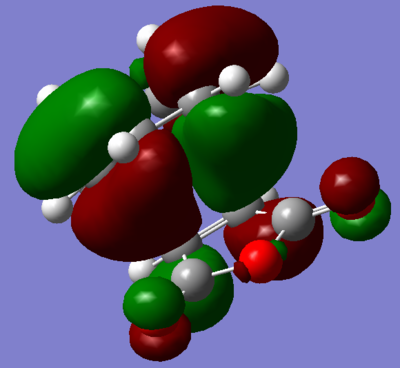
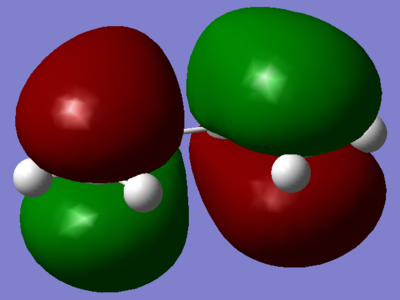
Gung et al. conducted a computational investigation of the 27 conformations of 1,5-hexadiene, 10 of which were found to be energetically distinct conformations. In which, they determined that an antiperiplanar conformation, specifically anti2 from appendix 1, to be the global minimum. However, they noted that three other structures have similar energies, and so this global minimum is not so defined. They also noted that the interaction was neglected in their calculation method.[8] On the other hand, Rocque et al. performed a similar study as Roque et al. with slightly different computational techniques and arrived at a different conclusion. Their calculations revealed that an attractive interaction between the vinyl proton and orbital results in gauche3 being the conformational global minimum.[11] If the interaction was playing a role in stabilising 1,5-hexadiene, it would be expected that evidence for it would be found in the illustrations of the MO. Figure 11 displays MO 14, which is thought to visually verify this attractive interaction.
As mentioned earlier, employing different compounds, with similar structural features, might indicate which conformation is the global minimum. Energy calculations of different conformations of n-butane has been studied extensively; Wiberg et al. reported a 0.86 kcal/mol difference in energy between gauche and antiperiplanar conformations, the latter of which being the more stable. Intuitively, a similar result was expected for 1,5-hexadiene. [10]
A review of interactions, sourced from the Cambridge Structural Database, reported by Umezawa et al., concluded that these interactions play an appreciable role in determining the conformational minimum of 1,5-hexdiene. Their study revealed that large numbers of organic compounds exhibit surprisingly short distances between the vinylic proton and orbitals.[9] On the contrary, an electron diffraction study of gaseous 1,5-butadiene concluded antiperiplanar conformations being more stable.[12]
Overall, it is not clear which conformation of 1,5-hexadiene, be it anti2 or gauche3, is the global minimum. However, owing to the small energy differences between them, it is not terribly important which one is the global minimum, as long as calculations are taken from one of these structures. Despite this fact, anti2 shall be taken as the lowest energy conformation for further calculations, as it was determined to have the lowest energy from optimisations at the B3LYP/6-31G(d) level, which is considered to be more accurate than HF/3-21G.
Nf710 (talk) 17:00, 25 February 2016 (UTC) Fantastic use of references to back up your arguement. It is extremly balanace and well argued. and you have put forward and excellent reason why to use anti 2. In your use of the MOs to show the overlap. I would have used a slightly less sparse value for the orbitals
Transition States of 1,5-Hexadiene
It is known that the Cope rearrangement proceeds by a cyclic transition state. Therefore, basing guess transition state structures on cyclohexane seems to be a reasonable approach. Two conformations of cyclohexane have been chosen as guess transition structures, those being: a chair conformation, which is the lowest energy conformation; and a boat conformation, which is a energy maxima species. Hammond's postulate could be applied to try and uncover information about the transition structure. As the reactant and product are identical, Hammond's postulate predicts that the transition state should resemble the reactant and product; it does not matter in this case.[4] Figure 12 displays the Cope rearrangement with a generalised transition structure connecting the two 1,5-headienes.
Wiest et al. reported that chair and boat transition state conformations in the Cope rearrangement were of importance. Figures 13 and 14 display these, respectively.[13]
| Figure 13. Guess chair transition state structure. | Figure 14. Guess boat transition state structure. |
Gung et al. stated that the conformation seen in figure 15 was important in the Cope rearrangement.[8] It is evident that overlap of terminal carbon atoms p-orbitals is possible in this conformation. If this conformation is inspected further, it becomes evident that there is resemblance to the chair conformation of cyclohexane. However, they did not report that the conformation seen in figure 16 was of any importance. By analogy, it is clear that this conformation resembles the boat transition structure most closely. These conformations can be seen to be similar to gauche2 and gauche6 in appendix 1, respectively.
 |
 | |
| Figure 15. Conformation that is expected to be related to the chair. | Figure 16. Conformation that is expected to be related to the boat. |
In this section, the same calculation levels were utilised, but the type of calculation performed was slightly different. Instead of optimising to a minimum energy, the optimisation was to a maximum in energy. Two methods were used to achieve the maximum on the potential energy surface to be found, namely: TS(Berny) and QST2. Once the IRC had been obtained, optimisation of the product was performed for the minimum energy.
Chair Transition State
One of the guessed transition states for the Cope rearrangement involves a chair like transition state; the structure of which can be seen in figure 13. This section of the report describes the results of the outlined calculations.
An allyl fragment was constructed, as seen in figure 17 below, and optimised to a minimum at the HF/3-21G level.
| Figure 17. Allyl fragment optimised to a minimum at HF/3-21G. |
Upon optimisation of the allyl unit, the energy was -115.82304010 Hartrees. As expected, a point group of was obtained.
As instructed, two of the optimised allyl units were arranged in a chair like conformation and interatomic distances between terminal carbon atoms were set to 2.2 Angstroms with the aid from symmetrize. Figure 18 and 19 display the initial guess chair transition state and the output from a transition state (TS(Berny)) optimisation at the HF/3-21G level, respectively. An energy of -231.61932234 Hartrees was obtained for this optimisation, which was found to be in good agreement with the value provided in the appendix. A point group was found for the transition state.
Bond lengths for the those that form/break were found to have distances of 2.01997 Angstroms after optimisation. This interatomic distance is significantly larger than the putative CC bond distance, which has a value of 1.54 nm. As this is a transition state structure, a lengthening of normal bond lengths is expected.
| Figure 18. Chair conformation before optimisation at the HF/3-21GTS(Berny) level. | Figure 19. Chair conformation after optimisation at the HF/3-21GTS(Berny) level. |
A single imaginary frequency, corresponding to the Cope rearrangement, was observed at -818.04 wavenumbers. An imaginary frequency is observed for transition states because of the relationship between the force constant and the second derivative of the potential energy surface. Equation 3 describes the relationship between the force constant and potential energy; where , and are the force constant, displacement and potential energy, respectively. Transition states are defined as the maximum on a potential energy surface; if the second derivative of which is taken, a negative value is obtained.[14]
(3)
The frequency of vibration is related to the force constant by equation 4; where and are the frequency of vibration and effective mass, respectively. If the square root of a negative number is taken, the resulting value is imaginary. Hence why the vibration is referred to as imaginary.[14]
(4)
Figure 20 displays the Cope rearrangement vibration, which appears to occur in a concerted manner.[15] It is evident that one pair of the terminal carbon atoms approaches each other, while the other lengthens. A lengthening of the bond between the vinylic and allylic carbon atoms is seen, while the vinylic bond distance decreases; these changes in bond length correspond to the formation of a single and double bond, respectively.
Table 6 displays the energy values, calculated with the HF/3-21G TS(Berny) basis set under standard conditions, for the chair transition state. These are all in good agreement with the provided values in the results table of appendix 2.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 6. Summary of obtained thermochemical data for the HF/3-21G TS(Berny) level. | |||
Optimisation of the HF/3-21G TS(Berny) structure was then performed with frozen coordinates for terminal carbons. Frozen coordinates fixes the interatomic distances between specified atoms, which allows optimisation of the remaining transition state structure to occur without dealing with the crucial bonds. The frozen bonds are the bond forming and breaking ones, which will be highly influential in determining the overall structure and energy. An energy of -213.61518445 Hartrees and point group was obtained for the frozen coordinate optimisation. The obtained structure for which can be seen in figure 21, below. It can be seen, in the figure below, that the interatomic distances between terminal carbons has been fixed at 2.2 Angstroms.
| Figure 21. Frozen coordinate optimisation of chair transition state structure. |
From the frozen coordinate optimisation, a derivative optimisation was then performed to determined the optimal geometry of terminal carbons. Optimisation yielded a point group of , an energy of -231.61932233 Hartrees, and structure that can be seen in figure 22.
| Figure 22. Derivative optimisation of chair transition state structure. |
For the derivative calculation, the bond distances were 2.02074 Angstroms, which if compared to figure 19, can be seen to be slightly longer. However, the difference is negligible.
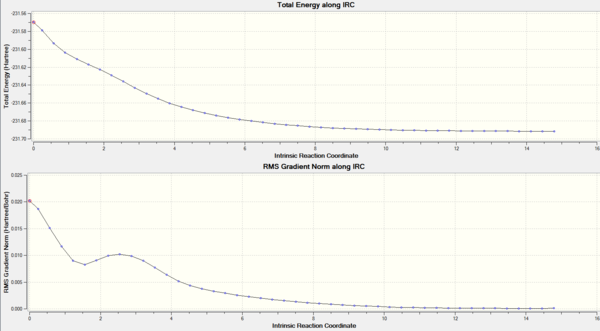
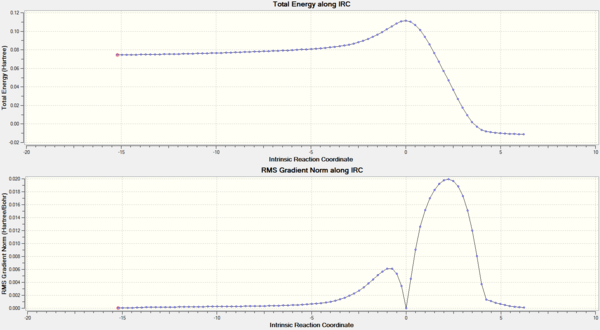
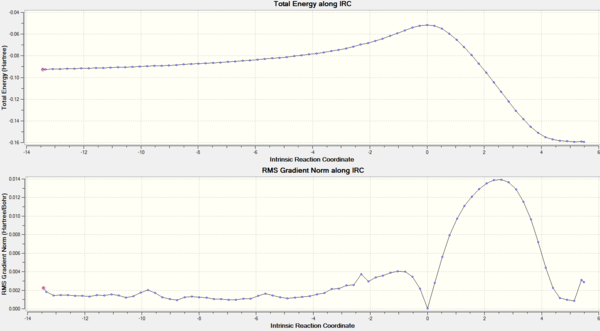
An intrinsic reaction coordinate (IRC) calculation, from the HF/3-21G TS(Berny) level optimised transition structure, was then calculated. This type of calculation samples derivatives of the surrounding potential energy surface, finds the maximum downhill path, takes a step in that direction and iterates until a minimum is reached. The resulting position on the potential energy surface should be the most stable compound from the initial transition state structure. Figure 23 displays the IRC, in which, it can be seen that the energy decreases from a maximum, as expected. Initially, there was a large reduction in the energy, which corresponded to the IRC stepping away from the transition state towards a stable molecule. Nearer the end of the IRC, only small changes in energy occur because of the calculation attempting to find the lowest possible minimum. As the reaction coordinate for the Cope rearrangement is symmetrical, there was no need to calculate the forwards and backwards reaction coordinates from the transition state structure. In total, 46 steps were required for the calculation to converge.
An animation of the IRC was produced and displayed in figure 24. It clearly shows 1,5-hexadiene starting from the chair transition structure, altering bond angles and distances until the gauche2 conformation was obtained. The cope rearrangement was expected to have a concerted mechanism, where one bond breaks, two bonds shift position and another bond forms. From the transition state structure, which is a highly symmetric species, it can be seen that a bond forms at the expense of another. Inspection of the IRC reveals that there are two maximums in the derivative of the potential energy surface. The first of which occurs at the transition state and the second some time after. Figure 24 was utilised to correlate these maximum to structural changes that occurred. It was found that the second maximum in the gradient of the potential energy surface corresponded to bond formation. A maximum in the gradient of the potential energy surface was observed because of the nature of the transition state.
Some altered IRC calculations were suggested in the instructions to aid the calculations to converge. The first of which entailed altering the number of times the force constants was calculated. Instead of calculating the force constants every third step, calculation of the force constant at each step was performed. An energy of -231.691614566 Hartrees was obtained for the final structure. This slight difference in energy can be attributed to the numerical nature of the calculations. Another alteration was to increasing the number of steps perfumed. As the calculation converged in a fewer number of steps than specified, increasing the number of steps would be redundant. Hence, this was not performed.
Optimisation of HF/3-21G chair transition structure at the B3LYP/6-31G(d) yielded and energy of -234.55697014 Hartrees. Table 7 displays the obtained thermochemical data of the named optimisation; these are in good agreement with those displayed in the summary of energies of appendix 2.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 7. Summary of obtained thermochemical data for the B3LYP/6-31G(d) level. | |||
The imaginary vibration at this level was found to have a value of -565.46 wavenumbers. Clearly, there is a stark difference between the imaginary vibrations at the two different levels. This comes as no surprise as the different levels have considerable differences in their assumptions. Form the differences, it can be inferred that the gradients of the potential energy surfaces are different at the transition sate structure.
A comparison of optimised chair transition structure, from the final frame of the IRC, and known conformations of 1,5-hexadiene was undertaken. It is evident that obtained conformation bears some resemblance to gauche2, in appendix 1. However, as the transition state has higher symmetry compared to gauche2 the resemblance is fairly loose. To elucidate the conformation that yields the transition structure, a comparison of the HF/3-21G optimised final frame (the 46th output, which is the one that the calculation converged to) from the IRC was made with the conformations displayed in appendix 1. Figure 25 displays the obtained structure. It was evident that the conformation resembled that of gauche2 and had the same energy. These structures however, were not identical, the obtained had hydrogen atoms on the opposite sides of the vinyl groups. The conformations are energetically identical, so they are referred to as an enantiomeric pair.
| Figure 25. Frame 46 from IRC optimised at HF/3-21G. |
A more accurate description of the Cope rearrangement mechanism can be deduced in light of this information. Initially, 1,5-hexadiene residse in one of the more stable conformations, namely gauche3 or anti2. Rotation about the allylic bond affords gauche2 from gauch3; once the molecule is in this conformation, the transition state may be reached and the reaction can proceed.
Boat Transition Structure
Another plausible transition state, as mentioned earlier, was the boat. An investigation into thermochemical data, animation of the rearrangement and calculation of IRC was conducted, using several different methods, and outlined in this section.
An antiperiplanar starting conformation, namely anti2, was chosen as the starting and end point for the QST2 optimisation of the transition state. The previously HF/3-21G optimised anti2 was used for these calculations. It was noted in the script that the calculation should fail. Upon performing the calculation, there was not an error message as one would think. However, the error was not a failure in the calculation, but a failure of the method to locate the correct minimum on the potential energy surface. An energy of -231.61932229 Hartrees was yielded, which, if compared to the chair transition structure in appendix 2, had a good agreement. Figure 26 displays the output from this failed TS optimisation, which can clearly be seen not to resemble a boat, but a chair.
| Figure 26. Failed calculation for boat transition state. |
QST2 takes the starting material and product of a reaction and attempts to find the maximum in the potential energy surface; in a sense, it is essentially the opposite of the IRC, in terms of what it is trying to find. As the chair transition state was found, it indicates that the method failed to identify CC bond rotation as a maximum change in energy as a function of internuclear coordinates. Hence, alterations should be implemented to aid the calculation.
To obtain the correct conformation from the calculation, adjustments were implemented, as suggested, to locate a more suitable initial point on the potential energy surface. Optimisation at the HF/3-21G TS(Berny) level yielded an energy of -231.602280200 Hartrees, which agrees with the provided value in appendix 2. The obtained structure has been displayed in figure 27.
| Figure 27. Successful calculation for boat transition state at the HF/3-21G QTS2 level. |
An interatomic distance of 2.14 Angstroms was observed between terminal carbon atoms on the optimised boat transition structure. If these values are compared to those of the chair transition structure, it is evident that they are slightly longer; suggesting that the boat transition state is less stable than the chair.
The single imaginary vibration in the IR spectrum was located at -839.94 wavenumbers, which is more negative than the chair transition structure. Indicating that there is a larger force constants, and therefore, a larger curvature in the potential energy surface. This deduction supports the conclusion previously drawn.
Values for the thermochemical data is displayed in table 8 for the boat transition structure optimised at the HF/3-21G TS(Berny) level. These are all in good agreement with the provided values in the results table of appendix 2.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 8. Summary of obtained thermochemical data for the HF/3-21G TS(Berny) level. | |||
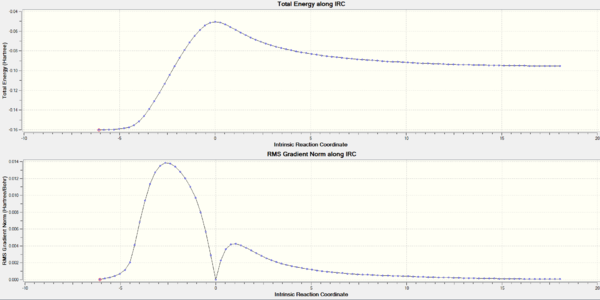
An IRC, seen in figure 28, was calculated and shown to complete in 45 iterations. The final conformation had an energy of -231.68298131 Hartrees. Comparison of figure 28 and 24 reveal some differences. To start with, there is only one maximum in the gradient of the potential energy surface, while the latter contained two. Both of these maximums were found to correspond to bond formation, from comparisons to the animated structures. In addition, the gradient of the potential energy surface was initially zero for the boat conformation, while the chair had a maximum in the gradient of the potential energy surface. Indicating that the boat transition state has a larger area of internuclear coordinates that are at a maximum.
Figure 29 is the animation produced from combing frames from the IRC. As with the chair transition state, the formation of a bond can be seen to occur at the expense of another bond. [15]
Frame 45 from the IRC was copied and pasted into a new window. Optimisation at the HF/3-21G level yielded an energy of -231.68302549 Hartrees and structure seen in figure 30. Comparing the obtained energy to those found in appendix 1 found no matches. The reason being, is that this conformation had eclipsed substituents, while all of the others have staggered. Conformations in appendix 1 with the closest energy are gauche5 and gauche6; these appear to bear some resemblance to the boat transition structure, in the sense that they have the vinylic hydrogens pointing in the same direction.
| Figure 30. Optimised final frame from IRC at HF/3-21G level. |
As the calculation converged in less than the specified number of steps, an additional calculation was not performed with extra steps, owing to the fact that it would stop once it has converged. A calculation was performed which computed the force constants at each step; no signifincat difference between the obtained energies was found.
Optimisation of boat transition state yielded and energy of -234.54309306 Hartrees at the B3LYP/6-31G(d) level. Table 9 summarises the data, which was found to be in good agreement with the provided values in the results table of appendix 2.
A lower wavenumber of the imaginary vibration was in accordance with what was previously found for the chair transition state. At the B3LYP/6-31G(d) level, the Cope rearrangement was found at -530.30 wavenumbers.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 9. Summary of obtained thermochemical data for the B3LYP/6-31G(d) level. | |||
If the boat transition state is compared to the known conformation of 1,5-hexadiene, it is evident that it resembles none of the stable ones. As the vinyl groups are eclipsed, the conformation that it would resemble would be a maxima. If bond rotation occurred however, the structure would probably resemble a gauche conformation, owing to the fact that minimal bond rotation would need to occur. Figure 30 displays the optimised final frame of the IRC; it is clear, from the figure, that the vinyl groups are still eclipsed.[8]
Nf710 (talk) 17:16, 25 February 2016 (UTC) You could have optimised down the final product
Nf710 (talk) 17:17, 25 February 2016 (UTC) But excellent work in determining the boat IRC and a very good arguement for the two structures
Activation Energy
The summarised thermochemical data for calculations at the HF/3-21G level could be found in the previous sections. To calculate the activation energy of the Cope rearrangement, the difference in energy between the lowest energy conformation (anti2) and the optimised transition state structures. Table 10 displays the obtained results in more conventional units.
| Structure | Energy of Activation / kcal/mol (298.15 K) | Energy of Activation / kcal/mol (0.01 K) | Energy of Activation / kcal/mol (400 K) |
|---|---|---|---|
| Chair | 44.69 | 45.71 | 44.48 |
| Boat | 54.76 | 55.60 | 54.61 |
| Table 10. Summary of calculated activation energies at the HF/3-21G level from anti2. | |||
Exactly the same procedure was repeated for the calculations performed at the B3LYP/6-31G(d) level; table 11 displays the activation energies obtained.
| Structure | Energy of Activation / kcal/mol (298.15 K) | Energy of Activation / kcal/mol (0.01 K) | Energy of Activation / kcal/mol (400 K) |
|---|---|---|---|
| Chair | 33.16 | 34.06 | 32.74 |
| Boat | 41.32 | 41.96 | 41.01 |
| Table 11. Summary of calculated activation energies at the B3LYP/6-31G(d) level from anti2. | |||
Literature sources reported experimental activation energies of the chair and boat transition state structures, at 0K, at 33.5 +/- 0.5 kcal/mol and 44.7 +/- 2 kcal/mol, respectively.[13] Comparing the obtained activation energies to literature demonstrates that the B3LYP/6-31G(d) level is more accurate.
Cope Rearrangement Conclusion
To conclude, it was found that the anti2 conformation is probably the global minimum for 1,5-hexadiene. Numerous interactions need to be simultaneously considered when determining which conformation should be the global minimum, which makes it extremely difficult to accurately predict. Furthermore, conflicting computational and experimental results for the global minimum of 1,5-hexadiene furthers the confusion.
It was found that the chair transition state structure was the more stable of the two; this conclusion was drawn from the fact that it exhibited a lower energy, smaller CC internuclear distance between fragments and smaller negative wavenumber for the imaginary vibration. Furthermore, a smaller activation energy was obtained for the chair conformation, which indicates that the transition state is more favourable than the boat.
Nf710 (talk) 17:25, 25 February 2016 (UTC) You have the correct energies well done. you should have come to the conclusion that minimal basis sets are still good at determining geoms but not very good at energies. This report is very very good. you have gone the extra mile and compared both the boat for and chair for ircs. You have found extra literature and used in very good weighted arguments. the only thing that you could have improved on is the understanding of the various computational processes.
Diels-Alder
The following section outlines the optimisation of starting materials and guess transition structures, calculation of relevant thermochemical and IRC, and analysis of the obtained results for two Diels-Alder cycloadditions. Essentially the same procedure was employed for this section as was outlined for the previous for the Cope rearrangement.
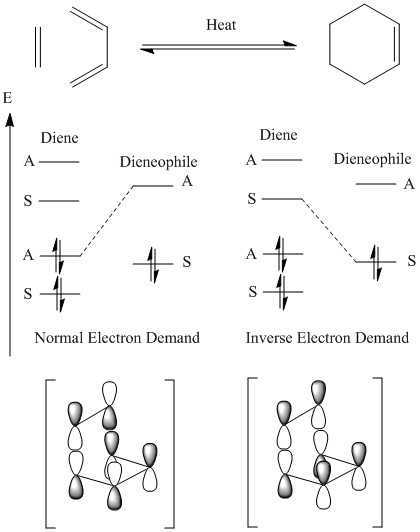
As mentioned in the previous section, cycloadditions are another class of pericyclic reaction, the most notable of which is the Diels-Alder, which is defined as a [4+2]-cycloaddition. In these reactions, two unsaturated units (these unsaturated components can either be in the same molecule or different ones) cyclise to afford two new bonds with the loss of one bond.[1][16] According to the Woodward-Hoffman rules, there must be a conservation of symmetry and favourable energetics for the reaction to proceed.[3] Furthermore, as Diels-Alder cycloadditions are a type of pericyclic reaction, there is a concerted mechanism and cyclic transition state with suprafacial/suprafacial (note: antarafacial/antarafacial interactions are possible, but do not tend to be seen for Diels-Alder cycloadditions) interactions between components.
Diels-Alder reactants are classified into two parts: diene and dienophile.[1] Interaction of these components can occur in two distinct ways, which depend on the relative orientation of the components (exo and endo, described in proceeding paragraph). For one of these transition states, the relative energy of the MO's, which is determined by the substituents on the diene and dienophile, dictates what type of electron demand.[1] If the HOMO on the diene interacts with the LUMO on the dienophile, then the cycloaddition is referred to as a normal electron demand; whereas, for the opposite interaction the reaction is classified as inverse electron demand. Adding electron donating groups to the diene raises the energy of the MO's and electron withdrawing groups to the dienophile lowers the energy of the MO's, which results in a more favourable normal electron demand orbital interaction.[17]
Hammond's postulate can be employed to guess plausible transition state structures for Diels-Alder reactions. As the product tends to be more thermodynamically stable, owing to the larger number of bonds, the transition state structure should resemble the products.[4] For a [4+2]-cycloaddition, the transition structure resembles a cyclohexene ring. However, when the dienophile has an extended system, secondary orbital overlap becomes possible. Secondary orbital overlap is a stabilising interaction between orbitals of each component that arises from a specific geometry of the transition state structure. When this occurs, the product is referred to as endo, and exo when it does not. The former is the kinetic product, while the latter the thermodynamic.[1] These differences arise in the stability of the transition state and product.
Prototype Diels-Alder
A prototypical Diels-Alder reaction, between ethene and cis-butadiene, was attempted first; the reaction scheme for which can be seen in figure 31. Consideration of the specific geometry of the transition state is relatively easy for this reaction because of the high degree of symmetry and basic nature of reactants. Figure 31 also contains a qualitative energy diagram of the relevant orbitals involved in the cycloaddition. As outlined in the previous section, there are two types of reaction that can occur: inverse electron demand and normal electron demand. The former of which, as seen in figure 31, involves donation from ethene's HOMO into cis-butadiene's LUMO; whereas, the latter donates electron density from the HOMO of cis-butadiene to the LUMO of ethene. Normal electron demand is the orbital interaction that this reaction proceeds by. It can also be seen that the symmetry of the interaction orbitals are the same for both of these reactions, which is a requirement from the Woodward-Hoffman rules. An illustration of these two interactions has been drawn underneath the respective energy diagram in figure 31.
Ethene and cis-butadiene were constructed and optimised at the semi-empirical (SE) AM1 level. The former was found to have an energy of 0.02619027 Hartrees, while the latter 0.04879718 Hartrees. Optimised structures for which can be found in figures 32 and 33, respectively.
| Figure 32. Optimised ethene at the SE AM1 level. | Figure 33. Optimised cis-butadiene at the SE AM1 level. |
Thermochemical data was obtained for both of starting materials under standard temperature (298.15 K), low temperature (0.01 K) and high temperature (400 K). Table 12 summarises the obtained data for ethene, while table 13 for cis-butadiene.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 12. Summary of obtained thermochemical data for ethene at the SE AM1 level. | |||
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 13. Summary of obtained thermochemical data for cis-butadiene at the SE AM1 level. | |||
As outlined in the prelude, Diels-Alder cycloadditions can only occur if a HOMO-LUMO interaction occurs with a favourable energy and conservation of symmetry. Furthermore, at the start of the section, figure 31 was displayed, which contained the expected interaction for the Diels-Alder cycloaddition. To confirm the expected interactions, calculations of the MO's for ethene and cis-butadiene were performed. Figures 34 through 37 display the calculated HOMO and LUMO for ethene and cis-butadiene, respectively. These calculated MO's are in good agreement with those expected.
 |
 | |
| Figure 34. HOMO of ethene. | Figure 35. LUMO of ethene. | |
 |
 | |
| Figure 36. HOMO of cis-butadiene. | Figure 37. LUMO of cis-butadiene. |
(Missed out the images for ethene in the table above Tam10 (talk) 15:12, 23 February 2016 (UTC))
If figures 34 and 35 are inspected, it can be seen that the HOMO of ethene was symmetric (S) with respect to the plane, while the the LUMO was anti-symmetric (AS) with respect to the plane. Whereas, cis-butadiene had the opposite symmetry, with regard to reflection in the provided plane, for the same respective orbitals. These orbital interactions were in good agreement with those reported in literature.[18]
As described in the previous section, a guess transition state structure can be obtained from employing Hammond's postulate. Cyclohexene is the product of this prototypical Diels-Alder reaction, which is known to be more thermodynamically stable than the starting materials (can be seen from the optimised starting materials and product). A guess transition structure was based on bicyclo(2.2.2)octa-2,5-diene, instead of cyclohexene, as the transition state is known to have a large envelope character. Optimisation of this structure, at the SE AM1 level, was performed; figure 38 displays the obtained structure. The SE AM1 optimised bicyclo[2.2.2]oct-2-ene was transferred to a new window, where the alkyl and vinyl groups were removed, the former of which was replaced by a pair of hydrogen atoms. Optimised ethene was transferred to the same window and position appropriately. It was noticed in the previous section that placing the reactants at slightly longer bond distances yielded good TS optimisations. As optimised TS structures in the previous section had interaction distances at roughly 2.1 Angstroms, the interatomic distances between ethene and terminal carbon atoms in the diene component were set to 2.1 Angstroms. Figure 39 displays the structure obtained from the described calculation.
| Figure 38. Optimised bicyclo(2.2.2)octa-2,5-diene at the SE AM1 level. | Figure 39. Optimised guess transition state structure for prototypical Diels-Alder cycloaddition. |
An energy of 0.11165465 Hartrees was obtained for a SE AM1 TS(Berny) level optimisation. An imaginary vibration was observed at -956.37 wavenumbers, which corresponded to the vibration seen in figure 40; this is clearly the vibration associated with the expected Diels-Alder cycloaddition. Evidently, from this animation, the bond forming/breaking occurs in a concerted manner, which was expected from the definition of a pericyclic reaction.[15]
The lowest positive frequency of vibration occurred at 147.20 wavenumbers. This vibration, which can be seen in figure 41, involves rotation of ethene with respect to cis-butadiene.
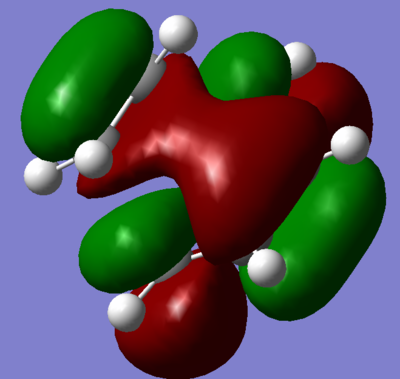
Figure 42 and 43 display the HOMO and LUMO for the SE AM1 optimised transition structure, respectively. These MO's should resemble the normal electron demand and inverse electron demand cycloadditions, respectively.
 |
 | |
| Figure 42. HOMO of the transition state for the prototypical Diels-Alder. | Figure 43. LUMO of the transition state for the prototypical Diels-Alder. |
Inspection of the HOMO and LUMO, with respect to reflection, in the plane described by the script, it is evident that the same symmetry is observed for the transition state as the starting materials. This was expected, as one of the selection rules of the Woodward-Hoffman rules is that must be no change in orbital symmetry.
Figure 42 displays the HOMO for the transition state, which was anti-symmetric with respect to reflection in the provided plane. If the HOMO of the transition state is compared to figure 34 and 37, it can be seen that overlapping the orbitals in these figures produces the transition state. As these orbitals are of the same symmetry, they were expected to overlap; this is the reason why the two compounds react in a Diels-Alder fashion.
Table 14 displays the measured interatomic distances for transition state structure; T and C refer to terminal an central carbon bonds, respectively. If a comparison of the partial bond is made to those obtained for the Cope rearrangement in the previous section, it can be seen that they are fairly similar. Comparison of the CC bond lengths in the transition state to the reagents and product should reveal the extent to which bond formation has occurred. The interatomic distance of CC in ethene was found to be 1.31510. Clearly, the CC bond in the ethene unit of the transition state is longer, which suggests that donation of electron density into the has occurred to some extent. It can be seen that essentially all of the CC bonds, apart from the partial (between terminal atoms of each unit), are very similar. Hence, validating the observation of a concerted mechanism.
| Bond | CC Bond lengths / nm |
|---|---|
| Partial | 2.11916 |
| Ethene | 1.38291 |
| Vinyl - T | 1.38187 |
| Vinyl - C | 1.39748 |
| Table 14. Summarised interatomic distances between carbon atoms in the transition state. | |
(Units should be Å here Tam10 (talk) 15:12, 23 February 2016 (UTC))
An IRC was then calculated for this prototypical Diels-Alder cycloaddition. As the reaction coordinate is not symmetrical, instead of just calculating the forward path, as it was for the Cope rearrangement, both directions had to be computed. Figure 44 displays the obtained intrinsic reaction coordinate. It is evident, from this figure, that the reaction coordinate is not symmetrical, which was expected.
An animation of the obtained IRC was produced and displayed in figure 45. It can be seen that ethene approaches from a distance and at an angle that is not favourable for a Diels-Alder cycloaddition. When ethene is in the vicinity of cis-butadiene, it rotates, so to allow the most favourable orbital overlap, and starts interacting with hydrogen atoms before the cycloaddition occurs. It is evident, from the fact that the two bonds are made simultaneously, that the reaction proceeds in a concerted manner. This observation can be verified by the vibration associated to the transition sate, which can be seen in figure 40. This result comes as no surprise, owing to the fact that a concerted mechanism is one of the defining features of a pericyclic reaction.
The final frame from the IRC was optimised at the SE AM1 level and found to have an energy of -231.720374017 Hartrees. Thermochemical data for The HF/3-21G level was calculated at three different temperatures; table 15 summarises the obtained values. No negative frequencies of vibration were observed.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 15. Summary of obtained thermochemical data for cis-butadiene at the SE AM1 level. | |||
From tables 12, 13 and 15, the activation energy at different temperatures can be calculated. Temperates of 298.15 K, 0.01 K and 400 K where investigated, which yielded activation energies of 48.38 kcal/mol, 48.30 kcal/mol and 48.63 kcal/mol, respectively. Literature reports the experimentally measured activation energy at 27 +/- 2 kcal/mol[19] [20]. It is evident that the obtained is not in good agreement with literature.
As cis-butadiene has been used as the starting conformation for the Diels-Alder reaction, it was taken for the activation energy calculation. This is not strictly correct, as activation energy tends to be calculated from the lowest energy conformation, which would be trans-butadiene, and so it should be noted that the activation energy calculated here is slightly lower than expected.
Diels-Alder Regioselectivity
This section aimed to describe a Diels-Alder cycloaddition between two, more complicated molecules that should exhibit interesting stabilising interactions. In the previous section, a prototypical Diels-Alder reaction was investigated, where a fairly simple orbital model was successfully employed to describe the reaction. However, with the introduction of electron withdrawing groups and the possibility of second order orbital overlap, further considerations about the transition state structure need to be analysed.
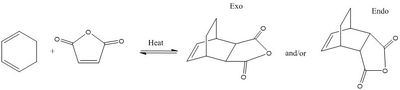
Below, figure 46, displays the Diels-Alder cycloaddition between cyclohexa-1,3-diene and maleic anhydride. In which, two products, related by regioselectivity, have been shown to form: endo and exo.
 |
|---|
| Figure 46. Reaction scheme for Diels-Alder cycloaddition between cyclohexa-1,3-diene and maleic anhydride. |
Both of the following sections require the same starting molecules, which are then arrange in different ways to probe the endo and exo transition state structures. Hence, the optimisation of cyclohexa-1,3-diene and malice anhydride shall be discussed separately so that they can be used in the proceeding two sections. In a similar manner to the prevision section, the diene used in the transition state structure was not actually cyclohexa-1,3-diene, but a bicyclic analog. Deleting only the vinyl groups, from bicyclo(2.2.2)octa-2,5-diene, yielded the required structure for these calculations. For the relevant figures and energies, the previous section should be consulted. Optimisation of maleic anhydride, at the SE AM1 level, can be seen in figure 47; an energy of -0.12182410 Hartrees was obtained. An optimisation at the HF/3-21G level, followed by the B3LYP/6-31G(d) yielded an energy of -379.289544571 Hartrees. Clearly, the energy obtained from SE AM1 and B3LYP/6-31G(d) calculations was significantly. To highlight this point further, an optimisation of cyclohexa-1,3-diene was performed at the B3LYP/6-31G(d) level. An energy of -233.418936316 Hartrees was obtained; again, this is significantly lower.
| Figure 47. Optimised maleic anhydride at the SE AM1 level. |
Table 16 displays the obtained thermochemical data for maleic anhydride at the SE AM1 level.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 16. Summary of obtained thermochemical data for maleic anhydride at the SE AM1 level. | |||
Optimisation of cyclohexa-1,3-diene, at the SE AM1 level, was performed for calculation of the activation energy; figure 46 displays the obtained results, which had an energy of 0.02771128 Hartrees.
| Figure 48. Cyclohexa-1,3-diene optimised at the SE AM1 level. |
Thermochemical data for cyclohexa-1,3-diene is displayed in table 17.
| Parameter | Energy / Hartrees (298.15 K) |
|---|---|
| Sum of electronic and zero-point energy | |
| Sum of electronic and thermal energies | |
| Sum of electronic and thermal enthalpies | |
| Sum of electronic and thermal free energies | |
| Table 17. Summary of obtained thermochemical data for cyclohexa-1,3-diene at the SE AM1 level. | |
MO's for maleic anhydride and cyclohexa-1,3-diene were computed to see if the relevant orbitals could be identified. It is expected that, for both of the reactions, normal electron demand should occur. Therefore, the HOMO of cyclohexa-1,3-diene should interact with the LUMO of maleic anhydride. Figures 49 and 50 display these orbitals, respectively.
From these figures, it can clearly be seen that they posses the same symmetry. This observation is in accordance with allowed processes according to the Woodward-Hoffmann rules.
Endo Transition State Structure
This section considers the formation of the endo product from cyclohexa-1,3-diene and malice anhydride. As described in the prelude, this product should form with secondary orbital overlap aiding the transition state. Despite these stabilising interactions in the transition state, there is destabilising repulsions in the product. Figure 51 displays the reaction scheme, qualitative energy level diagram and expected orbital overlap for the endo transition state structure.
 |
|---|
| Figure 51. Reaction scheme, qualitative energy level diagram and expected orbital overlap for the endo transition state structure. |
Optimised maleic anhydride and bicyclo[2.2.2]oct-2-ene were transferred to a new window, tweaked and arranged in the same orientation as that seen in figure 51, seen above. Optimisation of this structure, at the Se AM1 TS(Berny) level, was then conducted; the obtained structure can be seen in figure 52. An energy of -0.05150477 Hartrees was obtained.
| Figure 52. Optimised endo transition state structure at the SE AM1 level. |
As expected, one imaginary vibration was observed, which corresponds to the endo transition state structure, at -806.01 wavenumbers. Figure 53 displays the animated vibration, which was found to be concerted in nature. [15]
It was expected that the transition state proceeded by normal electron demand. Figure 51, at the start of this section, displayed the expected orbital interaction for this type of electron demand. Figures 49 and 50, seen in the prelude, show the orbitals that are expected to interact. If these orbitals are mentally overlapped, it can be seen to agree with the HOMO of the transition state, seen in figure 54. From inspection, it was found that the LUMO of the transition state is composed of the same orbitals as the HOMO, but with the phase inverted. Hence, this is an unfavourable interaction.
To find evidence for the expected secondary orbital overlap, MO's of the HOMO-LUMO region were computed for the optimised transition state structure; figures 54 through 57 display the MO's. Clearly, secondary orbital overlap can be seen in figures 56 and 57. The LUMO +2, seen in figure 57, is composed of the LUMO +1 from maleic anhydride (figure 58) and cyclohexa-1,3-diene (figure 59). Whereas, the HOMO from maleic anhydride (figure 60) was the closest match and LUMO from cyclohexa-1,3-diene (figure 61) to produce the secondary orbital overlap seen in the LUMO +1 of the transition state.
Figure 60 displays the HOMO for maleic anhydride. Inspection of the nodal properties reveal that there is a nodal plane across the plane that maleic anhydride lies. Furthermore, it can be seen that nodal planes are observed between the three oxygen atoms p-orbitals; all of which have a node with the vinyl unit as well. These nodal planes allow maleic anhydride reaction with cyclohexa-1,3-diene and provide the correct symmetry to allow secondary orbital overlap.
Bond lengths and notable interatomic distances were acquired from the output of the optimised transition state structure; table 18 summarises the obtained data. In the table, A and B refer to cyclohexene and maleic anhydride, respectively. Allyl and Pre-Allyl bonds refer to the bonds that are allyl in the transition state and the bonds that were allyl in the starting material, respectively. As with the prototypical Diels-Alder reaction, it can be seen that the partial bond is extended and the remaining carbon atoms have an intermediate distance between single and double.
| Bond | CC Bond lengths / nm |
|---|---|
| Partial | 2.16252 |
| Alkene - A | 1.39725 |
| Allyl - A | 1.39306 |
| Pre-Allyl - A | 1.49055 |
| Alkyl - A | 1.52293 |
| Alkene - B | 1.40845 |
| (CO)O(CO) - B | 2.27924 |
| Table 18. Summary of obtained CC bond distances for the endo transition state structure. | |
The obtained thermochemical data for the endo transition state structure has been summarised in table 19.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 19. Summary of obtained thermochemical data for the endo transition state at the SE AM1 level. | |||
An IRC was computed for the endo transition state and displayed in figure 62. As expected, the reaction coordinate is not symmetrical.
Figure 63 displays the produced animation from the IRC.
The final frame of the IRC, which corresponds to the adduct from the Diels-Alder, was optimised at the SE AM1 level. Figure 64 displays the optimised structure, which was found to have an energy of -0.16017023 Hartrees. Thermochemical data was obtained and displayed in table 20.
| Figure 64. Optimised final frame from IRC at the SE AM1 level. |
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 20. Summary of obtained thermochemical data for product from the endo transition state at the SE AM1 level. | |||
The activation energy for the endo transition state was found to have a value of 27.70 kcal/mol at 298.15 K. This was found to be in poor agreement with literature, which reported a value of 11.4 kcal/mol.[21]
Exo Transition State Structure
In the exo transition state, it is expected that no secondary orbital overlap is observed, but the product exhibits less steric congestion from van de Walls interactions. This transition state is often referred to as the thermodynamic one, owing to the fact that the thermodynamic product is formed; while the endo transition state is known as the kinetic transition state. Figure 65 displays the reaction scheme, qualitative energy diagram for the relevant orbitals, and expected orbital overlap.
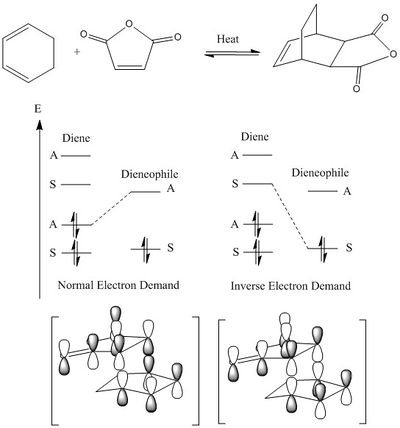 |
|---|
| Figure 65. Reaction scheme, qualitative energy level diagram and expected orbital overlap for the exo transition state structure. |
The geometry of maleic anhydride and modified bicyclo[2.2.2]oct-2-ene was orientated appropriately and optimised at the SE AM1 TS(Berny) level; from which, and energy of -0.05041984 Hartrees was obtained and the structure in figure 66. The difference in energy between the endo and exo transition state structures was determined to be 0.68 kcal/mol, which suggests that secondary orbital overlap and a less steric congestion in the transition state results in the endo being more stable.
(Perhaps expand this section out to explain the difference in steric congestion Tam10 (talk) 15:13, 23 February 2016 (UTC))
| Figure 66. Exo transition state structure. |
Figure 67 displays the imaginary vibration associated with the transition state, which occurred at -812.17 wavenumbers in a concerted manner.[15]
Visualisation of the appropriate computed MO's was undertaken and displayed in figures 68 through 71. It is evident, from these figures, that a of small degree secondary orbital overlap occurs, which was unexpected. The extent of the overlap is small however, and so can probably be ignored.
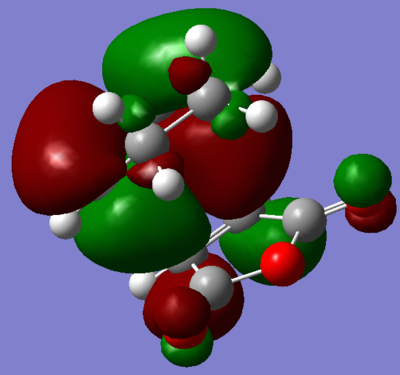 |
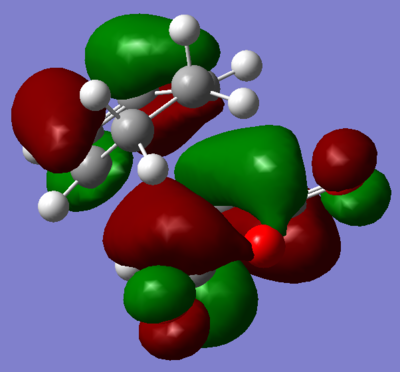 | |
| Figure 68. HOMO of transition state. | Figure 69. LUMO of transition state. | |
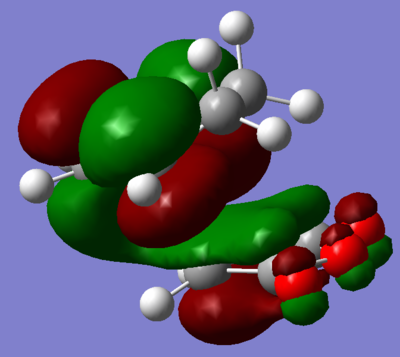 |
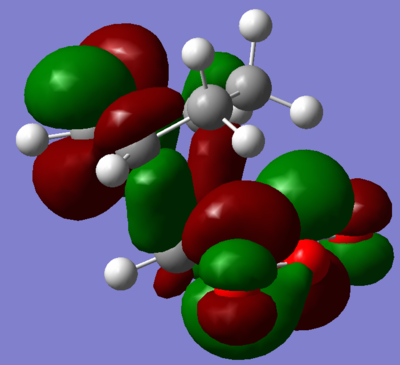 | |
| Figure 70. LUMO +1 of transition state. | Figure 71. LUMO +2 of transition state. |
Table 21 summarises the same bond lengths that were obtained for the endo transition state, but these values correspond to values obtained from the exo transition state. A comparison can be made to the endo transition state, for which table 18 summarises the obtained CC distances, which can be seen to be fairly similar.
| Bond | CC Bond lengths / nm |
|---|---|
| Partial | 2.17038 |
| Alkene - A | 1.39678 |
| Allyl - A | 1.39437 |
| Pre-Allyl - A | 1.48978 |
| Alkyl - A | 1.52206 |
| Alkene - B | 1.41011 |
| (CO)O(CO) - B | 2.27965 |
| Table 21. Summary of obtained CC bond distances for the endo transition state structure. | |
Thermochemical data was obtained for the exo transition state and displayed in table 22.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 22. Summary of obtained thermochemical data for the exo transition state at the SE AM1 level. | |||
Figure 72 displays the obtained IRC, which has a similar general appearance to that seen for endo, with the major difference being the direction of the calculation.
As seen with the endo transition state structure, bond formation is concerted. Figure 73 displays the animated IRC for which this observation was deduced.
Optimisation of the first frame from the IRC was performed and displayed in figure 74; the energy from which was found to be -0.15990921 Hartrees.
| Figure 74. Optimised final frame from IRC at the SE AM1 level. |
From inspection of figure 74, it can be seen that the maleic anhydride is in close proximity to the methylene hydrogens. Unfavourable van de Walls forces could arise from this geometry, which would result in a strained geometry. An energy difference between the endo and exo product was found to be 0.16 kcal/mol, with the former being more stable. As the exo product tends to be considered as the thermodynamically more stable product, the interaction between the methylene hydrangeas and maleic anhydride must be significant.
Table 23 displays the obtained thermochemical data, at numerous temperatures, for the exo transition state structure at the SE AM1 level.
| Parameter | Energy / Hartrees (298.15 K) | Energy / Hartrees (0.01 K) | Energy / Hartrees (400 K) |
|---|---|---|---|
| Sum of electronic and zero-point energy | |||
| Sum of electronic and thermal energies | |||
| Sum of electronic and thermal enthalpies | |||
| Sum of electronic and thermal free energies | |||
| Table 23. Summary of obtained thermochemical data for product from the exo transition state at the SE AM1 level. | |||
An activation energy of 28.57 kcal/mol for the exo transition state at 298.15 K. It is evident that the calculated value is not in good agreement with literature, which has a value of 11.4 kcal/mol.[21] From comparison to the previous section, it is evident that the endo transition state requires less energy to be obtained than exo.
Diels-Alder Conclusions
To summarise, it was found that the transition state for Diels-Alder reactions was relatively easy to probe computationally. Furthermore, the obtained structures, vibration and IRC for the transition state was in accordance with what was expected. Not all of the measurements obtained were in good agreement with literature, however. It was found that the activation energy was not predicted to a high degree of precision.
It was found that secondary orbital overlap can influence the stability of the transition state for more complicated Diels-Alder cycloadditions. However, this was not the only interaction that needed to be considered to explain the obtained energies. Overall, it was found that the endo transition state and product were more stable than the exo.
To improve on these calculations, structures should be optimised at a higher level, such as B3LYP/6-31G(d). This level was found to be the most accurate out of the sampled levels, from the relatively good comparison in bond lengths and activation energies to literature, which is why it has been suggested.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 J. Clayden, N. Greeves, S. Warren, Organic Chemistry, Oxford University Press, second edition, 2001, 34.
- ↑ P. von R. Schleyer, J. Am. Chem. Soc., 1957, 79, 12
- ↑ 3.0 3.1 R. B. Woodward, R. Hoffmann, Angew. Chem. Int. Ed., 1969, 8(11), 781-932.
- ↑ 4.0 4.1 4.2 G. D. Hammond, J. Am. Chem. Soc., 1955, 77 (2), 334–338
- ↑ 5.0 5.1 5.2 F. Jensen, Introduction to Computational Chemistry, Wiley, second edition, 2007.
- ↑ A. C. Cope, E. M. Hardy, J. Am. Chem. Soc, 1940, 62(2), 441-444.
- ↑ J. Clayden, N. Greeves, S. Warren, Organic Chemistry, Oxford University Press, second edition, 2001, 35.
- ↑ 8.0 8.1 8.2 8.3 B. W. Gung, Z. H. Zhu, R. A. Fouch, J. Am. Chem. Soc., 1995, 117(6), 1783-1788.
- ↑ 9.0 9.1 Y. Umezawa, S. Tsuboyama, H. Takahashi, J. Uzawa, M. Nishio, Tetrahedron, 1999, 55, 10047-10056S.
- ↑ 10.0 10.1 K. B. Widberg, M. A. Murcko, J. Am. Chem. Soc., 1988, 110, 8029-8038.
- ↑ B. G. Rocque, J. M. Gonzales, H. F. Schaeffer III, Mol. Phys., 2002, 100(4), 441-446.
- ↑ G. Schultz, I. Hargittai, J. Mol. Struct., 1995, 346, 63-69.
- ↑ 13.0 13.1 O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10336-10337.
- ↑ 14.0 14.1 P. W. Atkins; J. De Paule, Atkins’ Physical Chem- istry, Oxford University Press, ninth edition, 2010, chapter 12, 462-463.
- ↑ 15.0 15.1 15.2 15.3 15.4 K. M. Morgan, Annu. Rep. Prog. Chem., Sect. B, 2002, 98, 293–316.
- ↑ F. A. cary, R. J. Sandberg, Advanced Organic Chemistry Part A: Structure and Mechanisms, Springer, 2007.
- ↑ S. Fleming, G. R. Hart, P. B. Savage, J. Chem. Educ., 2000, 77, 790.
- ↑ N. K. V. Monteiro, C. L. Firme, World Journal of Chemical Education., 2015, 3, 6, 141-149.
- ↑ D. Rowley, H. Steiner, Discuss. Faraday Soc. 1951, 10, 198-213.
- ↑ C-H Huang, L-C Tsai, W-P Hu, J. Phys. Chem. A, 2001, 105 (43), 9945–9953.
- ↑ 21.0 21.1 R. A. Grieger, C. A. Eckert, J. Am. Chem. Soc., 1970, 92(24), 7149-7153.