Rep:Mod:Yunzhang Module3 Physical
Module3, Experiment 3: The Transition State
In this experiment, the transition state structures in larger molecules for Cope rearrangement and Diels Alder cycloaddition reactions are studies using molecular orbital-based computaional methods which solve the Schrodinger equation numerically and locate the transition state structures based on the local shape of a potential energy surface. It also gives us information about the shapes of the transition structures, the pathways in which the reaction undergoes and how big the barrier heights are.
The Cope Rearrangement Tutorial
Chemical reactivity of the Cope rearrangement of 1,5-hexadiene
Objectives:
locate the low-energy minima and transition structures on the C6H10 potential energy surface and determine the preferred reaction mechanism.
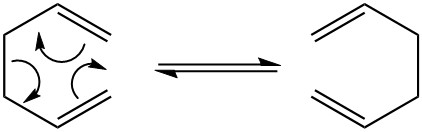
The [3,3]-sigmatropic shift rearrangement occurs in a concerted fashion(6 electrons; 4n+2; heat)via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy. The B3LYP/6-31G* optimisation was carried by using Gaussian and see how it matchees with this result.
| Cope rearrangement | Chair Transition State | Boat Transition State |
|---|---|---|
 |
 |
 |
Optimizing the Reactants and Products
(a) Open GaussView -> in the Molecule window: draw 1,5-hexadiene with an "anti" linkage for the central four C atoms -> click "Clean" under the "Edit" menu. "Calculate" -> "Gaussian" -> "Job type": optimization -> "Method": Hartree-Fock -> "Basis set": 3-21G -> "Link 0": %mem=250MB -> Submit -> save as "yun_react_anti" -> after job has finished, open the file -> Select "Yes" -> Files of type: choose *.chk -> Open "yun_react_anti" in the C:\Windows\G03\Scratch folder -> "Result": Summary -> "Edit": Symmetrize.
| 1,5-hexadiene with an "anti" linkage
for the central four C atoms |
Results Summary | |||
|---|---|---|---|---|
|
 |
The structure is the same one as Anti 3 in Appendix 1
(b) Draw 1,5-hexadiene with a "gauche" linkage for the central four C atoms and optimize the structure at the HF/3-21G level of theory.
Would you expect this structure to have a lower or a higher energy than the anti structure you have just optimized?
Both gauche and anti conformers are very similar in enenrgy; if the electrostatic effect(eg. gauche effect) overweighs the steric effect, the gauche conformers are preferred and vice versa.
| 1,5-hexadiene with a "gauche" linkage
for the central four C atoms |
Results Summary | |||
|---|---|---|---|---|
|
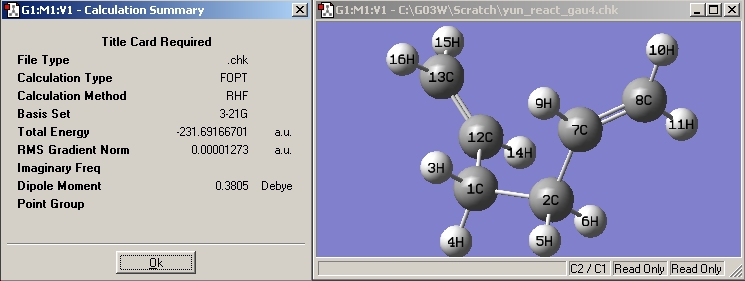 |
The structure is the same one as Gauche 4 in Appendix 1
(c)-(e) Based on the results above, predict the lowest energy conformation of 1,5-hexadiene and test out your hypothesis by drawing the structure and optimizing it.
The gauche conformer for 1,5-hexadiene is more stable than that of the anti conformer from thre optimisation above; in the hypothesis test, all the gauche and anti conformers have been optimised at HF/3-21G level of theory. The names of the structure optimized are given by the matching structure in [Appendix 1]. Hypothesis test:
| Gauche conformer | Jmol | Results Summary | |||
|---|---|---|---|---|---|
| Gauche1 |
|
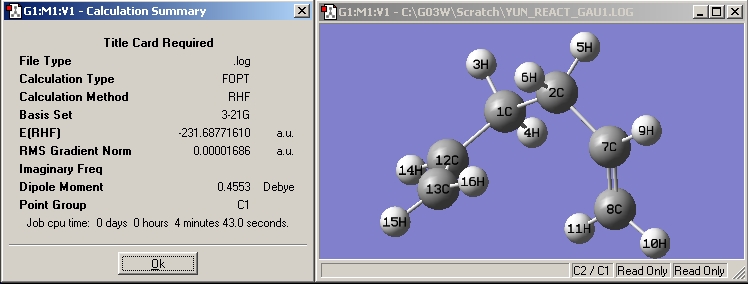 | |||
| Gauche2 |
|
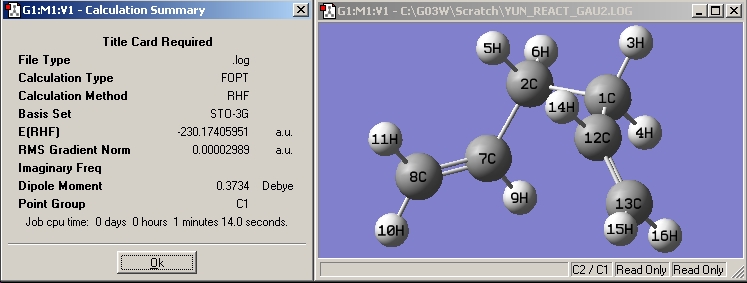 | |||
| Gauche3 |
|
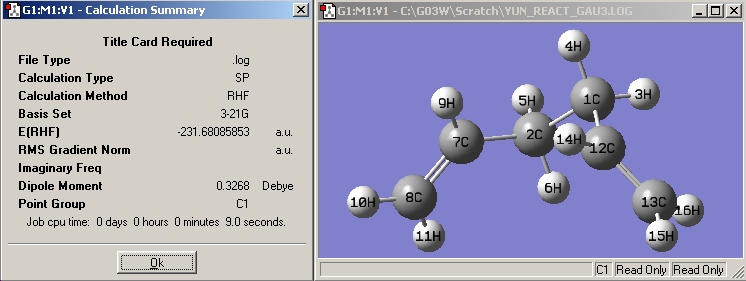 | |||
| Gauche5 |
|
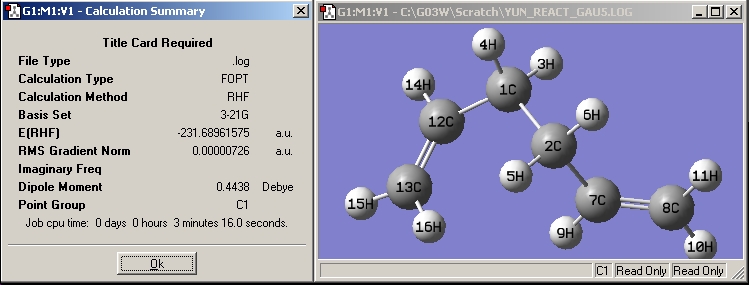 | |||
| Gauche6 |
|
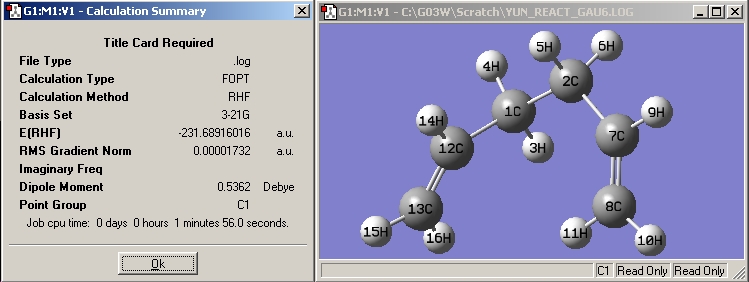 |
| Anti conformer | Jmol | Results Summary | |||
|---|---|---|---|---|---|
| Anti1 |
|
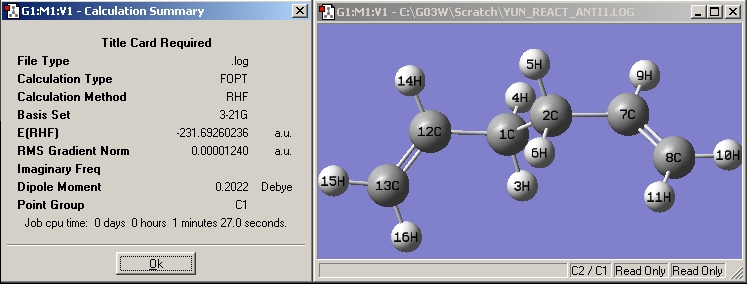 | |||
| Anti2 |
|
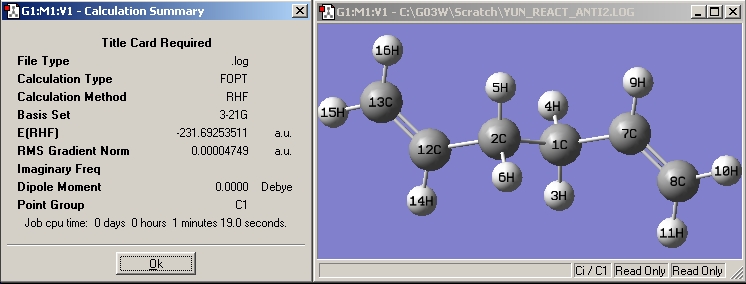 | |||
| Anti4 |
|
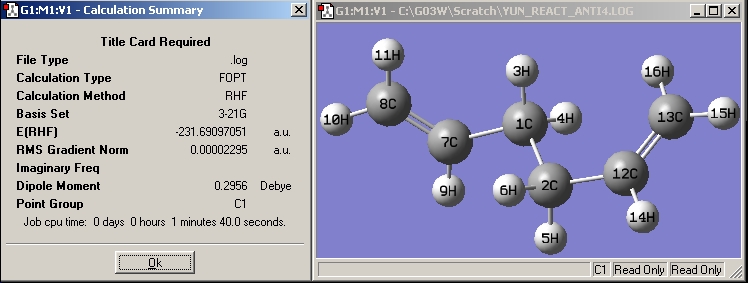 |
The energy obtained for each conformer is well matched with the ones shown in [Appendix 1] which conforms the optimisation has been carried out correctly.
(f) The structures are reoptimized at the B3LYP/6-31G(d)level:
| Gauche conformer | Jmol | Results Summary | |||
|---|---|---|---|---|---|
| Gauche1 |
|
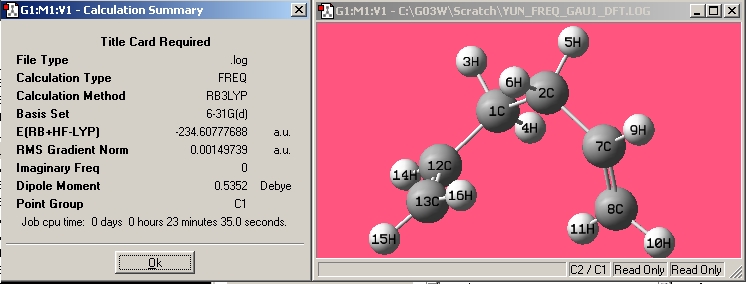 | |||
| Gauche2 |
|
 | |||
| Gauche3 |
|
 | |||
| Gauche4 |
|
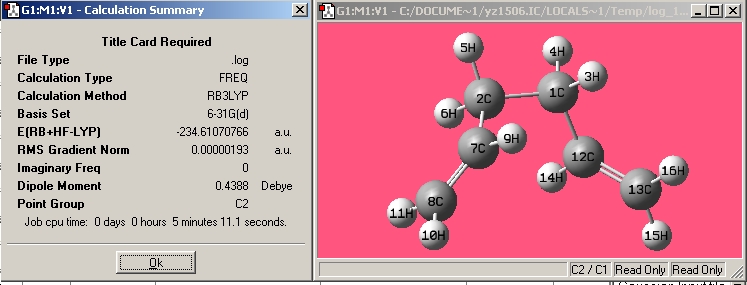 | |||
| Gauche5 |
|
 | |||
| Gauche6 |
|
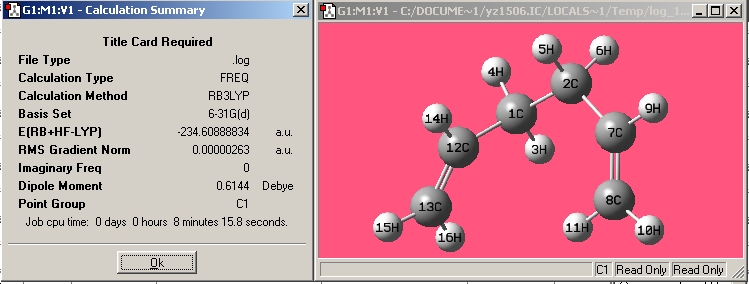 |
| Anti conformer | Jmol | Results Summary | |||
|---|---|---|---|---|---|
| Anti1 |
|
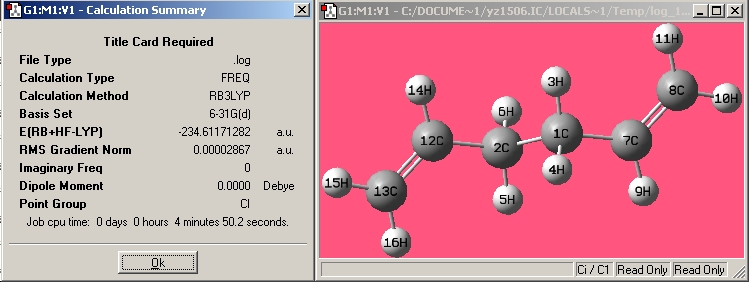 | |||
| Anti2 |
|
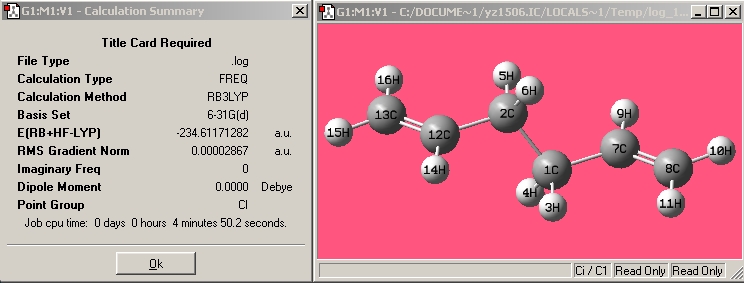 | |||
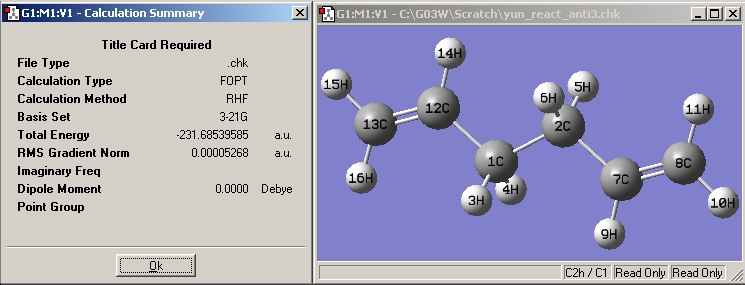
| Anti3 |
|
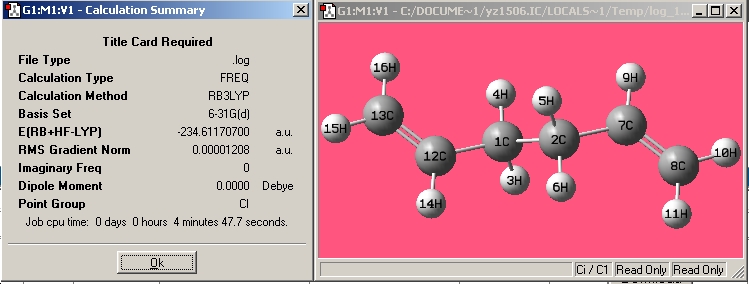 | |||
| Anti4 |
|
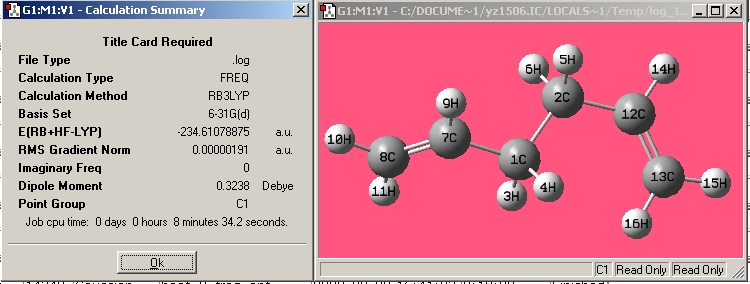 |
Compare the final structures from the HF/3-21G calculation with that at the higher level of theory. How much does the overall geometry change?
There is no significant change in geometry and all the point group stays the same for for all the conformers when a higher level of optimization is carried out. However the energy is minimized further when the B3LYP/6-31G(d) level of theory is applied. Geometric information under B3LYP/6-31G and B3LYP/6-31G(d) methods:
(g) Open the optimized B3LYP/6-31G(d) structure -> Calculate: Gussian -> Job type: Frequency -> Method: DFT; B3LYP/6-31G(d) -> link 0: yun_freq_gau1_DFT.chk -> save -> run -> Once the job has finished, open yun_freq_gau1_DFT.log -> Results menu: Vibrations -> Check there are only real frequencies -> Spectrum.
There is no imaginary vibrational frequencies for all the structures as shown in the B3LYP/6-31G(d) result summary table, this means that a minimum energy is obtained for all the structures.
On Results menu: View File -> find Thermochemistry -> find Vibrational temperatures: a list of energies -> Make a note of (i) the sum of electronic and zero-point energies(E = Eelec + ZPE); (ii) the sum of electronic and thermal energies(E = E + Evib + Erot + Etrans); (iii) the sum of electronic and thermal enthalpies(H = E + RT); (iv) the sum of electronic and thermal free energies(G = H - TS).
Results:
| Name of structure | Energy data |
|---|---|
| Gauche1 |  |
| Gauche2 |  |
| Gauche3 |  |
| Gauche4 |  |
| Gauche5 |  |
| Gauche6 |  |
| Anti1 |  |
| Anti2 |  |
| Anti3 |  |
| Anti4 |  |
Optimizing the "Chair" and "Boat" Transition Structures
Optimizing the "Chair" Transition Structures
(a) Draw a planar allyl fragment(CH2CHCH2)-> run a HF/3-21G level optimisation -> copy this structure to a new GaussView window
twice and orient for them to look like the chair transition state (translate one fragment: Shift Alt keys + Left Mouse button;
rotate: Alt key + Left)-> Bond distance between the terminal Cs of the CH2CHCH2 fragments ~ 2.2 Å -> Save as chair_ts_guess.
(b) Use Hartree Fock and the default basis set 3-21G for parts (b) to (f).
Optimization by using Hessian:
File → New → Create MolGroup -> copy and paste the guess structure into the window -> Calculation: Gaussian -> Job Type:
Opt+Freq; Optimization to a: TS (Berny); calculate force constants: Once; Additional keyword: Opt=NoEigen -> Submit.
After the job completes, it gives an imaginary frequency -817.897cm-1 due to the Cope rearrangement.
Optimization by using Frozen coordinate:
(c) Frozen coordinate optimization: File → New → Create MolGroup -> copy and paste the guess structure into the window ->
Edit: Redundant Coord Editor -> click on Create a New Coordinate -> On GaussView window: select 2 of the terminal Cs from the
CH2CHCH2 fragments which form/break a bond during the rearrangement -> On coordinate editor: select Coordination: Bond; Freeze
Coordinate -> Set value: 2.2 -> click on Create a New Coordinate -> select the opposite 2 terminal Cs -> select Bond and Freeze
Coordinate -> Click OK -> Submit.
(d) Open the file after the job has finished -> Edit: Redundant Coord Editor -> create a new coordinate by clicking on Create
a New Coordinate -> Select one of the bonds that was frozen before -> Coordinative: Bond; Derivative -> Repeat this procedure for
the other bond -> Calculate: Gaussian -> Job type: opt+freq; optimize to a: TS(Berny); Calulate Force Constants: Never ->
yun_opt_freq_redundant2 -> submit. This transition structure gives an imaginary frequency -817.947cm-1 due to the Cope rearrangement.
Results:
Optimizing the "Boat" Transition Structures
(e) Optimization by using the QST2 method:
Open the chk file of anti2 -> open a second window -> create a new MolGroup -> copy anti2 molecule into the new window
and select File → New → Add to MolGroup(the original molecule disappears and a green circle appearwith a 2 next to
it -> copy and paste the reactant molecule again and we are going to make it the product molecule -> click on the
icon showing two molecules side by side -> View: select Labels and change the numbering.
Set up the 1st QST2 optimization:
On Gaussian menu -> Job Type: Opt+Freq; optimize to a: TS (QST2)-> Submit -> job fails.
 |
 |
The structure looks like chair transition state but with bonds more dissociated, this is because the calculation translated the top CH3CH2CH3 fragment but did not rotate it around the central bonds. |
|---|
| Set up your QST2 calculation again by going back to the original input file and this time
modify the geometries of both molecules, for the reactant, make the central C-C-C-C dihedral angle 0 and the inside C-C-C angle 100. Repeat for the product molecule. |
 |
|---|
The QST2 calculation was then carried out.
Results:
| Jmol of the boat transition state under QST2 method | Result summary | Imaginary vibration | Advantage and disadvantage of using the QST2 method | |||
|---|---|---|---|---|---|---|
|
 |
 |
The QST2 method is easy to set up because it is fully automated, however the job has failed for serveal times before the correct optimisation was obtained due to the input guess transition structure is not close enough to the real one. |
Optimization by using the QST3 method:
Result:
| Input image | Result Summary and Imaginary vibration | Advantage of using the QST3 method |
|---|---|---|
 |
 |
The QST3 method is more reliable and the optimization is successfully carried out in one go. |
(f) The Intrinisic Reaction Coordinate/IRC plots a series of points by taking small geometric steps follow the direction in which the gradient is the steepest on the PE surface and this gives rise to the reaction path after the transition state.
Open optimized chair/boat transition structures -> Calculate: Gaussian -> Job Type: IRC; forward; once; 50 -> Submit. Since the RMS gradient has not reached a minimum yet, the follwing methods are used in order further minimize it: (1) Copy and paste structure 51 obtained in IRC to a new molgroup and run a normal minimization; (2) Carry out IRC as the one above with number of points=200; (3) Redo the IRC and choose force constants: always.
Results obtained by using three different methods above:
| Boat TS | Method 1 | Method 2 | Method 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jmol of the final structure obtained |
|
|
| |||||||||
| Result summary |  |
 |
 | |||||||||
| IRC |  |
 |
 | |||||||||
| Comment | Min. E= -231.69266121 a.u.
Point group= C1 fastest/ end up in the wrong minimum if the starting structure is not close enough to a local minimum |
Min. E= -231.69194563 a.u.
Point group= C1 more reliable/ too many points may veer off in the wrong direction therefore end up wit the wrong minimum; |
Min. E= -231.69266113 a.u.
Point group= C1 the most reliable/ the most expensive and may not be feasible for large molecules. |
| Chair TS | Method 1 | Method 2 | Method 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jmol of the final structure obtained |
|
|
| |||||||||
| Result summary |  |
 |
 | |||||||||
| IRC |  |
 |
 | |||||||||
| Comment | Min. E= -231.69166698 a.u.
Point group= C2 fastest/ end up in the wrong minimum if the starting structure is not close enough to a local minimum |
Min. E= -231.69164474 a.u.
Point group= C2 more reliable/ too many points may veer off in the wrong direction therefore end up wit the wrong minimum; |
Min. E= -231.69166674 a.u.
Point group= C2 the most reliable/ the most expensive and may not be feasible for large molecules. |
Conclusion: By using different approaches, the symmetry obtained for each is the same, C1 for the Boat structure and C2 for the Chair structure; the Boat structure obtained matches well with Gauche 3 whereas the Chair structure matches well with the Gauche 2, this tells us the conformers involved in the cope rearrangement; the energy obtained for the Boat structure is always lower than that of the chair in regardless of the method used, which indicates the Boat structure is the thermodynamically preferred structure.
(g)Calculate the activation energies for the reaction via both transition structures:
start from the HF/3-21G optimized structures -> carry out opt+freq for both chair and boat transition structures using B3LYP/6-31G(d).
1 Hartree= 627.509 391 kcal/mol therefore:
| / | Jmol | Results summary | ΔE under B3LYP/6-31G(d) at 298.15K | Experimental ΔE at 0K | |||
|---|---|---|---|---|---|---|---|
| Chair |
|
 |
33.69 | 33.5±0.5 | |||
| Boat |
|
 |
42.23 | 44.7±2.0 |
Conclusion:
The calculated activation energies match well with the experimental ones and the energy for each conformer obtained under the HF/3-21G and B3LYP/6-31G(d) methods are quite different in regardless of their similarity in geometry. Therefore, the higher level optimization could carried out based on the result obtained from the lower level of optimization in order to be more time efficient.
Exercise: The Diels Alder Cycloaddition
In the Diels Alder reactions(6п electrons; Hueckel transition state; suprafacial ; heat), the dieneophile π orbitals is involved in forming a new σ bonds with the diene π orbitals. Depends on the number of π electrons involved in this process, the reaction happens in either allowed or forbidden stereospecific fashion.
The Diels-Alder reaction between ethylene and butadiene
In this exercise, the HOMO/LUMO of cis-butadiene interacts with the π/ π* of the ethylene to form two new bonding and anti-bonding MOs([4s + 2s]), and if the HOMO/LUMO of cis-butadiene interacts with the π*/π of ethylene, the reaction is allowed. This interaction can only happen when these orbitals have the same symmetry and overlap isiginificantly, oherwise, the reaction is forbbidden.
Exercise
Use the the AM1 semi-empirical molecular orbital method for these calculations (to start with).
i) Sketch cis butadiene in GaussView -> Calculate: Gaussian -> Job type: opt_freq -> Method: AM1 semi-empirical -> additional keywords: ‘pop=full’ -> Submit.
| Jmol of cis butadiene | Results summary | |||
|---|---|---|---|---|
|
 |
Plot the HOMO and LUMO of cis butadiene and determine its symmetry:
| / | HOMO | LUMO |
|---|---|---|
| Cis-butadiene | 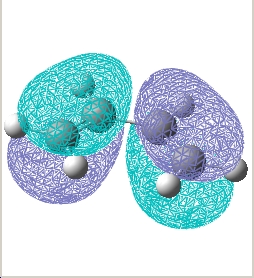 E= -0.343 a.u. |
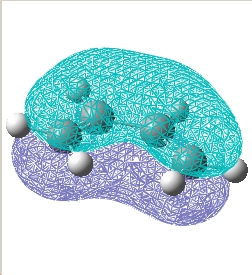 E= 0.017 a.u. |
| Symmetry w.r.t plane | Asymmetric | Symmetric |
The abve procedures have been repeated for ethylene:
| Jmol of ethylene | Results summary | |||
|---|---|---|---|---|
|
 |
Plot the HOMO and LUMO of ethylene and determine its symmetry:
| / | HOMO | LUMO |
|---|---|---|
| Ethylene | 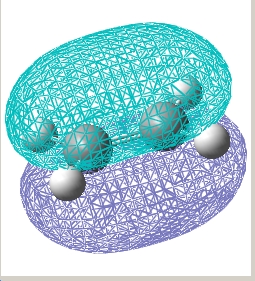 E= -0.387 a.u. |
 E= 0.052 a.u. |
| Symmetry w.r.t plane | Symmetric | Asymmetric |
ii) Computate the Transition State geometry and examine the nature of the reaction path for the prototype reaction.
Based on the optimisied structures in i) -> draw a guess transition state structure(the guessed interfragment distance between the chain end Cs= 2.1A) -> Calculate: Gaussian -> Job type: opt+freq; optimise to a: TS(Berny); calculate force constants: once -> Method: AM1 semi-empirical -> additonal keywords ‘opt=noeigen’. The optimization was successfully carried out as the output gives only one imaginary vibraitonal frequency.
| Jmol of Transition State geometry | Results summary | Imaginary frequency | |||
|---|---|---|---|---|---|
|
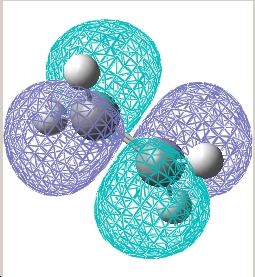
 |
 -955.785cm-1 |
As can be seen the transition structure has an envelope-like shape, since the overlap between the ethylene π/π* orbitals and the HOMO/LUMO of butadiene can be maximized.
Plot the HOMO and LUMO of transition structure and determine its symmetry:
The plane is defined by the horizental middle plane between the cis butadiene and the ethylene
| / | HOMO | LUMO |
|---|---|---|
| Transition state | 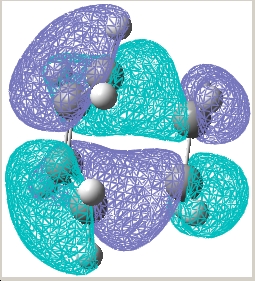 E= -0.323 a.u. |
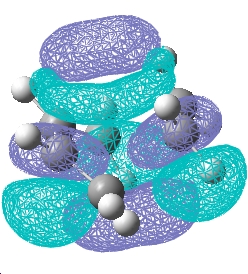 E= 0.023 a.u. |
| Symmetry w.r.t the plane | Asymmetric | Symmetric |
The reaction is allowed as a result of the asymmetric HOMO of cis-butadiene and the asymmetric LUMO of ethylene overlap to give a asymmetric transition state structure.
(iii) Study the regioselectivity of the Diels Alder Reaction between cyclohexa-1,3-diene and maleic anhydride.
As the reaction is controlled kinetically, the cyclohexa-1,3-diene undergoes facile reaction with maleic anhydride to give the endo adduct(transition state energy).
Results for Endo and Exo products:
| Jmol of Endo product | Results summary under HF/3-21G | Results summary under B3LYP/6-31G(d) | Geometric information(HF/3-21G) | Geometric information(B3LYP/6-31G(d)) | |||
|---|---|---|---|---|---|---|---|
|
 |
 |
 |
 |
| Jmol of Exo product | Results summary under HF/3-21G | Results summary under B3LYP/6-31G(d) | Geometric information(HF/3-21G) | Geometric information(B3LYP/6-31G(d)) | |||
|---|---|---|---|---|---|---|---|
|
 |
 |
 |
 |
Results for Endo and Exo tansition states:
| Jmol of Endo transition state | Results summary | Geometric information | Imaginary frequency | |||
|---|---|---|---|---|---|---|
|
 |
 |
 -805.614cm-1 |
| Jmol of Exo transition state | Results summary | Geometric information | Imaginary frequency | |||
|---|---|---|---|---|---|---|
|
 |
 |
 -811.515cm-1 |
Results for the HOMO/LUMO for the Exo and Endo Transition state:
| / | HOMO | LUMO |
|---|---|---|
| Endo | 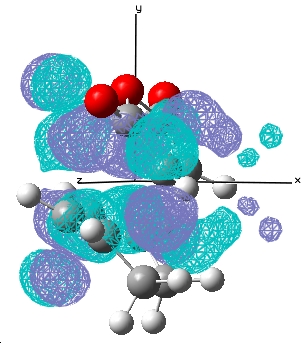 E= 0.028 a.u. |
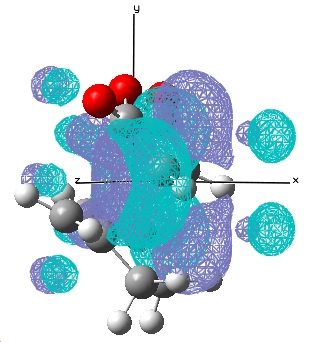 E= -0.020 a.u. |
| / | HOMO | LUMO |
|---|---|---|
| Exo | 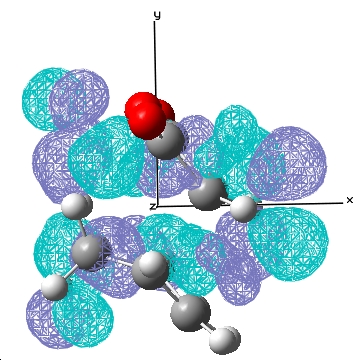 E= 0.033 a.u. |
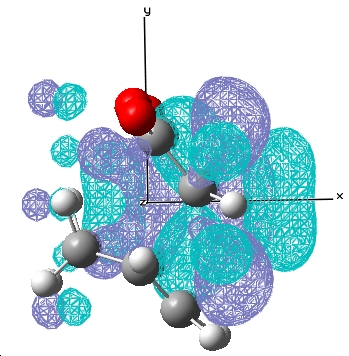 E= -0.020 a.u. |
- What can you conclude about the so called “secondary orbital overlap effect”?
Ian Fleming's book 'Frontier Orbitals and Organic Chemical Reactions').
- What are typical sp3 and sp2 C-C bondlengths? What is the van der Waals radius of the C atom? What can you conclude about the C-C bondlength of the partly formed σ C-C bonds in the TS.
- Is the formation of the two bonds synchronous or asynchronous? How does this compare with the lowest positive frequency?
The formaion of the two bonds are synchronous and .......
For the cyclohexa-1,3-diene reaction with maleic anhydride:
the exo form is more strained because the bridging and the -C=O-CO-C=O- fragment are pointing in the same direction whereas in the endo form, they are pointing in opposite direction.
Only one major nodal plane has been observed in the HOMO between the -C=O-CO-C=O- fragment and the remainder of the system.
Further discussion: What effects have been neglected in these calculations of Diels Alder transition states?