Rep:Mod:YuhanJin
NH3
Data Summary After Optimization
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient Norm | 0.00000485 a.u. |
| Point Group | C3V |
| Bond Length N-H | 1.01798 Å |
| Bond Angle H-N-H | 105.741 degrees |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000070 0.001800 YES
RMS Displacement 0.000033 0.001200 YES
Predicted change in Energy=-5.785202D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
For more information about the summary of optimised NH3, please click here.

NH3 |
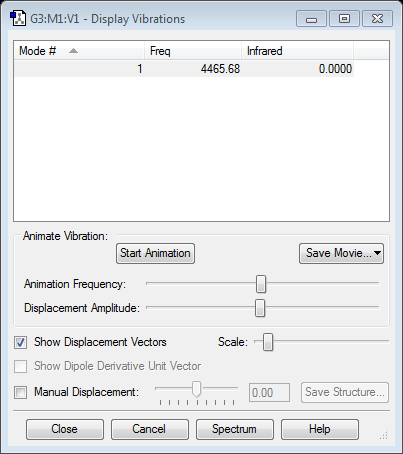
Vibrations
There are 6 modes. The two pairs of modes are degenerate, with frequency 1693.95 and 3589.82. These pairs are highly symmetric. The first three modes are 'bond bending' because the bond angles change. The last three modes are 'bond stretching' due to higher frequency, which is equivalent to higher energy. Mode 1 is called as 'umbrella' mode. Three bands will occur in experimental spectrum of gaseous ammonia
Charges
The charges on N atom is -1.125 and on all four H atom are +0.375. The N atom is much more electronegative than H atoms so the electrons that the whole molecule obtains are distributed more closely to N atom. Therefore, N atom is more negatively charged.
N2
Data Summary After Optimization
Calculation Method is RB3LYP.
Basis Set = 6-31G(d,p)
Final Energy E(RB3LYP) = -109.52412868 a.u.
RMS Gradient Norm = 0.00000060 a.u.
Point Group = D*H
Bond Length N-N: 1.09200 Å
Bond Angle H-N-H: 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.383733D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
For more information about the summary of optimised N2, please click here.
N2 |
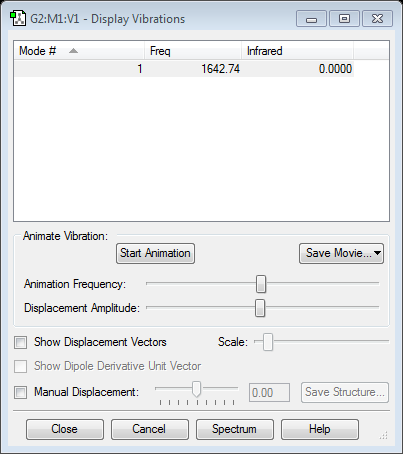
Vibration
 There is only stretching mode.
There is only stretching mode.
H2
Data Summary After Optimization
Calculation Method is RB3LYP.
Basis Set = 6-31G(d,p)
Final Energy E(RB3LYP) = -1.17853936 a.u.
RMS Gradient Norm = 0.00000017 a.u.
Point Group = D*H
Bond Length H-H: 0.60000
Bond Angle H-H: 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.167771D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
For more information about the summary of optimised H2, please click here.
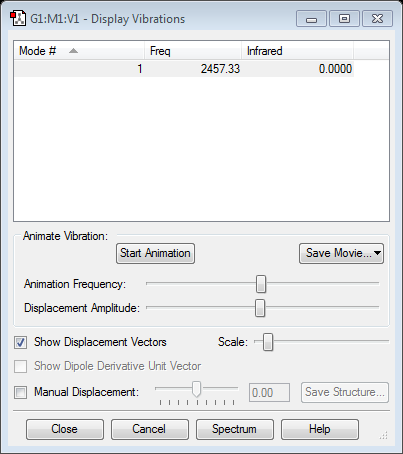
H2 |
Vibration
Haber-Bosch process
The reaction formula is
N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.1155375 a.u. -(-109.52412868 a.u.)+(-3.53561808 a.u.) = -7.1272872 a.u. = -18712.6939691kJ/mol
Since ΔE is negative, the forward reaction is exothermic, which means the gaseous reactants have higher energy. Therefore, the ammonia product is more stable.
O2
Data Summary After Optimization
Calculation Method is RB3LYP.
Basis Set = 6-31G(d,p)
Final Energy E(RB3LYP) = -150.25250603 a.u.
RMS Gradient Norm = 0.05905207 a.u.
Point Group = D*H
Bond Length O-O: 1.16160 Å
Bond Angle O-O: 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000130 0.000450 YES
RMS Force 0.000130 0.000300 YES
Maximum Displacement 0.000080 0.001800 YES
RMS Displacement 0.000112 0.001200 YES
Predicted change in Energy=-9.882886D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.216 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
For more information about the summary of optimised O2, please click here.
O2 |
Vibrations
There is a sigma bond and a pi bond between two oxygen atoms. The only mode of vibration of O2 is stretching bond.
Charges
The O2 molecule is neutral. The electrons are evenly distributed between two oxygen atoms. The dipole moment is all zero.
Molecular Orbitals
1s orbitals are much deeper than the 2s orbital. From the figure for energy, we can see that 1s orbitals are located at -19 a.u. approximately while the 2s orbitals start from around -1 a.u. This explains why 1s orbitals are usually not considered in molecular orbitals except small atoms.

Figure.1 shows 3rd garade sigma bonding. It is mixed by head-on overlapping of two 2p orbitals contributed by each oxygen atom. The MO is constructive as they combine in phase linearly. It is fully occupied and lower in energy(around -0.53) than HOMO region.
Since there are three dumbbell-shape orbitals lying on each axis of x,y and z, one of overlapping is head-on(forming sigma bond) and the other two should be side-away(forming pi bond).


Figure.2 and Figure.3 MO diagrams demonstrate the first(the lowest energy) ungarade pi bonding. One is combined by overlapping side-aways of two 2p orbitals above or below x-y plane and the other is mixed above or below x-z plane. Even though the two halves are in different color, in fact, the 2p orbitals are combined in phase and the MO is constructive. It is occupied fully. Pi bond strengthens the bonding between two oxygen atoms as it is not simply a one-dimension bond.
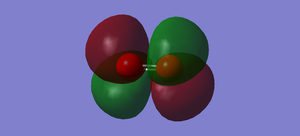
Similarly with ungarade pi bonding, garade pi antibonding occurs as a pairs. Only one mode is chosen to be shown in Figure.4. The color of electron density is same diagonally which means 2p orbitals are mixed out of phase. Therefore, the MO is destructive, leading to the higher in energy than the corresponding pi bonding. Also, it is HOMO, the highest occupied orbitals. It interacts with other orbitals of other molecules when reaction takes place.

In Figure.5, it gives the 3rd ungarade sigma antibonding, which has the highest energy(0.212 a.u.) among MOs mixed by 2p orbitals. It is combined by two out-of-phase 2p orbitals linearly. As we can see from diagram, the electron density between two oxygen atoms is smaller than the outsiders because it is destructive.