Rep:Mod:YYTmod3

Year 3 Computational Lab Module 3

Yiting Ye

The Cope Rearrangement Tutorial

Cope reaction of 1,5-hexadiene

In this tutorial, the reaction mechanism of the [3,3]-sigmatropic shift rearrangement was studied using 1,5-hexadiene as an example. The reaction route that is currently accepted to go via either chair or boat form of transition state.

* Optimizing the Reactants and products

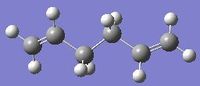
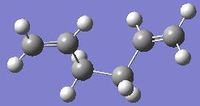
In GaussView, create a molecule of 1,5-hexadiene with an "anti" and "gauche" linkage for the four central carbon atoms in separate windows. The structures were shown as on the right.

These structures were firstly cleaned and optimized at the HF/3-21G level of theory.

HF/3-21G optimization result of 1,5-hexadiene
structure	Total energy / a.u.	Point Group
"anti"-linkage	-231.69260235	C₂
"gauche"-linkage	-231.69266120	C₁

These input structures were guessed to have the lowest energy. Their optimization were the same as structure A1 and G3 in Appendix 1, which had minimum energy for anti- and gauche- conformations respectively. The total energy calculated was also the same as those in the table.

The A2 structure were drawn in a new window of GaussView, and was optimized using HF/3-21. The total energy computed was the same as mentioned in Appendix 1. Then, the structure was re-optimized using DFT/B3LYP/6-31(G) combination.

optimization result of A2 Structure
Optimization Theory	Total energy / a.u.	Point Group
HF/3-21	-231.69253528	C_i
DFT/B3LYP/6-31(G)	-234.61169864	C_i

For the two methods, the point group of the structure kept unchanged, but the total energy calculated using DFT/B3LYP/6-31(G) was 2.91916338 a.u. (that is 7664.264038 kJ/mol) lower than that of HF/3-21. This energy change was quite significant though the two optimizations looked fairly alike.

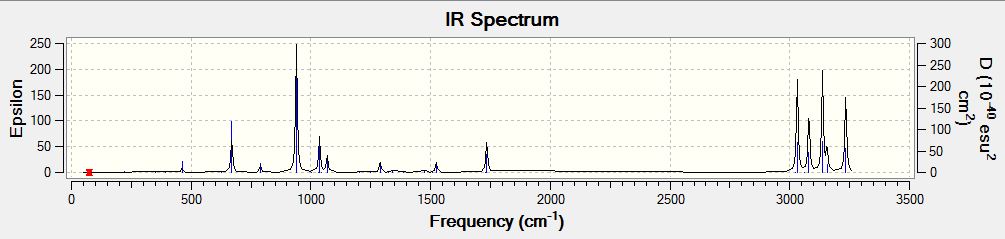
The last optimization was carried on to the frequency analysis. The total energy obtained from the vibrational calculation was -234.61171012 a.u., which was very close to the optimization one, and it proved the optimization was at minimum energy point. The vibrational frequencies were all positive, and the IR spectrum was shown as below:

In the .log file of the frequency analysis, the following energies were printed:

Sum of electronic and zero-point energies	234.469206 a.u.
Sum of electronic and thermal energies	234.461858 a.u.
Sum of electronic and thermal enthalpies	234.460914 a.u.
Sum of electronic and thermal free energies	234.500782 a.u.

Log file of "anti"-linkage 1,5-hexadiene

Log file of "gauche"-linkage 1,5-hexadiene

Log file of HF/3-21G optimization of A2

Log file of B3LYP/6-31G* optimization of A2

* Optimizing the "Chair" and "Boat" Transition Structures

a) Chair Transition State Optimization

An allyl fragment (CH₂CHCH₂) was drawn and optimized using HF/3-21G in Gaussview. This optimized fragment was then pasted two times in a new window, and oriented to a "chair" transition state as shown in Appendix 2 of the instruction. The chair transition state was firstly optimized using HF/3-21G to a TS(Berny). After that, coordinates of terminal carbons were frozen and the whole system was optimized to minimum using the same level of theory. When the job was finished, reoptimized it to transition state with previously frozen atoms being taken into account.

HF/3-21G Optimization Results of Chair Transition State
	Total Energy / a.u.	bond forming / bond breaking bond lengths
1st optimization	-231.61932244	2.02Å
2nd optimization	-231.61518508	2.20Å
3rd optimization	-231.61932197	2.02Å

All three optimized structures looked similar, especially the first and the last optimization. The second one had slightly larger total energy, and the bond forming/bond breaking bond lengths were a little longer.

Log file of 1st optimization of chair transition state

Log file of 2nd optimization of chair transition state

Log file of 3rd optimization of chair transition state

b) Boat Transition State Optimization

The optimized Ci reactant molecule was copied and pasted into a new window of GaussView. Another copy was pasted into another page of the same window. Then, these two geometries were oriented and re-numbered as reactant and product. After modification of geometries of the reactant and product closer to boat transition structure, optimization was run to TS(QST2).

Structure	Total Energy	Imaginaary Frequency	Vibrational Motion
	-231.60280225 a.u.	-840.14 cm^-1		Pair of carbon atoms forming/breaking bonds between them move toward and away from each other, with one pair moving in opposite direction of the other pair. The central carbon atoms move slightly towards the separationg terminal carbon pairs.

Log file of HF/3-21G optimization of boat transition state

c) Intrinisic Reaction Coordinate(IRC) Method

The IRC method can compute the minimum energy path from a transition structure down to its minimum on a potential surface. This gives clues of the conformation of product. In this part, the IRC of the chair transition structures were run. Since the first calculation had not reach the minimum geometries( gradient≠0 as shown in diagram on the right), the following three modifications were taken:(i)optimized the last point structure to minimum energy; (ii)restarted the IRC calculation with the number of points equaled 1000; (iii)redid the job choosing to compute the force constants at every step.

IRC Resulted Structures
Structure		Total Energy
		-231.68513658 a.u.
Modification		-231.69166702 a.u.
		-231.68513658 a.u.
		-231.69166423 a.u.

As shown in the table and diagrams above. Modification 1 and 3 led to slightly lower total energies (ΔE=17.1383kJ/mol) with the structure roughly unchanged. However, for method 2, the total energy stayed the same but the structure altered significantly. And the gradient plot showed that the structure had not reach minimum yet, though the last point gradient unchanged no matter the number of points was set to be 250, 500, or 1000 in the calculation.

Log file of IRC calculation of chair transition state

Log file of method 1 of IRC modification

Log file of method 2 of IRC modification

Log file of method 3 of IRC modification

d) Activation Energies Calculation

In this section, optimization at B3LYP/6-31G level of theory followed by frequency calculation was run for both HF/3-21G optimized chair and boat transition structures.

Result Comparison between Method HF/3-21G and B3LYP/6-31G*
Structure	Level of Theory of Optimization	Total Energy / a.u.	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Acitivation Energy (at 0K) / kcal mol^-1	Acitivation Energy (at 298.15K) / kcal mol^-1
Reactant (A2)	HF/3-21G	-231.69253528	-231.539539 a.u.	-231.532565 a.u.	-	-
Reactant (A2)	B3LYP/6-31G*	-234.61169864	-234.469206 a.u.	-234.461858 a.u.	-	-
Boat	HF/3-21G	-231.60280225	-231.450924 a.u.	-231.445296 a.u.	55.61	54.76
Boat	B3LYP/6-31G*	-234.54309298	-234.402340 a.u.	-234.396006 a.u.	41.96	41.32
Chair	HF/3-21G	-231.61932197	-231.466695 a.u.	-231.461336 a.u.	45.71	44.70
Chair	B3LYP/6-31G*	-234.55698282	-234.414931 a.u.	-234.409010 a.u.	34.06	33.16

The results calculated were very close to that provided in the instruction. As the experimental activation energies are 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure at 0 K, the B3LYP results were obviously closer to these experimental values, though it was 2.74±2.0 kcal mol^-1 lower via boat transition state but 0.56±0.5 kcal mol^-1 higher via chair transition state.

Log file of HF/3-21G frequency calculation of reactant

Log file of B3LYP/6-31G* frequency calculation of reactant

Log file of HF/3-21G frequency calculation of boat transition state

Log file of B3LYP/6-31G* frequency calculation of boat transition state

Log file of HF/3-21G frequency calculation of chair transition state

Log file of B3LYP/6-31G* frequency calculation of chair transition state

The Diels Alder Cycloaddition

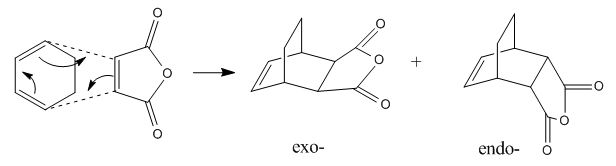
a) In this part, the reaction route of the following reaction was explored.

Firstly, a butadiene molecule was built in GaussView and optimized to minimum using AM1 semi-empirical molecular orbital method. After optimization, both HOMO and LUMO were calculated.

AM1 Optimization result for Butadiene
Structure	Total Energy	HOMO	LUMO
	0.0487918 a.u.	symmetry:a	symmetry:s

Next, the transition state was drawn in a new window. Since the forming bond lengths in literature were 2.26Å and 2.28Å (DOI:10.1021/ja00447a014 ), the terminal carbons were palced approximately 2.27Å apart. The whole system was then optimized to TS(Berny), with "opt=noeigen" in the "additional keyword" box. When the job was finished, the coordinates of four carbons were frozen with the bond lengths being set to be 2.2Å (2.3Å was tried but failed in the last calculation), and an optimization to minimum was run. After that, the resulted structure was again optimized to transition state. The AM1 semi-empirical molecular orbital method was used for all calculations in this step.

AM1 Optimization Results of Transition State
	Total Energy / a.u.	bond-forming bond lengths
	0.11165465	2.12Å
	0.10745390	2.20Å
	0.11165482	2.12Å

The three resulted structures were fairly alike. However, the second calculation, optimization to minimum with frozen terminal carbon coordinates, had slightly lower total energy whereas the other two had similar results.

The typical sp³ C-C bond length is 1.54Å, the typical sp² C-C bond length is 1.34Å (ref²), and the van de waals radius of carbon is 1.7Å (ref¹) The calculated partially formed C-C σ bond bond length was longer than those of both sp² and sp³ C-C bond, but shorter than two times of the van de waals radius of carbon. This meant there was an orbital overlap between the two carbons of the forming bond, but the overlap density was not so strong as that of an already formed C-C bond.

HOMO and LUMO of the 3rd Optimization of Transition state
	Molecular Orbital Computed	LCAO	Symmetry
HOMO			a
LUMO			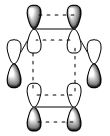s

The HOMO of the transition state has symmetry of a, and was formed by HOMO of butadiene and LUMO of ethylene. Since these two MOs had the same symmetry, a, they had significant overlap density and that allowed interactions between them.

A frequency analysis was run for the last calculation. The total energy computed was the same as that of the optimization. There was one vibration mode which had imaginary frequency. In the table below, this negative frequency vibration was compared with the lowest positive frequency vibration.

Frequency	Vibrational Motion
-955.87 cm^-1		The four terminal carbons is moving toward and away from each other along the partially formed C-C bond. The C=C bond is doing stretching motion, so that the bond elongates when the terminal carbons approaching the C=C carbons.
147.17 cm^-1		The two molecular fragments are rotating along the fragment centres in opposite directions.

The partially forming C-C σ bonds were stretching synchronously in the negative frequency vibration and rotating in the same order in the lowest positive frequency vibration. Therefore, these two forming bond could be considered to form at the same time as they were acting in the same way in these vibrational motions.

References

1. Encyclopedia of Distances, Michel M. Deza, Elena Deza, 2009, P437

2. Aieee Chemistry in 30 Days, Tmh, P21.2

3. Transition state of the Diels-Alder reaction, M. V. Basilevskii, A .G. Shamov, V. A. Tikhomirov, 1977 (DOI:10.1021/ja00447a014 )

Log file of optimization of butadiene

Log file of 1st optimization of transition state

Log file of 2nd optimization of transition state

Log file of 3rd optimization of transition state

Log file of frequency calculation 3rd optimization of transition state

b) After the study of the reaction route, the regioselectivity of the Diels Alder reaction was examed.

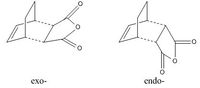
The exo- and endo- products of reaction between cyclohexa-1,3-diene and maleic anhydride were built in GaussView. These structures were cleaned and optimized to minimum. To alter the resulted product structures into transition states, the newly-formed C-C bonds were removed and the positions of the two fragments were adjusted to have a roughly 2.2Å bond forming bond lenght. Similar to the optimizations of the transition state in part (a), both structures underwent a three-step calculation: firstly optimized to TS(Berny), with "opt=noeigen" in the "additional keyword" box; then the coordinates of four bond forming carbons were frozen having the bond lengths set to be 2.2Å and optimizations to minimum were run; finally the resulted structure was again optimized to transition state. The AM1 semi-empirical molecular orbital method was used for all calculations in this task.

Energy / a.u.		Structure
Total Energy	-0.05041982	partially formed C-C σ bond lengths were 2.17Å; the other C-C distances were 1.39-1.52Å; the C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the "opposite" -CH₂CH₂- were 2.95Å.
Sum of electronic and zero-point energies	0.134880
Sum of electronic and thermal energies	0.144879
Sum of electronic and thermal enthalpies	0.145824
Sum of electronic and thermal free energies	0.099121
Total Energy	-0.05150479	partially formed C-C σ bond lengths were 2.16Å; the other C-C distances were 1.39-1.52Å; the C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the "opposite" -CH=CH- were 2.89Å.
Sum of electronic and zero-point energies	0.133494
Sum of electronic and thermal energies	0.143683
Sum of electronic and thermal enthalpies	0.144627
Sum of electronic and thermal free energies	0.097352

In the results of frequency calculations, both exo- and endo- structures had imaginary frequencies, -813.10 cm^-1 and -807.10 cm^-1 respectively. These vibrational motions were the same as that of the transition state in part (a), and the other atoms were stationary.

According to the results, the exo- structure had higher energies than the endo- one did (energy differences: 2.84kJmol^-1 for total energy, 3.64kJmol^-1 for sum of electronic and zero-point energies, 3.14kJmol^-1 for sum of electronic and thermal energies, 3.14kJmol^-1 for sum of electronic and thermal enthalpies, 4.64kJmol^-1 for sum of electronic and thermal free energies). This is resulted from both the second orbital overlap (SOO) effect and the group repulsion effect. SOO is defined as the positive overlap of a nonactive frame in the frontier molecular orbitals of a pericyclic reaction(DOI:10.1021/jo00384a016 ). The primary overlap involves orbital overlap between the bond-forming/bond-breaking carbons which is considered to be the active frame. In this section, the endo- structure had SOO between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the "opposite" -CH=CH-, and that stabilized the molecule. In contrast, the exo- structure had no SOO as the -CH=CH- in on the other side. Instead, there was repulsion between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the "opposite" -CH₂CH₂-.

Reference

1. Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies, Marye Anne Fox, Raul Cardona, Nicoline J. Kiwiet, 1987 (DOI:10.1021/jo00384a016 )

Log file of 1st optimization of exo- transition state

Log file of 2nd optimization of exo- transition state

Log file of 3rd optimization of exo- transition state

Log file of frequency calculation of 3rd optimization of exo- transition state

Log file of 1st optimization of endo- transition state

Log file of 2nd optimization of endo- transition state

Log file of 3rd optimization of endo- transition state

Log file of frequency calculation of 3rd optimization of endo- transition state