Rep:Mod:YX8818
NH3 molecule
Summary information
| molecule name | NH3 |
| N-H bond distance | 1.018 |
| H-N-H bond angle | 105.7 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D,P) |
| Final energy E(RB3LYP) in atomic units (au) | -56.5577687 a.u. |
| the point group | C3v |
"Item" section in the log file
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000070 0.001800 YES RMS Displacement 0.000033 0.001200 YES
JMol of structure
Ammonia molecule |
File:YX8818 NH3 OPTIMISATION.LOG
Snap shot of the display vibrations
Table of vibrations and intensities
| wavenumber cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| symmetry | A1 | E | E | A1 | E | E |
| intensityin arbitrary units | 145 | 14 | 14 | 1 | 0.3 | 0.3 |
| image |  |
 |
 |
 |
 |

|
| how many modes do you expect from the 3N-6 rule? | 6 |
| which modes are degenerate ? | The two bending modes at 1694 cm-1 are degnerate, and the two stretching modes at 3590 cm-1 are degenerate. |
| which modes are "bending" vibrations and which are "bond stretch" vibrations? | The to vibrations at 1090 and the one 1694 cm-1 are bending vibrations.
The vibrations at 3461 and two vibrations at 3590 cm-1 are stretching vibrations. |
| which mode is highly symmetric? | The modes at 1090 and 3461 cm-1 are highly symmetric. |
| one mode is known as the "umbrella" mode, which one is this? | The mode at 1090 cm-1 is known as the embrella mode. |
| how many bands would you expect to see in an experimental spectrum of gaseous ammonia? | 2 bands are expected. |
NBO charges
| N-atom | -1.125 |
| H-atoms | 0.375 |
A negative charge is expected for N because is more electronegative than H, hence it draws the electron density away from H. Hence H is expected to have a positive charge.
N2 molecule
Summary information
| molecule name | Nitrogen (N2) |
| N-N bond distance | 1.106 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) in atomic units (au) | -109.52412868 a.u. |
| the point group | D∞h |
"Item" section in the log file
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
JMol of structure
Nitrogen molecule |
File:YX8818 N2 OPTIMISATION.LOG
Snap shot of the display vibrations
Table of vibrations and intensities
| wavenumber cm-1 | 2457 |
| symmetry | SGG |
| intensity in arbitrary units | 0 |
| image | 
|
NBO charges
| N-atom | 0.000 |
H2 molecule
summary information
| molecule name | Hydrogen (H2) |
| H-H bond distance | 0.743 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) in atomic units (au) | -1.1785394 a.u. |
| the point group | D∞h |
"Item" section in the log file
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
JMol of structure
Hydrogen molecule |
File:YX8818 H2 OPTIMISATION.LOG
Snap shot of the display vibrations
Table of vibrations and intensities
| wavenumber cm-1 | 4466 |
| symmetry | SGG |
| intensity in arbitrary units | 0 |
| image | 
|
NBO charges
| H-atom | 0.000 |
Mono-metallic TM complex
unique identifier = BARTOF
N-N bond distance =1.112
(dinitrogen)-(2,6-bis(1-(2,6-diisopropylphenylimino)propyl)pyridine)-iron |
The N-N bond distance in the TM-complex is longer than that from the N2 (1.106). This maybe be due to the MOs on Nitrogen constructively interact with the orbitals on the TM-metal. This draws away electron density away from the N-N bonds, thus weakening the bond and makes the bond length longer.
The Haber-Bosch process
| Energy | Values in atomic units | Values in kJ/mol |
| E(NH3)= | -56.5577687 | -148492.4 |
| 2*E(NH3)= | -113.1155375 | -296984.8 |
| E(N2)= | -109.5241287 | -287555.6 |
| E(H2)= | -1.1785394 | -3094.3 |
| 3*E(H2)= | -3.5356181 | -9282.8 |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= | -0.0557907 | -146.5 |
Energy for converting hydrogen and nitrogen gas into ammonia gas:
ΔE=2*E(NH3)-[E(N2)]+3*E(H2)= -0.0557907 au = -146.5 kJ/mol.
As the reaction is exothermic, enegry is given out during the reaction to form NH3. Hence, NH3 gas is the more stable than the gaseous reactants.
Project molecule : SiH4 molecule
Summary information
| molecule name | SiH4 |
| Si-H bond distance | 1.485 |
| H-Si-H bond angle | 109.5 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D,P) |
| Final energy E(RB3LYP) in atomic units (au) | -291.8880276 a.u. |
| the point group | Td |
"Item" section in the log file
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
JMol of structure
Silane molecule |
File:YX8818 SIH4 OPTIMISATION.LOG
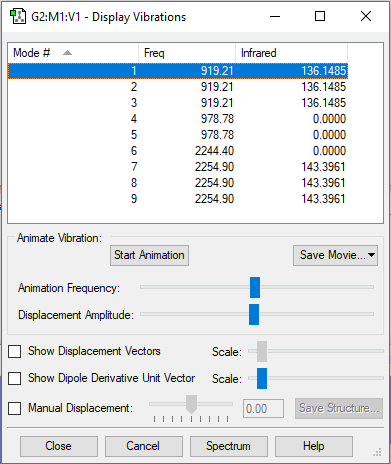
Snap shot of the display vibrations
Table of vibrations and intensities
| wavenumber cm-1 | 919 | 919 | 919 | 978 | 978 | 2244 | 2255 | 2255 | 2255 |
| symmetry | T2 | T2 | T2 | E | E | A1 | T2 | T2 | T2 |
| intensityin arbitrary units | 136 | 136 | 136 | 0 | 0 | 0 | 143 | 143 | 143 |
| image |  |
 |
 |
 |
 |
 |
 |
 |

|
| how many modes do you expect from the 3N-6 rule? | 9 |
| which modes are degenerate ? | The three vibrational modes at 919 cm -1 are degnerate.
The two vibrational modes at 978 cm-1 are degnerate. The three vibrational modes at 2255 cm -1 are degnerate. |
| which modes are "bending" vibrations and which are "bond stretch" vibrations? | The three modes at 919 cm -1 and the two modes at 978 cm-1 are bending.
The one mode at 2244 cm -1 and the three modes at 2255 cm-1 are bending. |
| how many bands would you expect to see in an experimental spectrum? | 2 bands are expected. |
NBO charges
| Si-atom | 0.629 |
| H-atoms | -0.157 |
Write a sentence saying what charge (positive or negative) you would expect for N and H and why
MOs of SiH4 molecule
MO1: HOMO
| Type of MO | Bonding MOs |
| Energy of MO in au | -0.35184 |
| What AOs contribute to the MO | 3p x AO of Si atom and the 1S, 2S AOs of H atoms. |
| Is the MO deep in energy, in the HOMO/LUMO region or high in energy? | In the HOMO/LUMO region |
| Is the MO occupied or unoccupied? | Occupied. |
| Which mode is highly symmetric? | Highly symmetric. |
MO2: LUMO
| Type of MO | Anti-bonding MOs |
| Energy of MO in au | -0.05053 |
| What AOs contribute to the MO | 3p x and 4p x AOs of Si atom and the 2S AOs of two H atoms. |
| Is the MO deep in energy, in the HOMO/LUMO region or high in energy? | In the HOMO/LUMO region |
| Is the MO occupied or unoccupied? | unoccupied. |
| Which mode is highly symmetric? | Highly symmetric. |
MO3
| Type of MO | Bonding MOs |
| Energy of MO in au | -0.54726 |
| What AOs contribute to the MO | 3s (58.2 %) and 4s (13.6 %) AOs of the Si atom and the 1s AOs on the four H2 atoms (13.0 % each). |
| Is the MO deep in energy, in the HOMO/LUMO region or high in energy? | high in energy |
| Is the MO occupied or unoccupied? | Occupied. |
| Which mode is highly symmetric? | Highly symmetric. |
MO4
| Type of MO | Non-bonding MOs |
| Energy of MO in au | -0.35184 |
| what AOs contribute to the MO | 2p x AO of Si atom. |
| Is the MO deep in energy, in the HOMO/LUMO region or high in energy? | Deep in energy. |
| Is the MO occupied or unoccupied? | Occupied. |
| Which mode is highly symmetric? | Highly symmetric. |
MO5
| Type of MO | Non-bonding MOs |
| Energy of MO in au | -0.35184 |
| What AOs contribute to the MO | 2s AO of Si atom |
| Is the MO deep in energy, in the HOMO/LUMO region or high in energy? | Deep in energy. |
| Is the MO occupied or unoccupied? | Occupied. |
Independence
All calculated molecular vibrations for NH3, N2,H2, and SiH4 are checked against literature values:
The values calculated are close to but not exactly equal to the literature values. This is probably because the calculations in Gaussian was undertaken in pure gaseous phase without the consideration of external envirnoment such as nearby electric and gravitational fields.
NH3
Table of experimental vibrations and intensities [1]
| wavenumber cm-1 | 3337 | 950 | 3444 | 1627 |
| symmetry | A1 | A1 | E | E |
| intensityin arbitrary units | 7.1 | 138.0 | 4.3 | 28.2 |
Table of calculated vibrations and intensities
| wavenumber cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| symmetry | A1 | E | E | A1 | E | E |
| intensityin arbitrary units | 145 | 14 | 14 | 1 | 0.3 | 0.3 |
N2
Table of experimental vibrations and intensities [2]
| wavenumber cm-1 | 2359 |
| symmetry | SGG |
| intensity in arbitrary units | - |
Table of calculated vibrations and intensities
| wavenumber cm-1 | 2457 |
| symmetry | SGG |
| intensity in arbitrary units | 0 |
H2
Table of experimental vibrations and intensities[3]
| wavenumber cm-1 | 4401 |
| symmetry | SGG |
| intensity in arbitrary units | - |
Table of calculated vibrations and intensities
| wavenumber cm-1 | 4466 |
| symmetry | SGG |
| intensity in arbitrary units | 0 |
SiH4
Table of experimental vibrations and intensities[4]
| wavenumber cm-1 | 2187 | 975 | 2191 | 914 |
| symmetry | A1 | E | T2 | T2 |
| intensityin arbitrary units | - | - | 282.0 | 381.0 |
Table of calculated vibrations and intensities
| wavenumber cm-1 | 919 | 919 | 919 | 978 | 978 | 2244 | 2255 | 2255 | 2255 |
| symmetry | T2 | T2 | T2 | E | E | A1 | T2 | T2 | T2 |
| intensityin arbitrary units | 136 | 136 | 136 | 0 | 0 | 0 | 143 | 143 | 143 |
References
- ↑ Koops, T., Visser, T. & Smit, W. M. A. Measurement and interpretation of the absolute infrared intensities of NH3 and ND3. J. Mol. Struct. 96, 203–218 (1983).
- ↑ C. GRAHAM D. A. IMRIE R. E. RAAB, C. G. D. A. I. R. E. Measurement of the electric quadrupole moments of CO 2 , CO, N 2 , Cl 2 and BF 3. Mol. Phys. 93, 49–56 (1998).
- ↑ Irikura, K. K. Experimental Vibrational Zero-Point Energies: Diatomic Molecules. J. Phys. Chem. Ref. Data 36, 389–397 (2007).
- ↑ Coats, A. M., McKean, D. C. & Steele, D. Infrared intensities of ν3 and ν4 in SiH4, GeH4 and SnH4. J. Mol. Struct. 320, 269–280 (1994).
Marking
Note: All grades and comments are provisional and subjecct to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, you could have explained that the charges are 0 as the electronegativities are equal.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
NO - but you included the unique identifier.
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4.5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
You have done a good job of presenting this information, well done! Probably this is a typo but you stated the modes at 2244cm-1 and 2255cm-1 to be bending vibrations. But these are stretching vibrations. You should have used an electronegativity argument to explain the atomic charges. Your MO analysis is very good!
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or
YES - well done! However, the given reason for differences in computed and real IR spectra is not the predominant one. The main difference should arise from the fact that gaussian uses the model of a harmonic oscillator. In reality molecules behave like an anharmonic oscillator.
Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
Overall you have done a really good job!