Rep:Mod:YW14115.TS
Transition States and Reactivity
Introduction
Along a reaction coordinate, transition state (TS) is the state has the highest energy. It is the least stable state compare to reactants and products. For a 2 dimensional energy diagram, TS is on the local maxima. As a stationary point, it has zero gradient with negative second derivatives (maximum negative curvature). Reactant and product are the minimum points with zero gradient and positive minimum curvatures. Investigating the TS is important to confirm the mechanism of a reaction. In reality, there are more than one degree of freedom for a chemical system and real potential energy surface has 3N-6 dimension. The each one of 3N-6 degree of freedom corresponding to a normal mode which has different force constant and hence vibration. A 3-D PES is plotted with energy against every degree of freedom and varying two reaction coordinates. In 3-D PES, TS is on the saddle point which is local maxima from one direaction but also local minima from other directions. The TS in on the point has only negative curvature along the reaction coordinate.
Nf710 (talk) 21:21, 10 January 2018 (UTC) Nice intro but you need to be carefull when explaining your 2D case. A diagram would have explained it better
Method
Huge calculation are needed to find out the TS, computational calculations are required. In this experiment, the TS of three different pericyclic reactions are located with Guassian. The optimisation process is introduced briefly here. When carrying out optimisation, the position of the nuclei is chosen first by building molecules in Gaussian. The Schrodinger equation is then solved for the fixed nuclear positions (Born-Oppenheimer approximation) , and obtain an energy E and wavefunction Φ which are dependent on the frozen position of the nuclei. This process is called self consistent field (SCF). The energy change with the nuclear position. SCF helps you to find electronic wavefunction which gives the lowest energy by moving the nuclear position a small amount. This is also called single point calculation which is used in this experiment. As mentioned earlier, at equilibrium (zero forces) the first derivative of PES (along reaction coordinate) is zero. That is the structure we are looking for. This is how computer performs an optimisation. The semi-empirical method PM6 and Density Functional Theory (DFT) method B3LYP with basis set 6-31G are used for optimisation. The method decides the particular type of hamiltonian employed and the basis-set determine the number of functions used to descirbe the electronic structure. In this experiment, possible geometries of transition states are generated with PM6 then further optimized with B3LYP. By doing frequency calculation in Gaussian to check vibration mode, the correct transition state can be confirmed. As we are calculating the frequency of harmonic oscillator with a negative force constant due to stretching of bond breaking/forming, 'negative' frequency for the first normal mode of the transition state would be expected. In principle, a TS should contain only one imaginary (negative) frequency. If there are more than one imaginary frequency, that is due to higher order saddle point. On the other hand, no imaginary frequency should be observed for reactants and products. However, one imaginary frequency at TS is still not sufficient. Further Intrinsic reaction coordinate (IRC) calculation is required to confirm the TS.
Nf710 (talk) 21:21, 10 January 2018 (UTC) Nice understanding. Some equations would have have made it clearer. and some understanding of the quantum methods would have been nice.
Exercise 1: Reaction of Butadiene with Ethylene
This is a typical [4+2] cycloaddition which is also called Diels-Alder reaction. Diels-Alder reaction involves a conjugated alkene and a dienophile. The Diels–Alder reaction is useful in synthetic organic chemistry as a reliable method for forming 6-membered systems with good control over regio- and stereochemical properties. It is essential to study the TS to get a better understanding of the reaction. In this reaction, 1,3-butadiene (conjugated alkene) is reacting with ethylene (dienophile) to form cyclohexene (reaction scheme shown above).
Optimization method and results
The structure of reactants and products are optimized to minimum at PM6 level. The optimized reactants structure are further used to generate TS. As this is a bond forming reaction, distance 2.20 Å is used for formation of C-C bond at TS. This value is between their combined Van der Waals radii and a C-C bond length. A guessed TS is build first in Gaussian then optimized by PM6 method. Optimisation results for product, reactants and TS are shown below.
| Butadiene | Ethlyene | Transition State | Cyclohexene | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
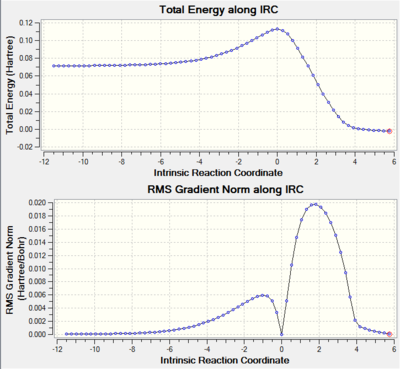
The transition state is located and confirmed with a frequency calculation and IRC. Results are shown below.
 |
 |
There is only one imaginary frequency observed for vibration mode which confirm the TS is correct. Further IRC calculation confirms the desired TS. Along the reaction coordinate, reactant, product (minima) and TS (maxima) all have zero gradient.
Molecular Orbital (MO) Analysis
| Butadiene | Ethylene | Transition state | Transition state | |
|---|---|---|---|---|
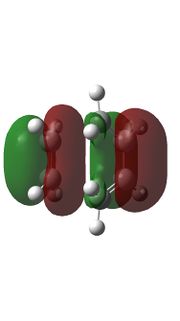
| HOMO |  |
 |
 |
 |
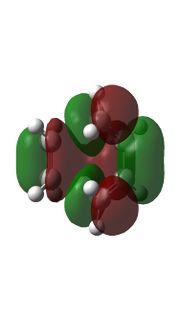
| LUMO |  |
 |
 |
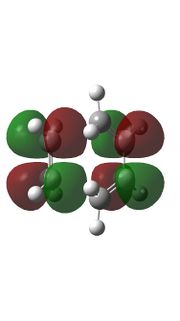 |
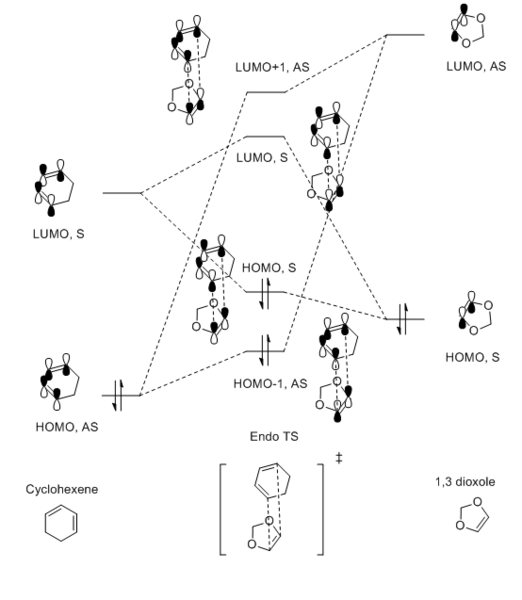
Relavent MO, LUMO and HOMO are shown above for reactants, TS and products which can help to understand how MO of reactants are combined to form TS and what symmetry these MOs have.
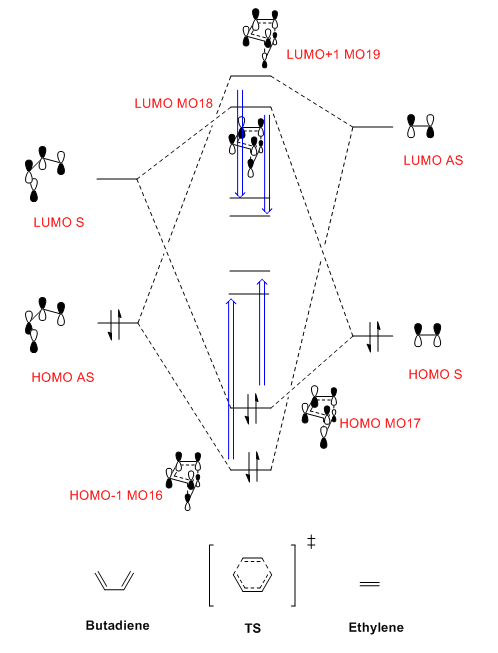
(Fv611 (talk) Good MO, but I would be wary of showing the product MOs and the TS ones on the same diagram without an appropriate caption. Additionallym you forgot to add symmetry labels to your TS MOs, and included the wrong picture for your ethylene LUMO.)
By observing the MO of reactants, TS and products, a MO diagram can be constructed shown above. The symmetry lables 'S' and 'AS' corresponding to symmetric and anti-symmetric respectively. Anti-symmetrical has a C2 rotational axis and symmetrical has a sigma mirror plane with respect to the sigma bond lies in the middle of MO. The AS HOMO of butadiene is interacting with the AS LUMO of ethylene and S LUMO of butadiene is interacting with the S HOMO of ethylene to form new MO. One thing can be concluded from the MO is that only orbitals of the same symmetry can interact. MOs with the same symmetry combine with each other to give a TS MO with the same symmetry. This is because interaction between same symmetry MOs can give a non-zero overlap intergral and interaction between different symmetry can give a zero overlap intergral. For a reaction to happen, there must be some extent of orbitals overlap. A table of relationship between overlap intergral and symmetry of interaction is shown below.
S - AS interaction ---------> Zero S - S interaction ---------> Non-zero AS - AS interaction ---------> Non-zero
The energy gap between LUMO and HOMO is smaller for butadiene because it is more electron-rich than ethylene
According to calculation, the energy of HOMO and HOMO-1 are higher than expected and LUMO and LUMO+1 are lower than expected. This is because the electrons of the chemical system are very delocalised at TS. There are mixing between the HOMO and the LUMO in some extent. As a result, the HOMO is raised up and the LUMO is going down.
Bond Length Analysis
The bond lengths of reactants, products and TS are shown in the above table. Typical sp3 and sp2 C-C bond lengths are shown below:
sp2-sp2 C=C bond length 1.34 Å sp3-sp3 C-C bond length 1.54 Å sp2-sp2 C-C bond length 1.47 Å sp2-sp3 C-C bond length 1.50 Å
The C-C and C=C bond lengths of butadiene and ethylene are same as the typical valuse. During the reaction, the ethylene C=C bond length increase from 1.33 Å to 1.38 Å at TS. This is because the C=C bonds are partly breaking to form a C-C bond. The C=C bonds of butadiene lengthened from 1.33 Å to 1.38 Å at TS and the C-C bond shorten from 1.47 Å to 1.41 Å at TS. The distance between reacting terminal carbons between reactant at TS is 2.11 Å. The Van der Waals radius of the C atom is 1.7 Å so the distance between to carbon atoms is 3.4 Å which is larger than 2.11 Å. This is because the bonds are partly formed, there is significant attraction between them. The bond lengths are then further decrease to 1.54 Å which is same as sp3-sp3 C-C bond length. From that, we can conclude the new bonds are formed in the product. The rest of bond lengths of product are typical compare to typical value. To maintain these favourable bond lengths, the product adopts a twisted structure.
(Fv611 (talk) Good, but could have added the comparison of the length of the bond being formed in the TS with the length of a single C-C bond as further proof that the bond is on the way to being formed.)
Vibrational Analysis
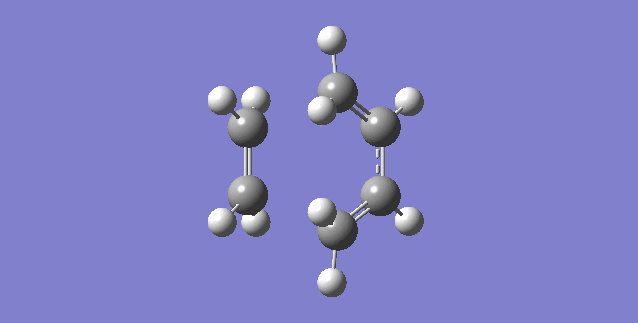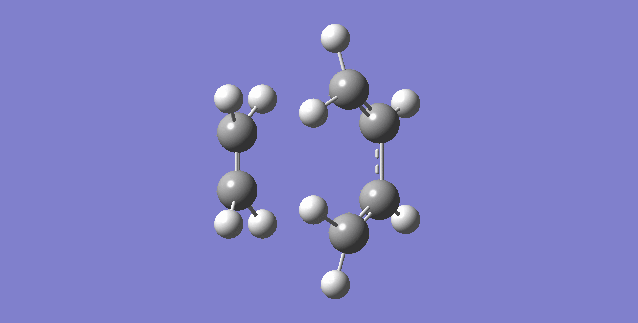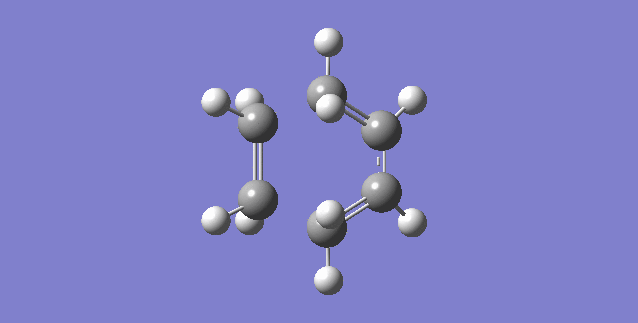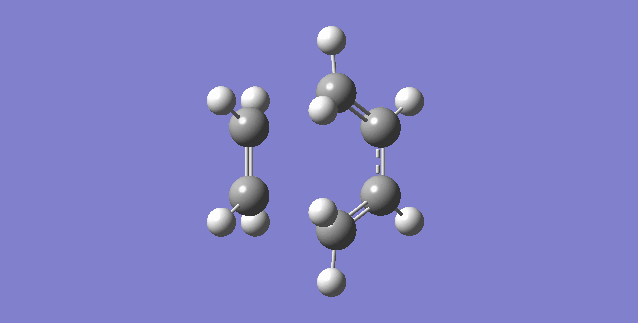
The first vibration animation is shown above. The formation of the two bonds at TS is synchronous. The two terminal carbon atoms of ethylene and two terminal carbons of butadiene approaching to each other at the same time.
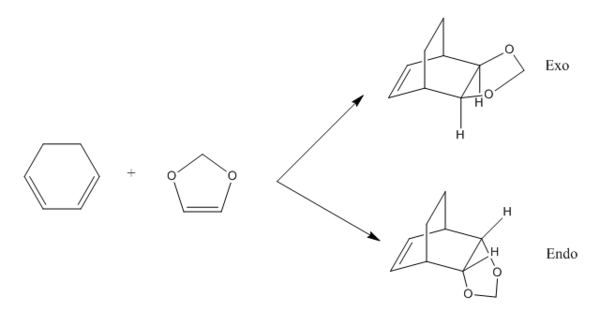
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
This is another Diels-Alder reaction between cyclohexadiene and 1,3-dioxole. The reaction can undergo either exo or endo pathway to form different products. The difference in reaction energy and activation barrier between the two are investigated.
Method and Optimization Results
The structure of reactants and products are optimized to minimum at PM6. The optimized reactants structure are further used to generate TS by positioning with different geometries. These structure are then further optimised at B3LYP/6-31G. The optimised results are shown below:
By doing frequency calculation, reactant, TS and products are confirmed to be correctly optimized. Only one imaginary frequency is found for each case.
MO analysis
| EXO TS MO | 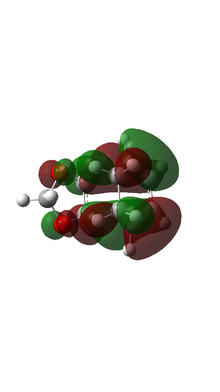 |
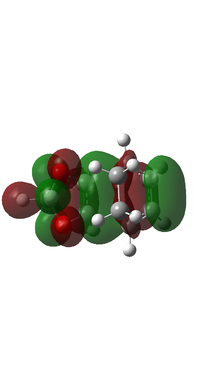 |
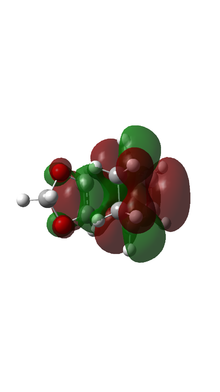 |
 |
| ENDO TS MO | 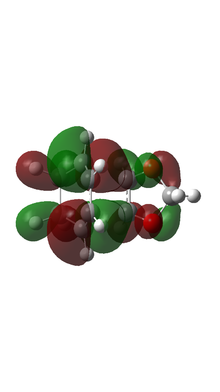 |
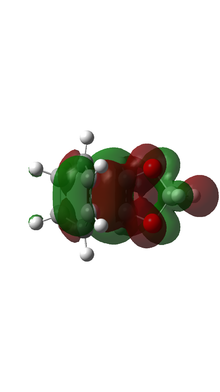 |
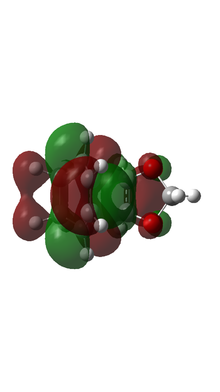 |
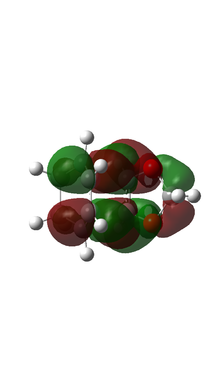 |
|

|
Based on MO calulation for the TS, MOs from reactants are paired up accordingly. This particular Diels-Alder reaction reaction involves a cyclohexadiene(conjugated diene) and a 1,3-dioxole (dienophile). Reactivity is controlled by relative energies of frontier molecular orbitals. The key interaction is between the HOMO of one reactant and LUMO of the other. The closer the energy of the two interacting orbitals the faster the reaction rate. Consequently, two types of Diels-Alder reaction are often occurred which are normal demand Diels-Alder reaction and inverse demand Diels-Alder reaction. For normal demand DA reaction, the HOMO of a electron rich diene overlap with the LUMO of electron poor dienophile. For inverse demand DA reaction, the LUMO of electron poor diene overlap with the HOMO of electron rich dienophile. According to the MO calculation followed by the construction of MO diagrams, both exo and endo reactions are inverse demand DA reaction. This is proved quantitatively by doing a single point energy calculation at the combined reactant geometries and reactants. The LUMO energy of cyclohexadiene is lower than the LUMO energy of 1,3 dioxole. The HOMO energy of cyclohexadiene is lower than the HOMO energy of 1,3 dioxle. This is because the presence of two oxygen atoms in 1,3-dioxole. Their lone pairs are donate to the C=C bond. Consequently, the energy of HOMO and LUMO of 1,3-dioxole are higher. The resultant energy gap between LUMO of cyclohexadiene and HOMO of 1,3 dioxole has a value 0.21404 a.u. which is smaller than the energy gap between HOMO of cyclohexadiene and LUMO of 1,3-dioxole 0.24263 a.u. The inverse electron demand is the overall outcome.
(Fv611 (talk) Good discussion, and well done on putting both Endo and Exo diagrams. However, the latter loses it's purpose if you do not modify the MO energies accordingly: you have put them to be the same for both cases, when in reality they are different.)
Reaction barrier and reaction energy
| Substrates | Gibbs free energy at B3LYP (6-31G(d)) / kJmol-1 |
| Cyclohexadiene | -612625 |
| 1,3-Dioxole | -701204 |
| Sum of reactant energy | -1313829 |
| Exo-TS | -1313662 |
| Exo-Product | -1313891 |
| Endo-TS | -1313669 |
| Endo-Product | -1313894 |
| B3LYP (6-31G(d)) / kJmol-1 | ||
|---|---|---|
| Exo | Endo | |
| Activation barrier (Eact) /kJmol-1 | + 167.69 | + 159.98 |
| Reaction energy /kJmol-1 | - 61.23 | - 64.77 |
The activation barrier is calculated by taking the energy difference of TS and sum of reactants. The reaction energy is calculated by taking the energy difference of product and sum of reactants. From the table shown above, the endo reaction has a smaller activation energy than exo reaction. Therefore, endo reaction is kinetically favoured. In addition, the endo reaction has a more negative reaction energy. Endo product is also thermodynamically more favourable.
|
|
|---|
Endo TS is lower in energy compare to exo Ts due to secondary orbital interaction (SOI). In the case of endo TS, the non-bonding p orbitals of oxygen atoms in 1,3-dioxole interacting with LUMO of cyclohexdiene (pi conjugation) through space. This interaction stabilise the TS and lowers the activation barrier which makes endo product more kinetically favourable. SOI doesn't explain the more negative reaction energy as the pi conjugation of cyclohexadiene doesn't appear in the product. The reason is actually due to steric clashes. The exo reaction is more sterically hindered due to the sp3 bridge head carbon which makes it less thermodinamically favoured.
Nf710 (talk) 21:30, 10 January 2018 (UTC) Good section. your emergies are slightly out but your conclusions are correct. If you did run the orbital quantitatively to shown inverse demand it would have been nice to see this. a diagram of sterics + SSO would have been nice.
Exercise 3: Diels-Alder vs Cheletropic
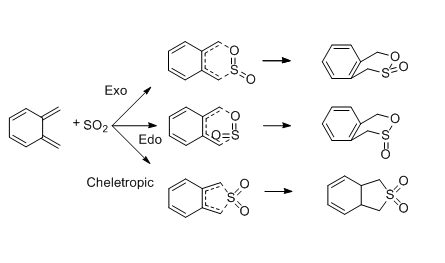
This is an example of a hetero-Diels Alder reaction between xylyene and sulfur dioxide, where sulfur dioxide is used as a dienophile. The reaction can undergo Diels-Alder type or Cheletropic type. There are also two Diels-Alder paths(endo and exo) exist for Diels-Alder reaction. which route is preferred is investigated.
Optimisation results
| Optimisation of TS of EXO | Optimisation of TS of Endo | Optimisation of TS of cheletropic | ||||||
(The frames you've chosen for the jmols are inconsistent and probably refer to other systems. The transition vector (imaginary frequency) frame for the first structure, for example, is 15 Tam10 (talk) 11:53, 3 January 2018 (UTC))
IRC Analysis
| Approach trajectory of endo product formation | Endo product formation IRC |
|
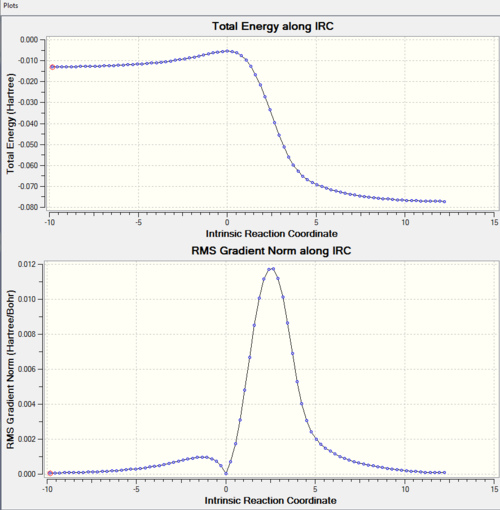
|
| Approach trajectory of exo product formation | Exo product formation IRC |
|
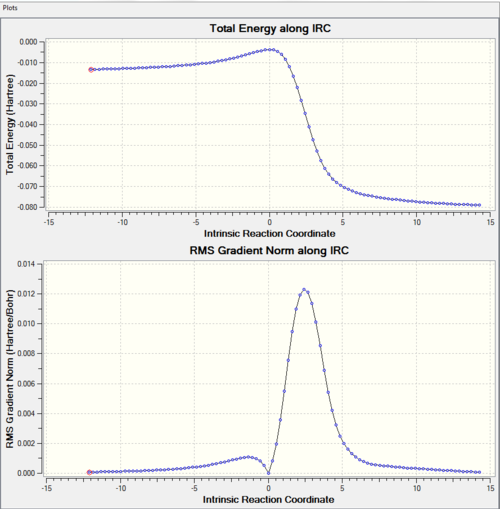
|
| Approach trajectory of cheletropic product formation | Cheletropic product IRC |
|
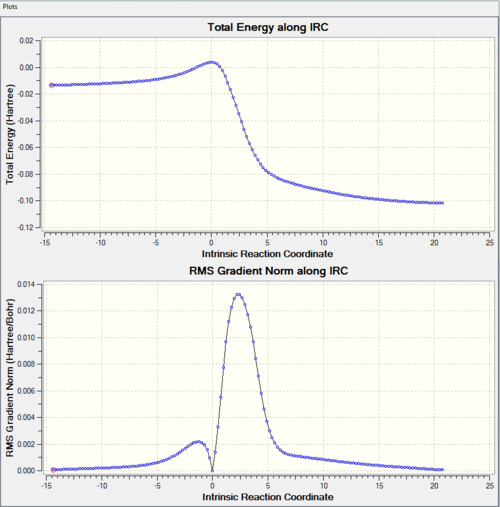
|
From the IRC, we can see that the activation barrier is small (compare to reaction in exercise 1). This is because xylylene is highly unstable and Diels-Alder reaction is favourable. This can be explained by following reasons. Xylyene can either have 4 π electrons in the ring, or 6 π electrons and a diradical. The latter one is highly unstable. The first one behaves antiaromatic which is also not very stable. However, the product is aromatic which makes cycloaddition very favourable energetically. In addition, xylyene has a rigid structure. The geometry cis-diene (not in the ring) is locked down in position which makes Diels-Alder reaction highly favourable. The orbitals of diene can overlap with the orbital of dienophile easily. This is proved by the approaching trajectory shown above. There is little rearrangement for the xylyene as the cis diene is already in the correct geometry. During the course of the reaction, the bond lengths of the 6-membered ring of xylyene is changed. Xylylene has C=C bond length 1.35 Å and C-C bond length which are 1.46 Å, 1.47 Å and 1.49 Å. All three pathways form the same product with same C-C bond length 1.47 Å of the 6-membered ring. This is between C-C bond (1.54 Å) and C=C bond (1.34 Å). This is due to the delolocalistion of π electrons. This change can be visiualise by IRC. From that we can the C=C bonds of six-membered ring are stretching and the C-C bonds are shortening.
(Good analysis and justification for the energetics Tam10 (talk) 11:53, 3 January 2018 (UTC))
Reaction barrier and reaction energy
| Substrates | Gibbs free energy at B3LYP (6-31G(d)) / kJmol-1 |
| SO2 | -311.421 |
| Xylyene | 467.649 |
| Sum of reactants energy | 156.228 |
| Exo-DA-TS | 241.751 |
| Endo-DA-TS | 237.770 |
| Exo-Cheletropic-TS | 260.087 |
| Exo-DA-product | 56.325 |
| Endo-DA-product | 56.968 |
| Cheletropic product | -0.0131 |
| PM6 / kJmol-1 | |||
|---|---|---|---|
| Exo DA | Endo DA | Cheletropic | |
| Activation energy /kJmol-1 | + 85.52 | + 81.54 | + 103.86 |
| Reaction energy /kJmol-1 | - 99.90 | - 99.26 | - 256.22 |
(You've subtracted an additional 100 kJ/mol from the cheletropic reaction energy Tam10 (talk) 11:53, 3 January 2018 (UTC))
Reaction Profile
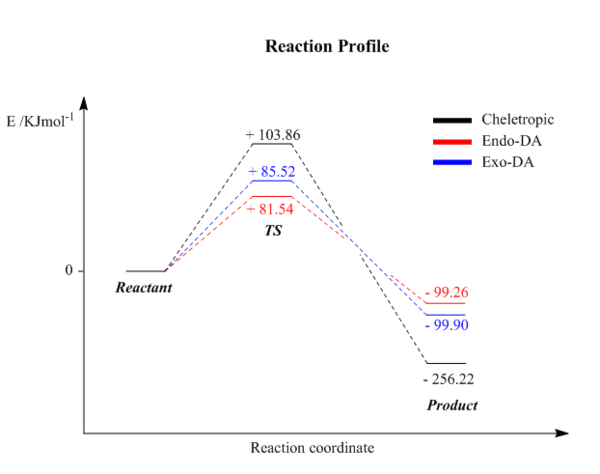
A reaction profile is shown on the left. The reactants are set to zero energy at infinite separation. Endo DA reaction requires least amount of activation energy which makes this pathway more kinetically favourable. Cheletropic reaction has the most negative reaction energy which means this pathway is more thermodinamically favourable. The difference between exo DA reaction and endo DA reaction is small in terms of activation barrier and reaction energy. This is because the SOI is not significant in TS and little steric effect of products. On the other hand, Cheletropic product is very stable compare to DA product. This is due to the presence of large sulfur atom within the five-membered ring which relief the ring strain.
(Again, a good analysis Tam10 (talk) 11:53, 3 January 2018 (UTC))
Conclusion
Gaussian can optimise structures to minimum and allow us to find the TS. Frequency calculation and IRC allow us to confirm if the TS is correct by looking for presence of one imaginary frequency and looking at the gradients along the reaction coordinate respectively. By doing MO analysis, we can conclude that only MOs with the smae symmetry can overlap and produce non-zero overlap intergral. Combines MOs have the same symmetry as the fragment MOs. MO analysis also provide us information with matching of fragment MOs from reactants. By doing single point energy calculation for MO, the energy gap between interacting LUMO and HOMO can be easily determined. From that, we can tell whether the specific Diels-Alder reaction is normal electron demand or inverse electron demand. By doing energy calculation for activation barrier and reaction energy, we can tell which reaction pathway (if there is more than one) would be more favourable under thermodynamic condition and kinetic condition. In general, computational method uses computer simulation which is more efficient to assist in solving chemical problems. It provides information which can not be observed by tradition experimental method. To obtain a better result, basis set 6-311G(d,p) can be used which can perform calculation at higher level with better accuracy.
LOG File
Exercise 1.
| Substrates | Method |
|---|---|
| PM6 | |
| Butadiene | File:YWU EX1 BUTADIENE.LOG |
| Ethene | File:YWU EX1 ETHYLENE.LOG |
| TS | File:YWU EX1 TS.LOG |
| Cyclohexene | File:YWU EX1 PRODUCT.LOG |
| IRC | File:Ywu ex1 IRC.LOG |
Exercise 2.
| Substrates | Method |
|---|---|
| B3LYP/6-31G | |
| Cyclohexadiene | File:Ywuex2CYCLO 631G.LOG |
| 1,3-dioxole | File:Ywuex2Ox 631g.LOG |
| TS of EXO | File:Ywuex2EXO TS 631G.LOG |
| TS of Endo | File:Ywuex2ENDO TS 631G.LOG |
| Exo product | File:Ywuex2EXO PRODUCT 631G.LOG |
| Endo product | File:Ywuex2ENDO PRODUCT 631G.LOG |
Exercise 3.
| Species | Method | IRC |
|---|---|---|
| PM6 | ||
| TS of EXO | File:Ywu ex3 TS PM6.LOG | File:Ywu ex3 exo ts IRC PHASE.LOG |
| TS of Endo | File:Ywu ex3 DAendoPM6.LOG | File:Ywu ex3 endo IRC PHASE.LOG |
| TS of cheletropic | File:Ywu ex3 CHE TS PM6.LOG | File:Ywu ex3 chele IRC WITH PHASE.LOG |