Rep:Mod:YURU1
BH3 Molecule
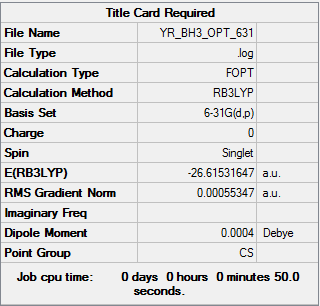
Optimization of BH3
Optimization method used: RB3LYP
Basis set used: 6-31G (d.p)
Figure 1 The summary table of optimasation
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000018 0.001200 YES
Table 1 the item table
Frequency analysis of BH3
• Link to frequency LOG file
Low frequencies --- -2.9884 -1.1079 -0.0054 1.6554 9.9523 10.0137 Low frequencies --- 1162.9840 1213.1744 1213.1770
Table 2 the frequency table
Borane molecule |
Figure 2 Jmol image BH3 Molecule
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
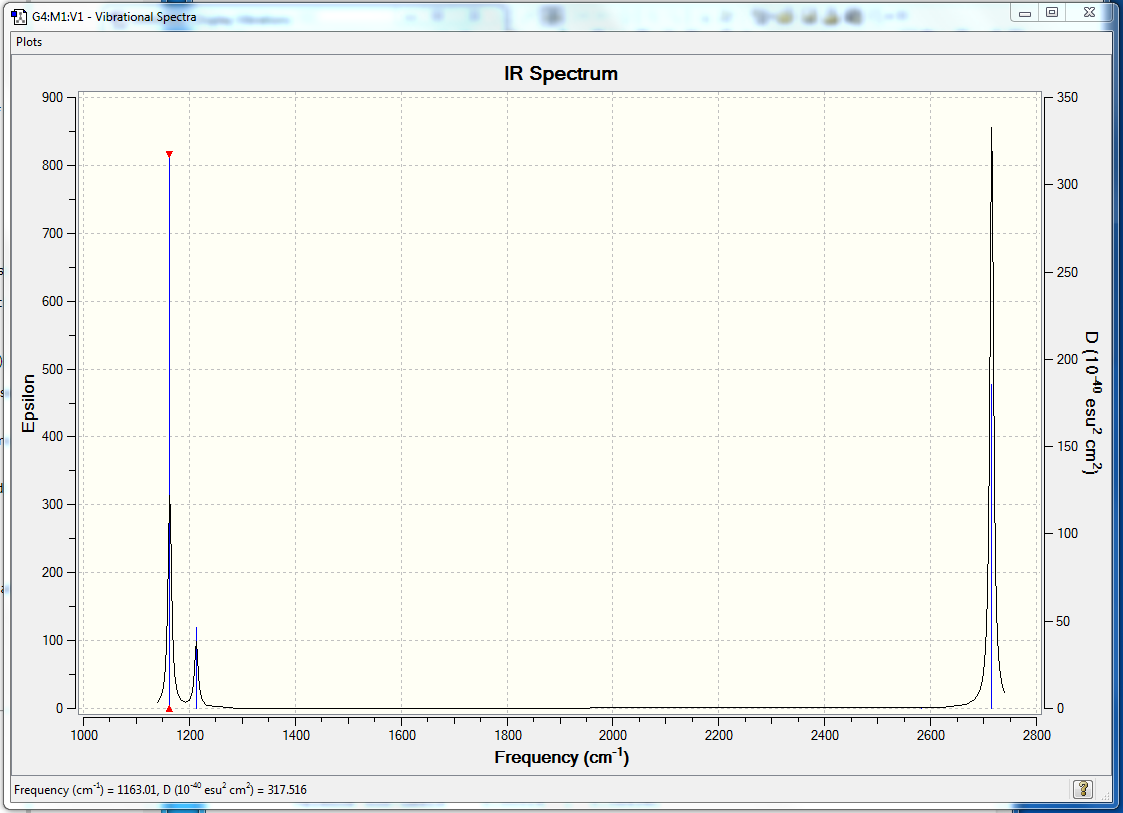
| 1163 | 93 | A1 | yes | out-of-plane bend |
| 1213 | 14 | E | very slight | bend |
| 1213 | 14 | E | very slight | bend |
| 2582 | 0 | A1 | no | symmetric stretch |
| 2715 | 126 | E | yes | asymmetric stretch |
| 2715 | 126 | E | yes | asymmetric stretch |
Table 3 Vibrational analysis
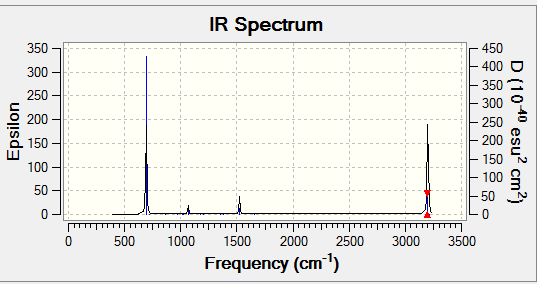
Figure 3 The expected IR spectrum of BH3
• Explanation to the vibration modes and the IR spectrum
There six vibration modes in total which agrees with the 3N-6 rule. However, only three signals can be found on the expected spectrum. The symmetric stretch mode is not IR active due to the fact that it does not result a change in the dipole moment. The two bending modes are energetically degenerate and the two asymmetric stretches are energetically degenerate causing the overlapping of the signals, resulting in only 3 signals could be found in the IR spectrum.
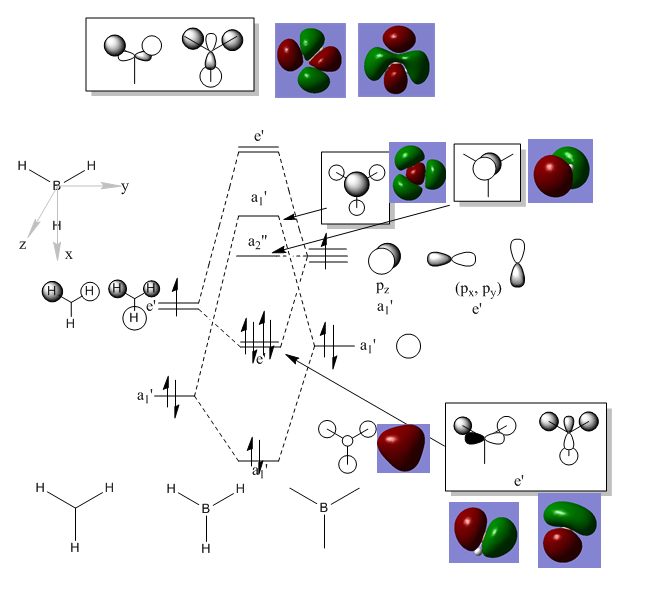
Visualising molecular orbitals of BH3
•There is no significant difference between MO theory and MO. How ever more interaction needs to be taked into consider when computing MO. Ng611 (talk) 23:48, 15 May 2018 (BST) 'more interaction' is a little vague. What exactly do you mean. You're correct for saying that there are minimal significant differences though.
• MO is extremely accurate and useful for finding structures and estimate energies of molecules.
Figure 4 the MO diagram and MO visualisation of BH3
Association energy
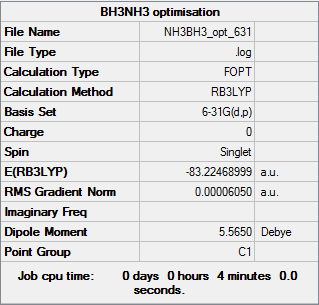
We first need to optimize BH3NH3.
Figure 5 summary table of NH3NH3 optimisation
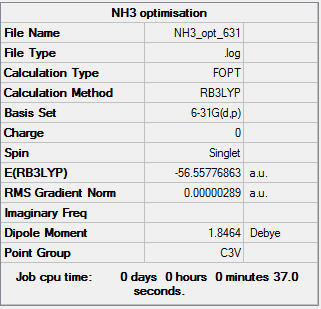
We then need to optimize NH3.
Figure 6 summary table of NH3 optimisation
By the principle of Hess's Law: Calculation of dissociation energy:
E(NH3)=-56.55776863 a.u. E(BH3)=-26.61531647 a.u. E(NH3BH3)=--83.22468999 a.u. ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] =-83.22468999+56.55776863+26.61531647 =-0.05160489 a.u. =-135 KJ/mol
BBr3 Molecule
BBr3 Molecule optimisation
Optimization method used: RB3LYP
Basis set used: GEN
Figure 7 summary table of BBr3 optimisation
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Table 4 the item table for BBr3 optimisation
Frequency analysis of BBr3
Low frequencies --- -0.1016 -0.0466 -0.0053 108.8524 109.2834 109.2835 Low frequencies --- 1166.7548 1215.7105 1215.7131
Table 5 the frequency table for BBr3 frequency analysis
Link to log file: Media:YR_BBr3_FREQ.log
Dspace Link:
Project: Aromaticity
Optimization method used: RB3LYP
Basis set used: 6-31G (d.p)
Benzene molecule
Figure 8 Summary table of benzene
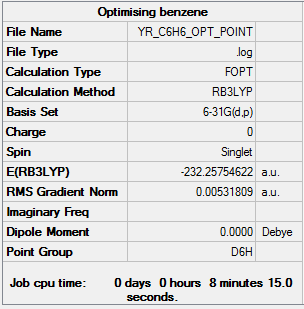
Benzene optimization
Item Value Threshold Converged? Maximum Force 0.000199 0.000450 YES RMS Force 0.000081 0.000300 YES Maximum Displacement 0.000847 0.001800 YES RMS Displacement 0.000299 0.001200 YES
Table 5 the item table for benzene
Benzene frequency analysis
Link to the log file: Media:YR_C6H6_FREQ.LOG
Low frequencies --- -4.6046 -4.6046 -0.0088 -0.0042 -0.0041 9.6590 Low frequencies --- 413.9386 413.9386 621.1428
Table 6 low frequencies of benzene
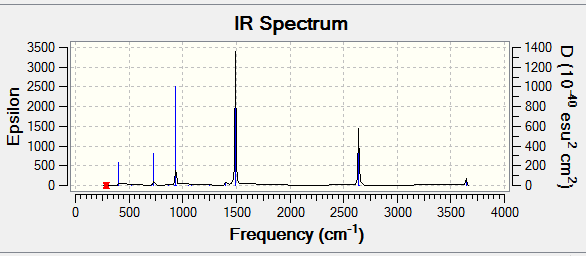
Figure 9 Expected IR of benzene
• No negative frequeny found
Benzene molecule |
Figure 10 Jmol of benzene
Benzene molecule
Figure 11 Summary table of borazine
Borazine optimization
Item Value Threshold Converged? Maximum Force 0.000085 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000251 0.001800 YES RMS Displacement 0.000075 0.001200 YES
Table 7 the item table for borazine
Borazine frequency analysis
Link to log file:Media:YR_B3N3_FREQ.LOG
Low frequencies --- -6.8010 -6.4836 -6.4658 -0.0101 -0.0050 0.1536 Low frequencies --- 289.1988 289.2075 403.7534
Table 8 low frequencies of borazine
Figure 12 Expected IR of borazine
• No negative frequeny found
Borazine molecule |
Figure 13 Jmol of benzene
Charge analysis and intepretation
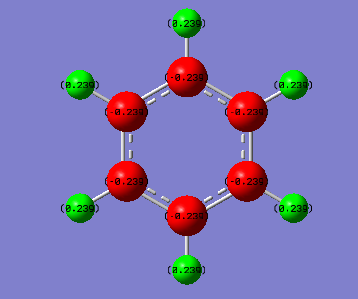
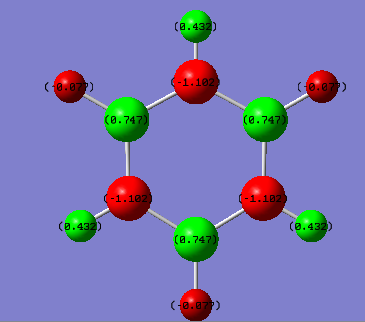
figure 14 (a) charge distribution of benzene (left) (b) charge distribution of borazine (right)
| element (cm-1 | charge (e) | electronegativity |
| C | -0.239 | 2.5 |
| H | +0.239 | 2.1 |
| element (cm-1 | charge (e) | electronegativity |
| N | -1.102 | 2.5 |
| H-B | -0.077 | 2.1 |
| H-N | 0.432 | 2.1 |
| B | 0.747 | 2.0 |
figure 9 (a) charge distribution of benzene (top) (b) charge distribution of borazine (bottom)
Discussion: For benzene molecule. All the C atoms are carrying the same charge and are δ-. All H atoms carries the same charge and are δ+ due to it is less electonegative compared to C.The charges are evenly distributed in the molecule resulting no net dipole-moment. This is due to the high symmetry of the molecule, which has D6h point group. This shows that the molecule has a C6 rotation axis and therefore all the 6 C are equivalent and all 6 H are equivalent.
However, the borazine molecule is less symmetric compared to benzene and has only a D3h symmetry with a C3 rotation axis. There 3 H of the 6 H are equivalent, and the rest 3H are equivalent to each other. H connected to electronegative N becomes δ+ and the H connected to electropositive B becomes δ+.
Ng611 (talk) 23:50, 15 May 2018 (BST) Excellent discussion! Remember to use identical colour scales though for ease of visual comparison.
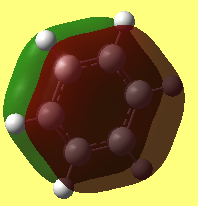
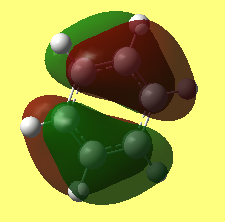
MO comparison of benzene and borazine
| MO Benzene | MO Borazine | Description |
|
|
These are the anti bonding orbitals resulting from original px orbitals |
|
|
These orbitals are the pi bonding molecular orbitals. However their symmetries are different. Benzene ring is symmetric with C6 axis while borazine has contractions around electronegative N. |
|
|
MO 21 is the anti-bonding pi orbital. Resuting from pz orbitals with different symmetry for the two molecules |
Ng611 (talk) 23:51, 15 May 2018 (BST) A reasonable MO analysis. I would add more rationalisation regarding differences between benzene and borazene's MO's
MO and aromaticity
Aromaticity describes a phenomenon that a planar cyclic molecule which satisfies Huckle's law are highly symmtric and extremely stable. Convensional ways view it as a struture with delocalisation of pi electrons. The resonance forms gives extreme stability. From MO point of view, it can be seen view as the the overlaping of orbitals, ie. Pz orbitals. As shown in the benzene and borazene MO above, many mixing of energy similar artomic orbitals of the same symmetry are found in aromatic compounds and this leads to the stabilization of the molecule.
The LCAO suggest that overlapping Pz gives the aromatic properties. However, this ignore many other orbital interaction resulting a inaccurate calculation to the the energy.
Ng611 (talk) 23:54, 15 May 2018 (BST) What you've written is true but it is a basic understanding that has largely been supplanted by more modern descriptions of aromaticity incorporating QM. A discussion of these modern models of aromaticity would have aided this discussion further, as would some additional discussion about experimental findings..
Ng611 (talk) 23:54, 15 May 2018 (BST) Adequate but missing a few bits. You generally didn't include the requisite data with your calculations, especially for NH3/BH3NH3 in Section1. Otherwise section 1 was good. Charge analysis was good but remember to use the same colour scale for both molecules. You also need to comment on the partial charges adding to 0 -- even if this is obvious to you, mention it. More detail in your MO discussion (WHY are the differences in orbital shapes) and your aromaticity discussion would have strengthened this section further.