Rep:Mod:YUDAOQINPHY

Optimizing the Reactants and Products

Introduction

In this lab, computational methods (software such as Gaussian)will be used to compare the different energies for several reactions or compound. HF/3-21G and HF/6-31G(D) level of theory are adopted most. Activation energies, enthaplpies and many other data are in remarkably agreement with real experiment values.^[1]

In this part, GaussView will be firstly used to build the structures of 1-5 hexadiene conformers and then optimized them at the level of HF/3-21G. After that, a series of results such as point group, vibrational frequency, energy of structure gain. Comparison with the experiment values and the calculated ones lead to an better visualisation.

1,5-hexadiene optimisation
Name	gauche1	gauche3	gauche5	anti3	anti2	anti-2
Image of Structures
Calculation type	FOPT	FOPT	FOPT	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF	RHF	RHF	RB3LYP
Basis set	3-21G	3-21G	3-21G	3-21G	3-21G	6-31G(d)
Point group	C2	C1	C1	C_2h	C_i	C_i
Energy/a.u.	-231.68771610	-231.69266122	-231.68961575	-231.68907066	-231.69253528	-234.61170280
.log File	GAUCHE1	GAUCHE3	GAUCHE5	ANTI_3	ANTI2	ANTI2_6-31G

A few of conformers were found and relative data such as point group and energy were listed above. Each of them owns different energies to distinguish their stability, the lower the energy the more stable the conformer is. For example, gauche3 shows the highest stability since it has the lowest energy (-231.69266122 a.u. which matches the reference exactly, -231.69266 a.u. while considering five decimal places given in the appendix 1^[1]). Furthermore, two alkenes in gauche3 conformer stay farthest with each other while compare with the gauche conformers, hence less steric interactions it experiences. It is worth mentioning that anti2 displays a relatively low energy as well since the four central carbons adopted antiperiplanar conformation, two terminal double bonds stay far away from each other to minimize the interactions (the picture above demonstrates the property clearly). In contrast, four central carbons in gauche1 and gauche5 does not show the antiperiplanr structure, thus they experience higher and leads to lower stability. Last but not the least, compare the structures from the HF/3-21G optimization with B3LYP/6-31G(d) optimization, overall geometry remains (C_i). Also, dihedral angles in both cases are almost the same.

Energies on the bare potential energy surface have been shown above. However, frequency calculation is a must while in comparison with the experimental data.

Anti-2 frequency data
Image of Structure
Calculation type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Point Group	C_i
Energy/ a.u.	-234.61170280
Sum of electronic and zero-point energies ((E = E_elec + ZPE))	-234.469212
Sum of electronic and thermal energies (E = E + E_vib + E_rot + E_trans)	-234.461856
Sum of electronic and thermal enthalpies (H = E + RT)	-234.460912
Sum of electronic and thermal free energies (G = H - TS)	-234.500821
.log File	anti2 6-31G

An infrared spectrum proves that energies calculated at HF/6-31G(d) level of theory are relatively higher than that calculated using HF/3-21G level of theory which matches the appendix2^{[1]^.}

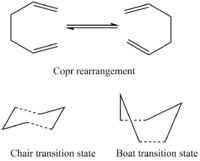
Optimizing the "Chair" and "Boat" Transition Structures

At first, allyl did the optimization at HF/3-21G level of theory. After that, it looked like half of the transition state. Then recombined two allyls to form a chair or boat transition state structure. They are given below. It is worth mentioning that the distance between two terminal carbons are 2.02Å.

Hessian, frozen coordinate and QST2 method

In this case, a few of methods (Hessian, frozen coordinate, QST2) were adopted to optimize chair and boat transition structures(images are shown in previous part). The aim of these types of calculations was to find out the activation energies during the Cope rearrangement.

Chair and boat transition state optimization
Method	Hessian	Frozen coordinate	Frozen coordinate (further)	QST2
Structure	chair	chair	chair	boat
Calculation type	FREQ	FREQ	FREQ	FREQ
Calculation method	RHF	RHF	RHF	RHF
Basis set	3-21G	3-21G	3-21G	3-21G
Point group	C_2h	C_2h	C_2h	C_2v
Energy/a.u.	-231.61932238	-231.61932238	-231.61932237	-231.60280200
Transition bond distances/ Å	2.02	2.02	2.02	2.14
.log file	optimized guess chair	optimized transition state	optimized transition state further	1-5 hexadiene angle change

Hessian method gives the result of imaginary frequency = 818 cm^-1 corresponds to the Cope rearrangement of 1,5-hexadiene exactly since the deviation of structure can be virtually neglected while compare with the true one. Comparing the Hessian and the frozen coordinate methods, both of them give the same bond lengths of 2.02 Å due to the symmetrical structure of the transition state. However, the precision of Hessian methods decreases dramatically while the symmetry breaks (huge deviation of curvature). Then frozen coordinate method will be a more ideal choice. On the other hand, the animation in QST2 shows an imaginary frequency of magnitude 840 cm-1 corresponds to the Cop rearrangement transformation.

Intrinsic reaction coordinate method

In this case, the connection of the anti and gauche conformation need to be considered yet it is quite hard to proceed. IRC with forward direction (symmetrical structure) and 50 intermediates was proceeded, followed by HF/3-21G normal minimization (fastest, but cannot check the accuracy of the energy minimized structure)^[1] to gain the result below. Maximized number of intermediates and find out the intermediate which contains the minimum energy will be the most precise pathway. Nevertheless, it is quite time consuming while there are thousands, even millions of intermediates...

Intrinsic reaction coordinate method
Structure	chair
Calculation type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Point Group	C2
Energy/ a.u.	-231.69166702
.log File	IRC optimized transition state

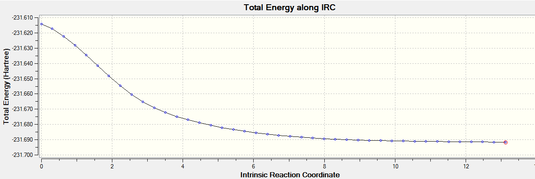
Activation energy calculation

In order to gain the activation energies of chair and boat transition state, reoptimized both of them at HF/6-31G(d) level of theory as well as frequency calculations after HF/3-21G, made the difference and converted into right units. As a result, geometries are similar, but the energy difference are huge.

Reoptimization the transition state of chair and boat
Method	Hessian (chair)	Frozen coordinate (chair)	QST2 (boat)
Structure	chair	chair	boat
Calculation type	FREQ	FREQ	FREQ
Calculation method	RB3LYP	RB3LYP	RB3LYP
Basis set	6-31G(D)	6-31G(D)	6-31G(D)
Point group	C_2h	C_2h	C_2v
Energy/a.u.	-234.55698303	-234.55698299	-234.54309306
.log file	chair hessian 6-31G	chair frozen coordinate 6-31G	boat qst 6-31G

Summary of energies(in hartree)

HF/3-21G
Energy	Electronic Energy (a.u.)	Sum of Electronic and Zero-point Energies at 0K (a.u.)	Sum of Electronic and Thermal Energies at 298K (a.u.)	.log File
Chair T.S.	-231.61932238	-231.466700	-231.461340	chair T.S.
Boat T.S.	-231.60280200	-231.450928	-231.445299	boat T.S.
Reactant (anti2)	-231.69253528	-231.539539	-231.532565	anti2

HF/6-31G(d)
Energy	Electronic Energy (a.u.)	Sum of Electronic and Zero-point Energies at 0K (a.u.)	Sum of Electronic and Thermal Energies at 298K (a.u.)	.log File
Chair T.S.	-234.55698303	-234.414929	-234.409009	chair T.S.
Boat T.S.	-234.54309306	-234.402342	-234.396007	boat T.S.
Reactant (anti2)	-234.61170280	-234.469212	-234.461856	anti2

Although there are two different forms of chair transition state since two distinct methods (Hessian and Frozen coordinate method) are used, the energy difference between them are less than 0.0001%. Hence, only one of them is given.

Summary of activation energies (in kcal/mol)
	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G(d)	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.69	44.69	34.05	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.97	41.32	44.7 ± 2.0

1 hartree = 627.509 kcal/mol

The real activation energy of the chair and boat transition state were given to be 33.5±0.5 kcal/mol and 44.7±0.2 kcal/mol experimentally at 0K respectively^[1], it proves that reoptimazation at B3LYP/6-31G(d) level of theory gives a quite reasonalble values.

The Diels Alder Cycloaddition

AM1 semi-empirical molecular orbital method was carried out in all following steps.

Cis butadiene

Cis-butadiene was optimized by the AM1 method and the HOMO and LuMO of its structuere were both visualized. The properties of them are listed below.

Cis butadiene summary
Structure	HOMO	LUMO
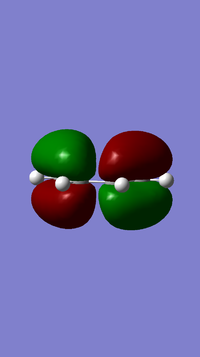	anti-symmetric with the plane	symmetric with the plane


Calculation type	Calculation method	Basis set	Point group	Energy/a.u.	.log File
FREQ	RAM1	ZDO	C_2v	0.04879719	cis butadiene

Ethylene + cis butadiene transition structure

Prototype reaction:

A guess of the partly formed C-C bond length becomes an essential. 2.2Å and 2.5Å of the partly formed C-C bond gave out a successful optimization.

Ethylene + cis butadiene transition structure
Structure
HOMO	Anti-symmetric with the plane
LUMO	Symmetric with the plane
Calculation type	FREQ
Calculation Method	RAM1
Basis Set	ZDO
Point Group	C_s
Energy/ a.u.	0.11165470
.log File	guessing transition state

Typical sp³ and sp² C-C bond lengths are 1.54Å and 1.47Å.^[2] The van der Waals radius of the C atom is 1.70Å.^[3] The partly formed σ C-C bonds (dashed lines) which shown below are 2.12Å. The relative long and weak bond lengths of 2.12Å points out the bond is not completely formed during the reaction. Imaginary vibrational frequency of magnitude 956 cm^-1 (below left) correspondes to the Diels Alder cycloaddition formation. Likewise, the real lowest frequency of 147 cm^-1 (below right) stands for the opposite direction of vibration. It is independent with the bond formation yet the vibration of molecule itself. This animation proves that formation of the two bonds (dashed lines) in both cases are synchronous.

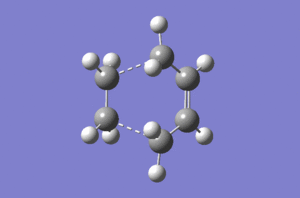
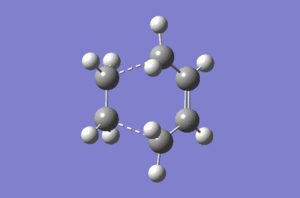
Imaginary vibrational frequency = 956cm^-1 (dashed line = partly formed σ C-C bonds)

Vibrational frequency = 147cm^-1 (dashed line = partly formed σ C-C bonds)

On the other hand, both of the HOMO structure of cis butadiene and the LUMO structure of ethylene show anti-symmetry. Therefore, the new bonds (MO formation) are contributed by them since they have the same symmetry and lead to an increase the density of bond overlap.

Regioselectivity of the Diels Alder reaction

A guess of the partly formed C-C bond length is an essential. 2.5Å for both of the partly formed C-C bond gave out a successful optimization.

Cyclohexa-1,3-diene reaction with maleic anhydride
	Exo transition state	Endo transition state
Structure
HOMO
LUMO
Calculation type	FREQ	FREQ
Calculation Method	RAM1	RAM1
Basis Set	ZDO	ZDO
Point Group	C_S	C_S
Energy/ a.u.	-0.05041983	-0.0515047
.log File	Exo	Endo

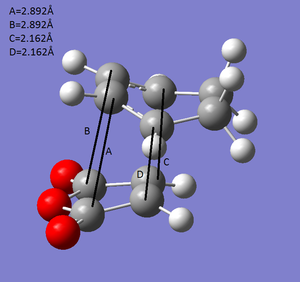
Endo transition state forms while the maleic anhydride attacks from top to the cyclohexa-1,3-diene, exo transition state forms while maleic anhydride attacks from back to the cyclohexa-1,3-diene. Endo has relatively low energy due to the secondary orbital overlap. In endo structure, pi orbitals of two carbon atoms in the double bond have a extra overlap with the upper layer (A and B in endo structure), which forms secondary orbital overlap to stabilize overall structure. In contrast, four specific four carbons in exo structure stay too far away to form extra overlap. On the other hand, -(C=O)-O-(C=O)- fragment in endo stays far away from the two top carbons to minimize the steric strain in comparison with exo structure.

References

1: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3

2: Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer. ISBN 978-3-86025-249-9

3: a b c Bondi, A. (1964). "Van der Waals Volumes and Radii". J. Phys. Chem. 68 (3): 441–51. doi:10.1021/j100785a001.