Rep:Mod:YTL14

Introduction

A potential energy surface (PES) is used to analyse the molecular structure change in a chemical reaction. In a simple diatomic molecule, the 1D PES is a curve resulting from the combination of functions considering (1) the repulsion between the two atoms at very short internuclear distance (2) Coulombic attraction between the two ions and (3) energy at equilibrium is represented by a Harmonic oscillator. This provide a curve with energy at the y-axis and internuclear distance or the reaction coordinate at the x-axis. This estimation is good for simple diatomic molecule formation/dissociation.

However, as the molecule becomes larger more variables are involved. The degrees of freedom (3N-6 for non-linear structure, while 3N-5 for linear molecule; N is the number of atom) gives the dimensionality of the PES. In the determination of degrees of freedom, the translational and rotational energy of the molecule are opt out as the potential energy of a molecule does not change upon translation or rotation in space. PES is dependent on the relative position of the one atom to another (geometry).

A minima on PES is a point corresponds to either transition states, reactants, products and intermediates. It can be classified as local minima or global minima. A saddle point on a PES is the maximum connecting two minima in the minimum energy pathway, i.e the transition state. As at this point going down either direction will result in a lower energy conformation/structure. The gradient and thus the force at the transition state is zero. The same applies to the minima. These points at which the forces are zero also known as stationary point. A frequency calculation of the stationary point allows one to understand the nature of the structure at that particular point such as frequency, vibrational modes etc. The transition state is the first saddle point by definition and is indicated by the presence of one negative frequency (imaginary frequency).

Nf710 (talk) 17:46, 21 March 2017 (UTC) I can see that you have a very good understanding here, however you should have explained this with second derivatives.

Exercise 1: Reaction of Butadiene with Ethylene

Method 2 was used. The reactants, transition state and product are optimised at PM6 level.

Diels-Alder reaction is thermal cycloaddition between a conjugated, electron-rich diene and an electron-poor dienophile. The conjugated diene must adopt a s-cis conformation. The interaction between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of the reactants participate in bond formation. As electron density 'flows' (or charge transfer) from HOMO to LUMO.

Figure 1: Plane of symmetry

Table 1: HOMO and LUMO of butadiene and ethene

Species	HOMO	LUMO
Butadiene
Ethene

Table 2: MOs of transition state

Species	MO
Transition state	Interaction between HOMO of ethene and LUMO of butadiene
	HOMO, Bonding	LUMO, Antibonding
	Interaction between LUMO of ethene and HOMO of butadiene
	HOMO-1, Bonding	LUMO+1, Antibonding

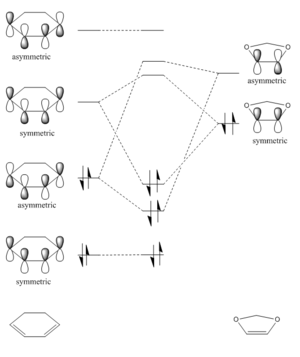
From the transition state MOs, it is clearly shown that the interacting MOs are as follow:

1. HOMO (butadiene) - LUMO (ethene) give HOMO-1 and LUMO+1. All four MOs are asymmetric. 2. LUMO (butadiene) - HOMO (ethene) give HOMO and LUMO. All four MOs are symmetric.

Hence it is confirmed that for an allowed interaction, the HOMO and LUMO have to be of the same symmetry. While for the case where the interacting MOs are of different symmetry the reaction is forbidden.

Figure 2: MO diagram of the reaction.

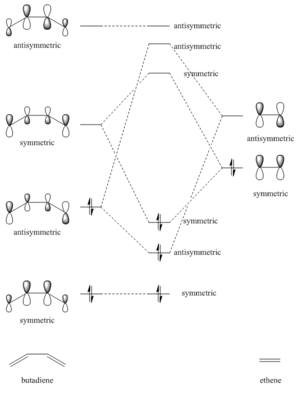
The two bonding MOs generate the two new C-C σ-bonds in 1-cyclohexene.

Figure 3: Symmetry requirements

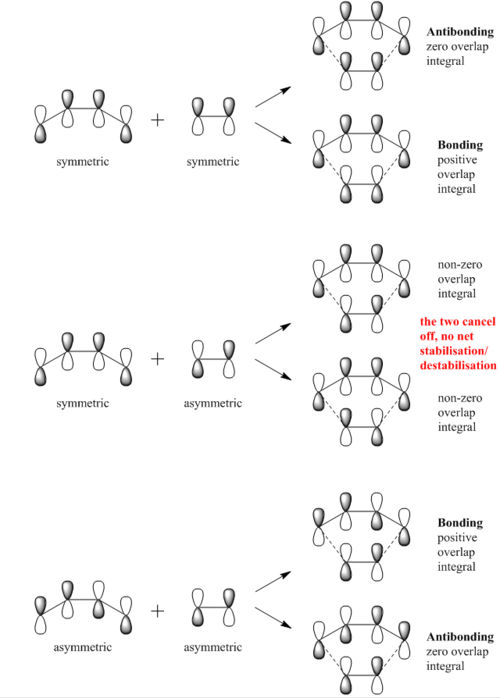
(Fv611 (talk) 17:31, 15 March 2017 (UTC) While your MO diagram in Figure 2 is correct, there is a lot of confusion on the transition state MOs in Figure 3. I think you are forgetting that we are talking about orbital overlap, not electron density overlap. Both bonding and antibonding interactions will yield a non-zero orbital overlap if they arise from fragment orbitals with the same symmetry (S/S or AS/AS). On the other hand, S/AS interactions are not allowed because they result in a zero orbital overlap. Additionally, you wrongly assigned antibonding and bonding to the MOs arising from S/S combinations in Figure 3 (the top transition state MO is the bonding orbital). Finally, the correct term is antisymmetric, not symmetric.)

Table 3

Reactants	Product	Vibrations at transition state
Carbon labelled in reactants	Carbon labelled in product

Figure 4:Internuclear Distance plotted against the Reaction Coordinate for Dissociation of 1-cyclohexene

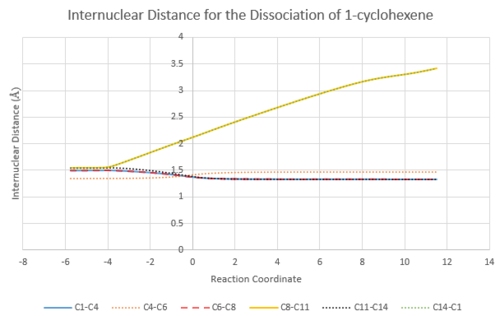
IRC showed the dissociation of 1-cyclohexene to butadiene and ethene. Referring to Figure 4, reaction coordinates at -5.73, 0 and 11.49 correspond to product, transition state and reactants respectively.

Two sp3 C-C bonds are formed between C8 and C11, and C14 and C1. New sp2 C=C bond is formed between C4 and C6. The sp2 C=C and sp3 C-C bond lengths are of good comparison to literature (1.36 Å and 1.54 Å respectively). The Van der Waals radius of a carbon atom is 1.70 Å. In the transition state, the distance between the carbons forming new bonds are 2.115 Å, which is in between two times the Van der Waals radius (3.40 Å) and 1.70 Å.

Table 4: Changes in bond length during the course of the reaction

Bond broken
Reactant	Bond length (Å)	Transition state	Bond length (Å)	Product	Bond length (Å)
C11=C14	1.327	C11--C14	1.382	C11-C14	1.541
C1=C4	1.335	C1--C4	1.38	C1-C4	1.501
C6=C8	1.335	C6--C8	1.38	C6-C8	1.501
Bond formed
Reactant	Bond length (Å)	Transition state	Bond length (Å)	Product	Bond length (Å)
C4-C6	1.468	C4--C6	1.411	C4=C6	1.338
C8,C11	non-bonding	C8--C11	2.115	C8-C11	1.54
C14,C1	non-bonding	C14--C1	2.115	C14-C1	1.54

TS bond lengths resemble the reactants' bond length (compare to products'), hence according to Hammond's postulate this is an early transition state. Formation of the two bonds is synchronous, i.e concerted, with the same bond lengths. No radical nor ionic intermediates was formed.

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

In this exercise, Diels-Alder reaction of cyclohexadiene and 1,3-Dioxole were studied. The reactants, transition states and products were optimised at PM6 level. The transition states were reoptimised at B3LYP-6d to confirm the structure obtained. Thermochemistry study was performed using the IRC data obtained at PM6 level.

Table 5: HOMO and LUMO of Cyclohexadiene and 1,3-Dioxole

Species	HOMO	LUMO
Cyclohexadiene	Asymmetric	Symmetric
1,3-Dioxole	Symmetric	Asymmetric

The HOMO of cyclohexadiene and LUMO of 1,3-dioxole are both asymmetric, hence they interact to form LUMO+1 and HOMO-1 orbitals in the transition states. Meanwhile, the LUMO of cyclohexadiene and HOMO of 1,3-dioxole are both symmetric. The interaction of both results in HOMO and LUMO orbitals in the transition states.

Table 6: MOs of the transition state in endo and exo pathway

Endo pathway		Exo pathway
LUMO+1, Asymmetric	LUMO, Symmetric	LUMO+1, Asymmetric	LUMO, Symmetric
HOMO, Symmetric	HOMO-1, Asymmetric	HOMO, Symmetric	HOMO-1, Asymmetric

(Use antisymmetric. Asymmetric means a lack of symmetry and antisymmetric means the sign/phase is changed when the symmetry operation is performed Tam10 (talk) 16:31, 15 March 2017 (UTC))

Figure 5: Energy profile of the reactions

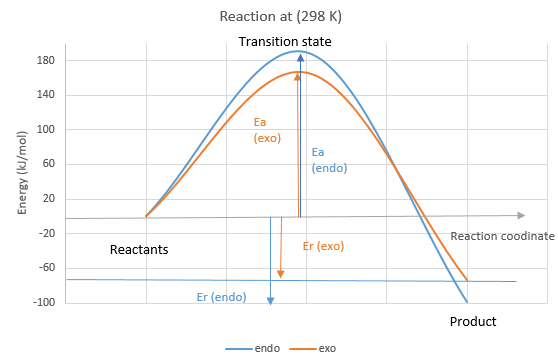
(Avoid placing different IRCs on the same coordinate. Energies of stationary points such as reactants, TS and products can be compared this way, but the x axis of an IRC is specific Tam10 (talk) 16:31, 15 March 2017 (UTC))

The endo product is both the thermodynamic (more negative reaction energies (Er), indicative of a higher stability) and kinetic product (lower activation energy (Ea), hence the endo product forms faster). Hence endo product is the major product.

Nf710 (talk) 18:05, 21 March 2017 (UTC) Thats is not what your graph is showing?

Diels-Alder reaction between cyclohexadiene and 1,3-Dioxole are inverse electron demand. The 1,3-dioxole is electron rich due to the delocalisation of oxygen lone pair into the pi-system of 1,3-dioxole. This creates a repulsion of the donated electron and HOMO electrons. This results in a rise in HOMO energy, which then has a comparable energy with the LUMO of the diene. The LUMO of 1,3-dioxole and HOMO of cyclohexadiene are closer in energy. Hence they interact more strongly than HOMO of 1,3-dioxole and LUMO of cyclohexadiene.(HOMO-diene and LUMO-dienophile interact stronger in normal oxygen demand Diels-Alder).

Figure 6: Inverse electron demand of Diels Alder

Table 7: Thermochemistry data

Energy	0 K		298 K
	Endo	Exo	Endo	Exo
Reactant (Hartree/particle)	0.120615	0.118665	0.065793	0.075809
Transition state (Hartree/particle)	0.172488	0.173266	0.137941	0.138906
Product (Hartree/particle)	0.070675	0.070929	0.037802	0.037976
Activation energy (kJ/mol)	136.1926	143.3549	189.4351	165.6612
Reaction energy (kJ/mol)	-131.117	-125.3309	-99.33054	-73.4799

In Diels-Alder reaction, the endo pathway is normally the preferred pathway due to secondary interaction which is said to lower the energy of the transition state.

Figure 7: Secondary interaction between carbon and oxygen

Oxygen is marked red.

Nf710 (talk) 18:10, 21 March 2017 (UTC) You have done your calculations at PM6 and therefore got the wrong answers. You should have used B3LYP You have also contradicted yourself with the graph.

Exercise 3: Hetero-Diels-Alder and Cheletropic of o-xylylene and SO₂

The Hetero-Diels-Alder and Cheletropic reaction between o-xylylene and SO₂ were studied. The products of these reactions were firstly optimised, the newly formed bonds on the optimised product were broken and followed by optimization of the distorted structure. IRC calculation was performed on the transition states obtained. The reactants and products from the IRC were re-optimized. All calculations were done at PM6 level.

Table 8 Thermochemistry data

Energy	0 K			298 K
	Endo	Exo	Cheletropic	Endo	Exo	Cheletropic
Reactant (Hartree/particle)	0.116934	0.116955	0.114807	0.058769	0.059656	0.070991
Transition state (Hartree/particle)	0.126589	0.128172	0.13556	0.090559	0.092082	0.099062
Product (Hartree/particle)	0.057503	0.056644	0.034556	0.021704	0.021455	0.0000002
Activation energy (kJ/mol)	25.34395	29.45023	52.43245	83.45939	85.13446	70.92138
Reaction energy (kJ/mol)	-156.0413	-158.3465	-70.92138	-97.31941	-100.2967	-179.3638

Figure 7: Energy profile of cheletropic and Diels Alder reactions

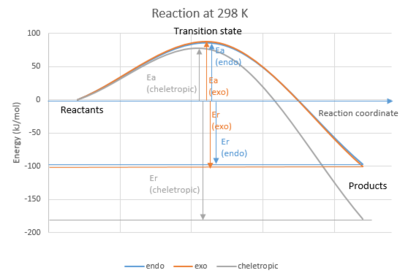
(We asked that you used the sum of the energies of xylylene and SO2 for consistency Tam10 (talk) 16:31, 15 March 2017 (UTC))

From Table 8 and Figure 7, it was found that cheletropic product was the thermodynamic and kinetic product.

Table 9: Endo, exo and cheletropic reaction compared

Reaction	Transition state	Product	IRC
Diels Alder (Endo)
Diels Alder (Exo)
Cheletropic

Diels-Alder and cheletropic products all contain an aromatic benzyl group. At the beginning of the reaction, the six-membered ring in xylylene has 2 C=C bonds. As the new bonds begin to form, all the six bonds are in conjugation (C-C bond is in between C-C single bond and C=C bond). The products formed are aromatic with pi-orbital above and below the plane. Xylylene is unstable compared to the product. Aromaticity is the driving force of the reaction.

(Fairly short write-up for this section Tam10 (talk) 16:31, 15 March 2017 (UTC))