Rep:Mod:YQ816
NH3 molecule
Optimisation
The Jmol image of the ammonia molecule |
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -56.55776873 a.u.
RMS Gradient Norm = 0.00000485 a.u.
Point Group = C3V
N-H bond distance = 1.01798 Å
H-N-H bond angle = 105.741 Å
The "Item" table:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986283D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is liked to QIANYIKAI_NH3_OPTF_POP.LOG
Vibrations
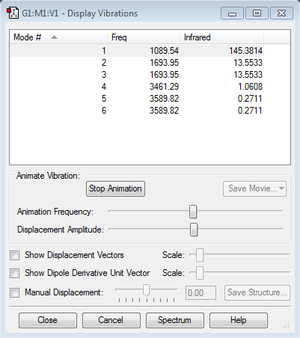
The ammonia molecule has 4 atoms and is linear. Therefore there expected to be 6 modes of vibration from the 3N-6 rule. Among the 6 modes, there are 2 pairs of degenerate modes (i.e. they have the same energy). As a result, there are only 4 bands are observable from the IR spectrum. The vibrations with frequencies of 3461.29Hz and 3589.82Hz are "stretching" vibrations. The left vibrations are "bending" vibrations. Mode 1 and Mode 4 is highly symmetric, between which Mode 1 is the so-called "umbrella" mode.
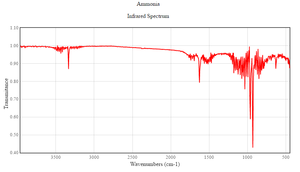
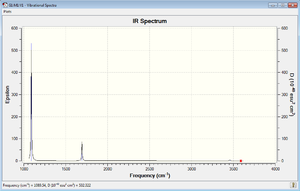
In both practical and expected there shows 3 obvious at around 1000cm-1, 1700cm-1 and 3400cm-1.However, the Mode 5 and 6 vibration is highly unrecognisable due to its low intensity. This is because these vibration modes give very little dipole moment.
Compared to the expected spectrum, the real spectrum has many noises due to the background light and the fingerprint on the sample. The peak value between the practical and the expected spectrum is not exactly the same due to the influence of the surroundings of the practical sample.
Charges
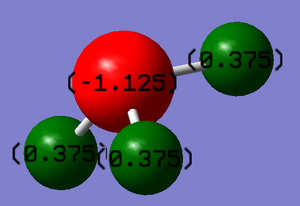
The nitrogen atom is expected to have a negative charge whilst the hydrogen atom should be positive because the nitrogen atom is more electronegative than the hydrogen atom.
N2 molecule
Optimisation
Molecule: N2
The Jmol image of the nitrogen molecule |
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -109.52412868 a.u.
RMS Gradient Norm = 0.00000060 a.u.
Point Group = D*H
N-N bond distance = 1.10550 Å
The "Item" table:
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400996D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is liked to QIANYIKAI_N2_OPTF_POP.LOG
Vibrations
The nitrogen molecule has 2 atoms and is non-linear. Therefore there expected to be 1 modes of vibration from the 3N-5 rule. However, the vibration is completely symmetric, so there is no dipole during the vibration. Therefore, the spectrometer cannot detect the intensity.
Charges
Nitrogen is a diatomic molecule. Therefore the charges on the two atoms should be identical.
H2 molecule
Optimisation
Molecule: The Jmol image of the hydrogen molecule
NH |
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -1.17853936 a.u.
RMS Gradient Norm = 0.00000017 a.u.
Point Group = D*H
H-H bond distance = 0.74279 Å
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is liked to QIANYIKAI_H2_OPTF_POP.LOG
Vibrations
The hydrogen molecule has 2 atoms and is non-linear. Therefore there expected to be 1 modes of vibration from the 3N-5 rule. Similar to the nitrogen molecule, the intensity of the IR spectrum is zero.
Charges
Hydrogen is a diatomic molecule. Therefore the charges on the two atoms should be identical.
The energy of the Haber-Bosch process
The energy of the ammonia molecule E(NH3) = -56.55776873 a.u.
so, 2E(NH3) = -113.11553746 a.u.
The energy of the ammonia molecule E(N2) = -109.52412868 a.u.
The energy of the ammonia molecule E(H2) = -1.17853936 a.u.
so, 3E(NH3) = -3.53561808 a.u.
The reaction formula of the Haber-Bosch process is: N2 + 3H2 -> 2NH3
Therefore, the enthalpy change ΔE=2*E(NH3)-[E(N2)+3*E(H2)] = -0.0557907 a.u. = -146.47848285 kJmol-1
The literature value of the Haber-Bosh process is -92 kJmol-1. [2]
The calculation method of the GaussianView determines the lowest energy of the molecule. However, in the real life, the molecules possess different energies. Therefore the literature value and the calculated value is very different.
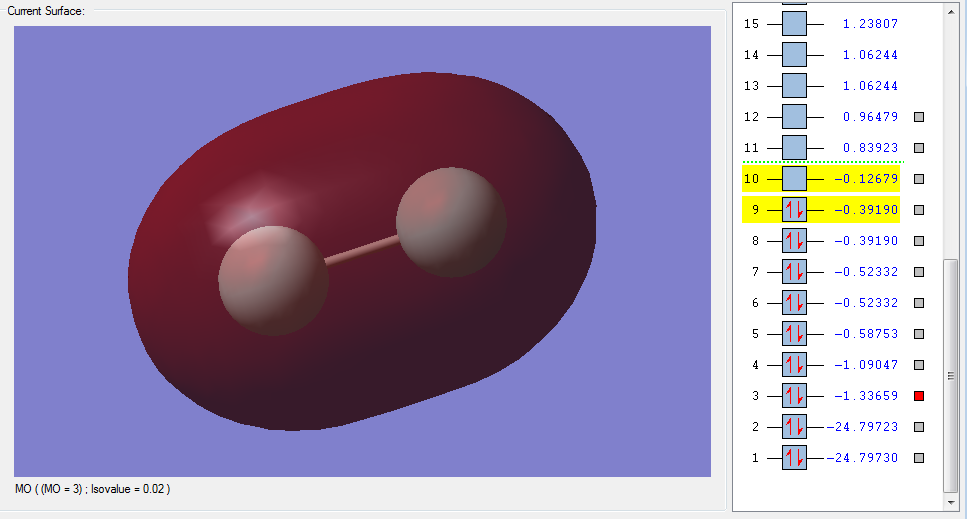
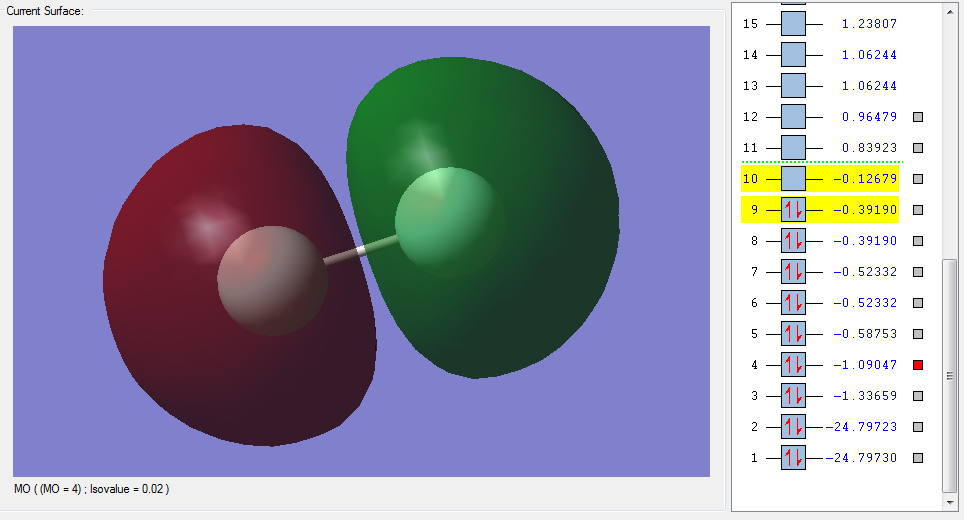
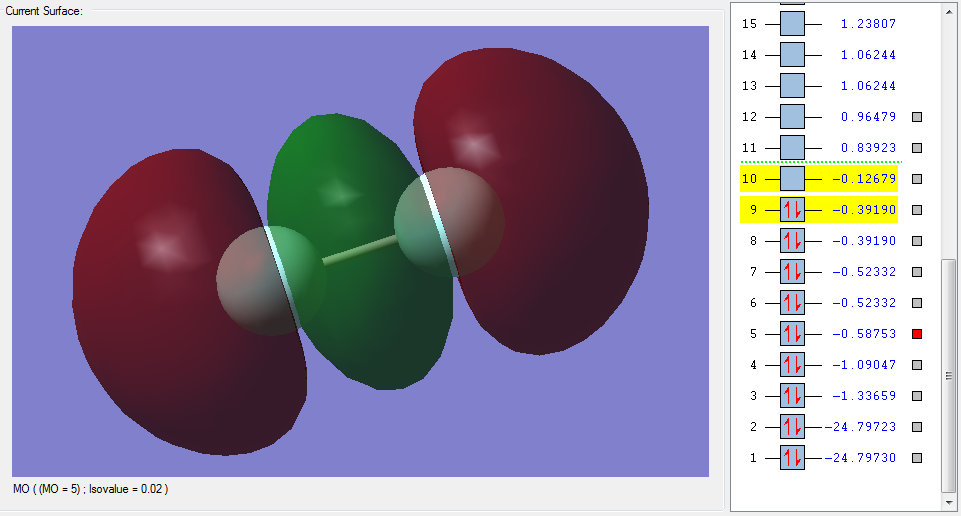
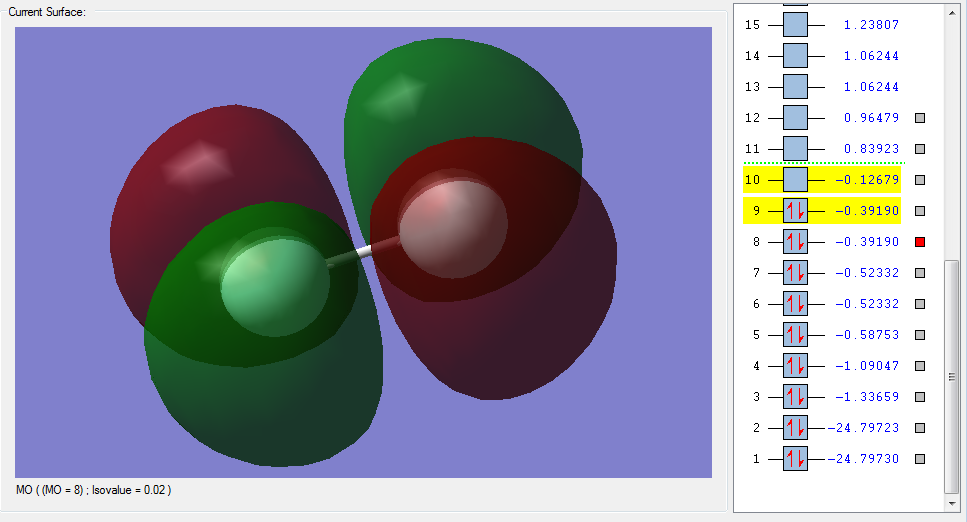
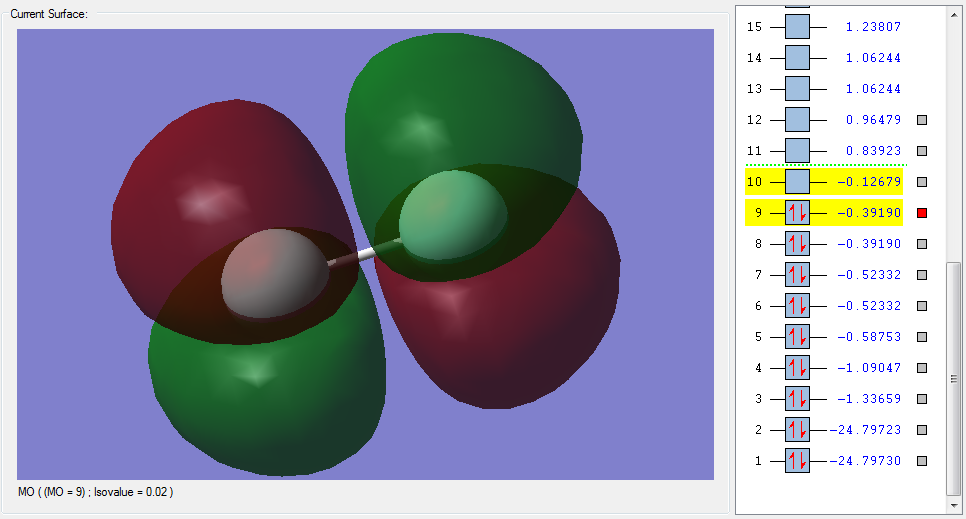
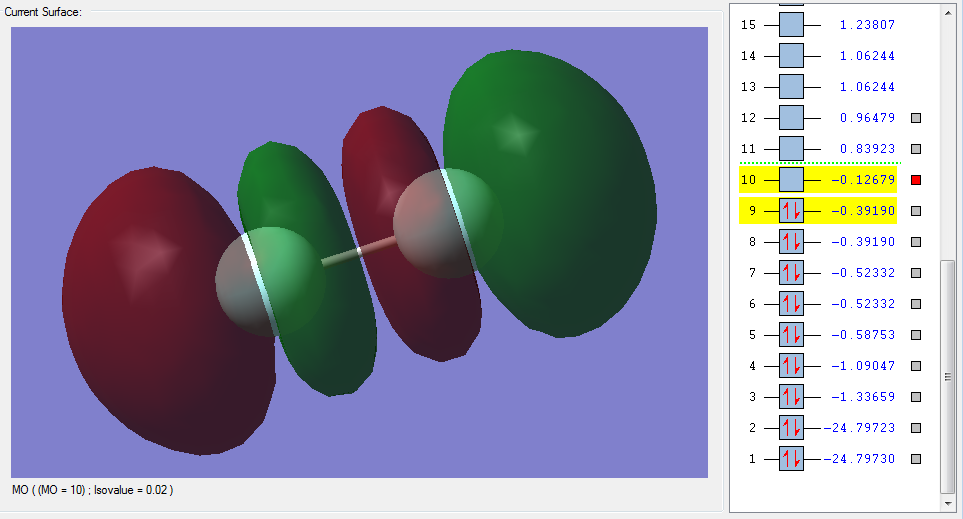
The molecular orbitals
| Shape | Description |
|---|---|
 |
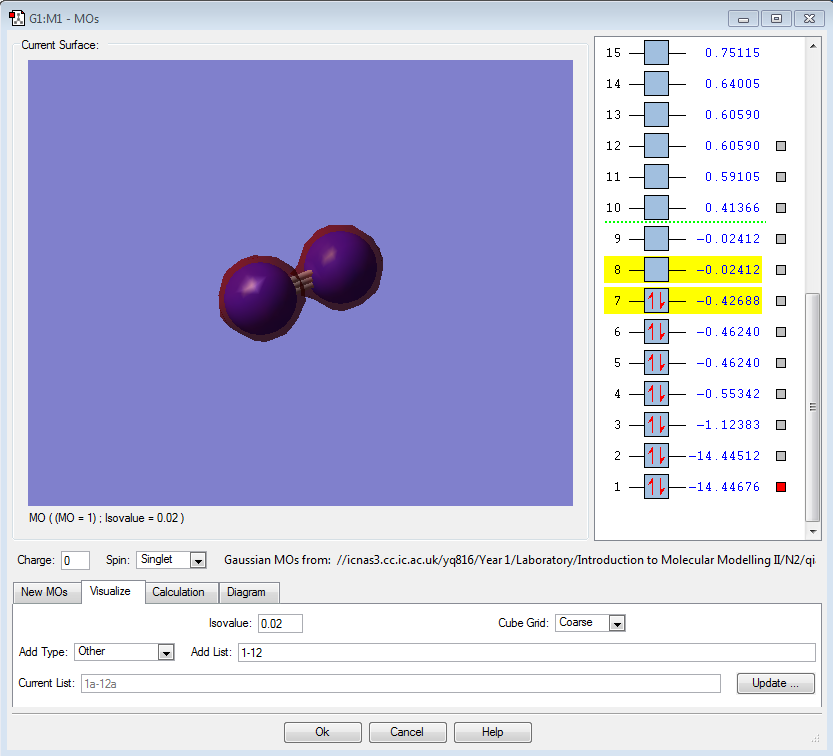σ1s (Non-bonding Orbital) |
 |
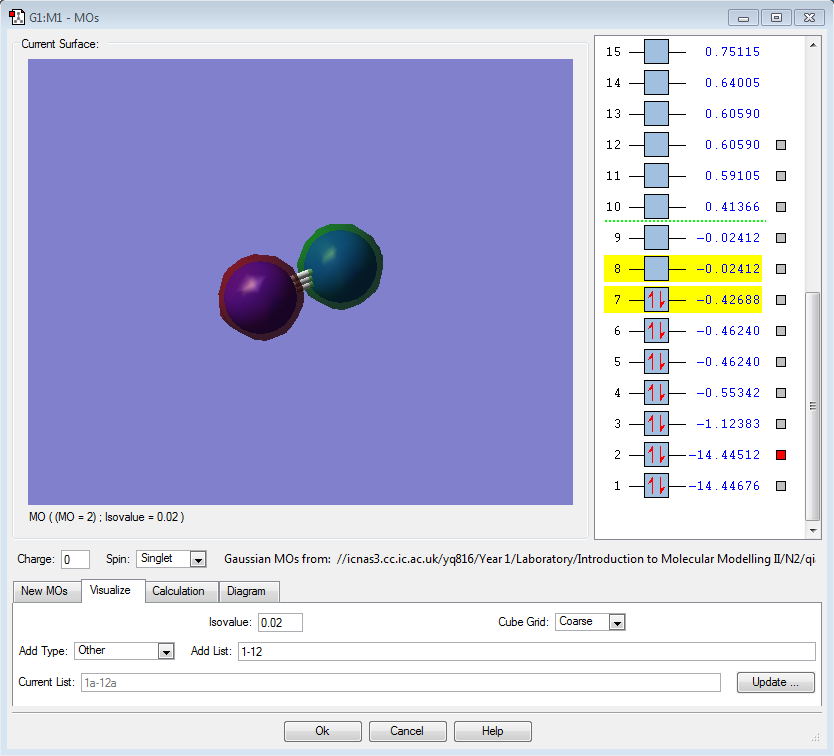σ*1s (Non-bonding Orbital) |
 |
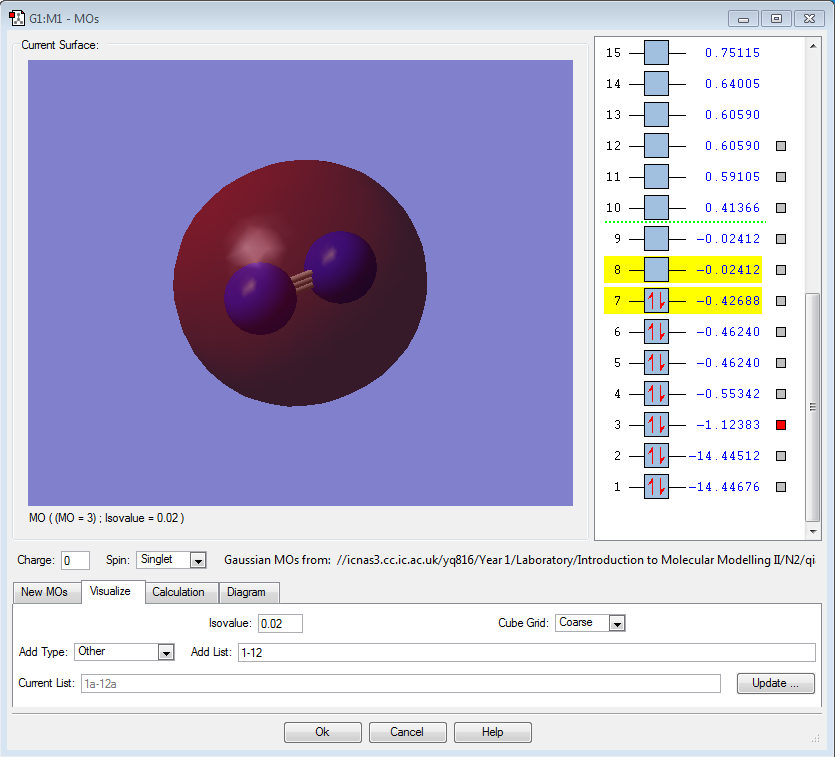σ2s |
 |
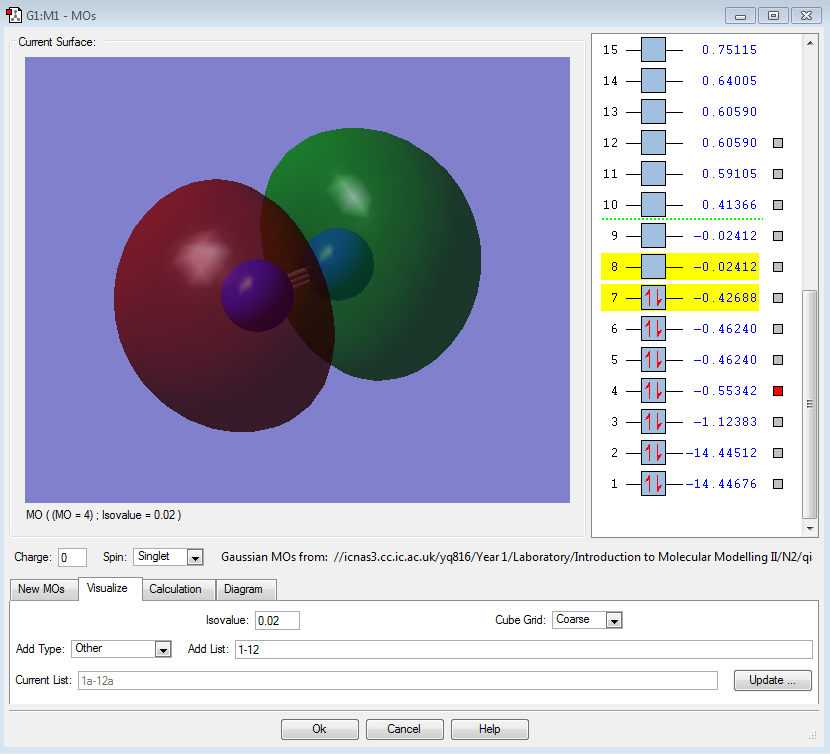σ*2s |
 |
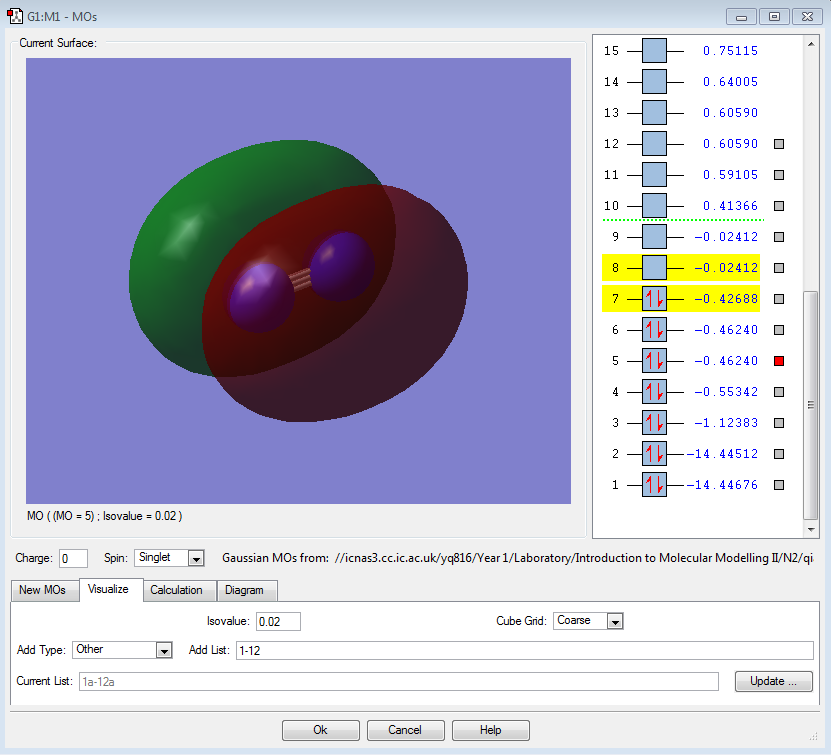π2px |
 |
π2py |
 |
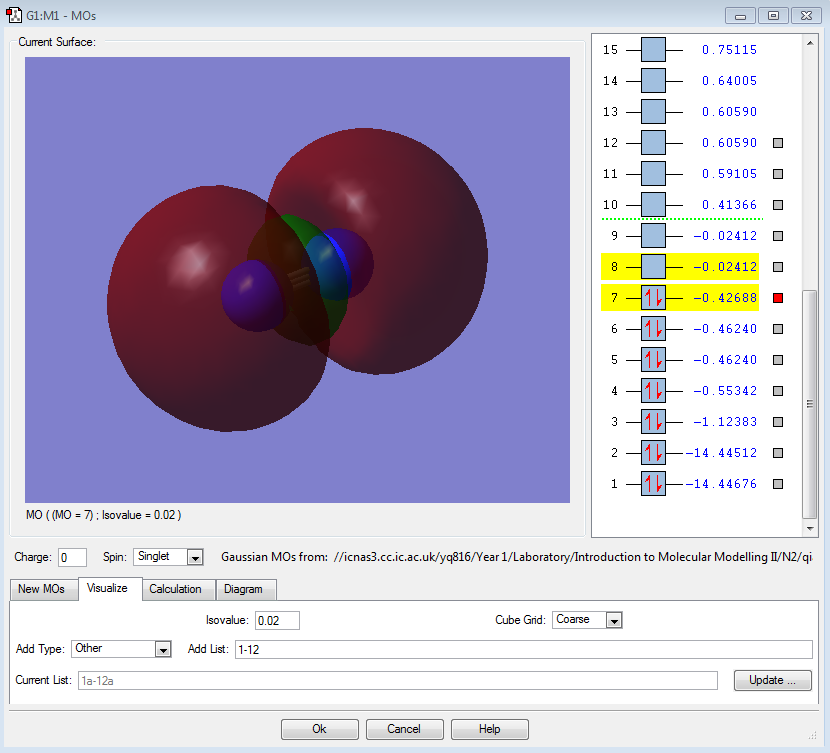π2pz (HOMO) |
 |
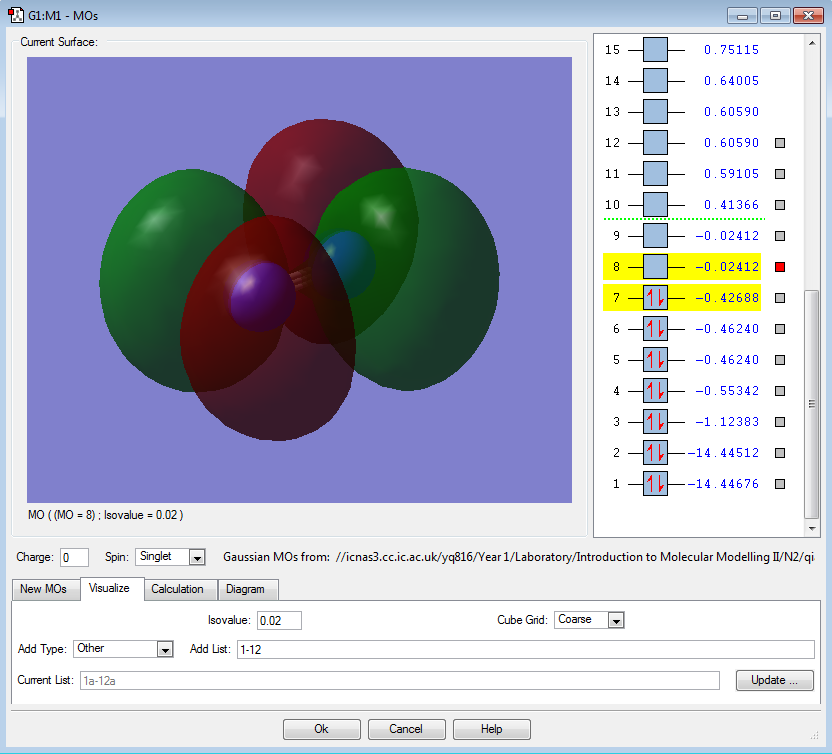π*2px(LUMO) |
 |
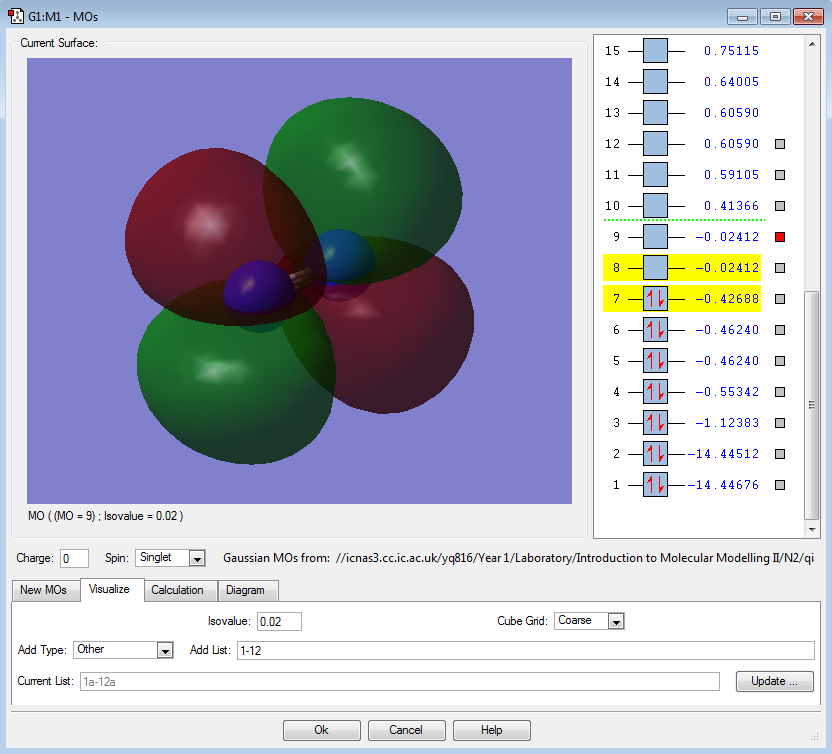π*2py(LUMO) |
The F2 Molecule
Optimisation
The Jmol image of the ammonia molecule |
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -199.49825218 a.u.
RMS Gradient Norm =0.00007365 a.u.
Point Group = D*H
F-F bond distance = 1.40281 Å
The "Item" table:
Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000128 0.000300 YES
Maximum Displacement 0.000156 0.001800 YES
RMS Displacement 0.000221 0.001200 YES
Predicted change in Energy=-1.995025D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4028 -DE/DX = 0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is liked to QIANYIKAI_F2_OPTF_POP.LOG
Vibrations
The fluorine molecule has 2 atoms and is non-linear. Therefore there expected to be 1 modes of vibration from the 3N-5 rule. However, the vibration is completely symmetric, so there is no dipole during the vibration. Therefore, the spectrometer cannot detect the intensity.
Charges
Fluorine is a diatomic molecule. Therefore the charges on the two atoms should be identical.
MOs
| Shape | Description |
|---|---|
 |
σ1s is a occupied non-bonding σg orbital lower than the HOMO. Since non-bonding, it does not give any effect on the overall stabilisation. |
 |
σ*1s is a occupied non-bonding σu orbital lower than the HOMO. Since non-bonding, it does not give any effect on the overall stabilisation. |
 |
σ2s is a occupied bonding σg orbital lower than the HOMO. It is formed by the interaction between the 2s-orbitals of the two fluorine atoms with the same phase. This increase the stability by ΔEs. |
 |
σ*2s is a occupied anti-bonding σu orbital lower than the HOMO. It is formed by the interaction between the 2s-orbitals of the two fluorine atoms with different phases. This decrease the stability by less than ΔEs because the σg orbitals have more similar energy than the σu* orbitals. |
 |
σ2pz is a occupied bonding σg orbital lower than the HOMO. It is formed by the interaction between the 2pz-orbitals of the two fluorine atoms with the same phase. This increase the stability by ΔEpz. |
 |
π2px is a occupied bonding πg orbital lower than the HOMO. It is formed by the interaction between the 2px-orbitals of the two fluorine atoms with the same phase. This increase the stability by ΔEpxy. |
 |
π2py is a occupied bonding πg orbital lower than the HOMO. It is formed by the interaction between the 2py-orbitals of the two fluorine atoms with the same phase. This increase the stability by ΔEpxy. |
 |
π*2pxg is one of the HOMO. This anti-bonding orbital is formed by the interaction between the 2px-orbitals of the two fluorine atoms with the different phase. This decrease the stability by ΔEpxy. |
 |
π*2pyg is another HOMO. This anti-bonding orbital is formed by the interaction between the 2py-orbitals of the two fluorine atoms with the different phase. This decrease the stability by ΔEpxy. |
 |
σ*2pzu is the LUMO. This anti-bonding is not formed so it does not give any effect on the overall stabilisation. |
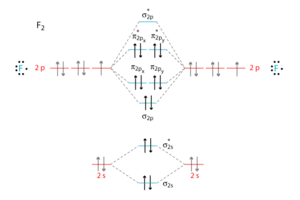
The total stabilisation energy = ΔEpz.
The bond order = 1/2(2-2+2+4-4) = 1.
Therefore, the bond is a single bond.
References
- ↑ NIST Mass Spec Data Center, S.E. Stein, director [Ammonia]
- ↑ A brief summary of the Haber Process [[1]]
- ↑ The molecular orbital energy level diagram of N2 [Molecular orbital energy level diagrams -Hydrogen, Hypothetical, Nitrogen, Oxygen]
- ↑ The bonding and anti-bonding orbitals of F2 [Molecular Orbital Theory]