Rep:Mod:YJY1109
MODULE 1
The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations
Modeling using molecular mechanics
The Molecular Mechanics approach (MM) can be used to study molecular properties in terms of non-quantum mechanical models. MM assumes that energy of a molecule consists of five addictive and non-interactive terms, which are [1]:
- The sum of all diatomic bond stretches
- The sum of al triatomic bond angle deformations
- The sum of all tetra-atomic bond torsions
- The sum of all non-bonded Van der Waals repulsions
- The sum of all electrostatic attractions of individual bond dipoles.
These functions are all mathematically simple and quick to evaluate, and the total energy of a molecule is simply the sum of the five terms. Therefore, MM provides a quick way to minimize the total energy of a molecular system. However, this method has limitations, which are recognised when tackling the problems in section 1.1.
The Hydrogenation of Cyclopentadiene Dimer
Cyclopentadiene dimerises over the course of hours at room temperature via Diels-Alder reaction. Two π systems are involved in Diels-Alder reaction, one contributing 4 π electrons, while the other one contributing 2 π electrons.
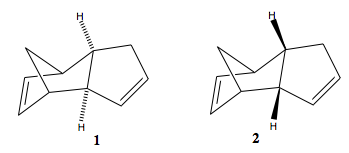
Endo/exo selectivity in the dimerisation of cyclopentadiene
Depending on the orientation the dienophile (in this case, the cyclopentadiene that contributes 2 π electrons) approaches the diene (the other cyclopentadiene that contributes all 4 π electrons), two stereoisomers may be produced, the endo dimer (2) and the exo dimer (1).
The geometries of the two dimers were optimised using the MM2 force field option:
| Energies | Exo dimer (1) | Endo dimer (2) |
|---|---|---|
| Stretch/kcal mol-1 | 1.28 | 1.25 |
| Bend/kcal mol-1 | 20.58 | 20.85 |
| Stretch-Bend/kcal mol-1 | -0.84 | -0.84 |
| Torsion/kcal mol-1 | 7.66 | 9.51 |
| Non-1,4 VDW/kcal mol-1 | -1.42 | -1.54 |
| 1,4 VDW/kcal mol-1 | 4.23 | 4.32 |
| Dipole/dipole/kcal mol-1 | 0.38 | 0.45 |
| Total Energy/kcal mol-1 | 31.87 | 34.00 |
The results show that both isomers have very positive bending energies, which shows the bonds are much more bended than they are in their natural state. The total energy of the endo isomer is lower than the exo isomer by approximately 2.1 kcal mol-1. This difference is mainly due to the difference in torsion energies of the two isomers. Although the endo isomer is less stable, it is known that in this reaction, it is specially formed. This observation can be explained using the Frontier Molecular Oribital (FMO) theory[2]:
 |
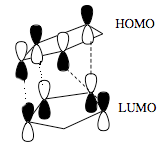 |
In the transition state of the endo addition, there is an additional non-bonding interaction. This secondary orbital interaction does not give rise to a bond, but it contributes to lowering the energy of the transition state with respect to the exo one. The reaction is kinetically controlled.
Hydrogenation of the cyclopentadiene dimer
Hydrogenation of the dimer formed initially gives one of the dihydro derivatives below:
As above, the geometries of the two isomers were optimised using the MM2 force field option:
| Energies | 3 | 4 |
|---|---|---|
| Stretch/kcal mol-1 | 1.24 | 1.13 |
| Bend/kcal mol-1 | 18.78 | 13.01 |
| Stretch-Bend/kcal mol-1 | -0.75 | -0.57 |
| Torsion/kcal mol-1 | 12.72 | 12.41 |
| Non-1,4 VDW/kcal mol-1 | -1.34 | -1.32 |
| 1,4 VDW/kcal mol-1 | 6.05 | 4.44 |
| Dipole/dipole/kcal mol-1 | 0.16 | 0.14 |
| Total Energy/kcal mol-1 | 36.86 | 29.24 |
Both isomers have very positive bending energies, suggesting that the bonds are much more bended than they would be in their natural state. Isomer 3 has a much larger bending energy comparing to isomer 4. This can be accounted for if we calculate the sp2 bond angles in 3 and 4. In isomer 3, the sp2 bond angles are both 107.5°, whereas in the more stable isomer 4, the sp2 bond angles are 112.7° and 112.8°, closer to the ideal 120°. They also have very positive torsional strength, and 1,4 Van Der Waals' Force.
Molecular mechanics predicts that isomer 4 is lower in total energy. This suggests that the hydrogenation of cyclopentadiene proceeds first with hydrogenation of the double bond in the six-membered ring, followed by hydrogenation of the double bond in the five-membered ring.
Click on the links below to see the models of 1,2,3 and 4, minimised by MM2 field option:
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The diagram below shows two isomers 9 and 10, which are both intermediates in the synthesis of Taxol. On standing, one isomer gradually isomerises to form the other isomer. To find out which is the more stable isomer, we can analysis the relative energies of the two isomers using MM2 molecular modeling.
MM2 force field optimisation
Initially, isomer 9 was optimised to have an energy of 58.39 kcal mol-1. However, at this energy, the cyclohexane ring adapts a twist-boat conformation, which is not the most stable conformation of cyclohexane. After manually manipulating the cyclohexane to its more stable chair conformation with bond angle of 109.5°. The energy after optimization is 47.84 kcal mol-1. This is an example of the limitation of MM2: it is able to locate a local minimum, but it will not necessarily find the lowest energy conformation, the global minimum. The global minimum can only be found when the starting structure is close to the lowest energy conformation.
Isomer 10 was optimised to have an energy of 42.68 kcal mol-1. The cyclohexane ring was already in chair conformation, so the molecule is already in its lowest energy conformation.
The results show that isomer 10 is the more stable conformation.Isomer 9 is expected to isomerise to 10 on standing.
To view the lower energy conformation of isomer 9 and 10, click on the links below:
MMFF94 optimisation
The calculation is performed again, this time using MMFF94. The results, along with the results from MM2 calculation, are summarized in the table below.
| Method | Energy of isomer 9/kcal mol-1 | Energy of isomer 10/kcal mol-1 |
|---|---|---|
| MM2 | 47.84 | 42.68 |
| MMFF94 | 70.54 | 60.56 |
Using the MMFF94 method, isomer 10 is still the more stable isomer. However it is important to note that the energy values calculated using different methods cannot be directly compared, as different programs use different parameters in their calculation process.
Hyperstable olefins
It is known that the alkene functional group reacts slowly towards hydrogenation. To rationalize this, the strain energy of the parent alkane of isomer 9 was calculated using MM2 force field, and the resulting energy is 56.93 kcal mol-1. The energy of isomer 9 is 42.68 kcal mol-1.
According to Maier and Schleyer[3], the olefinic strain (OS)is calculated by subtracting the total energy of the most stable conformer of the parent alkane from the total strain energy of the olefin. Therefore, the olefinic strain for isomer 9 is -14.25 kcal mol-1. Similarly, the OS of isomer 10 is -14.62 kcal mol-1. Maier and Schleyer defined olefins that contain less strain than that of their parent hydrocarbon and have negative OS values as "hyperstable" olefines. They are exceptionally unreactive due to special stability afforded by the cage structure of the olefin, as well as the greater strain of the parent hydrocarbon.
Modelling Using Semi-empirical Molecular Orbital Theory
A purely mechanical molecular model has limitations, as illustrated in part 1.1. For example, the secondary orbital interactions in the transition state of Diel-elder reaction is not taken into account in the calculation, and therefore the model failed to explain the endo selectivity of the reaction. Using the alternative method of semi-emirical molecular orbital theory, such electronic aspect of reactivity can be illustrated.
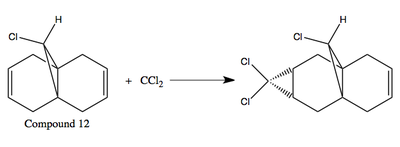
Regioselective Addition of Dichlorocarbene
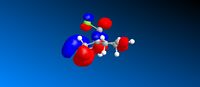
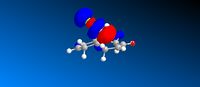
The diene (12) regiospecifically reacts with electrophilic reagents such as dichlorocarbene. To find out the site of attack, the geometry of compound 12 was minimised using MM2, before applying the MOPAC/PM6 method. The MOPAC/PM6 method provides an approximate representation of the valence-electron molecular wavefunction, particularly of the HOMO, presumably the most reactive towards electrophilic attack.
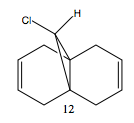 |
Molecular orbitals of compound 12
 |
 |
 |
 |
 |
|---|
Looking at the HOMO of compound 12, it is obvious that the HOMO of the two alkene bonds are different in electron density. The alkene bond that is endo to the chlorine substituent is more electron dense, hence more nucleophilic, than the alkene bond that is exo to the chlorine substituent. Therefore, an electrophilic reagent, such as dichlorocarbene, reacts with the alkene bond exo to the chlorine substituent. Also, the attack is on the less hindered site, which is on the face opposite to the cyclopropyl ring.[4]
The reaction scheme is:
 |
The influence of the C-Cl bond on the vibrational frequencies of the diene
In the crystal structure of compound 12, it was observed[4] that the distance between either of the two exo double bond carbons and the central bridgehead carbon was shorter than the endo distance. In other words, the two rings are distorted. This is a result of the stabilising interaction between the C-Cl σ* (LUMO+2) orbital with the π exo (HOMO-1) orbital. To investigate how the C-Cl bond influences the vibrational frequency of the diene, we compare compound 12 with compound 13, which is a hydrogenated version of compound 12 where the exo double bond is replaced by a C-C single bond.
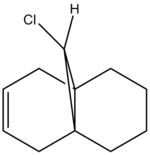 |
The stretching vibrations of various bonds in compound 12 and 13 were calculated using the density function approach, and the results are summarised inn the table below.
| Bond | Compound 12/cm-1 | Compound 13/cm-1 |
|---|---|---|
| C-Cl | 772.5 | 777.0 |
| C=C (endo to Cl) | 1761.0 | 1761.7 |
| C=C (exo to Cl) | 1740.9 | n/a |
The C-Cl vibrational frequency of compound 13 is higher than that of compound 12. This is because the π exo orbital is now absent in compound 13, so there is no more interaction between the C-Cl σ* orbital and the π exo orbital. The interaction between the σ* and π orbitals weakens the C-Cl bond as there is effectively more electron density in the anti bonding orbital. Therefore, when the interaction is lost, the C-Cl bond appears to be a stronger bond with higher vibrational frequency.
[Load up the output LOG or FCHK (you get this from the SCAN) file (into ChemBio3D or Gaussview) and inspect any Cl-C stretching frequencies (see instructions). Look in particular for any with a large IR intensity, and identify the two C=C stretches for the diene and the single C=C stretch for the monohydrogenated derivative. Comment on their values and any differences between the diene and the monoene. If you do spot changes, comment on whether they make sense in terms of your analysis in part one above.]
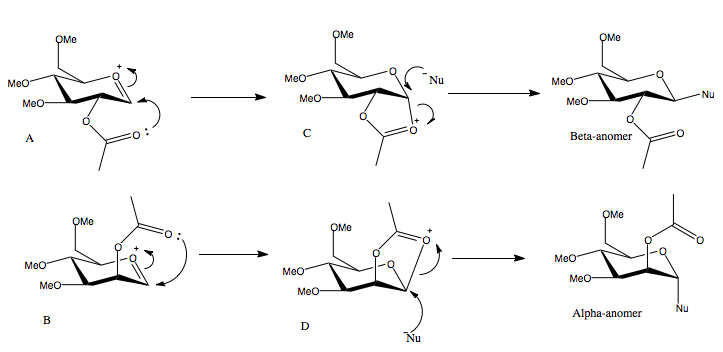
Monosaccharide chemistry: glycosidation
Glycosidation leads to the formation of two anomers, depending on the direction of the acetyl group in the starting material. Below is a graph showing the mechanism of glycosidation:
Industrial productions of oligosaccharides usually require at least 99% yields of the desired stereoisomer. Therefore, in order to reduce side reactions and optimize selectivity, the structure of the transition state, which involves oxacarbenium ion, can be studied. However, this species has short lifetime, so is hard to study experimentally. One way to deal with this problem is to use molecular modeling to estimate their properties.[5] In this study, the structure and property of the intermediate was studied using both MM2 and MOPAC/PM6 methods.
For the R group of the molecule, it was decided methyl group should be chosen. Methyl group is relatively small, with a low electron count comparing to other protecting groups of alcohol, thus minimizing the computational demand. It should be noted that although hydrogen has only 1 electron, it is not a suitable R group as the -OH groups will form inter- and intra-molecular hydrogen bonds, affecting the structure and property of the species being studied.
Although both MM2 and MOPAC/PM6 were used to model the species, it is likely that MOPAC/PM6 will give a more reliable result. This is because MM2 method does not take into account electronic interactions, so some interactions, like neighbouring group effect, are neglected. This will lead to unreliable results as neighboring group effect controls the regioselectivity of the formation of the oxonium ring.
Results of optimization using MM2 and MOPAC/PM6 are summarised in table 1 and 2 below:
| Compounds | Energy/kcal mol-1 (MM2 optimisation) | Energy/kcal mol-1 (MOPAC/PM6 optimisation | Structure (MOPAC/PM6 optimisation | Description |
|---|---|---|---|---|
| A | 26.75 | -58.23 | Structure of A | The acyl group is pointing above the plane of the oxonium cation |
| A' | 37.10 | -67.70 | Structure of A' | The acyl group is pointing below the plane of the oxonium cation |
| B | 33.96 | -67.69 | Structure of B | The acyl group is pointing above the plane of the oxonium cation |
| B' | 37.10 | -63.45 | Structure of B' | The acyl group is pointing below the plane of the oxonium cation |
| C | 37.38 | -88.73 | Structure of C | The oxonium ring is pointing above the plane of the molecule |
| C' | 34.53 | -91.66 | Structure of C' | The oxonium ring is pointing below the plane of the molecule |
| D | 31.82 | -90.51 | Structure of D | The oxonium ring is pointing above the plane of the molecule |
| D' | 29.55 | -87.82 | Structure of D' | The oxonium ring is pointing below the plane of the molecule |
| Energies | Compound A | Compound A' | Compound B | Compound B' | Compound C | Compound C' | Compound D | Compound D' |
|---|---|---|---|---|---|---|---|---|
| Stretch/kcal mol-1 | 2.49 | 2.46 | 2.24 | 2.46 | 1.82 | 2.10 | 1.87 | 2.02 |
| Bend/kcal mol-1 | 13.93 | 14.86 | 14.40 | 14.86 | 18.91 | 14.38 | 15.40 | 13.67 |
| Stretch-Bend/kcal mol-1 | 1.00 | 1.10 | 0.98 | 1.10 | 0.79 | 0.76 | 0.73 | 0.69 |
| Torsion/kcal mol-1 | 2.44 | 0.90 | 1.34 | 0.89 | 9.52 | 9.63 | 9.12 | 7.75 |
| Non-1,4 VDW/kcal mol-1 | -1.56 | -2.18 | -3.00 | -2.18 | -3.70 | -2.39 | -3.08 | -2.63 |
| 1,4 VDW//kcal mol-1 | 18.75 | 17.87 | 18.85 | 17.86 | 17.72 | 17.72 | 17.58 | 17.85 |
| Charge/Dipole/kcal mol-1 | -16.70 | -5.28 | -7.14 | -1.27 | -6.33 | -5.65 | -8.87 | -8.77 |
| Dipole/Dipole/kcal mol-1 | 6.39 | 7.37 | 6.29 | 7.37 | 3.36 | -2.03 | -0.94 | -1.03 |
For A and A', A' is higher in energy, whereas for B and B', B' is higher in energy. The main difference in total energies of A and A' arises due to the difference in charge/dipole interactions, while the main difference in energies of B and B' arises in torsion energy and charge/dipole interactions. The difference is charge/dipole interactions is probably due to the different orientations of the acetyl group (which contains a polar oxygen atom).
Structure based Mini project using DFT-based Molecular orbital methods
Assigning regioisomers in "Click Chemistry"
An azide and an alkyne react via 1,3-cycloaddition to give a 1,2,3-trizole, giving two regioisomeric products, as shown below.
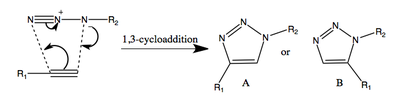
It was reported[6] in 2002 that the rate of the reaction can be greatly increased by using either Cu(I) or Ru (II) catalyst. This reaction quickly found applications in various fields including chemistry, material science and biology. For example, it has been used in activity-based protein profiling (ABPP) of crude proteome homogenates[7] and selective labelling of modified bacterial cell walls[8].
Depending on the catalyst used, different isomers are predominantly formed: the use of Cu(I) catalyst gives mainly isomer A, while the use of Ru(II) catalyst predominantly produces isomer B. The two isomers can be differentiated by 13C NMR.
Take two isomers, where R1 = ph, R2 = -CH2-Ph as an example. The carbons in these 2 molecules are labelled below to aid the discussion.
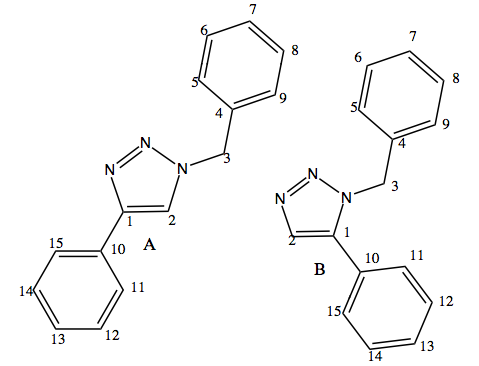
The key spectroscopic difference in isomer A and isomer B would appear in the region of aromatic carbons. For isomer B, a lot of overlapping peaks are expected as the carbons in the two 6-membered rings have very similar chemical environments. Those carbons in isomer A is likely to have a lot of overlapping peaks as well, but the extent would be less than that of B. This is because the two rings are spatially closer to each other in isomer B, hence coupling may easily appear.
| Chemical Shift / ppm | Singlet?Doublet | Degeneracy | Assignment | Discussions |
|---|---|---|---|---|
| 51.7897 | Singlet | 1.0 | 3-C | In literature[6], this peak appears at 51.85 ppm as a single peak. Therefore the calculated spectrum is in good agreement with literature. Carbon 6 does not belong to any aromatic systems in this molecule, and therefore is more shielded than any other carbons in the molecule. |
| 123.022 | Singlet | 1.0 | 1-C | [6]In literature, these peaks overlap with each other, forming a series of multiple peaks. These peaks are all due to carbons in the two benzene rings. This is as expected as they are in similar environments. |
| 123.684 | Singlet | 1.0 | 15-C | Same as above. |
| 124.067 | Singlet | 2.0 | 14-C | Same as above. |
| 124.115 | Singlet | 1.0 | 8-C | Same as above. |
| 124.582 | Singlet | 2.0 | 12-C,10-C | Same as above. |
| 124.607 | Singlet | 1.0 | 6-C | Same as above. |
| 124.925 | Singlet | 1.0 | 5-C | Same as above. |
| 124.993 | Singlet | 1.0 | 7-C | Same as above. |
| 125.10 | Singlet | 1.0 | 9-C | Same as above. |
| 125.452 | Singlet | 1.0 | 16-C | Same as above. |
| 125.761 | Singlet | 1.0 | 11-C | Same as above. |
| 129.012 | Singlet | 1.0 | 4-C | Same as above. |
| 133.428 | Singlet | 1.0 | 3-C | In literature[6], the chemical shift is 133.03 ppm.Thus the calculated result agrees well with literature. However, there is a peak appearing at 135.66 ppm which is not included in the calculated results. |
| 137.32 | Singlet | 1.0 | 2-C | In literature[6], the chemical shift occurs at 138.26 ppm. The calculated result agrees well with literature. |
 |
 |
As mentioned earlier, different catalysts give different isomers in this reaction. Cu(I) catalysts give mainly isomer A, while Ru(II) catalysts give isomer B. To understand this difference, we need to take a look at the mechanism of the reaction.
Mechanism of reaction
L.Zhang, X.Chen et al.proposed a hypothesis for the Ru(II) catalysed reaction:

The proposed mechanism involves oxidative coupling of an alkyne and an azide on ruthenium, which gives a six-membered ruthenacycle. The ruthenacycle undergoes reductive elimination to give the automatic triazole product.
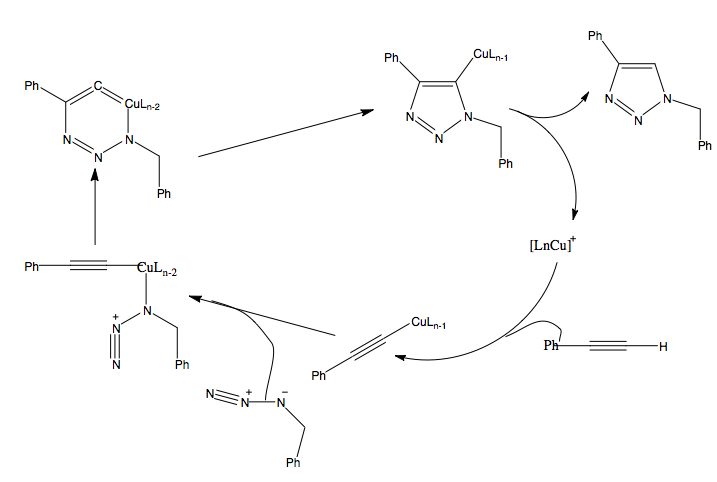
DFT calculations have suggested that the Cu(I) catalyzed reaction proceeds via the following mechanism:
The first step involves the coordination of alkyne to Cu(I), displacing one of the acetonitrile ligands.The next step involves the displacement of another acetonitrile ligand with azide.This activation energy barrier calculated for this step is lower than that direct 1,3-cycloaddition. (http://pubs.acs.org/doi/pdf/10.1021/ja0471525)After this step, the distal nitrogen of the azide attacks the carbon of the acetylide, forming six-membered copper (III) metallacycle. The calculated barrier for this step is enormously lower than that of the uncatalysed reaction, which explains the enormous rate acceleration of the copper (I) catalyzed process. The next step is a ring contraction : the 6 membered ring contracted to a 5-membered ring. Proteolysis of the 5-membered ring releases the final product, completing the catalytic cycle.
Reference
- ↑ "Molecular Mechanics", 3rd Year Undergraduate Computational Chemistry, Imperial College London
- ↑ F.Fringuelli, A.Taticchi, "The Diels-Alder reaction: selected practical methods, 1st edition, 2002, pp.22-24
- ↑ Maier, W. F.; Schleyer, P. V. R, J. Am. Chem. Soc. 1981, 103, 1891. DOI:10.1021/ja00398a003
- ↑ 4.0 4.1 B.Halton,R.Boese and H.S.Rzepa, J. Am. Chem. Soc. Perkin Trans. 2, 1992, 447-448 DOI:10.1039/P29920000447
- ↑ D. M. Whitfield, T. Nukada, Carbohydr. Res., 2007, 342, 1291. DOI:10.1016/j.carres.2007.03.030
- ↑ 6.0 6.1 6.2 6.3 6.4 L.Zhang, X.Chen et al., J. Am. Chem. Soc., 2005, 127, 15998 DOI:10.1021/ja054114s
- ↑ A.E.Speers, G.C.Adams, B.F.Cravatt, J. Am.Chem. Soc, 2003, 125, 4686
- ↑ A.Link, D.Tirrell, J.Am.Chem.Soc., 2003, 125,11164