Rep:Mod:YHphys

Transition State Structures

The Cope Rearrangement

In this section, the Cope rearrangement of 1,5-hexadiene will be used to study a chemical reactivity problem. The objectives are to locate the low-energy minima and transition structures on the C₆H₁₀ potential energy surface and to determine the preferred reaction mechanism using Gaussian. Nowadays it is generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy.

An anti and gauche conformer of 1,5-hexadiene was drawn in Gaussview and cleaned using the Clean function. Then they were optimised at the HF/3-21G level of theory. The anti and gauche conformer were then identified from the appendix 1 in the physical lab wiki page.

Comparison of anti and gauche linkage 1,5-hexadiene using HF/3-21G level of theory

Conformer	Energy/ A.U.	Point group	Structure
Anti 2	-231.69254	Ci	Taxol 11
Gauche 3	-231.69266	C1	Taxol 11

The energies of the anti and gauche conformers were calculated and they show that the gauche conformer is lower in energy by 0.33kJmol^-1, and is more stable. You would expect the anti to be more stable due to less steric repulsion but there is a conformational preference for the gauche which contains a favourable π_C=C/σ*_C-H overlap.

The conformers were then optimised using the B3LYP 6-31G* level of theory.

Comparison of anti2 1,5-hexadiene optimised using different levels of theory

Level of Theory	Energy/ A.U.	Structure	Calculation Time	C-C-C-C angle/°
HF 3-21G	-231.69254		1min14s	180
B3LYP 6-31G*	-234.61170		5min40s	180

The calculation run using the higher level of theory provided a better optimisation but the calculation took longer to run. The better optimisation with B3LYP 6-31G* is seen by a more stable energy conformer, with a more negative energy being found which is equivalent to a difference of 7664 kJ/mol. The C-C and C=C bond lengths are also in agreement with literature bond lengths of 1.54Å for a C-C single bond and 1.34Å for a C=C double bond. On the other hand, the HF 3-21G results differ slightly. There is little difference in the overall geometry of the molecule from both levels of theory and if the accuracy of the Gaussian calculation is considered ~0.01 Å, both calculations give very similar geometry results.

In order to confirm that the high level of theory did indeed find the minimun, frequency analysis was carried out. The frequency analysis is essentially the second derivative of the potential energy surface, if the frequencies are all positive then we have a minimum, if one of them is negative we have a transition state, and if any more are negative then we have failed to find a critical point and the optimisation has not completed or has failed. There were no imaginative frequencies so a minimum had been reached.

Optimising the Boat and Chair Transition State

Two manual approaches in optimising the Chair Transition Structure

The transition optimizations are more difficult than minimizations because the calculation needs to know where the negative direction of the reaction coordinate is. The two approaches used below are to compute the force constant matrix in the first step of the optimisation, method 1, or to use a frozen coordinate method, method 2.

Optimising the Chair Transition State

'	Optimisation to a TS Berny	Frozen Coordinate Method
Transition Structure	tsberny	tsfrozen
Terminal C-C bond length/Å	2.02	2.02
Imaginary Frequency/cm-1	-818	-818
Mode of vibration

The information above shows that the method 1 and method 2 both give the same result and they have both found the transition state. They have found an imaginary frequency of -818cm^-1. When this is animated,it shows that one C-C bond is forming whilst the other is breaking, a asynchronous bond formation. The bond length between the terminal C are 2.02A in both cases. The only difference between the frozen coordinate method and the complete force constant matrix method is the expense of the calculations.

If you start with a reasonable guess for the TS structure, computing the Hessian in the first step will be the easiest way to optimise the structure, with the force constants updated as the optimisation proceeds. The frozen coordinate method involves two steps, firstly freezing the coordinates of the terminal C and minimising this structure, followed by unfreezing the bonds and optimising this to a transition state. It may then not be necessary to compute the whole Hessian, and just differentiating along the reaction coordinate might give a good enough guess for the initial force constant matrix. This is less expensive than the first method.

QST2 method to optimise boat transition state

Using this method, you can specify the reactants and products for a reaction and the calculation will interpolate between the two structures to try to find the transition state between them. The reactant and product was both the anti2 conformer which was minimised in the first part. You need to manually alter the numbering of the reactants and products to make sure they are numbered in the same way.

The numbering process was very time consuming, by going through the atom list and making sure the numbers correspond. The dihedral angle was changed to 0° to make it easier to identify the C. One problem encountered was that the numbering kept altering after I'd changed them and I had to start from the beginning.

The optimisation was run using the option TS(QST2) instead of TS(Berny) for the chair TS optimisations. The first job failed because when the calculation linearly interpolated between the two structures, it did not rotate around the central bonds so it was not able to locate the boat transition structure. This is because the reactant and product structures drawn were too unreasonable. This highlights the problem with the QST2 method. Although it is fully automated, it can often fail if the reactants and products do not closely resemble the transition state. The reactant and product geometries in the original file were modified so that they are closer to the boat transition structure. The C-C-C-C angle to was set to 0° and the inside C-C-C were reduced them to 100°. The job ran to give the following result.

Taxol 11

The the imaginary frequency is visulised, it shows that one bond is forming as the other is breaking, an asynchronous bond formation When looking back at the originally numbered atoms, the C11-C14 bond is breaking and the C1-C4 bond is forming.

Intrinsic Reaction Coordinate

When looking at the chair and boat TS, it is not possible to predict which product they will lead to. However, in Gaussian, the IRC method allows you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface.It creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest until the minimum is reached.

The previously optimised chair TS was used to consider the product it will lead to. The number of points to be considered in the IRC was set at 50.

Comparison of IRC calculations

	Calculate force constants once	Calculate force constants always
Points along the IRC	26	47
Energy	-231.6193220	-231.691667
IRC Pathway
IRC Gradient
Last point of IRC		|

The instructions said to read the force constants from the chk file. However, the job failed to run because the calculation could not find the chk file. Therefore the option calculate force constants once was selected. This made the job more expensive and should not have been necessary since the force constants had already been calculated previously. When the IRC calculation finished, it could be seen that the minimum geometry was not reached. One option was to specify a greater number of points in the IRC and run the calculation again. However, this was not possible as the maximum was set to 50 and the calculation decided it only needed 26 steps. In order to find the minimum, the method chosen was to redo the IRC specifying that you want to compute the force constants at every step. This is the most reliable method but also the most expensive, although it is acceptable for the small system being studied. The IRC gradient when the number of points is 47 has reached 0 so this confirms that the minimum has been reached.

The product found through the more reliable method had an energy of -231.691667a.u., which is identical in energy to the gauche2 conformer in the appendix. This means that the reaction which proceeds through the chair TS goes on to give gauche2 conformer of 1,5-hexadiene.

Activation Energy

Finally, the activation energies for the reaction via both transition structures was calculated. The boat and chair transition state were optimised using B3LYP/6-31G* level of theory. As seen in the optimisation of anti2 1,5-hexadiene, this level of theory provides a better minisation but takes longer to run. The information on zero point and thermal energies were obtained from the Thermochemistry information in the log file.

Method	HF/3-21G			B3LYP/6-31G*
	Electonic energy/a.u.	Sum of electronic and zero point energies at 0K/a.u.	Sum of electronic and thermal energies energies at 298.15K/a.u.	Electonic energy/a.u.	Sum of electronic and zero point energies at 0K/a.u.	Sum of electronic and thermal energies energies at 298.15K/a.u.
Chair TS	-231.619322	-231.466697	-231.461339	-234.556983	-234.414926	-234.409004
Boat TS	-231.602802	-231.450928	-231.445298	-234.543093	-234.402342	-234.396008
Reactant- anti2	-231.692535	-231.539539	-231.532565	-234.611703	-234.469212	-234.461856

Summary of activation energies (in kcal/mol)

	HF/3-21G		B3LYP/6-31G*		Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	34.06	33.17	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.32	44.7 ± 2.0

The boat TS high level optimisation files can be found at DOI:10042/to-2903

The chair TS high level optimisation files can be found at DOI:10042/to-2904

When using the B3LYP/6-31G* level of theory, a better optimised of the transition states is calculated and this decreases their enrgy level. The activation energies calculated using B3LYP/6-31G* are in much better agreement with the experimental values of 33.5 ± 0.5 for the chair TS and 44.7 ± 2.0 kcal/mol for the boat TS.

Results show that the chair transition state is more stable than that of the boat with a lower activation energy of 33.16 kcal/mol at compared to 41.32kcal/mol at room temperature. Therefore, it can be concluded that the reaction mechanism of the Cope rearrangement prefers to proceed via the chair than the boat transition state. The reaction will proceed from the anti2 conformer through the chair TS to the gauche 2 conformer in the Cope rearrangement.

The Diels Alder Cycloaddition

In this part, the transition state of Diels Alder reactions will be charaterised and the molecular orbitals of the reactants studied. The method used will be the frozen coordinate method because this is the least expensive option. The AM1 semi-empirical molecular orbital method will be used for these calculation

The Diels Alder reaction is a cycloaddition reaction. The π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. The nodal properties allow one to make predictions according to the following rule:

Ethylene and Cis Butediene

The frozen coordinate method was used to find the transition state. This was decided because it does not require the initial geometry guess for the transition state to be very exact. It is also the less expensive method as discussed in the section above. The ethylene and cis butediene were first drawn and minimised separately using the AM1 semi-empirical molecular orbital method. The two fragments were then combined and the bond forming length fixed at 2.2Å and minimised. Then this was replaxed and optimised to a TS.

Molecular Orbitals

'	Ethylene	Cis Butediene	Transition State
LUMO
Symmetry with respect to plane	Anti-symmetric	Symmetric	Symmetric
HOMO
Symmetry with respect to plane	Symmetric	Anti-symmetric	Anti-Symmetric

It can be seen that the HOMO of the ethylene+cis butadiene transition structure is generated from the the HOMO of cis butediene and the LUMO of ethylene. On the otherhand, the LUMO of the transition state is derived from overlap of the cis butediene LUMO and ethylene HOMO. This is consistent with the conservation of orbital symmetry which stated that the symmetry of the orbital formed from the overlap of the two orbitals must be the same as the orbitals from which it is derived.

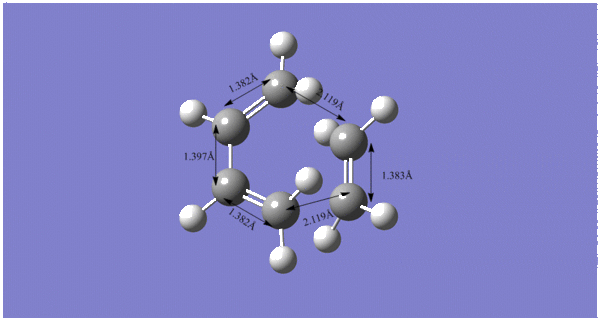
The labelled diagram contains all the C-C bond lengths in the transition state. The literature values for typical sp3 and sp2 C-C bondlengths are 1.54Å and 1.33Å respectively. The vdW radius of C is 1.70Å. The bond distance between the C that will form the C-C single bond is 2.119Å. This is smaller than double the C vdW radius which implies that the C atoms are within vdW radii of eachother and a bond will bond. The bond has not completely formed in the TS.

When frequency analysis was carried out on the structure, an imaginary frequency at -956cm-1 was found. This implies that a transition state has been reached. The displacement vector is shown and it can be seen that the formation of the two bonds is synchronous, i.e. they occur in the same step.

The lowest positive frequency shows the ethylene molecule vibrating. There is no bond forming or breaking. It is simply a low energy vibration which could take place at room temperature.

Cyclohexa-1,3-diene reaction with maleic anhydride

Cyclohexa-1,3-diene undergoes reaction with maleic anhydride in a cycloaddition reaction to give primarily the endo adduct. The reaction is kinetically controlled so the endo isomer is expected to be lower in energy compared to the exo transition state. This will be investigated and the reason behind the endo adduct being favoured will be explained. Again the frozen coordinate method will be used with the C-C bond forming distances fixed at 2.2Å. When the geometry was relaxed and the optimisation to a BernyTS carried out, the additional keywords "opt=noeigen" were used. Once the first transition state was optimised,it was found to be the exo form so the geometry was altered to give the endo form.

exo file: https://www.ch.ic.ac.uk/wiki/index.php/Image:TSfirsttry.chk endo file: https://www.ch.ic.ac.uk/wiki/index.php/Image:2endooptfreq.chk

The endo and exo adduct were identified by the orientation of the Hs on maleic anhydride. In the endo adduct, the dienophile H are pointing up whereas in the exo adduct, the corresponding H are pointing down.

Molecular Orbitals

'	Exo adduct	Endo Adduct
LUMO
HOMO
Energy (AM1)/a.u.	-0.05041982	-0.05150480
Energy (B3LYP/6-31G*)/a.u.	-612.6793109	-612.68339703

Discussion of strain in exo adduct

The exo TS is higher in energy than the endo adduct by 10.7kJ/mol as calculated by the B3LYP/6-31G* level of theory. The energy difference calculated by the AM1 method is 2.85kJ/mol. The difference in energy calculated by both methods is expected to be the same but the energies calculated by Gaussian have an error ~5kJ/mol. The energy difference can be rationalised with comparison of strain within the molecules. The C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” carbon fragments on the diene are shown in the diagrams below. The C-C bond forming distance is also shown. Endo adduct on the left, exo adduct on the right.

It can be seen that there is greater steric strain in the exo adduct. There the electrons are close in space and the resulting repulsion could destabilise the molecule. The C-C distances of interest are shorter in the endo adduct, which would imply more steric strain. However, in the exo adduct, there are two such interactions of interest and the vicinal H on the CH2-CH2 fragment are found below the plane and in the space of the maleic anhydride. This is the source of strain in the exo adduct and disfavours the exo form. However, there is also another effect that favours the endo form, secondary orbital overlap.

Secondary Orbital Overlap

The new bonds are forming between C8-C13 and C1-C4 and these orbitals are active in forming the new bond. Secondary orbital overlap is defined as the positive overlap of a nonactive frame in the frontier molecular orbitals of a pericyclic reaction. The orbital diagram is based on overlap between cyclopentadiene and maleic anhydride. It is given to illustrate which orbitals interact with other through space in secondary orbital overlap. In the endo adduct, there are more orbitals involved which leads to greater stabilisation of the transition state.

All the following images show the HOMO

endo adduct nodal plane

endo adduct secondary orbital overlap

exo adduct nodal plane

exo adduct no secondary orbital overlap

The two images on the left show the endo adduct HOMO but the isovalue to visulise the MOs was decreased from 0.02 to 0.01. The nodal plane can clearly be been in the diagram and it runs through the centre -(C=O)-O-(C=O)- of the maleic anhydride and CH2-CH2 fragment of the cyclohexa-1,3-diene. Both endo and exo HOMO are antisymmetric with respect to the nodal plane. There is an interaction between the C p orbitals of the -(C=O)-O-(C=O)- fragment, C1 and C4, with the C p orbitals of in the cyclohexa-1,3-diene C8, C9, C10 and C11. On inspection, it is seen that the electron density is shared between the πC=C system of the cyclohexa-1,3-diene and passes through the back of the molecule to the π*C=O orbital on maleic anhydride. This secondary overlap stabilises the endo TS and thus lowers its activation energy. There is no secondary orbital overlap visible in the exo HOMO.

Conclusion

Through this lab course, I have been able to optimise transition state structures. Three different methods were used and I now understand the advantages and disadvantages of each to make an informed decision about which method to use in different situations. In addition, molecular orbitals of the transition states were visualised and through orbital overlap, the reaction could be further understood.

---

References and citations