Rep:Mod:YB3JVVC0M3

Conformational analysis using Molecular Mechanics

A Brief Introduction To Molecular Mechanics and the MMFF94s Method

Born out of a desire to accurately model the conformations of large molecular structures such as proteins with a view towards drug design and ligand-acceptor models in biological systems, molecular mechanics (MM) is the study of the molecules using classical mechanics. At the time of its inception, ab initio computational methods were in their infancy and severely limited by the computational power available, not a concern for the relatively simple MM methods. The classical treatment of molecules relies on a number of assumptions:

• Atoms (nuclei and electrons) are considered as perfect impenetrable spheres.
• Each atom has a specific radius and charge based on known values.
• The bonds between atoms are considered as springs between two spherical masses.

Using these assumptions the potential energy of a molecule is modeled as the sum of a series of contributions, corresponding to both covalent and non-covalent interactions. Most MM methods were developed to model a specific area in chemistry in agreement of empirical data, and so use different parameter values (such as equilibrium bond lengths) and terms are often included in the potential energy.

The MMFF94s force field was developed to accurately model protein ligand-acceptor interactions. This includes finding molecular geometries, conformational minima and crucially molecular dynamics simulations of ligand and acceptor association and dissociation. These parameters were prioritized over those not commonly used in the analysis of proteins - the MMFF94s method poorly models the splitting of vibrational modes as these are reported to minimally alter the protein interactions under investigation. This is typical in the development of MM methods: all models more accurately describe some properties at the cost of others.

The potential energy values produced by MMFF94s calculations have little real world significance, but highlight a molecular geometries deviation away from the ideal reference values used in the calculation. To use an example, a large positive bond stretching energy would be representative a large increase in bond lengths relative to the ideal bond lengths used in the method. A low bond stretching energy would be indicative of near ideal bond lengths in the molecule at that particular geometry.

The Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene (henceforth CPD) is known to dimerise at room temperature to form dicyclopentadiene(DCPD). Dicyclopentadiene then undergoes a reverse diels alder reaction upon heating to afford cyclopentadiene. Dicyclopentadiene can exist as two isomers, and these have been investigated using molecular mechanics calculations.

MMFF94s Calculations for Dicyclopentadiene

	Endo		Exo
Parameter	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)
Bond Stretching Energy	3.46791	5.959562597	3.54297	6.398314428
Angle Bending Energy	33.18863	57.0	30.77229	55.6
Stretch Bending Energy	-2.08220	-3.58	-2.04136	-3.69
Torsional Energy	-2.94986	-5.07	-2.73060	-4.93
Out-Of-Plane Bending Energy	0.02184	0.0375	0.01500	0.0271
Van Der Waals Energy	12.35928	21.2	12.80143	23.1
Electrostatic Energy	14.18508	24.4	13.01376	23.5
Total	58.19067		55.37349

The table above shows the results of the forcefield calculations of the two known isomers of DCPD. The endo structure is very slightly greater in energy than the exo form, and so less thermodynamically stable. This can be attributed to the bond angle bending and Van der Waal energies. The total energy found using force field calculation is the sum of the individual components seen above. Although absolute values can be compared for each component the relative contribution of each term towards the total energy is a value that enables comparison of structures that cannot be compared using absolute values, such as homologous series of compounds.

If DCPD formation was a thermodynamically controlled process, then exo-DCPD would be the major product. This is not the case however with the endo form dominating. The dimerisation is therefore kinetically controlled with secondary orbital overlap being responsible for the stability of the endo forming transition state.

Hydrogenation of endo-DCPD is found to yield two products with Tetrahydrodicyclopentadiene (THDCPD) only being formed using vigorous reaction conditions. For comparison forcefields were calculated for (3),(4) and THDCPD. THDCPD would be expected to be the least strained and so the lowest energy; the inclusion of sp² carbon centres in structures (3) and (4) results in increased ring strain as seen by the increased the angle bending energy. Interestingly the initial hydrogenation products have significantly differing energies, with (4) being more stable and closer in energy to THDCPD than (3).

MMFF94s Calculations for DCP Hydrogenation Products

	(3)		(4)		THDCPD
Parameter	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)
Bond Stretching Energy	3.30689	6.519536193	2.8231	6.842636331	2.68756	7.069798862
Angle Bending Energy	30.85475	60.83016349	24.68538	59.83248133	22.64378	59.56591483
Stretch Bending Energy	-1.92573	-3.796578184	-1.65717	-4.016652491	-1.51556	-3.986777733
Torsional Energy	0.07038	0.138754224	-0.37833	-0.916997132	3.30168	8.685280889
Out-Of-Plane Bending Energy	0.01508	0.029730232	0.00028	0.000678665	0	0
Van Der Waals Energy	13.28043	26.18237802	10.63721	25.78249428	10.8972	28.66578315
Electrostatic Energy	5.12098	10.09601603	5.14702	12.47535902	0	0
Total	50.72278		41.25749		38.01466

Isomer (4) would be expected to be the major product in a thermodynamically controlled hydrogenation reaction, as it is the lower energy of the two hydrogenation products. The fact that TFDCPD is only produced after prolonged hydrogenation is indicative of the hydrogenation reaction being under kinetic control. If the reaction was under thermodynamic control, then the distribution of products would be dependent on product stability and so THFCPD would be the major product, followed by (4) and then (3). This suggests that (3) is the quickest forming isomer, and so the product of the hydrogenation.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

An intermediate in the synthesis of Taxol is well known for it's atropisomerism; a sufficiently large steric barrier between conformers leads to isomers that are isolable. In the case of the intermediate, the isomers feature the carbonyl group pointing up or down. Furthermore, the structure of the isomers is dependent upon the conformation of the fused cyclohexane ring. The chair and twist boat structures of cyclohexane are energy minima, and so it can be postulated that the lowest energy conformation of intermediates (9) and (10) could feature either of these structures. Work by Paquette et al. suggests that the structure of the conformation of the cyclodecanone (ring A) and cyclohexane (B) rings are dependent, with the 'up' carbonyl resulting in a twist boat structure in the cyclohexane ring, whilst the 'down' conformer has a chair cyclohexane structure. This is a result of the oxy-cope rearrangement by which these two species were experimentally observed. For completeness the two corresponding hypothetical structures were also optimised using force field calculations.

MMFF94s Calculations for Taxol Intermediates (9) & (10)

	Isomer (9)				Isomer (10)
	Chair Conformer		Twist Boat Conformer		Chair Conformer		Twist Boat Conformer
Parameter	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)
Bond Stretching Energy	7.7117	10.93130798	7.95977	10.43411225	8.75355	11.69036645	9.05169	11.06328238
Angle Bending Energy	28.33218	40.16076679	29.53933	38.72180791	22.21561	29.66894823	26.21994	32.04689956
Stretch Bending Energy	-0.05678	-0.080485453	0.08263	0.108316031	-0.20132	-0.26886287	-0.0638	-0.077978523
Torsional Energy	0.06738	0.095510916	2.71409	3.557781156	5.873	7.843391785	6.31715	7.72103489
Out-Of-Plane Bending Energy	0.96193	1.363532435	0.95078	1.246335666	1.60571	2.144425783	1.49886	1.831957505
Van Der Waals Energy	33.23016	47.10363643	34.72251	45.5162105	36.25716	48.42143894	38.21536	46.70810854
Electrostatic Energy	0.30034	0.425730907	0.31692	0.415436483	0.37461	0.500291673	0.5782	0.706695642
Total	70.54691		76.28603		74.87832		81.8174

There are a number of interesting comparisons that can be made between these four structures. The first is between conformers of the same isomers. In both cases the twist boat conformers are higher in energy than the chair conformers. This can be attributed to the increased angle bending energies and torsional energies. In isomer (9) the dihedral angle of 62^o in the chair conformer is reduced to a more straining 36^o in the twist boat form, with a similar reduction from 58^o to 37^o seen in isomer (10).

This in itself is not surprising; cyclohexane is found to have a dihedral angle of 56^o and 31^o in the chair and twist boat forms respectively; these conformations would naturally have different torsional energies. For both (9) & (10) the change in energies shows the same trend for every parameter except torsional and angle bending energies. The contribution of torsional energy to the total energy of (9) is dramatically increased in the twist boat form, with the angle bending energy increasing marginally; its contribution falls in relative terms. The inverse is true for (10) where its torsional energy increases very slightly (and also falls in relative terms), with the angle bending energy contribution increasing in both a real and relative sense.

This strongly suggests that the conformation of the carbonyl group influences the geometry of the neighboring ring B corroborating previously reported experimental findings. The changes in these two parameters result in small but noticeable energy differences for each conformer, with the relative contributions of the torsional and angle bending parameters differing by a few percentage points at best.

For all conformers the two largest factors in determining the stability of the molecules are Van der Waal (VdW) interactions and angle bending energies. Large VdW energies indicate that the distances between many atoms in the molecule are shorter than optimum, and these through space interactions are destabilising. VdW interactions are modelled using a 7-14 potential model, and the large values found for conformers of (9) and (10) indicate that the sum of repulsive interactions between non-bonded atoms in the structures are significantly larger than the attractive interactions. Angle bending energies represent the deviation of bond angles from known equilibrium values. In the case of (9) and (10) large angle bending energies are indicative of bond angles throughout the molecule being significantly smaller or larger than expected.

The taxol intermediates (9) and (10) are examples of anti-Bredt structures, exhibiting an unusual stability in the presence of a bridgehead alkene.

Generally bridgehead alkenes are known to be unstable in polycyclic structures, as observed in Bredt's rule. Bredt's rule is an empirical observation that double bonds will not form on the bridgehead of bridged ring systems. The justification for this is the introduction of strain and misalignment of orbitals. In small rings (generally considered to be less than 8 carbons) a bridgehead alkene introduces large amounts of angle strain as planarity of the alkene cannot be preserved. This is mirrored electronically with a destabilisation of the π system, as the sp² P orbitals become nearly orthogonal.

Molecules that do feature bridgehead alkenes, so called 'Anti-bredt' structures have been enticing to both theoretical and synthetic chemists alike. Force field calculations on some hypothetical anti-Bredt structures showed negative strain energies; the structures with bridgehead alkenes were supposedly more stable than the hydrocarbon from which their structure was derived.

The hypothetical bridgehead structures that exhibited negative strain energies were found to contain medium to large rings but that the stability did not increase infinitely with ring size. The stability was found to be derived from the stability of their corresponding trans-cycloalkenes. In small rings, the energy difference between cis and trans isomers can be very large, to the point where the trans-alkene does not form. As ring size increases however, the energy difference between isomers falls and the trans isomer is more favoured relative to the cis. This energy difference decays non-linearly, to a point where increasing the ring size only marginally decreases the energy difference between the isomers.

Spectroscopic Simulation using Quantum Mechanics

The GIAO basis set was developed to overcome mathematical limitations in computationally determining chemical shifts. Experimentally determined NMR chemical shifts are recorded by exposing a sample to an external magnetic field, and this field can be expressed as a potential with a defined origin. The applied magnetic field is said to be independent of the origin chosen. Theoretically however this is not the case with finite basis sets resulting in chemical shift values that are dependent upon the origin of the magnetic field. To overcome this, a new basis set was constructed that is dependent on the magnetic field, making the chemical shifts independent of the magnetic field origin, hence Gauge Invariant Atomic Orbitals.

Spectroscopy of an intermediate related to the synthesis of Taxol

Experimental NMR data has been previously reported for two derivatives of the atropisomers (9) & (10). These derivatives were again used by Paquette et al. to demonstrate the atropselective oxy-cope rearrangement, and can be assumed to by synthesised by the same mechanism. The structure of these two atropisomers is therefore analogous to the conformations of (9) and (10), with the less stable (17) featuring the carbonyl 'up' and ring B in a twist boat conformation.

MMFF94s Calculations for Taxol Intermediates (17) & (18)

	Isomer (17)				Isomer (18)
	Chair		Twist Boat		Chair		Twist Boat
Parameter	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)	Value(kcal/mol)	Relative Contribution(%)
Bond Stretching Energy	15.95524	22.61649731	15.96446	20.92710815	15.70425	20.97302664	16.73864	20.45853327
Angle Bending Energy	31.5094	44.66446511	31.75867	41.63104306	25.84063	34.51016262	27.93994	34.14914187
Stretch Bending Energy	0.28788	0.408068901	0.35668	0.467556117	-0.01517	-0.020259536	0.16794	0.205261961
Torsional Energy	11.02855	15.63293134	13.31955	17.46001201	17.09348	22.82834337	18.13996	22.17127408
Out-Of-Plane Bending Energy	1.20293	1.705149099	1.14636	1.502712882	1.70564	2.277882303	1.93863	2.369459308
Van Der Waals Energy	52.0317	73.75475411	53.49446	70.12353376	52.5209	70.1416645	56.38837	68.91977746
Electrostatic Energy	-7.21053	-10.22090124	-6.87572	-9.013078804	-7.00902	-9.360546551	-6.96596	-8.514032467
Total	104.80517		109.16446		105.84071		114.34752

As with isomers (9) and (10), the conformation of the cyclohexane rings have been deduced from the stabilities of each isomer in different conformations. Experimentally, isomerisation of (17) to (18) was afforded by heating in THF for five days, a clear indication that the process proceeds thermodynamically. With this in mind, ring B cannot be adopting a twist boat conformation as this has the highest energy; the conformer of (18) must be lower in energy than the conformer of (17) from which it isomerised. Furthermore, the chair conformer of (17) is the most stable of isomers and so would not readily isomerise thermodynamically to either conformations of (18). This leaves one combination of conformers, twist-boat (17) isomerises to chair (18).

With theoretical and experimental observations in agreement, the NMR spectra of isomer (18) were calculated. The structure was first optimised at the B3LYP/6-31G(d,p) level, then the spectra computed using the GIAO method. Interestingly, optimisation of the proposed twist-boat conformer of (18) at the same level yields the chair conformer, possibly suggesting that the chair conformer is a global energy minima.

At first glance the experimental and theoretical results to show similar values for ¹H NMR. The theoretical spectrum shows a similar range to the experimental. Some of the proton environments with simpler splitting can be assigned to the experimental data, however these do not necessarily agree with the theoretical results. The theoretical NMR spectrum assigns individual protons to the peaks which they derive however these fail to agree with the experimental results for all but a handful of environments.This is because the method condenses peaks of similar chemical shift into one degenerate peak provided the calculated shifts are within a 0.05ppm tolerance. This is a problem as many of the environments are chemically similar and this leads to protons on either sides of the molecule being grouped into a peak with an integral of three - this is not representative of the actual integration due to magnetic equivalence. Furthermore computed NMR spectra ignore averaging due to thermal motion. This means that chemically equivalent protons which are magnetically equivalent at room temperature are interpreted as being static and thus magnetically inequivalent. The multiplicity of the peaks due to spin-spin coupling can be calculated using another method, however this is computationally intensive and so was not found.

Experimental and Calculated ¹³C NMR data for Taxol Intermediate (18)

Experimental	Calculated DOI:10042/26496
Chemical Shift δ(ppm)	Chemical Shift δ(ppm)
211.49	210.88
148.72	143.00
120.90	122.44
74.61	92.66
60.53	65.30
51.30	58.11
50.94	54.11
45.53	50.47
43.28	44.43
40.82	42.91
38.73	41.40
36.78	38.20
35.47	36.20
30.84	31.20
30.00	28.76
25.56	24.97
25.35	24.41
22.21	24.38
21.39	23.74
19.83	23.27

Experimental and Calculated ¹H NMR data for Taxol intermediate (18)

Experimental			Calculated DOI:10042/26496
Chemical Shift δ(ppm)	Integration	Multiplicity	Chemical Shift δ(ppm)	Integration
5.21	1	m	5.54	1
3.00-2.70	6	m	3.22, 3.08, 3.08, 3.00, 2.71	6
2.70-2.35	4	m	2.44, 2.30, 2.20, 2.05	4
2.20-1.70	6	m	1.87	6
1.58	1	t	1.57	1
1.50-1.20	3	m	1.87, 1.87, 1.57	3
1.10	3	s	1.57, 1.45, 1.12	3
1.07	3	s	1.12, 1.12, 0.95	3
1.03	3	s	0.95, 0.95, 0.54	3

The taxol intermediates of interest, (9),(10),(17) and (18) have been most intensively studied by Paquette in a number of papers. One problem has been consistently overlooked by Paquette and of vital importance given the heavy reliance of computationally optimised structures in the discussion of their atropisomerisation. In the theoretical determination of the lowest energy structure, both boat and chair forms have been considered. What was not considered is the orientation of the spiro cyclohexane ring with respect to the rest of the structure; for each molecule there could not only exist a boat or chair form, but two boat and two chair forms. Although both experimental and theoretical work has been done on the intermediates, primary interest remains with their novel atropisomerism and little else.

The experimental evidence used to initially determine the structure of the intermediates (17) and (18) is insufficient to determine which chair, or which boat form of the spiro ring is most stable. Paquette solely relies on nuclear overhauser effect (NOE) coupling between methyl groups to rationalise his choice of structure - at best this resolves the boat/chair structures, but not which boat or chair. This is because the distance between methyl groups only varies due to conformation and not orientation; in both chair forms the methyl groups in question are the same distance apart and go exhibit the same amount of through space coupling. Aside from NMR spectra, the only other evidence is a computer-generated structure of an X-ray diffraction of a related intermediate and this is definitely insufficient to deduce in which orientation the cyclohexane ring would be most stable in.

Analysis of the properties of the synthesised alkene epoxides

Stereoselective epoxidation of alkenes is known to be possible using (amongst others) two catalysts, the Shi and Jacobson catalysts. Three aspects of the epoxidation of trans-β-methyl styrene and trans-stillbene can be investigated computationally; the catalysts, transition states and products.

The Shi Catalyst

General Structures of Shi Catalysts

Shi catalysts are an important class of organic catalyst used in the stereoselective epoxidation of alkenes. Their structures are fructose derived with functionalisation differing dependent on alkene type - cis, trans or terminal. Development of chiral ketone organocatalysts primarily focused on the epoxidation of trans alkenes with catalysts for cis alkenes being developed as an alternative to the Jacobson catalysts. Shi catalysts suitable for trans-alkenes will catalyse cis-alkene epoxidation albeit at with poor selectivity; it has been reported that the epoxidation of cis-β-methyl styrene lead to a 39% ee (enantiomeric excess) . The epoxidation is known to occur at the carbonyl oxygen, with both the spiro and fused ring stabilising the transition state.

The crystal structure of the Shi catalyst presents some interesting features. Cyclohexanone structures have a conformational profile more complex than simple cyclohexanes. The presence of an sp² carbon in the ring lowers the energy difference between the boat and chair conformers as does functionalisation of the ring. In many cases the energy difference between conformers is sufficiently small that more than two forms exist at equilibrium . Ring B exists in a chair-like form and deviations from the idea chair structure can be attributed to a number of factors. The fused ring A occupying the axial and equitorial positions on adjacent carbons introduces strain; in glucose the dihedral angle is 54.6^o but 36.0^o in the catalyst. This is because the five member ring is much less flexible and must adopt either an envelope or half-chair conformation (both ideally isoenergetic). In this case the ring adopts a half-chair structure, at this comes at the cost of strain in ring B. In contrast the conformation of the spiro ring C is less dependent on ring B and so can adopt either conformation.

Carbon-oxygen bond lengths vary between half-chair and envelope forms, in particular in ring C. With ring C in the half-chair form, the C-O bond lengths a and b are 139 and 134pm respectively. Bond b in particular is surprisingly short with C-O bonds with some double bond character (such as those seen in carboxylic acids) being around 138pm long. This suggests some extra stabilisation of the C-O bond not present in the envelope form of ring C. Furthermore in the envelope form the bond lengths are both 140pm. Both of these contrast to experimental and theoretical C-O bond lengths in free 2,2-dimethyl-dioxolane, in which a and b were computed to be 153pm and found to be 143pm.

In both envelope and half-chair cases, the bond lengths of a and b suggests the competition of two anomeric effects.

The endo-anomeric effect (typically known as just anomeric effect) is the antiperiplanar alignment of a lone pair from a substituent inside the ring with an antibonding orbital from a ring-bound substituent. This results in the strengthening (and so shortening) of the C-O bond as bond assumes more p character, whilst the bond between the ring and the substituent weakens (and so lengthens).

The exo-anomeric effect is primarily seen in carbohydrate derived structures, with the lone pair from a substituent outside the ring donating into an anti-periplanar C-O σ^* orbital. In this case the opposite is true; the ring C-O bond weakens as the lone pair exo to the ring aligns with the ring C-O σ^* orbital, and the C-X bond exo to the ring (in our case C-O) strengthens.

The Shi catalyst is reacted with an oxidising agent to form the reactive species; a dioxirane. Three factors can be considered in the geometry of the transition state:

• The alkene - Which face of the alkene reacts with the dioxirane?
• The dioxirane - Which oxygen is transferred in the epoxidation reaction?
• Side chains - How are the substituents orientated with respect to the catalyst?

These factors culminate in two generally reported transition state (TS) structures for epoxidation, one spiro and another planar. The preference of a reaction to proceed by either TS has appeared to be highly dependent on the structure of the catalyst and substrate, but with the spiro form being favoured in most cases. This can be attributed to alkene π*-oxygen lone pair overlap that is only present in the spiro TS structure. It has been found that only when the spiro TS features very disfavourable steric interactions does the planar TS dominate.

In total eight possible spiro TSs were calculated for each substrate. One possible method of proposed transition state comparison is their energies. The TS with the lowest energy is the most stable and the reaction should proceed with that given geometry. Catalsyt/substrate orientation is the only variation between possible TSs and so it naturally follows that their energies are very similar. Another approach to rationalising the TS through which the reaction proceeds is to analyse the steric interactions between the catalyst and substrate.

Jacobsen's Catalyst

An alternative epoxidation catalyst to Shi's is Jacobsen's catalyst, a manganese transition metal catalyst.In 1990 Katsuki and Jacobsen reported the epoxidation of alkenes using Mn(Salen) derivatives . The Salen ligand - a tetradentate planar ligand can readily be functionalised to attain the desired reactivity and selectivity. It was found that Mn(Salen) catalysts showed good selectivity for terminal and cis-alkenes (up to 93% ee), but relatively poor selectivity for trans-alkenes. The structure of the Mn(Salen) compelexes are well known with the tetradentate ligand coordinating at equatorial positions whilst leaving the axial sites free. In the active form of Jacobsen's catalyst, the two axial positions are occupied by a chloride ion and oxygen, with the chloride ion possibly facilitating oxygen transfer through the trans effect.

Functionalisation of the Salen backbone appears key in affording stereoselective transformations as the backbone itself is planar. Jacobsen's original catalyst features two tert-butyl groups bound to the aryl portions of the ligand. These two groups can rotate in one axis, and come into very close contact across the face of the catalyst. The interactions between the bulky groups can be considered as either repulsive or attractive.

Repulsive interactions between the tert-butyl groups could be stabilised by the rigid nature of the Salen ligand. Significant orbital overlap between the complex π system of the Salen ligand and the maganese centre would be lost if any region of the ligand showed significant deformation. This destabilisation is likely much larger than that resulting from the close contact of the tert-butyl groups, and for this reason steric hindrance is tolerated. The rigidity of the backbone is also reinforced by the fused cyclohexane ring on the opposite face of the ligand. In order to maximise the distance between the tert-butyl groups, the buckling of the planar backbone will also distort the conformation of the cyclohexane ring away from the stable chair form. These electronic and steric factors force the backbone to remain planar and the tert-butyl groups to be in close proximity.

Attractive forces between the groups can be attributed to dispersion forces. The distance between the groups is sufficiently large that the C-H, H-H and C-C Van der Waal interactions are attractive and not repulsive, however in all cases are slightly larger than the ideal Van der Waal radii. If the interaction between the groups was attractive the stability of the ligand would be greatest in its planar form.

The Epoxidation of Trans-β-methylstyrene

Non-Covalent Interaction (NCI) calculations are derived from a known correlation between computed electron density(ρ) and reduced density gradient(s), a parameter that describes deviation from normal electron distribution in a system. Analysis of plots of ρ vs s for molecules whose bonding has been well studied has lead to regions of the plot being associated with different types of bonding, be it covalent, ionic or hydrogen bonds. This known association between ρ, s and types of interactions make NCI calculations useful for inspecting bonding in molecules or systems. NCI surfaces represent non-covalent attractive and repulsive forces between atoms, and this leads to surfaces being generated for both intra and intermolecular interactions. Two factors are important in the calculated NCI surfaces; the area and the colour of the surface. The area of the surface is important as it determines the regions of the molecule where the interactions are felt. The colour of the surface represents the sign and magnitude of the interaction, ranging from strongly repulsive (red) to strongly attractive (blue). A large blue NCI surface between the molecules is indicative of strongly attractive interactions throughout the system.

Sum of Electronic and Thermal Free Energies For Possible Trans-β-methylstyrene Transition States (kcal/mol)

TS	R,R Product	S,S Product
1	-1343.02297	-1343.017942
2	-1343.029272	-1343.015603
3	-1343.032443	-1343.023766
4	-1343.019233	-1343.024742

The NCI surfaces for the TSs loosely agree with the their energy values however any comparisons are subjective and qualitative; the higher energy TSs generally have smaller NCI surfaces with more yellow (mildly repulsive interactions) and less blue/green (attractive interactions). General trends can be seen in the relationship between NCI surface and energy; the more stable TSs feature mildly attractive interactions between as many alkene substituents as possible whilst also prioritising the more stabilising groups. For example TS (7) features a relatively strong attractive interaction between the oxygen in ring B and alkene methyl protons. The orientation that enables this close contact also maximises the distance between the catalyst and the aryl group of the substrate, and as a result this stabilising interaction is lost. Conversely the two most stable catalyst-substrate geometries feature stabilising interactions between the aryl ring and methyl protons.

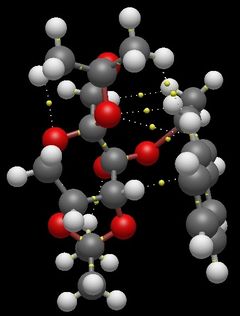
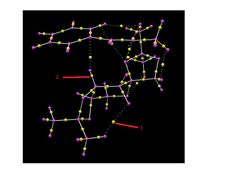
QTAIM is an alternative model useful for interpretting interactions between the substrate and catalyst. QTAIM maps electron density(ρ)to molecular structure. Electron density is greatest at nuclei and so local maxima define nuclei positions. Saddle points in ρ, known as bond critical points (BCPs)are indicative of bonding and location of BCPs in a system generally infers an interaction. It is important to note however that the existence of BCPs in a system does not necessarily confirm bonding, with the NCI model currently being preferred for its model of hydrogen bonding. Nonetheless, a number of important BCPs exist in the most stable transition state and these mirror the NCI surfaces generated. A number of important BCPs exist between the spiro ring (C) of the catalyst and allyl and aryl protons in trans-β-methylstyrene. Both protons appear to interact with a ring oxygen, as well as an exocyclic methyl proton. Further BCPs exist between the substrate and catalyst at either ends of the molecule, qualitatively confirming that this transition state structure maximises overlap/interaction between the substrate and catalyst.

The lowest energy transition state is transition state 3, with the product having R,R stereochemistry. The enantiomeric excess (ee) is a measure of the enantiopurity of a chiral sample. In this case the undesired S,S product is forms when the substrate reacts with the catalyst from the other face. The free energy difference between the two transition states can then be used to determine the ratio of products, and from this the ee. In the case of transition state 3, an relative ee value of 99.99% is obtained. While the the Shi catalyst is known for performing epoxidations with high ee values, selectivity is highly dependent on substrate.

The Product

With the geometry of the theoretical epoxidation product inferred through the orientation of the catalyst in the transition state, the structure and stereochemistry of the product can be compared with experimental results.

Experimental and Calculated ¹H NMR data for Trans-β-methylstyrene epoxide

Experimental			Calculated
Chemical Shift δ(ppm)	Integration	Multiplicity	Chemical Shift δ(ppm)	Integration
7.27	5	m	7.50,7.50,7.49, 7.42, 7.33	1
3.55	1	d	3.45	1
3.12	1	dq	2.74	1
1.43	3	d	1.70, 1.62, 0.75	1

Experimental and Calculated ¹³C NMR data for Trans-β-methylstyrene epoxide

Experimental	Calculated
Chemical Shift δ(ppm)	Chemical Shift δ(ppm)
137.7	134.8
128.3	123.94, 123.23
127.9	122.6,122.5
125.4	118.4
59.4	61.6
58.9	60.2
17.8	19.0

The calculated NMR spectra for trans-β-methylstyrene epoxide is largely in good agreement with the experimentally reported results. One significant problem is the lack of time-averaging magnetic equivalence due to thermal motion; in the experimentally recorded proton spectrum the three methyl protons produce a time averaged signal, whereas the calculation only considers their static positions with respect to the rest of the molecule. Averaging the calculated methyl proton shifts produces an average of 1.36ppm, sufficiently close to the reported value of 1.43ppm.

The Epoxidation of Trans-Stillbene

Sum of Electronic and Thermal Free Energies For Possible Stillbene Transition States (kcal/mol)

TS	R,R Product	S,S Product
1	-1534.687808	-1534.68344
2	-1534.700037	-1534.685089
3	-1534.699901	-1534.693818
4	-1534.687252	-1534.691858

Just as for trans-β-methylstyrene, the epoxidation of trans-stillbene using a Shi catalyst proceeds through analogous spiro transition states and their stabilities can be compared to determine through which the reaction is most likely to proceed to. Transition state 2 is most favoured in the orientation to give a product with R,R stereochemistry. NCI analysis of the transition state draws parallels to the transition state of trans-β-methylstyrene epoxidation. Both feature favourable interactions between the phenyl groups of the substrate and the catalyst. The trans-stillbene transition state features stronger attractive interactions between ring oxygens and the substrate, whereas for methylstyrene a larger portion of the interactions are C-H and C-C derived.

Experimental and Calculated ¹H NMR data for R,R Trans-stillbene Oxide

Experimental			Calculated
Chemical Shift δ(ppm)	Integration	Multiplicity	Chemical Shift δ(ppm)	Integration
7.38-7.30	10	m	7.37-7.19	10
3.87	2	s	3.20	2

Experimental and Calculated ¹³C NMR data for R,R Trans-stillbene Oxide

Experimental	Calculated
Chemical Shift δ(ppm)	Chemical Shift δ(ppm)
137.1	153.4
128.5	142.2
128.3	141.2
125.5	139.8
62.8	76.9

The calculated proton NMR is largely in agreement with experimental results, but the carbon NMR shows a significant deviation of over 15ppm in some cases. This could largely attributed to the basis set and method used; the NMR spectra were computed at the B3LYP/6-31G(d,p) level to reduce calculation time, and this greatly impacts accuracy.