Rep:Mod:Y3PHYSJW1
Cope rearrangement
The Cope rearrangement was discovered by Arthur Cope and it is a [3,3]-sigmatropic shift reaction involving the migration of an allyl group.[1] There has been much work into the mechanistic pathways through which the rearrangement proceeds which are reported to be either radical based or via an aromatic transition state. It is generally accepted that the cope rearrangement of 1,5-hexadiene proceeds through a concerted mechanism, proceeding through a 6-membered transition state. The are two possible transition state geometries are chair conformation and the boat conformation. It has been reported in literature that the chair form is more stable due to the energy stabilisation afforded by the aromatic nature.[2] Whereas the boat transition state is non-aromatic. In this assignment we will be investigating the Cope rearragement of 1,5-hexadiene which is a thermally allowed six electron suprafacial process. We aim to find and optimise the geometries of the most stable conformers of 1,5-diene using Gaussian and then model the transition states leading to these products.
Optimising the Reactants and Products
Preliminary optimisation using HF/3-21G theory

Using Gaussview, 1,5-hexadiene was drawn and optimised at the HF/3-21G level of theory to find the lowest energy conformation. The first conformation invested was one with an anti-perplanar (app) conformation of the middle 4 C atoms of the 6 carbon chain. This was enforced by using the dihedral angle tool in Gaussview and setting it to 180°. The optimisation of the molecule yielded a conformer with Ci symmetry, corresponding to the anti2 conformer (referral to the computational appendix table 1.1). By orientating the terminal alkene bond in different orientations, whilst keeping the app conformation of the middle 4 atoms, also yielded another app conformer but with C1 symmetry. This correpsonds to anti4.
In the second optimisation procedure, a conformation with the middle 4 C atoms in gauche conformation was drawn by setting the dihedral angle to 60°. Optimisation of the structrue gave a higher energy conformation with C1 symmetry, corresponding to gauche3. The gauche conformer obtained was higher in energy relative to that obtained using app conformation of the middle 4 C atoms. Furthermore, the gauche conformer was also obtained with C2 symmetry. It was expected that the gauche conformers would be higher energy relative to the app conformers because in gauche conformation, there is an increase in steric hindrance, thus the increase in energy destabilises the molecule.
The difference in energy of the 1,5-hexadiene conformers under investigation are determined from 3 key energy factors: σ/σ* overlap, electron bond-bond repulsion and intramolecular VdW interactions. The anti conformations are particularly low in energy due to the maximum of σ/σ* orbital overlap that is possible in the anti-periplanar arrangement. Furthermore, it can be seen that the Gauche3 conformer has the lowest energy (-231.69266) out of the 4 conformers formed, and surprisingly lower energy than the anti conformations. This phenomenon is perhaps due to the particular structural geometry of the conformer which enhances the VdW attractive interaction between the terminal alkene groups and possibly enabling the orbital overlap of π/π* overlap between the alkene groups thus offering additional stabilisation. On the other hand, the Gauche conformer, is much higher in energy (-231.68772) due to destabilising repulsion of the terminal groups which are in very close proximity in this gauche conformation.
| Optimisation summaries of confomers | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Anti2 .log file | Anti4 .log file | Gauche3 .log file | Gauche .log file | ||||||
| Jmol File |  |
 |
 |
 | |||||
| File Type | .log | .log | .log | .log | |||||
| Calculation Type | FOPT | FOPT | FOPT | FOPT | |||||
| Calculation Method | RHF | RHF | RHF | RHF | |||||
| Basis Set | 3-21G | 3-21G | 3-21G | 3-21G | |||||
| Charge | 0 | 0 | 0 | 0 | |||||
| Spin | Singlet | Singlet | Singlet | Singlet | |||||
| Total Energy / a.u. | -231.69254 | -231.69097 | -231.69266 | -231.68772 | |||||
| RMS Gradient Norm / a.u. | 0.00002322 | 0.00000659 | 0.00000917 | 0.00000588 | |||||
| Dipole Moment | 0.0000 | 0.2955 | 0.3401 | 0.4556 | |||||
| Point Group | Ci | C1 | C1 | C2 | |||||
| Job CPU time | 3.0 secs | 36.0 secs | 37.0 secs | 1 min 7.0 secs | |||||
It was ascertained that the optimisation were all run successfully by examination of the RMS Gradient Norm which are are all low values. Furthermore, this was further confirmed as the set of forces and displacements associated with the optimisation of the molecule all went to convergence, shown by the 'item' tables, shown below. The convergence of the forces and displacements show that they converged to approximately to a value of 0 and thus small displacement changes of the atoms in the structure shows negligible energy change as the energy of the structure corresponds to an energy minima.
From conducting the frequency analysis on each of the optimised conformers, it was further confirmed that all 4 conformers were optimised to reach the energy minima as the low frequencies are all relatively small (majority are within the limits of ±15 cm-1 and the real frequencies were all positive values.
| Conformer | Item table | Frequencies |
|---|---|---|
| Anti2 |
Item Value Threshold Converged?
Maximum Force 0.000066 0.000450 YES
RMS Force 0.000014 0.000300 YES
Maximum Displacement 0.000343 0.001800 YES
RMS Displacement 0.000128 0.001200 YES
Predicted change in Energy=-3.596292D-08
Optimization completed.
-- Stationary point found.
|
Low frequencies --- -8.3532 -2.8073 -1.6141 0.0005 0.0006 0.0007 Low frequencies --- 71.3359 85.6520 116.1103 |
| Anti4 | Item Value Threshold Converged? Maximum Force 0.000017 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000815 0.001800 YES RMS Displacement 0.000272 0.001200 YES Predicted change in Energy=-1.042342D-08 Optimization completed. -- Stationary point found. |
Low frequencies --- -3.1800 -1.1202 0.0006 0.0006 0.0006 0.5829 Low frequencies --- 86.1381 98.5781 153.6921 |
| Gauche3 | Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.001058 0.001800 YES RMS Displacement 0.000262 0.001200 YES Predicted change in Energy=-1.620934D-08 Optimization completed. -- Stationary point found. |
Low frequencies --- -2.2133 -0.8667 -0.0005 -0.0001 0.0004 1.0557 Low frequencies --- 74.5817 105.0221 130.4965 |
| Gauche | Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.001665 0.001800 YES RMS Displacement 0.000336 0.001200 YES Predicted change in Energy=-8.607611D-09 Optimization completed. -- Stationary point found. |
Low frequencies --- -0.0007 -0.0004 0.0005 0.8639 1.3484 1.9227 Low frequencies --- 113.9527 137.4285 152.3234 |
Further optimisation using B3LYP/6-31G(d) theory
The Anti2 conformer found and optimised in the previous section, was further optimised using the DFT method at a higher level of theory, namely B3LYP/6-31G*. The reported energy of the optimised conformer using this higher level of theory is -234.61170. This absolute energy is lower than that found using the HF/3-21G method, which was -231.69254. Although the individual absolute energies seem quite different, they cannot be compared relative to each other because the calculation method used in each calculation are different. The Hartree-Frock(HF) and Density Functional Theory(DFT) uses different assumptions, approximations and calculations in the optimisation method, therefore it is unappropriate to compare now. Besides, the basis set used in this case, 3-21G for HF and 6-31G(d) for DFT, are 2 different levels of accuracy so again is inappropriate to compare.
| Optimisation summary of Anti2 conformer | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Anti2 .log file | |||||||||
| Jmol File |  | ||||||||
| File Type | .log | ||||||||
| Calculation Type | FOPT | ||||||||
| Calculation Method | RB3LYP | ||||||||
| Basis Set | 6-31G(d) | ||||||||
| Charge | 0 | ||||||||
| Spin | Singlet | ||||||||
| Total Energy / a.u. | -231.61170 | ||||||||
| RMS Gradient Norm / a.u. | 0.00001314 | ||||||||
| Dipole Moment | 0.0000 | ||||||||
| Point Group | Ci | ||||||||
| Job CPU time | 47.0 secs | ||||||||
Again, the reported RMS Gradient Norm value of the optimisation was low and all forces and displacements converged concluding that the optimisation was successfully. This is further emphasised by the positive real frequencies from the frequency analysis. A point to note is that one of the reported low frequencies are outside the generally accepted limits of ±15 cm-1. This can be improved by using a tight convergence command. The real vibrational frequencies are all positive values, indicating that the optimisation has indeed reached a minimum.
| Conformer | Item table | Frequencies |
|---|---|---|
| Anti2 | Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000216 0.001800 YES RMS Displacement 0.000078 0.001200 YES Predicted change in Energy=-1.574258D-08 Optimization completed. -- Stationary point found. |
Low frequencies --- -18.7357 -11.7160 0.0005 0.0006 0.0008 1.7785 Low frequencies --- 72.7233 80.1416 120.0175 |
Comparing the optimised structures from HF/3-21G and B3LYP/6-31G(d) method
On comparison of the two optimised structures using the different computational methods, it can be observed that the bond lengths and bond angles do not differ much. What seems to be clear is that the single C-C bonds are longer based on the HF/3-21G calculation, whereas the double C=C bonds are longer for the B3LYP/6-31G* level of theory. This is illustrated in the table below, where for the C1-C2 double bond, the DFT method gives a bond length of 1.33 Å whereas the HF method gives a bond length of 1.32 Å. Furthermore, the bond angles between each set of 3 carbon atoms, as listed below, are all calculated to be larger using the DFT method at the B3LYP/6-31G(d) level of theory. Besides this, the set of bond lengths and bond angles confirms that the molecule has Ci symmetry.

| Bond | HF method / Å | DFT method / Å | Bond angle | HF method / ° | DFT method/ ° |
|---|---|---|---|---|---|
| C1-C2 | 1.32 | 1.33 | C1-C2-C3 | 124.8 | 125.3 |
| C2-C3 | 1.51 | 1.50 | C2-C3-C4 | 111.4 | 112.7 |
| C3-C4 | 1.55 | 1.55 | C3-C4-C5 | 111.4 | 112.7 |
| C4-C5 | 1.51 | 1.50 | C4-C5-C6 | 124.8 | 125.3 |
| C5-C6 | 1.32 | 1.33 |
Summary of energies
In addition, a list of four important energies can be seen under the Thermochemistry section from the frequency analysis. The first is the sum of electronic and zero-point energies, which correspond to the potential energy at 0K and the zero-point energy (E = Eelec+ZPE). The second is the energy contribution from the translational, rotational and vibratiinal energy modoes at 298.15K and 1 atm (E = E + Etrans + Erot + Evib). The third of which, includes correction for room temperature (H = E + RT ) and the last includes contribution from entropy (G = H - TS).
In order to run the optimisation and frequency at 0K, the keywords "temperature=0.001" was used. This set the temperature conditions of the calculation at approximately 0K. As expected, at approximately 0K, the only energy associated with the molecule is the intrinsic electronic energy and the zero point energy, with no further energy contributions from thermal energies or enthalpies. This is illustrated by the fact that all 4 reported energies are equal to the value of Sum of electronic and zero-point energies, -234.469212 a.u. .
The infrared spectrum from the frequency analysis is shown.
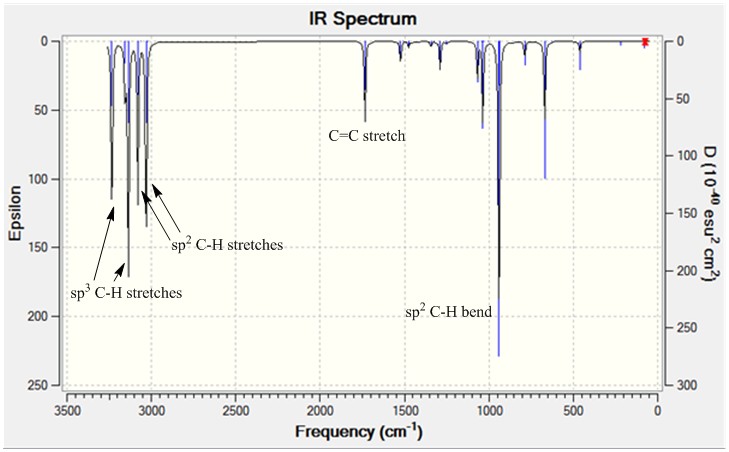
Optimising the boat and chair transition states
In the Cope rearragement of 1,5-hexadiene exists two possible transition states: the chair form and boat form. The transition states were computed using three different methods. The first of which was the Hessian method, where the force constants were computed at the beginning of the calculation. The second method was the fixed coordinate method which uses the Redundant Coordinate Editor function in Gaussian. The last method used the QST2 method. This method works by firstly specify the reactants and products for a reaction and the calculation interpolates between the two structures to try to find the transition state between them.
Ally fragment building blocks
Two allyl fragments were used as the building blocks for the optimisation of the two tranistion states. The fragments used were firstly optimised using the HF method and 3-21G basis set. The optimised structre had C-C bond lengths of 1.39 Å and a C-C-C bond angle of 124.3°.
| Optimisation summary of allyl fragment .log file | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Jmol File |  | ||||||||
| File Type | .log | ||||||||
| Calculation Type | FOPT | ||||||||
| Calculation Method | UHF | ||||||||
| Basis Set | 3-21G | ||||||||
| Charge | 0 | ||||||||
| Spin | Doublet | ||||||||
| Total Energy / a.u. | -115.82303955 | ||||||||
| RMS Gradient Norm / a.u. | 0.00001314 | ||||||||
| Dipole Moment | 0.00015764 | ||||||||
| Point Group | C1 | ||||||||
| Job CPU time | 11.0 seconds | ||||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000324 0.000450 YES RMS Force 0.000097 0.000300 YES Maximum Displacement 0.001254 0.001800 YES RMS Displacement 0.000531 0.001200 YES Predicted change in Energy=-5.245575D-07 Optimization completed. | ||||||||
Chair transition state
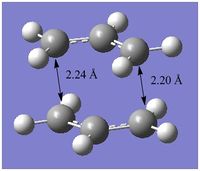
Two copies of the pre-optimised ally fragment was rotated manually to form the chair-like transition state guess structure. The terminal C atoms on each of the allyl fragments were placed approximately 2.20 Å apart. Two methods were used to locate and optimise the chair transition state: the Hessian method and Freeze coordinate method. Evaluation of the results from both methods shows that both arise at the same transition state with one imaginary frequency, although a different method of calculation is used. The imaginary frequency at 818cm-1 correpsonds to the characteristic vibration of the transition state in the Cope rearragement.
Hessian method
The Hessian method was first used in attempt to obtain the chair transition state. A gaussian calculation was setup for a Opt+Freq job and optimised to a TS(berny) with force constants calculated once using the method and basis set HF/3-21G. Additionally, the keyword opt=noeigen was used to prevent the calculation from crashing if more than one imaginary frequency is detected during the optimisation. The summary of the calculation is shown below:
| Optimisation summary of chair transition state using Hessian method .log file | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Jmol File |  | ||||||||
| File Type | .log | ||||||||
| Calculation Type | FREQ | ||||||||
| Calculation Method | RHF | ||||||||
| Basis Set | 3-21G | ||||||||
| Charge | 0 | ||||||||
| Spin | Singlet | ||||||||
| Total Energy / a.u. | -231.61932223 | ||||||||
| RMS Gradient Norm / a.u. | 0.00004533 | ||||||||
| Dipole Moment | 0.0005 | ||||||||
| Point Group | C1 | ||||||||
| Job CPU time | 8.0 seconds | ||||||||
| Imaginary frequency / cm-1 | -817.83 | ||||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000119 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.001649 0.001800 YES RMS Displacement 0.000567 0.001200 YES Predicted change in Energy=-2.468296D-07 Optimization completed. -- Stationary point found. | ||||||||
The calculation was relatively quick since only a single calculation was done, however a good guess structure was required to locate the optimised transiton state.
The optimised structure had terminal C atoms of each allyl fragment was optimised to have a distance of 2.02Å apart and a C-C-C bond angle of 120.5°. The transition state was animated to find a imaginary frequency of -818cm-1, which corresponds to an asymmetrical motion of the chain of six carbons forming and breaking. This is characeristic of the Cope rearragement. Furthermore, to confirm the the optimisation of the transition state was successful, the RMS Gradient Norm was checked to be low and the set of forces and displacements in the Item table was shown to have converged thus signifying that a stationary point was found.
Frozen Coordinate Method
The frozen coordinate method was then used on the guess structure formed from the optimised allyl fragments. In the first step of the calculation, the 4 atoms involved in the bond breaking and formation were frozen using the 'Redundant Coordinate Editor' function. This allows the unfrozen part of the molecule to be optimised using the method and basis set: HF/3-21G. The advantage of this method is that it is often not necessary to compute the whole Hessian and thus time-consuming calculations involved in optimizing complex transition structures can be avoided.
Once optimised, the second step of the calculation involved performing an opt+freq operation on the optimised fragments to optimise it to a transition state. The summary is shown below.
| Optimisation summary of chair transition state using frozen coorindate method .log file | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Jmol File |  | ||||||||
| File Type | .log | ||||||||
| Calculation Type | FREQ | ||||||||
| Calculation Method | RHF | ||||||||
| Basis Set | 3-21G | ||||||||
| Charge | 0 | ||||||||
| Spin | Singlet | ||||||||
| Total Energy / a.u. | -231.61932200 | ||||||||
| RMS Gradient Norm / a.u. | 0.00007670 | ||||||||
| Dipole Moment | 0.0008 | ||||||||
| Point Group | C1 | ||||||||
| Job CPU time | 9.0 seconds | ||||||||
| Imaginary frequency / cm-1 | -817.83 | ||||||||
| Item table | Item Value Threshold Converged?
Maximum Force 0.000077 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.001325 0.001800 YES
RMS Displacement 0.000396 0.001200 YES
Predicted change in Energy=-1.914263D-07
Optimization completed.
-- Stationary point found.
| ||||||||
The transition that was found using the method is shown to be correct by comparison with that found using the Hessian method. As for the Hessian method, the terminal C atoms were shown to be 2.02 Å and a C-C-C bond angle of 120.5° Furthermore, it can be seen that both methods resulted in very similar transition state structures. This is expected, since the aim of both methods is to locate the same transition state, albeit using a different method. In fact, the electronic energy and imaginary frequency were found to be essentially identical for the two methods as the same level of theory is used thus giving the same structure and energy.
The two methods are similar in that both require the use of a transition state. Where they differ is that the Hessian only works effectively when the guess structure shows strong resemblance with the actual transition state. Whereas, for the Frozen Coordinate method, the 'unfrozen' parts of the molecule is optimised before the transition state is found and optimised therefore, it is a better method when the structure of the transition state is unknown.
Boat transition state - QST2 Method
The Boat transition state was optimised using the QST2 method. The QST2 method predicts the structure of the transition state based on the optimised reactants and products. Therefore, the optimised anti2 conformer of 1,5-hexadiene generated in the previous step at the HF/3-21G level of theory was used. This is made possible by adjusting the numbering of the atoms to correpond to a Cope rearragement. This is shown below.
However, calculation using these reactants and products crashed. This is because rather than finding the boat transition state, the calculation found the chair transition structure but more dissociated. To solve this problem, the original input file was modified to render it more similar to the actual boat transition state. This if done by changing the dihedral angle of the four central carbon to 0° and the 2 central C-C-C bond angles to 100°.
The modified reactant and product was then set up for optimisation to a transition state and was successful illustrated below.
| Optimisation summary of boat transition state using QST2 method .log file | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Jmol File | 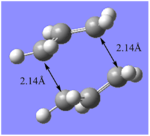 | ||||||||
| File Type | .log | ||||||||
| Calculation Type | FREQ | ||||||||
| Calculation Method | RHF | ||||||||
| Basis Set | 3-21G | ||||||||
| Charge | 0 | ||||||||
| Spin | Singlet | ||||||||
| Total Energy / a.u. | -231.60280200 | ||||||||
| RMS Gradient Norm / a.u. | 0.00007087 | ||||||||
| Dipole Moment | 0.1579 | ||||||||
| Point Group | Cs | ||||||||
| Job CPU time | 8.0 seconds | ||||||||
| Imaginary frequency / cm-1 | -839.94 | ||||||||
| Item table | Item Value Threshold Converged?
Maximum Force 0.000085 0.000450 YES
RMS Force 0.000029 0.000300 YES
Maximum Displacement 0.001502 0.001800 YES
RMS Displacement 0.000377 0.001200 YES
Predicted change in Energy=-3.292801D-07
Optimization completed.
-- Stationary point found.
| ||||||||
The resulting boat-like transition state had a separation of 2.14 Å which is slightly larger than its chair counterpart. This is likely due to to the increased steric interactions present in the boat conformation, between the H and C atoms. Furthermore, the reported imaginary frequency at 840 cm-1 is indicative of the correct boat transition state being found. This value is more negative than that for the chair state (-818cm-1), thus indicating the presence of stronger interactions at the boat.
IRC of Chair transition state
The Intrisic Reaction Coordinate (IRC) method allows the simulation of the minimum energy pathway from the transition state to its local energy minimum of the potential energy surface. This can be either a minimum corresponding to the reactants or the products. The calculation therefore can be used to predict which conformers are formed from which transition state and the corresponding energies. The previously HF/3-21G optimised chair transition state was used in the IRC calculation. The calculation direction was set for forwards only to find the product minimum, the force constant was set to calculate always and a maximum of 50 points were set along the IRC. The simulated IRC is shown below and shows the formation of the product via formation of a C-C bond from the transition state structure.
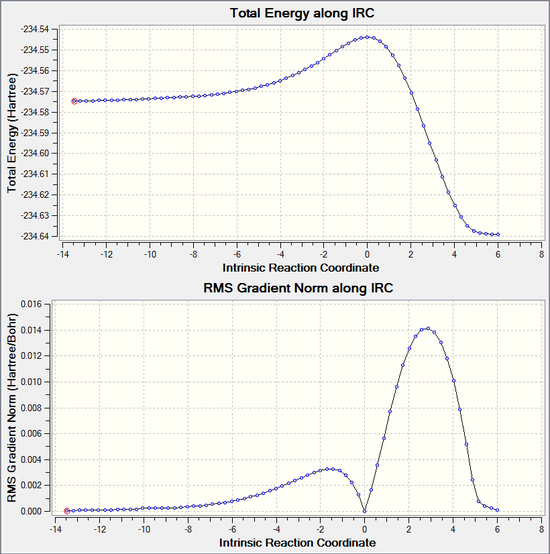
From observing the IRC simulated energy curve, it can be seen that after 44 steps, the calculation had reached what appears to be a minimum, which is illustrated by the RMS Gradient Norm curve plateauing at approximately 0.000 a.u. .
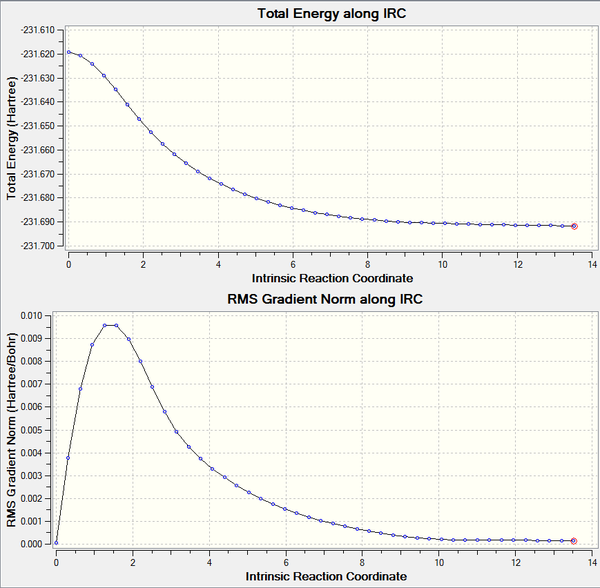
The product minimum found by the IRC simulation had an energy of -231.691577. From visualising the final structure in Gaussian, it can be observed that it bares close resemblance to the gauche2 conformer, although the energy is closer to that of the gauche4 conformer. This suggests that the minimum was not truly reached. Therefore, to ascertain the real minimum structure, the final point corresponding to the minimum structure found using the IRC was further optimised using the HF/3-21G method.
Optimisation of the final IRC structure, resulted in the gauche2 conformer being found. This is confirmed by comparing the optimised conformer energy, -231.691667 to that in Appendix 1 which indeed corresponds to gauche2 . Furthermore, on optimisation, the point group changed from C1 to C2, and again by comparing to the appendix table, C2 corresponds to the said conformer. It is also important to note that although the minimum structure found by the IRC was closer in energy to gauche4, on optimisation the gauche2 conformer was found. This may be due to less structural rearrangement required to form the gauche2 conformer.
Improvement 2, which involves increasing the number of steps in the calculation did not improve the result since the IRC simulation finds the minimum in 44 and thus terminates at this point. Likewise, Improvement 3 was also not a plausible improvement, since setting the calculate force constants setting to 'Always' was pre-defined in the step previous.
| Optimisation summary of last point of IRC simulation .log file | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Jmol File |  | ||||||||
| File Type | .log | ||||||||
| Calculation Type | FOPT | ||||||||
| Calculation Method | RHF | ||||||||
| Basis Set | 3-21G | ||||||||
| Charge | 0 | ||||||||
| Spin | Singlet | ||||||||
| Total Energy / a.u. | -231.69166702 | ||||||||
| RMS Gradient Norm / a.u. | 0.00000474 | ||||||||
| Dipole Moment / Debye | 0.3806 | ||||||||
| Point Group | C2 | ||||||||
| Job CPU time | 11.0 seconds | ||||||||
| Item table | Item Value Threshold Converged?
Maximum Force 0.000010 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000299 0.001800 YES
RMS Displacement 0.000091 0.001200 YES
Predicted change in Energy=-2.404269D-09
Optimization completed.
-- Stationary point found.
| ||||||||
Activation energies
In order to calculate the activation energies for the cope rearragement (i.e. the energy difference between the transition state maximum and the reactant minimum) via both transition states, both optimised transition states, chair and boat,were reoptimised using the B3LYP/6-31G* level of theory and a frequency analysis was conducted on both. The summaries are shown below.
| Optimisation summaries of Chair and Boat transition states at B3LYP/6-31G* level of theory | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Chair .log file | Boat .log file | ||||||||
| Jmol File | 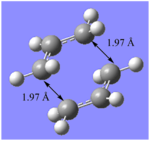 |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FREQ | FREQ | |||||||
| Calculation Method | RB3LYP | RB3LYP | |||||||
| Basis Set | 6-31G(d) | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | -234.55698303 | -234.54309307 | |||||||
| RMS Gradient Norm / a.u. | 0.00000268 | 0.00000193 | |||||||
| Dipole Moment | 0.0000 | 0.0613 | |||||||
| Point Group | C1 | Cs | |||||||
| Job CPU time | 2 mins 56.0 secs | 3 mins 6.7 secs | |||||||
| Item table | Item Value Threshold Converged?
Maximum Force 0.000007 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000056 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-4.270506D-10
Optimization completed.
-- Stationary point found.
|
Item Value Threshold Converged?
Maximum Force 0.000025 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.000318 0.001800 YES
RMS Displacement 0.000128 0.001200 YES
Predicted change in Energy=-8.152601D-09
Optimization completed.
-- Stationary point found.
| |||||||
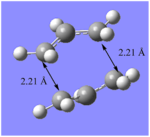
On re-optimisation of the transition states, using a different method, DFT and higher basis set 6-31G(d), separation to the terminal carbons of the allyl fragments changed. For the chair structure, the separation shortened from 2.02 Å to 1.97 Å and for the boat the separation increased from 2.14 Å to 2.21 Å.
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Structure | Electronic energy / a.u. | Sum of electronic and zero-point energies/ a.u. | Sum of electronic and thermal energies/ a.u | Electronic energy / a.u. | Sum of electronic and zero-point energies/ a.u. | Sum of electronic and thermal energies/ a.u |
| at 0K | at 298.15K | at 0K | at 298.15K | |||
| Chair TS | -231.619322 | -231.466696 | -231.461338 | -234.556983 | -234.414929 | -234.409008 |
| Boat TS | -231.602802 | -231.450928 | -231.445299 | -234.543093 | -234.402343 | -234.396008 |
| Anti2 conformer reactant | -231.692535 | -234.539539 | -231.532564 | -234.611703 | -234.469212 | -234.461856 |
The table below shows the activation energies data derived from the sum of electronic and zero-point energies at 0K and sum of electronic and thermal energies at 298.15K above.
Upon heating of the system from T = 0 K to T = 298 K the activation energy for both the chair and boat pathways decreases. An explanation for this occurrence is that the reactant has a greater number of accessible vibrational modes than the transition state, thus its potential energy increases comparatively more upon heating. This reduces the energy gap between the reactant and transition state, thus a lower activation energy.
The data also suggests that the B3LYP/6-31G* level of theory correlates much better with the experimental values. This is expected since the DFT method uses a larger basis set, resulting in better results.
The relative activation energies clearly illustrates that the cope rearrangement will preferably proceed through the lower energy chair transition state. This is the case because the rearrangemeant reaction generates the same product despite the transition state which the reaction proceeds through. Therefore, within an energy argument, the chair transition state is favoured as it is the lowest energy pathway.
| HF/3-21G | B3LYP/6-31G* | Expt. [3] | |||
|---|---|---|---|---|---|
| Temperature | at 0K | at 298.15K | at 0K | at 298.15K | at 0K |
| ΔE(Chair) / kcalmol-1 | 45.71 | 44.69 | 34.06 | 33.16 | 33.5 ± 0.5 |
| ΔE(Boat) / kcalmol-1 | 55.60 | 54.76 | 41.96 | 41.32 | 44.7 ± 2.0 |
Diels Alder Cycloaddition
The Diels Alder reaction belongs to a class of reactions known as pericyclic reactions. The Diels alder reaction is specifically [4+2] cycloaddition between a conjugated diene and an alkene molecule, also called the dienophile, to form a substituted cyclohexene system. The reaction is an example of a concerted pericyclic reaction and proceeds through a single cyclic transition state. This means that the reaction is governed by the symmetry of orbitals involved and more specfically it proceeds via the suprafacial/suprafacial interaction of a 4π electron system with a 2π electron system, an interaction that is thermally allowed as a 4n+2 cycloaddition based on the Huckel-Mobius theory.[4]
The π orbitals of the dieneophile overlaps with the π orbitals of the diene to form two new σ C-C bonds. In general, the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. However, the reaction is only possible when there is significant overlap density between the orbitals and the orbitals must have the same symmetry properties in order to do overlap.
Reaction between cis-butadiene and ethylene
In this part of the assignment, we will optimise the starting materials, cis-butadiene and ethylene before considering the HOMO and LUMO of each reactant to study how the molecules come together to react to form the product cyclohexene in the diels alder cycloaddition. We will also examine the Transition State geometry through which the reaction proceeds to further understand the nature of the reaction pathway.

Optimisation of reactants
Cis-butadiene
Cis-butadiene was firstly optimised using the AM1 semi-empirical molecular orbital method. The optimised structure had C=C bond lengths of 1.33 Å and C-C bond length of 1.45 Å, and an optimised C=C-C bond angle of 125.7°. The optimisation was checked to have been succesfully by convergence of the set of forces and displacements, as well as a low RMS Gradient Norm value. In comparison, on optimisation of the molcule using the B3LYP/6-31G* method and basis set the C-C and C-C bond lengths changed to 1.34 Å and 1.47 Å respectively, and the C=C-C bond angle increased to 127.3°. This shows that using a higher level of theory results in structural properties closer to literature value (Typical C=C double bond length 1.34 Å. and typical C-C double bond length is 1.54 Å.[5]) Further to this, the C-C bond length shows greatest discrepancy to a typical C-C bond length due to the partial double bond character it has in the molecule, which shortens and strengthens the bond.
| Optimisation summary of Cis-butadiene | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Semi empirical AM1 .log file | B3LYP/6-31G* .log file | |||||||
| Jmol File |  |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FOPT | FOPT | |||||||
| Calculation Method | RAM1 | RB3LYP | |||||||
| Basis Set | ZDO | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | 0.04879718 | -155.985956 | |||||||
| RMS Gradient Norm / a.u. | 0.00001429 | 0.00001967 | |||||||
| Dipole Moment / Debye | 0.0414 | 0.0852 | |||||||
| Point Group | Cs | Cs | |||||||
| Job CPU time | 20.0 seconds | 31.0 seconds | |||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000025 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000318 0.001800 YES RMS Displacement 0.000128 0.001200 YES Predicted change in Energy=-8.152601D-09 Optimization completed. -- Stationary point found. |
Item Value Threshold Converged? Maximum Force 0.000032 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.000242 0.001800 YES RMS Displacement 0.000080 0.001200 YES Predicted change in Energy=-1.405001D-08 Optimization completed. | |||||||
The HOMO and LUMO of cis-butadiene which are involved in the diels-alder reaction was reported and shown below. The MOs are important to understanding the reactivity and how the molecules come together to bond. The molecules are derived from the B3LYP/6-31G* level of theory. From the visualisation of the MOs it can be seen that the HOMO contains 1 node and the LUMO contains 2 nodes, which is consistent which the fact that the HOMO is lower energy than the LUMO.
| MO | HOMO | LUMO |
|---|---|---|
| Visualisation | 
|
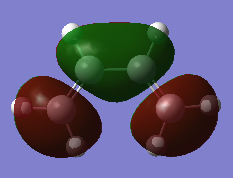
|
| Symmetry with respect to plane | Asymmetric | Symmetric |
Ethene
As in the case cis-butadiene, ethene was firstly optimised using the AM1 semi-empirical molecular orbital method followed by optimisation using the higher level of theory, B3LYP/6-31G*. The optimsed C=C bond has a bond length of 1.33 Å in both cases, suggesting that for very simple molecules, the two levels of theory give similar results despite using different approximations and calculation methods. This optimisation summaries are shown below.
| Optimisation summary of Ethene | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | Semi-empirical AM1 .log file | B3LYP 6-31G(d) .log file | |||||||
| Jmol File |  |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FOPT | FOPT | |||||||
| Calculation Method | RAM1 | RB3LYP | |||||||
| Basis Set | ZDO | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | 0.02619027 | -78.587458 | |||||||
| RMS Gradient Norm / a.u. | 0.00003328 | 0.00005397 | |||||||
| Dipole Moment / Debye | 0.0000 | 0.0000 | |||||||
| Point Group | C2h | C2h | |||||||
| Job CPU time | 15.0 seconds | 14.0 seconds | |||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000162 0.000450 YES RMS Force 0.000049 0.000300 YES Maximum Displacement 0.000414 0.001800 YES RMS Displacement 0.000220 0.001200 YES Predicted change in Energy=-3.787282D-08 Optimization completed. -- Stationary point found. |
Item Value Threshold Converged?
Maximum Force 0.000104 0.000450 YES
RMS Force 0.000038 0.000300 YES
Maximum Displacement 0.000169 0.001800 YES
RMS Displacement 0.000092 0.001200 YES
Predicted change in Energy=-2.420379D-08
Optimization completed.
-- Stationary point found.
| |||||||
The HOMO and LUMO of Ethene are symmetric and asymmetric with respect to the plane respectively. This means the HOMO and LUMO of cis-butadiene and ethene have complimentary symmetries, therefore, the rule for the HOMO and LUMO of reacting molecules having the same symmetry property is fulfilled (i.e the HOMO of cis-butadiene can overlap with the LUMO of ethene, and the LUMO of cis-butadiene can overlap with the HOMO of ethene).
| MO | HOMO | LUMO |
|---|---|---|
| Visualisation | 
|
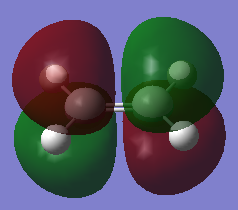
|
| Symmetry with respect to plane | Symmetric | Asymmetric |
Transition state
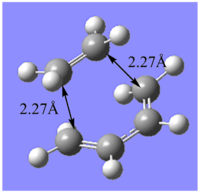
The transition state for the Diel-Alder cycloaddtion of cis-butadiene and ethene was first calculated at the semi-empirical AM1 level of theory before using a higher level of theory, namely B3LYP/6-31G*, to obtain a more accurate structure and energy. The biocyclo[2.2.2]octane fragment as the template in forming the guess structure. The bridging ethylene group was removed and the 2 C-C bonds equivalent to those that form in the reaction were lengthened to a separation of ~2.20 Å . The Hessian method was employed to optimise the structure with the same procedure as used previously in the optimisation of the cope rearrangement chair transition state. The optimisation summary using both levels of theory is shown below.
| Optimisation summaries of Diels Alder transition state of cis-butadiene and ethene using AM1 method and DFT method method | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Semi-empirical AM1 method .log file | B3LYP/6-31G* | ||||||||
| Jmol File | 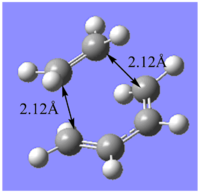 |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FREQ | FREQ | |||||||
| Calculation Method | RAM1 | RB3LYP | |||||||
| Basis Set | ZDO | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | 0.11165467 | -234.54389654 | |||||||
| RMS Gradient Norm / a.u. | 0.00001068 | 0.00000410 | |||||||
| Dipole Moment | 0.5605 | 0.3942 | |||||||
| Point Group | C1 | C1 | |||||||
| Job CPU time | 5.0 secs | 1 min 28.0 secs | |||||||
| Imaginary frequency / cm-1 | -956.20 | -525.07 | |||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000035 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.001451 0.001800 YES RMS Displacement 0.000417 0.001200 YES Predicted change in Energy=-2.369046D-08 Optimization completed. -- Stationary point found. |
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000362 0.001800 YES RMS Displacement 0.000115 0.001200 YES Predicted change in Energy=-8.782177D-09 Optimization completed. -- Stationary point found. | |||||||
The results of the optimisation firstly indicates that by improving the level of theory and method used from the semi-empirical AM1 method to the B3LYP/6-31G* method, the structure of the transition state changes. Particularly, the C-C separation between the terminal C carbons of the reacting fragments changes from 2.12Å to a length of 2.27 Å which matches the value found in literature. Since, the van der Waals radius of a Carbon atom is 1.70 Å and the partially formed σ-bonds are 2.27 Å apart, they are longer than the typical C-C bond length but shorter than the sum of the can der Waals radii of the 2 carbon atoms. Therefore, this indicates an overlap of electron density between the MOs involved in bonding and correpsonds to the fragments coming together in a bonding type interaction. This is shown in the animation below. The symmetric movement of the 2 fragments towards each other is indicative of the synchronised formation of the 2 C-C σ bonds. There is also a vibration reported at frequency 135.80 cm-1 and involves twisting of the ethyene fragment corresponding to a asynchronous vibration of the transition state. Since this vibration has a positive frequency value it does not correspond to the forward reaction, rather it is a vibration characteristic of the transition state itself.
Furthermore, in the transition state structure, it can be seen that in the B3LYP/6-31G* case, all the original C=C double bonds in the original fragments now have a length of 1.38 Å and the original C-C single bond of the butadiene has a bond length of 1.40 Å. This indicates that the double bonds have partially lost their double bond (c.f. a typical C=C double bond length is 1.34 Å.[5]) character and lengthened towards the single C-C bond (c.f. a typical C-C double bond length is 1.54 Å [5].)length in the product. Therefore, in the transition state the bonds are neither formal C-C or C=C bonds, but an intermediate.
 |
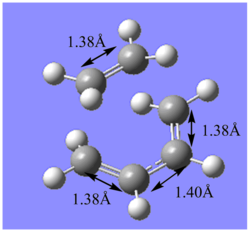 |
The MOs of the transition state are depicted below.
| MO | HOMO-1 | HOMO | LUMO |
|---|---|---|---|
| B3LYP/6-31G* | 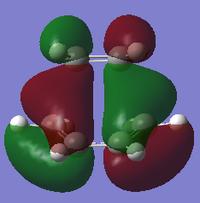
|
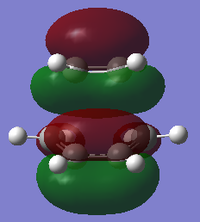
|
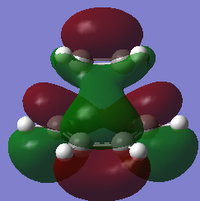
|
| Symmetry with respect to plane | Asymmetric | Symmetric | Asymmetric |
| Semi-empirical AM1 | 
|
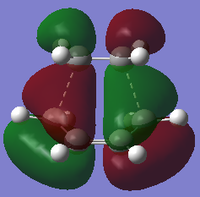
|
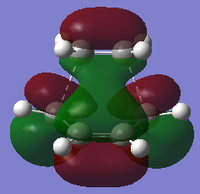
|
| Symmetry with respect to plane | Symmetric | Asymmetric | Asymmetric |
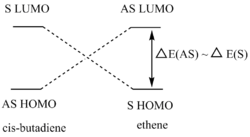
Using the B3LYP/6-31G* level of theory, the HOMO of transition state structure can be seen to by symmetric and thus is formed from the combination of the symmetric MOs of cis-butadiene and ethene. More specifically, the interaction involves the ethene HOMO and the cis-butadiene LUMO. Since both orbitals are symmetric in property, there is significant overlap density rendering the reaction possible. Furthermore, on examination of the transition state orbitals using the AM1 level of theory, the HOMO is now asymmetric and the HOMO-1 is symmetric. This is clearly the reverse of the B3LYP/6-31G* case which suggests that using 2 different calculation methods will yield different results as a result of different approximations, assumptions and calculation used by the two methods. More importantly to note is that the HOMO and HOMO-1 molecular orbitals have switched places and energies between the two methods because they are both very similar in energy. This is due to the energy difference between the highest occupied asymmetric MO being close in energy to the highest occupied symmetric MO in the 2 reactant molecules, making a re-ordering of the different modes possible. This is shown schematically on the right.
Calculation of activation energies
The activation energies of the diels alder reaction was calculated using the 'Sum of electronic and zero-point energies' and 'Sum of electronic and thermal energies'. The table below shows the associated data for each method used in the optimisation and frequency analysis process.
| Semi-empirical AM1 | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Structure | Electronic energy / a.u. | Sum of electronic and zero-point energies/ a.u. | Sum of electronic and thermal energies/ a.u | Electronic energy / a.u. | Sum of electronic and zero-point energies/ a.u. | Sum of electronic and thermal energies/ a.u |
| at 0K | at 298.15K | at 0K | at 298.15K | |||
| Diels Alder TS | 0.111655 | 0.253275 | 0.259453 | -234.543897 | -234.403324 | -234.396906 |
| cis-butadiene reactant | 0.048797 | 0.134553 | 0.138573 | -155.985956 | -155.900816 | -155.896777 |
| ethene reactant | 0.026190 | 0.077198 | 0.080252 | -78.597458 | -78.536232 | -78.533191 |
The table below shows the activation energies data derived from the sum of electronic and zero-point energies at 0K and sum of electronic and thermal energies at 298.15K above.
Upon heating of the system from T = 0 K to T = 298 K the activation energy of the reaction decreases. An explanation for this occurrence is that the reactant has a greater number of accessible vibrational modes than the transition state, thus its potential energy increases comparatively more upon heating. This reduces the energy gap between the reactant and transition state, thus a lower activation energy.
The data also suggests that the Semi-empirical AM1 method correlates much better with the experimental values. This is an unexpected since a higher level of theory should give results closer to experimental value. It may be that the experimental value is incorrect since it was extrapolated from energies which were measured at much higher temperatures.
| AM1 | B3LYP/6-31G* | Expt. [6] | |||
|---|---|---|---|---|---|
| Temperature | at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K |
| ΔE(Diels Alder TS) / kcalmol-1 | 26.06 | 25.49 | 21.16 | 20.75 | 25.1 |
IRC
An IRC simualtion was also ran for the diels-alder cycloaddtion reaction involving cis-butadiene and ethene. The calcultion was ran both in the forwards and backwards reaction together in one calculation which involves following the minimum energy path from the transition structure down both sides of the transition state maximum to its local minima on a potential energy surface. The calculation was set up to using a maxmimum of 100 steps, although the calcualtion found both minima after 69 steps. This finds the reactant minimum and also the product minimum. The graphical representation is shown below. It can be interpreted from the graph that, from the maximum of the transition state, the calculation follows the minimum energy pathway in the backwards direction to find the reactants, and then in the forwards reaction to find the products. The product minimum is found when the RMS Gradient Norm value reaches 0.000 a.u., indicating a stationary point.
Reaction between Maleic Anhydride and Cyclohexa-1,3-diene
A complex case of the Diels Alder reaction was also studied and this involved the reaction between Maleic anhydride and cyclohexa-1,3-diene. This is a more complex system than the cis-butadiene and ethene case studied in the last step since both the diene and the dienophile are substituted and especially in the case of the maleic anhydride dienophile, which contains O atoms with π orbitals which can interact with the double bond that is being formed in the product. With this in mind, stereoisomeric products are thus possible depending on whether in the transition state the O π orbitals are directly above or below the diene fragment to form the endo product, or pointing away to form the exo product.

Optimisation of reactants
Cyclohexa-1,3-diene
Cyclohexa-1,3-diene was first optimised using the semi-empirical AM1 method before further optimisation using a high level of theory to get a better result. From the AM1 optimisation method, it can be seen that the optimised molecule does not correspond to an energy minimum since at the sp3 C atoms, the H atoms are eclipsed, therefore suffering from electrostatic repulsion and torsional strain about the sp3 C-C bond. After optimisation at the B3LYP/6-31G* level of theory, the optimised molcule is relieved of this torsional strain by the H atoms being in the gauche position. Thus the optimised strucutre at a higher level is more likely to be the energy minimum. The optimisation summaries are shown below.
| Optimisation summaries of Cyclohexa-1,3-diene using AM1 theory and B3LYP/6-31G* thoery. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Semi empirical AM1 method .log file | B3LYP/6-31G* .log file | ||||||||
| Jmol File |  |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FREQ | FREQ | |||||||
| Calculation Method | RAM1 | RB3LYP | |||||||
| Basis Set | ZDO | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | 0.02771129 | -233.418932 | |||||||
| RMS Gradient Norm / a.u. | 0.00000562 | 0.00000914 | |||||||
| Dipole Moment | 0.4313 | 0.3780 | |||||||
| Point Group | C2 | C2 | |||||||
| Job CPU time | 5.0 secs | 47 secs | |||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000249 0.000450 YES RMS Force 0.000046 0.000300 YES Maximum Displacement 0.001515 0.001800 YES RMS Displacement 0.000409 0.001200 YES Predicted change in Energy=-3.537068D-07 Optimization completed. -- Stationary point found. |
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000022 0.001200 YES
Predicted change in Energy=-2.874539D-09
Optimization completed.
-- Stationary point found.
| |||||||
The HOMO and LUMO of diene was also found and illustrated below.
| MO | HOMO | LUMO |
|---|---|---|
| Visualisation | 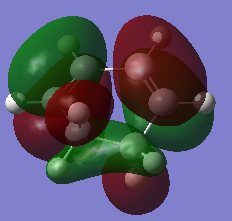
|
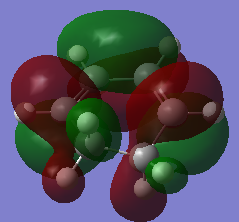
|
| Symmetry with respect to plane | Symmetric | Asymmetric |
Maleic Anhydride
Maleic Anhydride is an electron deficient dienophile since the O atoms withdraws electron density from the C=C double bond thereby lowering the energy of the LUMO thus making it a better acceptor. As with Cyclohexa-1,3-diene, Maleic Anhydride was optimised first using AM1 and improved upon using the DFT method.
| Optimisation summaries of Maleic Anhydride using AM1 theory and B3LYP/6-31G* thoery. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Semi empirical AM1 method .log file | B3LYP/6-31G* .log file | ||||||||
| Jmol File |  |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FOPT | FREQ | |||||||
| Calculation Method | RAM1 | RB3LYP | |||||||
| Basis Set | ZDO | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | -0.12182419 | -379.289544 | |||||||
| RMS Gradient Norm / a.u. | 0.00003135 | 0.00008349 | |||||||
| Dipole Moment | 4.5763 | 4.0715 | |||||||
| Point Group | C1 | C1 | |||||||
| Job CPU time | 28.0 secs | 45.0 secs | |||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000037 0.000450 YES RMS Force 0.000019 0.000300 YES Maximum Displacement 0.001162 0.001800 YES RMS Displacement 0.000389 0.001200 YES Predicted change in Energy=-6.120569D-08 Optimization completed. -- Stationary point found. |
Item Value Threshold Converged?
Maximum Force 0.000075 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.001200 0.001800 YES
RMS Displacement 0.000287 0.001200 YES
Predicted change in Energy=-3.608036D-07
Optimization completed.
-- Stationary point found.
| |||||||
The HOMO and LUMO of the dienophile was also found and illustrated below. As before, these will be used in understanding of the reaction and how the molecules interact to come together to form the transition state. The HOMO is Asymmetric and the LUMO Symmetric with respect to the plane. This is complementary to the case of cyclohexa-1,3-diene and thus allows for good overlap between the frontier orbitals of the reactants in the transition state. As a result it facilitates the reaction.
| MO | HOMO | LUMO |
|---|---|---|
| Visualisation | 
|

|
| Symmetry with respect to plane | Asymmetric | Symmetric |
Transition state
Both the exo and the endo transition state structures were located using the AM1 method and the B3LYP/6-31G* method and basis set. As with the previous Diels Alder calculation, the Hessian method was chosen. The optimisation was set to TS(Berny) and force constants calculated Once, along with the keywords opt=noeigen to optimise the reactants to a transition state. Again, since using the Hessian method requires the guess structure to closely resemble the actual transition state, the bicyclooctane fragment was used as a starting template and the distance between the reactants was set to ~2.20 Å apart. However, in contrast to the previous example, to transition state structures had to be constructed and optimised. The introduction of the electron-withdrawing substituents on the dienophile renders it possible to make 2 stereoisomers, Endo and Exo.
The Endo transition state was generated by positioning the O=C π orbitals directly above or below the diene fragment and the Exo counterpart was formed by positiioning the the C=O bonds away. This is shown below along with the optimisation summaries.
| Optimisation summaries of Endo and Exo transition state. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Transition state | Endo | Exo | |||||||
| Method | Semi-empirical AM1 method .log file | B3LYP/6-31G* method .log file | Semi-empirical AM1 method .log file | B3LYP/6-31G* method .log file | |||||
| Jmol File |  |
 | |||||||
| File Type | .log | .log | .log | .log | |||||
| Calculation Type | FREQ | FREQ | FREQ | FREQ | |||||
| Calculation Method | RAM1 | RB3LYP | RAM1 | RB3LYP | |||||
| Basis Set | ZDO | 6-31G(d) | ZDO | 6-31G(d) | |||||
| Charge | 0 | 0 | 0 | 0 | |||||
| Spin | Singlet | Singlet | Singlet | Singlet | |||||
| Total Energy / a.u. | -0.051505 | -612.683397 | -0.050420 | -612.679311 | |||||
| RMS Gradient Norm / a.u. | 0.00001305 | 0.00000710 | 0.00000420 | 0.00000453 | |||||
| Dipole Moment | 6.1665 | 6.1140 | 5.5638 | 5.5502 | |||||
| Point Group | C1 | C1 | C1 | C1 | |||||
| Job CPU time | 11.5 secs | 9 mins 43.0 secs | 11.4 secs | 31 mins 40.2 secs | |||||
Furthermore, all optimisation calculations were shown to have been successful by a low RMS Gradient Norm value and convergence of all forces and displacements in each case.
| Item table | ||||
|---|---|---|---|---|
| Endo | AM1 | Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000776 0.001800 YES
RMS Displacement 0.000160 0.001200 YES
Predicted change in Energy=-1.005596D-09
Optimization completed.
-- Stationary point found.
|
| ||
| B3LYP/6-31G* | Item Value Threshold Converged? Maximum Force 0.000249 0.000450 YES RMS Force 0.000046 0.000300 YES Maximum Displacement 0.001515 0.001800 YES RMS Displacement 0.000409 0.001200 YES Predicted change in Energy=-3.537068D-07 Optimization completed. -- Stationary point found. | |||
| Exo | AM1 | Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000226 0.001800 YES RMS Displacement 0.000055 0.001200 YES Predicted change in Energy=-3.116172D-09 Optimization completed. | | ||
| B3LYP/6-31G* | Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000022 0.001200 YES
Predicted change in Energy=-2.874539D-09
Optimization completed.
-- Stationary point found.
| |||
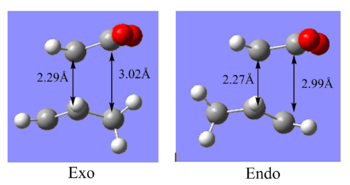
The first thing to notice from the summaries of the two transition states is that the endo is lower energy than exo, by an amount of 2.56 kcal/mol. Since the diels alder reaction proceeds under kinetic control, it is the endo transition state through which the reaction proceeds. It can also be noticed that the distance between the C atoms that form the new C-C bonds, are 2.27 Å and 2.29 Å in the endo and exo transition state respectively. The separation between the carbonyl C of the dienophile and its nearest C atom in the diene is similarly longer in the exo case than the endo. In the exo case, this separation is ~3.02 Å and 2.99 Å in the endo case. Evaluating this leads to explanation that the exo structure is more sterically crowded than the endo structure and this steric strain contributes to the higher energy of the exo state. This point is further reinforced by the fact that the H atoms of the sp3 C atoms are much closer to the -(C=O)-O-(C=O)- fragment of the maleic anhydride in the exo form which can be illustrated in the diagram to the right. However, overall the distances can be argued to be relatively similar suggesting that there may be an optimum distance for orbital overlap.
In addition to the unfavourable steric environment, the endo form is also rendered lower energy hence more stable than the exo form by the secondary orbital overlaps that are present in the transition state. This secondary orbital stabilisation is only possible in the endo structure as it requires the correct alignment of the π/π* orbitals of the O atoms in the maleic anyhride fragment and the diene fragment in cyclohexa-1,3-diene. On the other hand, in the exo structure the -(C=O)-O-(C=O)- fragment is orientated in the opoosite direction thus it is too far away in space to effectively overlap with the orbitals of the diene. The animation from the frequency analysis of both transition states is shown below. In both cases, the synchronous bond formation can be seen.
| Transition state | Endo | Exo |
|---|---|---|
| Visualisation | 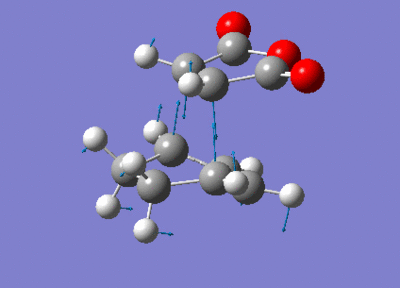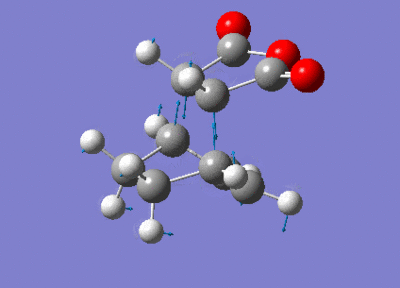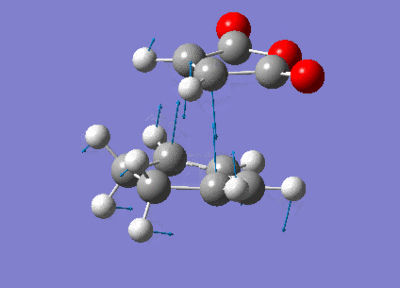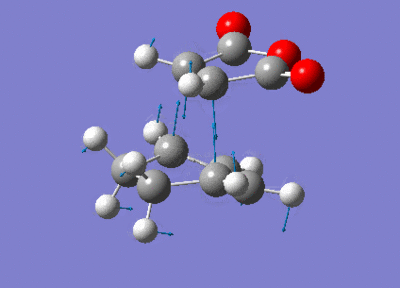 |
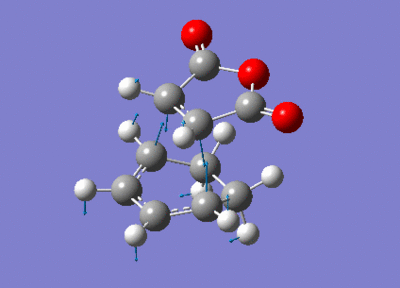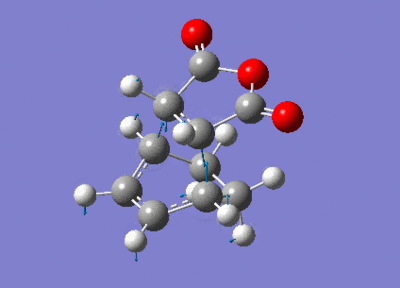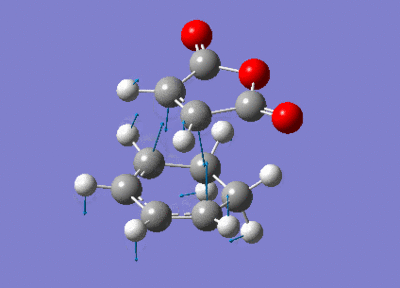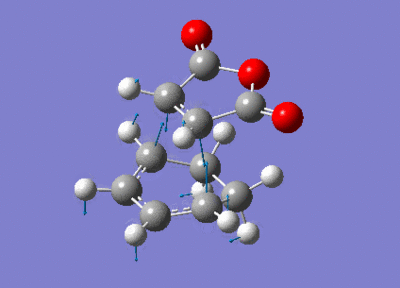 |
| Imaginary frequency / cm-1 | -446.95 | -448.47 |
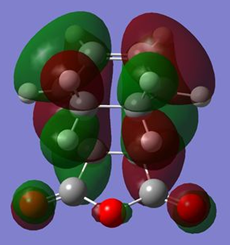
The HOMOs of both transition states are illustrated below.
| MO | HOMO | |
|---|---|---|
| Transition state | Endo | Exo |
| Visualisation | 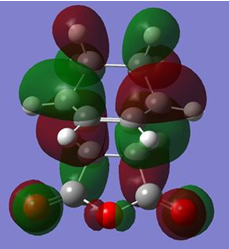
|
|
| Symmetry with respect to plane | Asymmetric | Asymmetric |
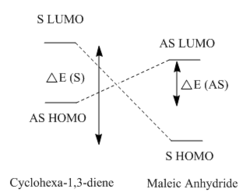
The reason that the HOMOs are asymmetric in symmetry is because the constituent HOMO of cyclohexa-1,3-diene and LUMO of the maleic anhydride are both asymmetric. Furthermore, unlike the case for cis-butadiene and ethene, the energy difference between the set of asymmetric orbitals is much lower than the energy difference between the symmetric set (i.e. HOMO of maleic anhydride and LUMO of cyclohexa-1,3-diene). This is the case because the electron withdrawing anhydride fragment renders its HOMO and LUMO to be lower in energy thus allowing better primary orbital overlap between the diene HOMO and dienophile LUMO. As a result, this favours the formation of the HOMO from the asymmetric constituent MOs. This is shown schematically on the right.
Activation energies
The activation energies for the reaction between maleic anhydride and cyclohexa-1,3-diene was calculated using the process employed in previous sections.
| Semi-empirical AM1 | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Structure | Electronic energy / a.u. | Sum of electronic and zero-point energies/ a.u. | Sum of electronic and thermal energies/ a.u | Electronic energy / a.u. | Sum of electronic and zero-point energies/ a.u. | Sum of electronic and thermal energies/ a.u |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Endo TS | -0.051505 | 0.133495 | 0.143683 | -612.683397 | -612.502141 | -612.491787 |
| Exo TS | -0.050420 | 0.134880 | 0.144881 | -612.679311 | -612.498013 | -612.488662 |
| Maleic anhydride reactant | -0.121824 | -0.063345 | -0.058192 | -379.289544 | -379.233656 | -379.228472 |
| Cyclohexa-1,3-diene reactant | 0.027711 | 0.152502 | 0.157726 | -233.418932 | -233.296104 | -233.290931 |
The table below shows the activation energies data derived from the sum of electronic and zero-point energies at 0K and sum of electronic and thermal energies at 298.15K above.
It can be noticed from the table that as expected the activation energy to the endo transition state requires lower enery. However, the required energy difference between the exo and endo transition states appear very small in both cases using different methods. Furthermore, on heating, the activation energies decease as expected. As before this may be explained by the greater number of accessible vibrational modes of the reactants compared to the transition state, thus its potential energy increases comparatively more upon heating. This reduces the energy gap between the reactant and transition state, thus a lower activation energy. Moreover, the transition energy difference between the endo and exo state is larger when the higher level of theory is used.
| HF/3-21G | B3LYP/6-31G* | |||
|---|---|---|---|---|
| Temperature | at 0 K | at 298.15 K | at 0 K | at 298.15 K |
| ΔE(Endo) / kcalmol-1 | 27.82 | 27.70 | 17.33 | 17.33 |
| ΔE(Exo) / kcalmol-1 | 28.69 | 28.46 | 19.92 | 19.29 |
IRC
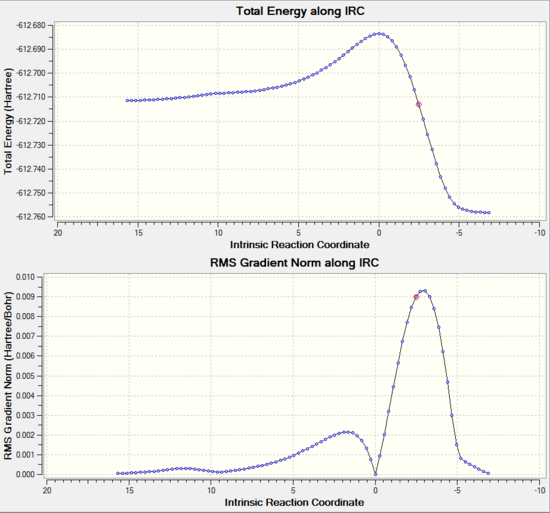
An IRC simulation was also ran for both endo and exo transition states. The calcultion was ran both in the forwards and backwards reaction together in one calculation which involves following the minimum energy path from the transition structure down both sides of the transition state maximum to its local minima on a potential energy surface. The IRCs will differ slightly since the energy of the transition states are different due to the different steric environments and secondary orbital stabilising interactions in the two transition states. The calculation was set up to using a maxmimum of 100 steps, but terminated after 90 steps for the exo state and 83 for the endo. Furthermore, the calculation was ran in both directions so to find the reactant minimum and also the product minimum. The graphical representations are shown below.
Endo transition state
 |
 |
Exo transition state
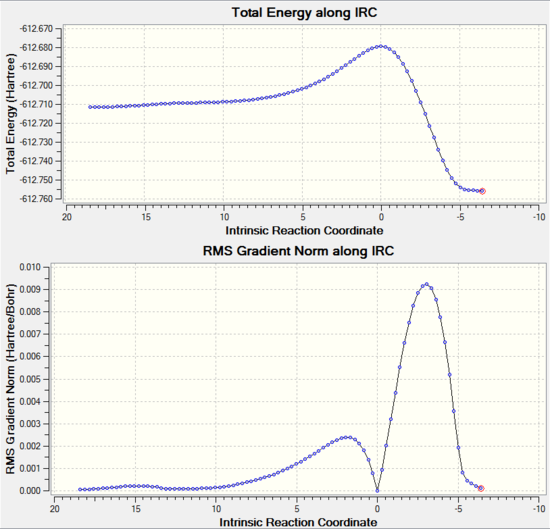 |
 |
The IRC clearly shows that as calculated before the Endo transition state is lower in energy. From visual interpretation of the graph, it appears that the optimum endo and exo products have been reached since the RMS Gradient Norm value has reached 0.000 a.u., indicating that the rate of change of energy of the molecule has become constant corresponding to an energy minima. However, to ensure the optimised products were found, the last point of the IRC corresponding to the final product structure found was optimised using the B3LYP/6-31G* method and basis set. The optimisation summaries are shown below along with the item table showing that the optimisation was succesfully based on convergence of the forces and displacements.
The reported final energy of the endo product is lower in energy than the exo product; -612.758290 a.u. and -612.755785 a.u. respectively. These are as expected lower energy than the transition states and also the sum of the energy of the reactant materials. The difference in energy of the final products may be attributed to the fact that anhydride fragments are orientated in different directions. The exo is lower in energy because the anhydride fragment is directed upwards towards the -CH2CH2- bridgehead of the molecule. Specifically, the distance between the C atoms -(C=O)-O-(C=O)- fragment and the H atoms of the bridgehead is 2.63 Å of the resulting in much stronger unfavourable steric interactions. Since the endo product is lower in energy than the exo, it is not only the kinetic product but also the thermodynamically favoured product.
| Optimisation summaries of Endo and Exo final product structures. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Endo .log file | Exo .log file | ||||||||
| Jmol File |  |
 | |||||||
| File Type | .log | .log | |||||||
| Calculation Type | FOPT | FOPT | |||||||
| Calculation Method | RB3LYP | RB3LYP | |||||||
| Basis Set | 6-31G(d) | 6-31G(d) | |||||||
| Charge | 0 | 0 | |||||||
| Spin | Singlet | Singlet | |||||||
| Total Energy / a.u. | -612.758290 | -612.755785 | |||||||
| RMS Gradient Norm / a.u. | 0.00001493 | 0.00001919 | |||||||
| Dipole Moment | 5.0200 | 4.7598 | |||||||
| Point Group | C1 | C1 | |||||||
| Job CPU time | 14 mins 14.9 secs | 14 mins 22.8 secs | |||||||
| Item table | Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000282 0.001800 YES RMS Displacement 0.000061 0.001200 YES Predicted change in Energy=-1.814164D-08 Optimization completed. |
Item Value Threshold Converged? Maximum Force 0.000050 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000443 0.001800 YES RMS Displacement 0.000104 0.001200 YES Predicted change in Energy=-3.024177D-08 Optimization completed. | |||||||
Solvent effects on the transition states
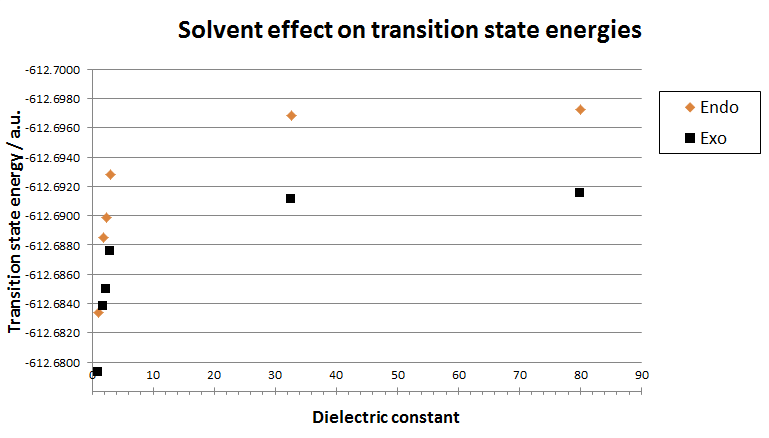
Further calculations were done to study the effect of different solvents, polar and apolar, on both the endo and exo transition states. This was done in Gausssian using the solvation function when running a calculation. The solvents used in the study were picked based on varying diaelectric constants to give a more thorough understanding of the effects. The solvents chosen in this simulation includes, methanol, diethyl ether, heptane, toluene and water. The results were plotted along with the the transition state energies calculated earlier which correspond to no solvent used, thus a gas phase reaction. The results are shown below.
| Transition state energies | |||
|---|---|---|---|
| Solvent | Dielectric constant | Endo / a.u. | Exo / a.u. |
| None (Gas phase) | 1 | -612.683397 | -612.679311 |
| Heptane | 1.92 | -612.688484 | -612.683760 |
| Toluene | 2.38 | -612.689870 | -612.684979 |
| Diethyl ether | 3.10 | -612.692782 | -612.687547 |
| Methanol | 32.7 | -612.696824 | -612.691130 |
| Water | 80.1 | -612.697231 | -612.691492 |
It can be derived from the graph that as the solvent becomes more polar (i.e. the dielectric constant increases), the transition state for both exo and endo becomes energetically more stable. This is because the polar solvent molecules are more able to stabilise the build up of charge in the transition state by spreading this charge over a larger area. As expected, the endo energy is lower than the corresponding exo energy since the endo transition state is more stabilised by secondary orbital interatctions as discussed previously. Furthermore, it can be seen in both cases that the transition energy plateaus towards a specfic energy value as the dieletric constant increase. This may be the maximum solvation effect that can be provided by the solvent. Since water, is about the most polar solvent as possible, this minimum energy of the solvatedtransition state may be close to the energy values given by the solvent water.
Conclusion
This computational assignment set out to study the reactants and transition states of the two reaction types: Cope rearrangement and Diels Alder cycloaddition. Calculations involved the optimisation and frequency analysis of the reactants and transition states using Gaussview and Gaussian.
The study of the Cope rearrangement was carried out specifically on 1,5-hexadiene. The various conformers of the reactant was briefly studied to find that generally the anti conformers where the middle four C atoms are in an anti-periplanar are more stable, which was explained by the maximum overlap of σ/σ* orbitals that are possible in this conformation. A surprising finding in this section was that the Gauche3 conformer was the most stable which may be attributed to the VdW attractive interaction between the terminal alkene groups. Thereafter, the chair and boat transition states of the reaction was studied to find that the chair transition state was favoured. This was done using several optimisation techniques including the Hessian method, Frozen Coordinate Method and QST2 for the boat transition state.
In the study of the Diels Alder reaction, we first encountered the reaction between cis-butadiene and ethene. Through optimisation of the reactants using the Semi-empirical AM1 method and DFT method and B3LYP/6-31G* basis set, we discovered that the latter method produced structural results that were more in line with literature. Next, by considering the energies associated with the transition state and reactants, the activation energies found using the DFT method more closely resembled experimental result.
We then carried out further study on the Diels Alder reaction using more complex reactants, Cyclohexa-1,3-diene and Maleic Anhydride. The results show that the Endo transition state is favoured due to secondary orbital interactions as well as having less steric interactions in the transition state compared to the Exo form. Although satisfactory results were obtained, the solvent effects were neglected in this reaction because realistically, reactions are always carried out in solvent to appropriately facilitate the reaction. In light of this, we performed a brief solvent investigation and found that the transition state is increasingly stabilised by more polar solvents. A more thorough understanding of solvation effects and the effect of specific interactions can be gained by investigating point interactions such as those between water molcules and the reactants and transition state. This would offer greater insight into the reactivity of the reaction.
Another improvement to be made in studying the reactions of this assignment is to consider a larger collection of energy pathways which reactants may take in the reaction. In this study, we only considered the minimum energy reaction pathway of each reaction, thus neglected the fact that molecules undergo many different collisions via many different pathways to actually react. A greater understanding of the reaction can therefore be gained by simulation of a greater number of possible reaction pathways.
References
- ↑ A. C. Cope and E. M. Hardy, J. Am. Chem. Soc., 1940, 62, 441-444. DOI:10.1021/ja01859a055
- ↑ S. Sakai, Int. J. Quant. Chem., 2000, 80, 1099-1106. DOI:10.1002/1097-461X(2000)80:4
- ↑ K. J. Shea and R. B. Phillips, J. Am. Chem. Soc., 1980, 102, 3156-3162 DOI:10.1021/ja00529a045
- ↑ R. Hoffmann and R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 2046-2048 DOI:10.1021/ja01087a034
- ↑ 5.0 5.1 5.2 J. M. Baranowski, J. Phys. C: Solid State Phys., 1986, 19, 4613-4621 DOI:10.1088/0022-3719/19/24/006
- ↑ D. Rowley and H. Steiner, Discuss. Faraday Soc., 1951, 10, 198-213. DOI:10.1039/DF9511000198.
