Year 3 Computational Lab: Physical Experiment

The protocol followed in this exercise can be found here.

The Cope Rearrangement Tutorial

1,5-hexadiene Optimisations

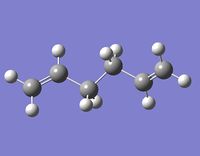
Figure 1: AntiA conformer equivalent to anti1

Anti Conformers

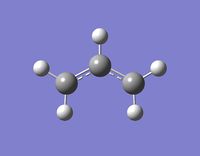
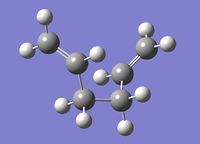
An anti 1,5-hexadiene molecule was optimised to a minimum at the HF/3-21G level of theory. This particular anti conformer (antiA) was found to be equivalent to anti1 in the table here. Anti1 in this table has an energy of -231.69260 a.u., which is very close to antiA's energy: -231.69260235 a.u.. They both have a point group C₂, and look the same. Figure 1 (right) is a picture of antiA, and its log file can be found here

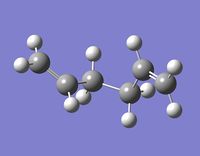
Figure 2: GaucheA conformer equivalent to gauche2

Gauche Conformers

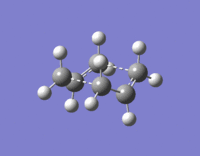
A gauche 1,5-hexadiene molecule was optimised to a minimum at the HF/3-21G level of theory. This particular gauche conformer (gaucheA) was found to be equivalent to gauche2 in the table here. Gauche2 in this table has an energy of -231.69167 a.u., which is almost the same as gaucheA, with a value of -231.69166 a.u.. This gaucheA structure and gauche2 have the same point group, C₂. Figure 2 shows of gaucheA, and its log file can be found ‎here

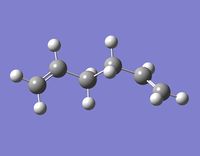
Finding the Lowest Energy Conformer

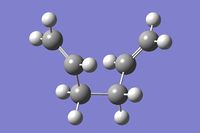
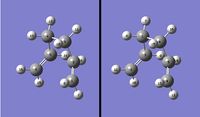
An attempt to find the lowest energy conformer was made by taking antiA (figure 1), chosen due to it being lower in energy than guacheA, and making the bond angles larger to reduce any steric effects. The structure was again optimised to a minimum at the HF/3-21G level. A picture of this molecule is shown in figure 3. The tweaks to the structure made little difference, but was very slightly lower, the new molecule having an energy of -231.69260237 a.u..

Further attempts to tweak the structure yielded a structure which was closer in energy to anti2, and so higher in energy than my original anti1 structure; energy of optimised structure (HF/3-21G optimisation to a minimum): -231.69253528 a.u., point group: C₁. This point group is not the same as that of anti2, which is investigated in the section below. The only anti conformer listed in the table with a C₁ symmetry is anti4, which looks nothing like my molecule, and has the significantly higher energy of -231.69097 a.u..

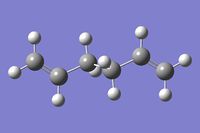
Figure 4: Fully optimised anti 2 structure

The anti2 Conformer

The attempt at drawing and optimising the anti2 structure as seen here was successful, giving a molecule of energy -231.69253527 a.u., which correlates well with the value given in the table of -231.69254 a.u.. Symmetrising the molecule gave a C_i point group, the same as that of the molecule in the table.

The anti2 molecule was then further optimised to a minimum at the B3YLP/6-31G* level, giving a significantly lower energy of -234.61170290 a.u., the point group remaining C_i. A picture of this reoptimised molecule is shown in figure 4, and its log file is available here. Table 1 (below) shows all relevant energies associated with this molecule (from both levels of optimisation).

All units in hartree	HF/3-21G					B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies (298.15 K)	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies (298.15 K)
anti2 from table	-231.692535	-231.539539			-231.532566	-234.611710	-234.469203			-234.461856
Calculated anti2	-231.69253527	-231.436741	-231.430933	-231.466250	-231.466250	-234.61170290	-234.469204	-234.461857	-234.460913	-234.500778

Table 1: Energies associated with the anti2 conformer; comparing previously reported data with new

Optimizing the Chair and Boat Transition States

Figure 6: Imaginary frequency of the chair transition state

Figure 9: Optimised point 44, same for both IRCs

Chair

An allyl fragment C₃H₅ was optimised to the HF/3-21G level of theory, giving a molecule of energy -115.82304010 a.u., which can be seen in figure 5 and who's log file can be found here. Using 2 units of this fragment, a chair transition state was guessed and optimised to a transition state using TSBerny to the HF/3-21G level of theory (chair optimisation A). This gave rise to a structure with an imaginary vibration of -817.9cm^-1 and energy of -231.61932230 a.u.. This imaginary vibration can be seen in figure 6, and it's log file can be found here. After this optimisation the bond making/breaking distances had dropped to 2.02Å.

The original (unoptimised) chair transition structure was then optimised to a minimum at the HF/3-21G level, freezing the 4 atoms involved in bond breaking/making (chair optimisation B). This gave a molecule of energy -231.61504992 a.u., which was then further optimised as a transition state with TSBerny to the HF/3-21G level (chair optimisation C), giving a molecule of energy -231.61932245 a.u. and imaginary frequency -817.96 cm^-1, the log file for this final optimised structure can be found here.

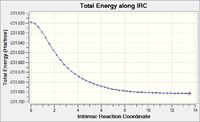
To find what structure a chair transition state is likely to drop to, an IRC was run forwards on this final optimised structure (from optimisation C), looking at 50 points, force constants being calculated all along the way at the HF/3-21G level of theory. The calculation stopped at point 44, giving the molecule shown in figure 7, of energy -231.69157878 a.u. and an RMS gradient of 0.00015223 a.u., log file available here. A graph of the total energies from this IRC can be seen in figure 8, clearly showing point 44 at a minimum. This molecule was then optimised to a minimum at the HF/3-21G level (chair optimisation D) to give a molecule of energy -231.69166702 a.u. and an RMS gradient of 0.00000475 a.u., log file: here.

An IRC was also run on our first optimised structure (from optimisation A) again looking at 50 points at the HF/3-21G level of theory. The calculation again stopped, this time at a structure of energy -231.69157869 a.u. at an RMS gradient of 0.00015227 a.u.. When this minimum was then optimised to a minimum at the HF/3-21G level (chair optimisation E), the same molecule as from optimisation D above was obtained, with energy: -231.69166702 a.u., point group C₂ and RMS gradient 0.00000475 a.u.. This final molecule can be seen in figure 9, and is equivalent to gauche2 in this table, being of the same energy, point group and conformation.

Boat

Figure 11: Set up of the two 1,5-hexadiene structures before the QST2 calculation - LHS: reactant, RHS: product

To obtain a structure for a boat transition state, the previously optimised anti2 structure was used as a skelton. The carbons were numbered appropriately and a TS(QST2) optimisation was run on the structures to find the Cope rearrangement (figure 10) transition state, which should be a boat. Initially this did not work as the anti2 structure had been left linear. The program could therefore not line up the appropriate orbitals and the calculation failed. The structures were therefore altered so that the atoms were correctly aligned for a Cope rearrangement (see figure 11). Using the atom labels in figure 11, the bond angles were changed to the following angles for the reactant molecule: C₂-C₃-C₄-C₅ to 0^o and C₂-C₃-C₄ & C₃-C₄-C₅ to 100^o. The product molecule's bond angles were similarly changed to: 0^o for C₂-C₁-C₆-C₅ and 100^o for C₂-C₁-C₆ & C₁-C₆-C₅. This worked well, and a boat transition structure was calculated. The boat had an energy of -231.60280168 a.u. and an imaginary frequency of -837.67cm^-1. This vibration can bee seen in figure 12.

Activation energies for boat and chair conformers

The chair structure from chair optimisation C was further optimised to a transition state to the B3YLP/6-31G* level of theory, to give a molecule of energy -234.55698303 a.u. with an imaginary frequency of -565.54 cm^-1. The boat structure obtained from the QST2 calculation was further optimised to a transition state to the B3YLP/6-31G* level, giving a molecule of energy -234.54309307 a.u., with an imaginary vibration of -530.37 cm^-1

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Units
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932245	-231.466701	-231.495207	-234.55698303	-234.414929	-234.443814	hartree
*Reactant (gauche2)*	-231.69166701	-231.538704	-231.570133	-234.61068811	-234.468263	-234.499305	hartree
ΔE gauche2 -> chair	0.07234456	0.072003	0.074926	0.05370508	0.053334	0.0579236	hartree
Boat TS	-231.60280168	-231.450928	-231.479774	-234.54309307	-234.402342	-234.431751	hartree
*Reactant (anti2)*	-231.69253527	-231.436741	-231.466250	-234.61170290	-234.469204	-234.500778	hartree
ΔE anti2 -> boat	0.08973359	0.014187	0.013524	0.06860983	0.066862	0.069027	hartree

The Diels Alder Cycloaddition

Optimisation of cis-Butadiene

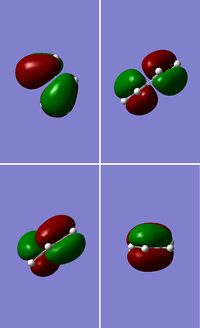
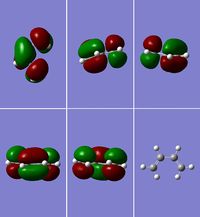
A molecule of cis-butadiene was drawn out, cleaned and optimised using the AM1 semi-empirical method, giving a molecule of energy 0.04878534 a.u. The HOMO and LUMO were visulalised, and can be seen in figures 13 and 14 respectively. The pictures in the first row of both figures cleary show the nodal planes of the two MOs, the HOMO having 2 and the LUMO having 3. The HOMO is clearly antisymmetric, whereas the LUMO is symmetric.

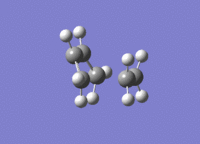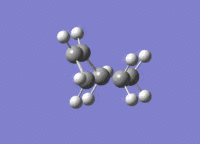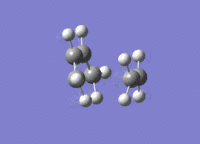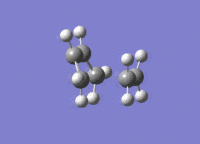
Figure 15: HOMO of Diels-Alder transition state

Figure 16: LUMO of Diels-Alder transition state

Transition State of "Prototype" Reaction

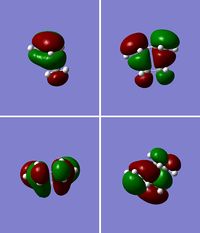
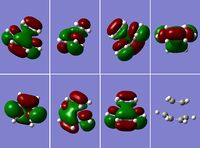
Using the previously optimised structure of cis-butadiene, the transition state for a Diels-Alder cycloaddition between cis-butadiene and ethylene was drawn out and optimised as a transition state with TSBerny at the semi-empirical AM1 level. The top right and bottom left pictures in figure 15 clearly show the 3 nodal planes of the HOMO of this transition state, whilst the nodal planes of the LUMO are much less clearly defined (figure 16); there are 2 nodal planes and 1 nodal curved surface which can be clearly seen in the picture of the second row, second from the left. Again, the HOMO is antisymmetric and the LUMO is symmetric. The energy for this transiton state is 0.11165465 a.u., it has an imaginary frequency of: -956.17 cm^-1 and a point group of C₁. The imaginary frequency can be seen in figure 17.

Studying the Regioselectivity of the Diels Alder Reaction

In this section we will investigate the Diels Alder reaction of cyclohexa-1,3-diene with maleic anhydride. The primary structure formed will be the endo adduct has the endo transition state is lower energy, but we will also invesigate the exo transition state.

Optimising the reactants

Semi-empirical AM1 optimisation

Cyclohexa-1,3-diene was drawn out and optimised at the semi-empirical AM1 level of theory, giving a molecule of energy 0.02771129 a.u.. Maleic anhydride was drawn out and optimised to the semi-empirical AM1 level aswell, giving a molecule of energy -0.12182418 a.u..

HF/3-21G & B3YLP/6-31G* optimisations

Cyclohexa-1,3-diene was drawn out and optimised to a minimum to the HF/3-21G level of theory, giving a molecule of energy -230.54323108 a.u.. This was then further optimised to a minimum to the B3YLP/6-31G* level, giving a molecule of energy -233.41893632 a.u.. Maleic anhydride was also optimised to a minimum twice; to HF/3-21G and then further to B3YLP/6-31G*, giving molecules of energy -375.10351323 a.u. and -379.28954468 a.u. respectively.

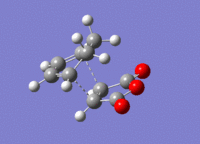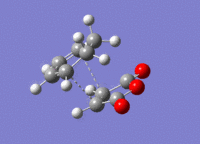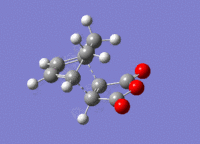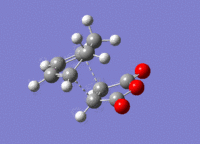
Figure 18: Imaginary frequency of exo maleicanhydride/cyclohexa-1,3-diene transiton state optimised by AM1

Figure 19: Bond lengths of the exo transition state optimised by AM1

Transition State Energies

3 Exo

Combining the structures from the semi-empirical AM1 optimisations

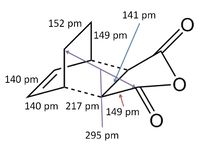
The structures previously optimised to AM1 were combined to give a transition state for an exo Diels Alder reaction. These were then optimised to a transition state with TSBerny to AM1, giving a transition state of energy -0.05041975 a.u. with an imaginary frequency of -812.67 cm^-1. This transition state can be seen in figure 18. The bond lengths of the C-C distances are shown in figure 19.

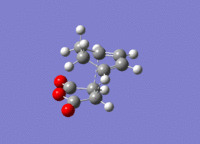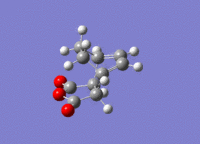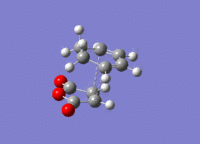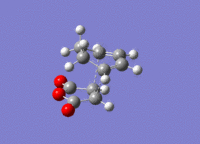
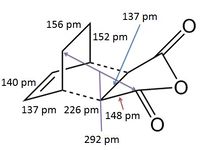
Figure 20: Imaginary frequency of the exo transition state optimised to HF/3-21G

Figure 21: Bond lengths of the exo transition state optimised by HF/3-21G

Combining the structures from the HF/3-21G & B3YLP/6-31G* optimisations

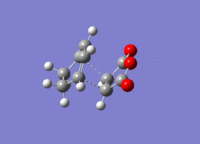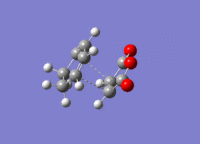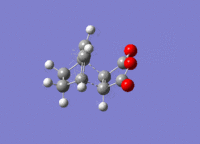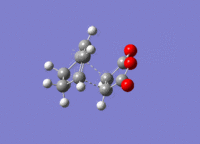
The structures previously optimised to the B3YLP/6-31G* level were combined to give a transition state for an exo Diels Alder reaction. These were then optimised to a transition state with TSBerny to HF/3-21G, giving a transition state of energy -605.60359124 a.u. with an imaginary frequency of -647.36 cm^-1. This transition state can be seen in figure 20.

A structure for the exo product was optimised to HF/3-21G level, giving a molecule of energy -605.71873542 a.u.. The two previously optimised (to B3YLP/6-31G*) reactants were placed in the same file in an exo orientation and a QST2 calculation was run to HF/3-21G to find the transition state, to compare with the guess structure shown in figure 20. The transition state from this calculation had an energy of -605.60359125 a.u. and an imaginary frequency of -647.48 cm^-1. Both of these values are close to the values determined by my guess structure, which would suggest that the guess was quite good. The bond lengths from this transition state can be seen in figure 21.

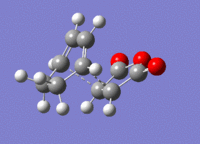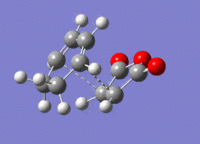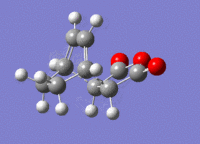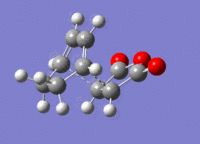
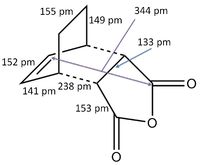
Figure 22: Imaginary frequency of the endo transition state optimised to AM1

Figure 23: Bond lengths of the endo transition state optimised by AM1

4 Endo

Combining the structures from the semi-empirical AM1 optimisations

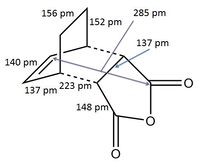
The structures previously optimised to AM1 were combined to give a transition state for an endo Diels Alder reaction. These were then optimised to a transition state with TSBerny to AM1, giving a transition state of energy -0.05150474 a.u.. with an imaginary frequency of -806.40 cm^-1. This transition state can be seen in figure 22. The bond lengths of the C-C distances are shown in figure 23.

Figure 24: Imaginary frequency of the endo transition state optimised to HF/3-21G

Figure 25: Bond lengths of the endo transition state optimised by HF/3-21G

Combining the structures from the HF/3-21G & B3YLP/6-31G* optimisations

The structures previously optimised to the B3YLP/6-31G* level were combined to give a transition state for an endo Diels Alder reaction. These were then optimised to a transition state with TSBerny to HF/3-21G, giving a transition state of energy -605.61036822 a.u. with an imaginary frequency of -643.58 cm^-1. This transition state can be seen in figure 24.

A structure for the endo product was optimised to HF/3-21G level, giving a molecule of energy 605.72132083 a.u.. The two previously optimised (to B3YLP/6-31G*) reactants were placed in the same file in an endo orientation and a QST2 calculation was run to HF/3-21G to find the transition state, to compare with the guess structure shown in figure 22. The transition state from this calculation had an energy of -605.61036811 a.u. and an imaginary frequency of -643.19 cm^-1. Both of these values are close to the values determined by my guess structure, which would suggest that the guess was quite good. The bond lengths from this transition state can be seen in figure 25.

References

The protocol followed in this exercise can be found here.