Rep:Mod:Y3CLKB10
Cope Rearrangement
The first part of this project examines different computation methods available for locating transition states and local minimum energy conformers. The following section summaries calculations conducted on Gaussian for 10 low energy conformers of 1,5-hexadiene, after which the chair and boat transition state structures were generated. Activation energies for the [3,3]-sigmatropic Cope rearrangement (below) via each transition state were calculated.
Optimising the Reactants and Products
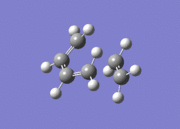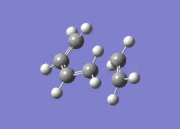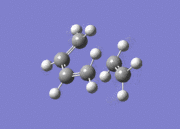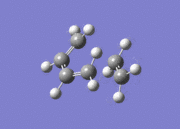
| File Name | lkb_apphexadiene_opt |  Identified as anti1conformer. Dihedral angle = 177.0°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.69260231 | |
| RMS Gradient Norm (a.u.) | 0.00002121 | |
| Dipole Moment (Debye) | 0.2023 | |
| Point Group | C2 | |
| Link to .log file | View File | |
| File Name | lkbanti3attempt |  Identified as anti3 conformer. Dihedral angle = 180°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.68907060 | |
| RMS Gradient Norm (a.u.) | 0.00001350 | |
| Dipole Moment (Debye) | 0.00 | |
| Point Group | C2h | |
| Link to .log file | View File | |
| File Name | lkbanti4attempt |  Identified as anti4 conformer. Dihedral angle = 178°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.69097056 | |
| RMS Gradient Norm (a.u.) | 0.00000979 | |
| Dipole Moment (Debye) | 0.2957 | |
| Point Group | C1 | |
| Link to .log file | View File | |
| File Name | lkbgauche1attempt |  Identified as gauche1 conformer. Dihedral angle = 75.7°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.68771616 | |
| RMS Gradient Norm (a.u.) | 0.00000601 | |
| Dipole Moment (Debye) | 0.4554 | |
| Point Group | C2 | |
| Link to .log file | View File | |
| File Name | lkbgauche2attempt |  Identified as gauche2 conformer. Dihedral angle = 64°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.69166700 | |
| RMS Gradient Norm (a.u.) | 0.00001388 | |
| Dipole Moment (Debye) | 0.3804 | |
| Point Group | C1 | |
| Link to .log file | View File | |
| File Name | lkb_gauchehexadiene_opt |  Identified as gauche3 conformer. Dihedral angle = 67.7° This is the lowest energy conformer of 1,5-hexadiene.
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.69266120 | |
| RMS Gradient Norm (a.u.) | 0.00001556 | |
| Dipole Moment (Debye) | 0.3409 | |
| Point Group | C1 | |
| Link to .log file | View File | |
| File Name | lkbgauche4attempt |  Identified as gauche4 Dihedral angle = 64°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.69153035 | |
| RMS Gradient Norm (a.u.) | 0.00000276 | |
| Dipole Moment (Debye) | 0.1281 | |
| Point Group | C2 | |
| Link to .log file | View File | |
| File Name | lkbgauche5attempt |  Identified as gauche5 conformer. Dihedral angle = 71°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.68961575 | |
| RMS Gradient Norm (a.u.) | 0.00000438 | |
| Dipole Moment (Debye) | 0.4437 | |
| Point Group | C1 | |
| Link to .log file | View File | |
| File Name | lkbgauche6attempt |  Identified as gauche6 conformer. Dihedral angle = 70°
|
| Calculation Type | FOPT | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.68916012 | |
| RMS Gradient Norm (a.u.) | 0.00002579 | |
| Dipole Moment (Debye) | 0.5363 | |
| Point Group | C1 | |
| Link to .log file | View File |
The anti2 conformer was constructed, by altering dihedral angles to give the approximate shape. Optimisation under the Hartree Fock 3-21G basis set generated a structure with the correct energy and point group. The molecule was then re-optimised under the B3LYP 6-31G(d) set and this affected the geometry as shown in the following table; the carbon-carbon bond lengths (Å) changed in the 2nd decimal place only, with the double bonds being lengthened and the single bonds being shortened.
| File Name | lkb_anti2attempt_opt |  |
lkb_anti2_opt_631gd |
| Calculation Type | FOPT | FOPT | |
| Calculation Method | RHF | RB3LYP | |
| Basis Set | 3-21G | 6-31G(d) | |
| Total Energy (a.u.) | -231.69253528 | -234.61171035 | |
| RMS Gradient Norm (a.u.) | 0.00001250 | 0.00001346 | |
| Dipole Moment (Debye) | 0.00 | 0.00 | |
| Point Group | Ci | Ci | |
| Calculation Time | 18s | 1min 36s | |
| Link to .log file | View File | View File |
| Bond | Distance (Å) | Anti2 conformer | |
|---|---|---|---|
| HF 3-21G | B3LYP 6-31G(d) | 
| |
| C1-C2 | 1.31616 | 1.33352 | |
| C2-C3 | 1.50891 | 1.50421 | |
| C3-C4 | 1.55286 | 1.54808 | |
| Angle | (°) | ||
| HF 3-21G | B3LYP 6-31G(d) | ||
| Dihedral (C2-C3-C4-C5) | 179.99 | 180.00 | |
| Inside (C1-C2-C3) | 124.81 | 125.29 | |
| Inside (C2-C3-C4) | 111.349 | 112.675 | |
| File Name | lkb_anti2_freq | 
|
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d) | |
| Total Energy (a.u.) | -234.61171035 | |
| RMS Gradient Norm (a.u.) | 0.00001346 | |
| Dipole Moment (Debye) | 0.00 | |
| Point Group | Ci | |
| Calculation Time | 2min 10sec | |
| Link to .log file | View File |
A frequency analysis was conducted on the 6-31G(d) optimised anti2 structure, to confirm that a minima had indeed been reached. All frequencies were positive and the low frequencies from the .log file have been presented below.
Low frequencies --- -9.4862 -0.0008 0.0006 0.0007 3.7428 13.0070 Low frequencies --- 74.2837 80.9994 121.4167
Also included here are the Thermodynamic details (enthalpies and energies) copied from the .log file.
The frequency calculation was repeated for T=0.01K by editing the input file, (setting temperature to exactly 0K caused the calculation to fail). This computed a "Sum of electronic and thermal energies" equivalent to the "Sum of electronic and zero-point energies" of the 298.15K calculation.
Default (298.15K, 1atm)
Zero-point correction= 0.142507 (Hartree/Particle) Thermal correction to Energy= 0.149853 Thermal correction to Enthalpy= 0.150797 Thermal correction to Gibbs Free Energy= 0.110933 Sum of electronic and zero-point Energies= -234.469204 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500777
Edited (0.01K, 1.0atm)
Zero-point correction= 0.142507 (Hartree/Particle) Thermal correction to Energy= 0.142507 Thermal correction to Enthalpy= 0.142507 Thermal correction to Gibbs Free Energy= 0.142507 Sum of electronic and zero-point Energies= -234.469204 Sum of electronic and thermal Energies= -234.469203 Sum of electronic and thermal Enthalpies= -234.469203 Sum of electronic and thermal Free Energies= -234.469203
The thermodynamic data for the original frequency calculation (default temperature) was accessed using the FreqChk utility on Gaussian. This allows for other temperatures to be investigated: setting T=0.01K computed the following corrections.
Zero-point correction= 0.127238 (Hartree/Particle) Thermal correction to Energy= 0.127238 Thermal correction to Enthalpy= 0.127238 Thermal correction to Gibbs Free Energy= 0.127239
Finding the Chair Transition State
An optimised allyl fragment was copied twice and positioned to resemble the chair transition state. This 'guess structure' was optimised via two different methods:
Whole Hessian
A guess structure for the transition state was constructed by places two optimised allyl structures next to each other, with a breaking/forming bond distance of approximately 2.2Å. An optimisation to a transition state (Berny) was carried out.
| Allyl Fragment | Guess Structure | Image of Guess Input | Image of Computed TS(Berny) | |
|---|---|---|---|---|
| File Name | LKB_ALLYL_OPTHF | LKB_CHAIR_TS_GUESS_OPT_FREQ |  |
|
| Calculation Type | FOPT | FREQ | ||
| Calculation Method | UHF | RHF | ||
| Basis Set | 3-21G | 3-21G | ||
| Total Energy (a.u.) | -115.82303994 | -231.61932233 | ||
| RMS Gradient Norm (a.u.) | 0.00008791 | 0.00002474 | 
| |
| Imaginary Frequency | n/a | 1 | ||
| Dipole Moment (Debye) | 0.0293 | 0.0005 | ||
| Point Group | CS | C1 | ||
| Calculation Time | 16s | 7s | ||
| Link to .log file | View File | View File |
Frozen Coordinate Method
The distance between the carbons which bond during reaction was frozen at around 2Å, using the redundant coordinate settings.
| Frozen Coordinates | Unfrozen Coordinates | Image of Computed Transition State | |
|---|---|---|---|
| File Name | LKB_CHAIR_GUESS_OPT_FREEZE | LKB_CHAIR_GUESS_OPT_UNFREEZE | 
|
| Calculation Type | FOPT | FREQ | |
| Calculation Method | RHF | RHF | |
| Basis Set | 3-21G | 3-21G | |
| Total Energy (a.u.) | -231.61470868 | -231.61932230 | |
| RMS Gradient Norm (a.u.) | 0.00340966 | 0.00340966 | |
| Dipole Moment (Debye) | 0.0002 | 0.0001 | |
| Imaginary Frequency | n/a | 1 | |
| Point Group | C1 | C1 | |
| Calculation Time | 25s | 7s | |
| Link to .log file | View File | View File |
The result of the Frozen Coordinate method was then reoptimised using the B3LYP 6-31G(d) method and basis set (summary below). This will be used in for inspecting activation energies and bond distances.
| File Name | LKB_CHAIR_TS_631GD.log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Total Energy (a.u.) | -234.55698298 |
| RMS Gradient Norm (a.u.) | 0.00002525 |
| Dipole Moment (Debye) | 0.00 |
| Imaginary Frequency | 1 (-566cm-1) |
| Point Group | C1 |
| Calculation Time | 1m 23s |
| Link to .log file | View File |
Effect on Bond Distance
The computed bond lengths for the different methods have been compared below, along a value from literature based on the Hartree Fock method. This shows that the methods examined do not all lead to exactly the same transition state. In order to determine which TS occurs at the maximum energy, and Intrinsic Reaction Coordinate calculation is required; this is explored in the next section.
| Breaking/forming C-C bond length (Å) | |
|---|---|
| Whole Hessian Method | 2.02 |
| Frozen Coordinate Method | 2.02 |
| 6-31G(d) Re-optimisation | 1.97 |
| Literature (3-21G Optimisation) | 2.062(Å)[1] |
Finding the Local Minimum
The Intrinsic Reaction Coordinate (IRC) method was used to locate the local minimum for the optimised 'guess' structure of the chair transition state (the Whole Hessian method). The set up was specified for the forward direction, with force constants calculated always, along 50 points.
| File Name | LKB_CHAIR_IRC.log | IRC/Path  |
LKB_GAUCHE2_321G.log | LKB_GAUCHE2_631GD |
| Calculation Type | IRC | FOPT | FOPT | |
| Calculation Method | RHF | RB3LYP | ||
| Basis Set | 3-21G | 6-31G(d) | ||
| Total Energy (a.u.) | -231.69157858 | -231.69166702 | -234.61068812 | |
| RMS Gradient Norm (a.u.) | 0.00015224 | 0.00000475 | 0.00003740 | |
| Dipole Moment (Debye) | 0.3630 | 0.3806 | 0.4389 | |
| Point Group | C1 | C2 | C2 | |
| Calculation Time (s) | 3min 43sec | 14sec | 42sec | |
| Link to .log file | View File | View File | View File |
The IRC curves shown above confirm that the computed transition state is indeed at a maximum, since the energy plot decreases from zero. The path lead to a geometry resembling the gauche2 conformer, but with a slightly higher energy; therefore the structure in the final step of the IRC (intermediate 44) was reoptimised using the Hartree Fock 3-21G method. The energy lowered and thus matched the given energy of the gauche2 conformer. This was structure again optimised using a higher basis set and method(B3LYP 6-31G(d)) which affected the bond distances as shown in the table below. (The IRC was also carried out on the 6-31G(d) frozen coordinate result, which produced a similar curve, but the product conformer had an even higher energy, sugguesting that it had fallen into the wrong minima).
| Method | C1=C2 Bond | C2-C3 bond | C3-C4 Bond |
|---|---|---|---|
| IRC | 1.32 | 1.51 | 1.55 |
| Hartree Fock | 1.32 | 1.51 | 1.55 |
| B3LYP | 1.33 | 1.54 | 1.55 |
Optimising the Boat Transition State
QST2 Method
The Ci (anti2) conformer was specified as reactant and product, and the atom numbers corrected, to correspond to the cope rearrangement.
An Opt+Freq calculation was set up, selecting the QST2 method, however this calculation did not generate the boat transition state. Instead it produced a more dissociated form of the chair (because the reactant is too far away from the geometry of the desired transition state). The structure is shown below, with a summary of the optimisation and link to the .log file.
| File Name | lkb_boat_qst2_fail | Input 
|
| Calculation Type | FREQ | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.61932240 | |
| RMS Gradient Norm (a.u.) | 0.00001535 | |
| Imaginary Frequency | 1 (-818cm-1) | Output 
|
| Dipole Moment (Debye) | 0.00 | |
| Point Group | C1 | |
| Calculation Time | 5s | |
| Link to .log file | View File |
By setting the central C-C-C-C dihedral angle of both molecules to 0° and the internal C-C-C angles to 100°, and running the calculation again successfully, a transition state was reached:
| File Name | LKB_BOAT_QST2_TWO.log | Input 
|
| Calculation Type | FREQ | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.60280222 | |
| RMS Gradient Norm (a.u.) | 0.00004230 | |
| Imaginary Frequency | 1 | Output 
|
| Dipole Moment (Debye) | 0.1584 | |
| Point Group | C1 | |
| Calculation Time | 7s | |
| Link to .log file | View File |
QST3 Method
A similar procedure was carried out as for the QST2 method, including a guess structure for the boat transition state which was constructed using two allyl groups placed parallel to each other, at a distance of ~2.2Å.
| File Name | LKB_BOAT_QST3.log | Input 
|
| Calculation Type | FREQ | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -231.60280245 | |
| RMS Gradient Norm (a.u.) | 0.00001700 | |
| Imaginary Frequency | 1 | |
| Dipole Moment (Debye) | 0.1583 | |
| Point Group | C1 | |
| Calculation Time | 7s | |
| Link to .log file | View File |
The resulting transition state structure was reoptimised, using the B3LYP method and 6-31G(d) basis set. Being more accurate, it is expected that reoptimising with this basis set would generate bond distances closer to those found in literature:
| File Name | lkb_boat_631G |
| Calculation Type | FTS |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Total Energy (a.u.) | -234.54309307 |
| RMS Gradient Norm (a.u.) | 0.00000445 |
| Imaginary Frequency | 1 |
| Dipole Moment (Debye) | 0.0613 |
| Point Group | C1 |
| Calculation Time | 2m 19s |
| Link to .log file | View File |
| Method | Breaking/forming bond distance |
|---|---|
| Hartree Fock | 2.14 |
| B3LYP | 2.21 |
Activation Energies
| HF 3-21G | B3LYP 6-31G(d) | ||||
|---|---|---|---|---|---|
| Chair TS | -231.61932230 | Chair TS | -234.55698298 | ||
| Gauche2 conformer | -231.69166702 | Gauche2 Conformer | -234.61068812 | ||
| Ea | 0.07234472 | 45.4kcal/mol | Ea | 0.05370514 | 33.7kcal/mol |
| Boat TS | -231.60280245 | Boat TS | -234.54309307 | ||
| Anti2 conformer | -231.69253528 | Anti2 Conformer | -234.61171035 | ||
| Ea | 0.08973283 | 56.3kcal/mol | Ea | 0.06861728 | 43.1kcal/mol |
| HF 3-21G | B3LYP 6-31G(d) | ||||
|---|---|---|---|---|---|
| Chair TS | -231.466702 | Chair TS | -234.414924 | ||
| Gauche2 conformer | -231.538705 | Gauche2 Conformer | -234.465710 | ||
| Ea | 0.072003 | 45.2kcal/mol | Ea | 0.050786 | 31.9kcal/mol |
| Boat TS | -231.450930 | Boat TS | -234.402342 | ||
| Anti2 conformer | -231.538321 | Anti2 Conformer | -234.469204 | ||
| Ea | 0.087391 | 54.8kcal/mol | Ea | 0.066862 | 42.0kcal/mol |
The table to the right shows the energies for both transition states and relevant conformers as computed under two basis sets. The activation energy has been calculated from the atomic unit energies and then converted into kcal/mol.
The same has been done for values at 0K (this information was retrieved from the .log files as the "sum of electronic and zero point energies"). The activation energies at 0K according to the higher basis set are consistent with experimental values (33.5kcal/mol for the chair and 44.7kcal/mol for the boat).
Diels Alder Cycloaddition
Butadiene and Ethylene
Optimisations
| Butadiene | Ethylene | Cyclohexene | |||
|---|---|---|---|---|---|
| File Name | BUT_AM1_OPT.log | BUT_HF_OPT.log | BUT_DFT631GD_OPT.log | ethyleneopt.chk | CYCLOHEXENE_631GD_OPT.log |
| Calculation Type | FOPT | ||||
| Calculation Method | RAM1 | RHF | RB3LYP | RB3LYP | RB3LYLP |
| Basis Set | ZDO | 3-21G | 6-31G(d) | 6-31G(d) | 6-31G(d) |
| Total Energy (a.u.) | 0.04879734 | -154.05394305 | -155.98594961 | -78.58745746 | -234.63289314 |
| RMS Gradient Norm (a.u.) | 0.00008900 | 0.00011857 | 0.00003238 | 0.00014423 | 0.000079145 |
| Dipole Moment (Debye) | 0.0414 | 0.0338 | 0.0852 | 0.00 | 0.3489 |
| Point Group | C1 | C1 | C2 | C1 | |
| Calculation Time | 10s | 7s | 15s | 1m 16s | |
| Link to .log file | View File | View File | View File | View File | |
Finding The Transition State
The following three methods for locating transition states were used. A guess structure was produced for these, by setting a bond breaking/forming bond distance of ~2Å. The Job Type used was Opt+Freq, force constants were calculated once, and all calculations resulted in one imaginary frequency at -818cm-1. For the whole hessian method, the "opt=noeigen" keyword was used.
| Whole Hessian Method | Frozen Coordinate Method | QST3 Method | Guess structure 
| |||
|---|---|---|---|---|---|---|
| File Name(DALDER_TS_GUESS_...) | ...HESSIAN | ...FREEZEHF | ...UNFREEZEHF | ...QST3HF | ...QST3 | |
| Calculation Type | FREQ | FOPT | FREQ | FREQ | FREQ | |
| Calculation Method | RHF | RHF | RHF | RHF | RB3LYP | |
| Basis Set | 3-21G | 3-32G | 3-21G | 3-21G | 6-31G(d) | |
| Total Energy (a.u.) | -231.60320830 | -231.62000042 | -231.60320854 | -231.60320843 | -234.54389650 | |
| RMS Gradient Norm (a.u.) | 0.00004777 | 0.01606331 | 0.00001797 | 0.00002621 | 0.00001570 | Computed Transition State 
|
| Imaginary Frequency | 1 | - | 1 | 1 | 1 | |
| Dipole Moment (Debye) | 0.5765 | 0.5605 | 0.5754 | 0.5761 | 0.3944 | |
| Point Group | C1 | C1 | C1 | C1 | C1 | |
| Calculation Time | 5s | - | 5s | 8s | ||
| Link to .log file | View File | View File | View File | View File | View File | |
| Method | Distance (Å) | Imaginary frequency vibration  |
Lowest positive frequency vibration 
|
|---|---|---|---|
| Whole Hessian(HF) | 2.209 | ||
| Frozen Coordinate(HF) | 2.210 | ||
| QST3 (HF) | 2.210 | ||
| QST3 (B3LYP) | 2.272 |
Typical bond lengths for sp2 and sp3 C-C bonds are 1.47Å and 1.54Å respectively[2]. The Van der Waals radius of a carbon atom is 1.70Å. [3].
The computed values are less than twice the Van der Waals distance, but greater than standard C-C sigma bond distances, confirming that there is a partially formed bond between the two carbons.
As can be seen from the imaginary frequency animation to the left, the formation of the two new sigma bonds in synchronous (concerted). This frequency is negative because it occurs at the transition state where the motion leads to a decrease in energy. In comparison, the lowest positive frequency shows an asynchronous formation, breaking symmetry and therefore leading to an increase in energy.
The resulting transition states from each of the above methods was analysed using anIRC calculation. The whole hessian produced a suitable set of curves, shown below, suggesting that the transition state is indeed at a maximum.
The QST3 method at highest basis set however did not produce the cyclic product when the IRC was carried out in both directions. This implies that the structure was not the correct transition state. A similar result was computed for the TS computed by the Frozen coordinate method.
| File Name | DALDER_TS_GUESS_HESSIAN_IRC.log | IRC/Path  |
|
| Calculation Type | IRC | ||
| Calculation Method | AM1 | ||
| Basis Set | ZDO | ||
| Total Energy (a.u.) | -231.72035001 | ||
| RMS Gradient Norm (a.u.) | 0.00014599 | ||
| Dipole Moment (Debye) | 0.2260 | ||
| Point Group | C1 | ||
| Calculation Time | 5m 27s | ||
| Link to .log file | View File |
Looking at the Molecular Orbitals
| HOMO | LUMO | Cartesian Axis | |||
|---|---|---|---|---|---|
| Butadiene | Ψ1: E = -0.22736 (a) |
Ψ2: E = -0.03013 (s) |
| ||
| Ethylene | Ψ3: E = -0.26667 (s)  |
Ψ4: E = 0.01881 (a) |
| ||
| Transition State | Ψ6 = Ψ 2+ Ψ3 E = -0.21897 (s)  |
Ψ7 = Ψ2 - Ψ3 E= -0.00860 (s)  |
Ψ5 = Ψ1 + Ψ4 E= -0.22107 (a)  |
Ψ8 = Ψ1 - Ψ4 E= 0.01963 (a)  |
|
| Cyclohexene | Ψ9: E = -0.22941 (s)  |
Ψ10: E = 0.04335 (a)  |
The molecular orbitals of reactants and transition states were computed in Gaussview and the results are presented in the table above. It can be seen that the 4 reactant orbitals can be combined in 4 different pairs: however, symmetry rules dictate that 2 of these are forbidden. Therefore the asymmetric butadiene HOMO and ethylene LUMO can be combined successfully, and the symmetric butadiene LUMO and ethylene HOMO may also be combined. Each pair produces 2 new orbitals (the MOs are both added AND subtracted) hence there are 4 relevant transition state MO's that should be examined.
Usually in textbooks there is only one interaction that is examined with regard to this reaction: the butadiene HOMO and the ethene LUMO, since this is the lowest energy difference out of the pairs with matching symmetry. The Salem-Klopman Equation[4] is used to determine other significant MO contributions, including non-bonding, and can be simplified to include only the HOMO-LUMO energy gap (all others being negligible).
However, as can be seen from the data, the asymmetric pair has an energy difference of 0.24617a.u. and the symmetric pair has a difference of 0.23654a.u. and these are too similar to justify simplifying the Salem-Klopman Equation. Instead both interactions are significant contributors to the reaction and this leads to the 4 transition states (two asymmetric and two symmetric).
Maleic anhydride and Cyclohexadiene
Optimisations
Molecules of Maleic anhydride, cyclohexa-1,3-diene and the two Diels-Alder adducts (exo and endo) were optimised, using the 6-31G(d) basis set. The adducts were first run on the lower level basis set (Semi Empirical, AM1).
| Maleic Anhydride | Cyclohexadiene | Endo Adduct | Exo Adduct | |||
|---|---|---|---|---|---|---|
 |
 |
 |
| |||
| File Name | MALEIC_631GD.log | CYCLOHEXADIENE_631GD | 4_ENDO_AM1.log | 4_ENDO_631GD.log | 3_EXO_AM1.log | 3_EXO_631GD.log |
| Calculation Type | FOPT | FOPT | FOPT | FOPT | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP | RAM1 | RB3LYP | RAM1 | RB3LYP |
| Basis Set | 6-31G(d) | 6-31G(d) | ZDO | 6-31G(d) | ZDO | 6-31G(d) |
| Total Energy (a.u.) | -379.28954470 | -233.41588484 | -0.16017089 | -612.75828992 | -0.15990932 | -612.75578522 |
| RMS Gradient Norm (a.u.) | 0.00000823 | 0.00007566 | 0.00001622 | 0.00004934 | 0.00002387 | 0.00004803 |
| Dipole Moment (Debye) | 4.0715 | 0.5484 | 5.5836 | 5.0187 | 5.2582 | 4.7591 |
| Point Group | C1 | C1 | C1 | C1 | C1 | C1 |
| Calculation Time | 1m 39s | 1m 9s | 1m 8s | 8m 41s | 19s | 9m 51s |
| Link to .log file | View File | View File | View File | View File | View File | View File |
The Endo Transition State
The QST3 Opt+Freq Method was used to locate the transition state for the Endo adduct. Force constance were calculated once. The calculation was initially carried out using the Hartree Fock method, and then the output was re-optimised using the B3LYP method. The following image shows the input structures for reactants (1), product (2), and a guess for TS(3). A summary of the calculation is given in this table.
| File Name | ENDO_QST3.log | Input 
|
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d) | |
| Total Energy (a.u.) | -612.68339618 | |
| RMS Gradient Norm (a.u.) | 0.00001585 | |
| Imaginary Frequency | 1 (-447cm-1) | |
| Dipole Moment (Debye) | 6.1145 | |
| Point Group | C1 | |
| Calculation Time | 26m 6s | |
| Link to .log file | View File |
Imaginary Frequency vibration |
Transition State |
Distances (Å) | |
|---|---|---|---|
| Breaking/Forming Bond (C2-C17) | 2.269 | ||
| Through space distance (C1-C22) | 2.990 | ||
| C1-C4 | 1.403 | ||
| C1-C2 | 1.391 | ||
| C2-C12 | 1.515 | ||
| C9-C12 | 1.558 | ||
| C16-C20 | 1.479 | ||
| C16-C17 | 1.394 | ||
The Exo Transition State
| File Name | EXO_QST3.log | Input 
|
| Calculation Type | FREQ | |
| Calculation Method | RHF | |
| Basis Set | 3-21G | |
| Total Energy (a.u.) | -605.60359119 | |
| RMS Gradient Norm (a.u.) | 0.00001383 | |
| Imaginary Frequency | 1 (-647cm-1) | |
| Dipole Moment (Debye) | 5.9364 | |
| Point Group | C1 | |
| Calculation Time | 2m 1s | |
| Link to .log file |
| File Name | EXO_QST3REOPT.log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Total Energy (a.u.) | -612.67931089 |
| RMS Gradient Norm (a.u.) | 0.00000809 |
| Imaginary Frequency | 1 (-448cm-1) |
| Dipole Moment (Debye) | 5.5494 |
| Point Group | C1 |
| Calculation Time | 8m 34s |
| Link to .log file |
Imaginary Frequency Vibration  |
Transition State  |
Bond Distances (Å) | |
|---|---|---|---|
| Breaking/forming bond (C3-C16) | 2.29071/2.29053 | ||
| Through space (C9-C20) | 3.02735/3.02733 | ||
| C1-C4 | 1.403 | ||
| C1-C2 | 1.391 | ||
| C2-C12 | 1.515 | ||
| C9-C12 | 1.558 | ||
| C16-C20 | 1.479 | ||
| C16-C17 | 1.398 | ||
Molecular Orbital Analysis
| HOMO | LUMO | |||
|---|---|---|---|---|
| Maleic Anhydride | E = -0.29928 (a) |
E = -0.11712 (a) |
HOMO (s) (AM1 ZDO METHOD) 
| |
| Cyclohexadiene | E = -0.20102 (a)  |
E = -0.01512 (s)
| ||
| Endo TS | E = - 0.24228 (a)  |
E = -0.06773 (a)  |
E = -0.26655 (s)  |
E= - 0.05262 (s) 
|
| Exo TS | E = -0.24246 (a)  |
E = -0.07841 (a)  |
E = -0.26312 (s)  |
E = -0.05187 (s) 
|
| Endo Product | E = -0.26689  |
E = 0.02560 
| ||
| Exo Product | E = -0.26433  |
E = -0.03117
|
The above images were computed in GaussView from the 6-31G(d) optimised reactants and the QST3 generated Transition States. The symmetries however are not all as expected; the HOMO and LUMO for maleic anhydride are both found to be antisymmetric with respect to the plane orthogonal to the carbon framework. It would be forbidden for either of these to interact with the symmetric cyclohexadiene LUMO.
Upon reoptimisation of the maleic anhydride structure under the AM1 basis set, a symmetric HOMO was computed (shown in the table above). It is expected that this is the MO which interacts with the diene LUMO. In the MO analysis (6-31G(d)) this shape appears two levels below the HOMO and has an energy of -0.33138 (it is the highest occupied symmetric orbital).
It should be noted therefore, that despite the B3LYP being considered more accurate, it can lead to a reordering of molecular orbitals and in fact a lower level basis set would compute MOs which fit better theoretically.
Secondary Orbital Overlap Effect
An examination of the endo and exo forms shown above would suggest that the exo form is more strained. The oxygen atoms are positioned closer to the sp3 carbons, and have more steric repulsion with the 4 hydrogen atoms compared to the endo form, where the oxygen atoms are positioned underneath sp2 carbons (with only one hydrogen that can move away more freely).
The theory of secondary orbital overlap effects is often used to explain the selectivity of the endo form, over the exo. However there is no experimental evidence for such effects and there have been alternative explanations as to why the endo form has a lower energy, such as solvent effects, steric interactions, hydrogen bonds, electrostatic forces.[5]
Conclusion
This investigation has provided an understanding of how to compute transition states for a set of reactants using different calculation methods. A comparison of these has shown that although higher basis sets generally provide more accurate optimisations, the location of a maxima is very much dependent on the input 'guess' structure.
It has also been possible to observe the orbital contributions to Diels Alder cycloaddition; in the case of butadiene reacting with ethene, the close energies between HOMO-LUMO pairs suggest that 2 interactions are major contributors. For the reaction of maleic anhydride and cyclohexadiene however the symmetric MO's provide a more significant contribution since the HOMO and LUMO of the products are symmetric.
In these calculations, solvent effects have been ignored. It would be expected that the activation energies would vary depending on the solvent (for example the cycloaddition would be faster in water due to a decreased activation energy).
References
- ↑ K. Morokuma, W.T. Borden, D. A. Hrovat; Chair and boat transition states for the Cope rearrangement. A CASSCF study; J. Am. Chem. Soc. 1988 110 (13), 4474-4475 DOI:10.1021/ja00221a092
- ↑ Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer. ISBN 978-3-86025-249-9.
- ↑ Rowland RS, Taylor R (1996). "Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from van der Waals radii". J. Phys. Chem. 100 (18): 7384–7391. DOI:10.1021/jp953141
- ↑ Fleming, I. (2010) Molecular Orbital Theory, in Molecular Orbitals and Organic Chemical Reactions, Reference Edition, John Wiley & Sons, Ltd, Chichester, UK. DOI:10.1002/9780470689493.ch1
- ↑ [J. I. García, J. A. Mayoral, L. Salvatella; 2000; Do Secondary Orbital Interactions Really Exist?; Acc. Chem. Res., 2000, 33 (10), pp 658–664 DOI:10.1021/ar0000152 ]