Rep:Mod:XYZ9241
NH3
Optimisation details
Optimised the N-H bond lengths and torsional angle in an ammonia molecule using B3YLP method that makes approximations to solve Schrodinger's equation.Basis set 6-31G(d,p) allows to have quick calculation with medium level accuracy
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986268D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
| Method | Result |
|---|---|
| Calculation | B3YLP |
| Basis set | 6-31G(d,p) |
| Type | OPTF |
| RMS Gradient | 0.00000485 a.u. |
| Energy | -56.55776873 |
| Bond lentgh | 1.01798 Å |
| Bond Angle | 105.74115° |
| Point Group | C 3V |
Jmol visualisation
Optimised NH3 |
Link to optimised log file here
Frequency Analysis
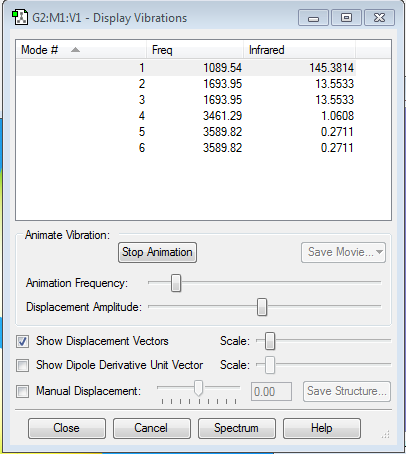
1)How many modes do you expect from the 3N-6 rule?
From the 3N-6 rule you expect 6 vibrational modes and effectively after Gaussian carries out the calculation there are 6 vibrational modes found.
2)Which modes are degenerate (ie have the same energy)?
The frequency of vibration is proportional to the energy of vibration, therefore modes 2 and 3 are degenerate and modes 5 and 6 are degenerate too as they have the same frequency.
3)Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Bending vibration modes are 1,2 and 3. Bond stretch vibration modes are 4,5 and 6.
4)Which mode is highly symmetric?One mode is known as the "umbrella" mode, which one is this?What would you see in an experimental spectrum?
The umbrella vibration is mode 1. Vibrational mode showing very high symmetry is mode 4 corresponding to symmetric stretches along the N-H bonds, but the umbrella mode is also highly symmetric.
You would expect to see 2 bands in a spectrum even though there are 4 different frequencies shown by Gaussian. This is because for modes 4,5 and 6 the intensities are negligible due to this type of vibrations generating a negligible change in dipole moment. Essentially they are IR inactive, whereas for modes 1,2&3 the change in dipole moment is much greater. However, 2&3 are degenerate so would see two peaks at around 1090cm-1 and 1694cm-1.
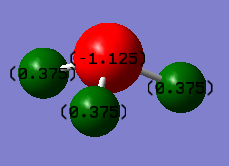
Charge Analysis
Negative charge on the nitrogen atom as it is more electronegative than hydrogen.Thus, withdraws electron density from the hydrogens to have an overall negative charge; N-H bond is polar covalent.
N2
Optimisation details
Item Value Threshold Converged?
Maximum Force 0.000145 0.000450 YES
RMS Force 0.000145 0.000300 YES
Maximum Displacement 0.000045 0.001800 YES
RMS Displacement 0.000064 0.001200 YES
Predicted change in Energy=-6.585142D-09
Optimization completed.
-- Stationary point found.
Optimised N2 molecule focusing on the bond length, using B3YLP method that makes approximations to solve Schrodinger's equation by using a basis set 6-31G(d,p) which allows to have a quick calculation method with medium level accuracy.
| Method | Result |
|---|---|
| Calculation | B3YLP |
| Basis set | 6-31G(d,p) |
| Type | OPTF |
| RMS Gradient | 0.00008380 a.u. |
| Energy | -109.52412897 a.u. |
| Bond lentgh | 1.1055Å |
| Bond Angle | 180° |
| Point Group | D ∞h |
Jmol Visualisation
Optimised N2 |
Link to optimised log file here
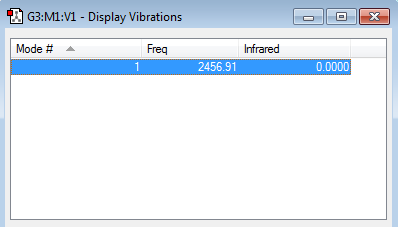
Frequency Analysis
There is one vibrational mode with frequency 2456.91 cm−1 corresponding to a symmetric stretch. Which agrees with the 3N-5 rule for linear molecules. Nonetheless, Nitrogen is a homonuclear diatomic molecule and has no dipole so there's no change in dipole moment caused by symmetric stretch so Nitrogen is IR inactive.
Charge Analysis
As expected in any homonuclear diatomic molecule there is no net dipole because both atoms have the same electronegativity, this means there's an even distribution of electron density around the molecule.
H2
Optimisation details
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-6.835424D-15
Optimization completed.
-- Stationary point found.
Optimised H2 molecule focusing on the bond length, using B3YLP method that makes approximations to solve Schrodinger's equation by using a basis set 6-31G(d,p) which allows to have a quick calculation method with a medium level accuracy.
| Method | Result |
|---|---|
| Calculation | B3YLP |
| Basis set | 6-31G(d,p) |
| Type | OPTF |
| RMS Gradient | 0.00000004 a.u. |
| Energy | -1.17853936 a.u. |
| Bond lentgh | 0.74279Å |
| Bond Angle | 180° |
| Point Group | D ∞h |
Jmol visualisation
Optimised H2 |
Link to optimised log file here
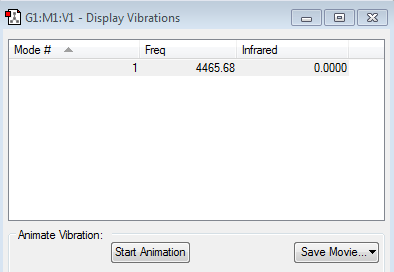
Frequency Analysis
There is one vibrational mode with frequency 4465.68cm−1 corresponding to a symmetric stretch. Which agrees with the 3N-5 rule for linear molecules. Nonetheless, Hydrogen is a homonuclear diatomic molecule and has no dipole so there's no change in dipole moment caused by symmetric stretch so Hydrogen is IR inactive.
Charge Analysis
As expected in any homonuclear diatomic molecule there is no net dipole because both atoms have the same electronegativity, this means there's an even distribution of electron density around the molecule.
Haber-Bosch Process
N2 + 3H2 ---> 2NH3
Process used in industry to synthesise Ammonia. Often in the presence of an Iron catalyst at high temperature (around 400K) and high pressure. Which are optimised conditions to obtain a good yield of Ammonia at a fast enough rate for commercial distribution.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= 2*(-56.55776873)-((-109.52412897)+3*(-1.17853936))=-0.05579041
ΔE=-0.05579041*2625.5=-146.48 kJ/mol
The standard literature value for enthalpy of formation gives -45.910kJ/mol [1] per mole of product therefore for the Haber process would be -91.82kJ/mol. However, the calculation carried out by Gaussian gives -146.48 kJ/mol this is due to the software considering the molecule at absolute zero and other different calculation limitations.
F2
Optimisation details
Item Value Threshold Converged?
Maximum Force 0.000074 0.000450 YES
RMS Force 0.000074 0.000300 YES
Maximum Displacement 0.000090 0.001800 YES
RMS Displacement 0.000128 0.001200 YES
Predicted change in Energy=-6.633870D-09
Optimization completed.
-- Stationary point found.
Optimised F2 molecule focusing on the bond length, using B3YLP method that makes approximations to solve Schrodinger's equation by using a basis set 6-31G(d,p) which allows to have a quick calculation method with medium level accuracy.
| Method | Result |
|---|---|
| Calculation | B3YLP |
| Basis set | 6-31G(d,p) |
| Type | OPTF |
| RMS Gradient | 0.00004246 a.u. |
| Energy | -199.49825219 a.u. |
| Bond lentgh | 1.40288Å |
| Bond Angle | 180° |
| Point Group | D ∞h |
Jmol visualisation
Optimised F2 |
Link to optimised log file here
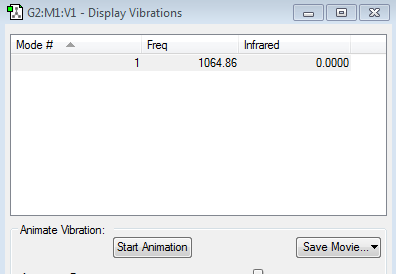
Frequency Analysis
There is one vibrational mode with frequency 1064.86 cm−1 corresponding to a symmetric stretch. Which agrees with the 3N-5 rule for linear molecules. Nonetheless, Fluorine is a homonuclear diatomic molecule and has no dipole so there's no change in dipole moment caused by symmetric stretch so Fluorine is IR inactive.
Charge Analysis
As expected in any homonuclear diatomic molecule there is no net dipole because both atoms have the same electronegativity, this means there's an even distribution of electron density around the molecule.
Molecular Orbitals
| Image | Description |
|---|---|
 |
Diagram showing relative energies of the MO's |
 |
Picture showing 2σu* antibonding orbital arising from the destructive interference between 2s orbitals in two Florine atoms. There's a node in the middle of the bond and the nature is ungerade as inversion symmetry comes along with a change in phase. |
 |
Picture showing the 3σg bonding orbital arising from the constructive interference between 2pz orbitals which point along the internuclear axis.There are two nodes, each crossing through each fluorine |
 |
Picture showing the 1πu bonding orbital arising from the constructive interference(sideways overlap) between 2px or 2py orbitals, to give two degenerate molecular orbitals of the same type. Ungerade nature, applying inversion symmetry gives change in phase. |
 |
Picture showing the 1πg* antibonding orbital arising from the destructive interference(sideways overlap) between 2px or 2py orbitals, to give two degenerate molecular orbitals of the same type. Gerade nature, applying inversion symmetry gives no change in phase.This is the HOMO level, using bond order rule (6-4)/2 = 1 so F-F is single bond. |
 |
Picture showing the 3σu* antibonding orbital arising from the destructive interference between 2pz orbitals along the internuclear axis.Ungerade nature, applying inversion symmetry gives change in phase.This is the LUMO level. |
Independent Molecule HCl
Optimisation details
Item Value Threshold Converged?
Maximum Force 0.000082 0.000450 YES
RMS Force 0.000082 0.000300 YES
Maximum Displacement 0.000127 0.001800 YES
RMS Displacement 0.000180 0.001200 YES
Predicted change in Energy=-1.050402D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.2863 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
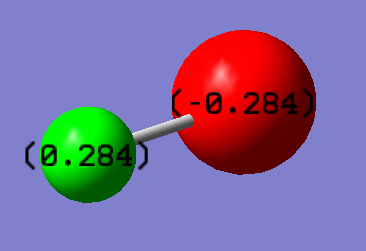
Optimised HCl molecule focusing on the bond length, using B3YLP method that makes approximations to solve Schrodinger's equation by using a basis set 6-31G(d,p) which allows to have a quick calculation method with medium level accuracy.
| Method | Result |
|---|---|
| Calculation | B3YLP |
| Basis set | 6-31G(d,p) |
| Type | OPTF |
| RMS Gradient | 0.00004760 a.u. |
| Energy | -460.80077875 a.u. |
| Bond lentgh | 1.28267 Å |
| Bond Angle | 180° |
| Point Group | C ∞h |
Jmol Visualisation
Optimised HCL |
Link to optimised log file here
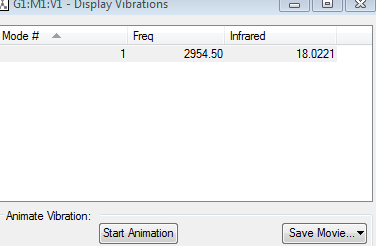
Frequency Analysis
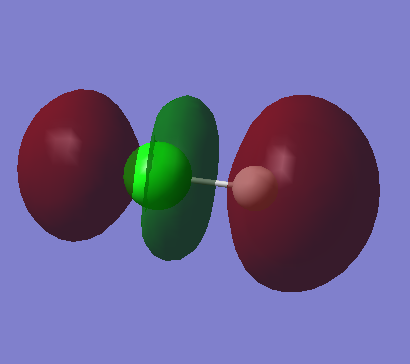
3N-5 rule gives one vibrational mode which corresponds to an assymmetric stretch along the H-Cl bond. H-Cl bond is already polar therefore the stretch gives a change in dipole moment and so the vibration is IR active at about 2954.50cm−1.
Charge Analysis
Cl is more electronegative than H so withdraws electron density, thereby the H-Cl bond is polar covalent.
Molecular Orbitals
| Image | Description |
|---|---|
 |
Bonding σ orbital arising from constructive interference between 3p orbital pointing along the internuclear axis in Chlorine and the 1s orbital in Hydrogen. There's greater electron density towards the chlorine atom as it is more electronegative so it resembles more the 3p orbital than the 1s. E= -0.84769 |
 |
This orbital seems to not quite fit in with what would be expected from a qualitative MO diagram. It is as if an extra orbital had been added as the energy of this orbital lies in between that of the σ and the non-bonding orbitals (E=-0.47429). Possible guess is that it might have to do something with ionic interactions due to the difference in electronegativity in this molecule. |
 |
Non bonding molecular orbital arising from the 3p orbitals in fluorine. There are two of these orbitals due to 3px and 3py which in this case aren't pointing along the internuclear axis. E=-0.33162 |
 |
σ* antibonding orbital due to destructive interference between the 3p orbital pointing along the internuclear axis from Fluorine and the 1s orbital from Hydrogen. E= 0.01356 |
 |
This correponds to the relative energies of the orbitals calculated by Gaussian |
- ↑ Sana, M.; Leroy, G.; Peeters, D.; Wilante, C. Journal of Molecular Structure, 1988 , vol. 164, p. 249 - 274