Rep:Mod:XYZ7777
Module 3: Characterisation of transition structures on potential energy surfaces
The aim of this computational experiment is to characterise the transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions. The computational experiments will be carried out using GaussView 5 following the online labscript at https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3.
The Cope Rearrangement Tutorial

Optimizing the Reactants and Products
The molecule of 1,5-hexadiene was drawn, with an anti and gauche linkage for the central four carbon atoms. The structure was optimised using the Hartree-Fock method and the 3-21G basis set.
1,5-hexadiene with an anti linkage

This molecular optimisation depicted an anti-perplanar (app) conformation of the middle 4 C atoms within the 6 carbon chain.
Point Group: C2
Energy: -231.68042 Ha
1,5-hexadiene with a gauche linkage

Point Group: C1
Energy: -231.68772 Ha
The symmetry of the gauche conformer was found to be C1, due to its lack of symmetry.
1,5-hexadiene contains three readily rotating carbon- carbon bonds. Each of these bonds has three rotational minima. The anti conformation is expected to be lower in energy, as this arrangement has the most conformers wherein the methylene groups are furthest away (What do your results say? João (talk) 18:23, 23 March 2015 (UTC)). However it has been found that the conformational energies of the anti and gauche 1,5-hexadiene are remarkably similar. This is because the Hartree-Fock method, with its lack of electron correlation, treats 1,5-hexadiene too much like n-butane to provide quantitative results. [1] (Are energy differences for n-butane conformers small? João (talk) 18:23, 23 March 2015 (UTC))
Prediction of lowest energy of 1,5-hexadiene based on previous results
The first optimisation procedure was carried by drawing with the middle 4 carbon atoms in a gauche conformation and by setting the dihedral angle to 60°. The optimisation of this structrue resulted in a high energy conformer with C1 symmetry.

The second optimisation resulted in the global minimum energy anti confomer, with both methylene groups pointing away from each other at 180°.
Both conformers were optimised using the dihedral angle tool in Gaussview.
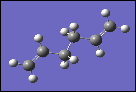
Point Group: Ci
Energy: -231.68029 Ha
Comparison of low energy conformers to those listed in Appendix 1
| Figure | Conformation | Appendix 1 | Energy (Ha) | Energy Appendix 1 | Point Group | RMS Gradient Norm (Ha) |
|---|---|---|---|---|---|---|
| 2 | anti a.p.p | Anti4 | -231.69260 | -231.69260 | C2 | 0.00001693 |
| 4 | optimised anti | Anti 2 | -231.69254 | -231.69254 | Ci | 0.00007782 |
| 3 | gauche | Gauche | -231.68772 | -231.68772 | C1 | 0.00004427 |
| 5 | optimised gauche | Gauche3 | -231.69266 | -231.69266 | C1 | 0.00006315 |
As can be seen in Table 1, the calculated energy and symmetry values correspond to those given in Appendix 1. All of the energies have identical values as stated in the Appendix, when rounded to five decimal places. The small deviations in energy after the fifth decimal place are however negligible and so it can be concluded that the optimised anti (anti2) has the lowest energy. (Is this what your results say? João (talk) 18:23, 23 March 2015 (UTC))
The tabulated results seem to contradict the conventional rules of organic chemistry, which indicate that the anti conformation should be the lowest in energy. As seen above, the energies of the anti conformations are particularly low in energy due to the restricted σ/σ* orbital overlap (Which σ and σ* could overlap? Aren't they orthogonal to each other? João (talk) 18:23, 23 March 2015 (UTC)). However in this case the Gauche3 conformer has the lowest energy of -231.69266 Ha. The reason for this discrepancy from conventional organic chemistry has been postulated by Gung et al. [2] The reason being the interaction between the π electrons of the carbon-carbon double bond and the nearby vinyl proton, termed the CH-π interaction. Overall there are 27 possible conformations, but only ten are energetically distinct. However the most interesting result is the near degeneracy of the energies of the four conformers. Furthermore it can be concluded that the optimisations were carried out successfully the RMS Gradient Norm is very small.
Reoptimization using DFT method at the B3LYP/6-31G* level
The Ci anti2 conformation of 1,5-hexadiene is reoptimized with the more advanced DFT (Density Functional Theory) method and the higher basis set B3LYP/6-31G*. The calculated energies at the HF/3-21G level and B3LYP/6-31G* level are shown in Table 2.
| Basis Set | Hartree | RMS Gradient Norm (Ha) |
|---|---|---|
| HF/3-21G | -231.69254 | 0.00005923 |
| B3LYP/6-31G* | -234.61172 | 0.00009137 |
The reported energy of the optimised conformer using B3LYP/6-31G* is -234.61172 Ha. This energy is lower than the -231.69254 Ha, which were calculated using the HF/3-21G method. There is almost a 3 Ha energy difference when using the more advanced basis set. Hence it can be concluded that the B3LYP/6-31G* level should always be used when comparing configurational energies, as in the previous calculation the HF/3-21G method gave near degenerate results for all four conformations. Again it can be concluded that the optimisation calculation was carried out successfully as the RMS Gradient Norm is very small.
The obtained energies for the same confomer are very different, however cannot be compared relative to each other as the HF and DFT are two different methods, which use different assumptions, approximations and calculations. (Didn't you do exactly that in the paragraph above? João (talk) 18:23, 23 March 2015 (UTC))
It can be concluded that the optimisation is complete when it has converged. At this point the minimum energy has been found. The distinct convergence criteria, which prevent a premature identification of the minimum, are: Firstly the forces must be 0. Secondly the root mean square of the forces, the calculated displacements and the root mean square of the displacements must be below the defined threshold value (Ha). (Wouldn't a maximum satisfy exactly the same criteria? João (talk) 18:23, 23 March 2015 (UTC))
Inspection of the .log file and checking these criteria, it can be concluded that ‘’anti2’’ is has the minimum energy.

Observed change in geometry using the DFT method and reoptimising anti2 at the B3LYP/6-31G* level
There is certainly an observable change in bond geometry when reoptimising ‘’anti2’’ using the DFT method at the B3LYP/6-31G* level. The bond lengths and bond angles are affected, with the C=C in the 3-21G basis set being shorter than the 6-31G* basis set by 1Å (I would have agreed that 1Å change in bond length would have been a very important difference, but your results show a change which is one hundred times smaller. João (talk) 18:23, 23 March 2015 (UTC)), as seen from the values in Table 3.
The limitation of HF theory is the HF approximation itself, namely the independence of electrons. Generally the accuracy of results depends on the degree of electron correlation and the size of the basis set used. Hence why the DFT method at using the 6-31G* basis set gives more accurate results than the HF method using the smaller 3-21G basis set.
In summary the HF method and 3-21G basis set can only determine a near energy-minimum. A limitation of this method is that it cannot accurately find the point on the potential energy surface at which the first derivative is zero (Didn't you show above calculations at a Hartree-Fock level with a negligible gradient? The issue is that a geometry with a zero gradient at one level of theory may not be the same at another level of theory. João (talk) 18:23, 23 March 2015 (UTC)), meaning while it can determine a near energy-miniumum, the HF method gives an optimised structure, which is very close to the energetic and geometric minimum. The higher 6-31G* basis set however optimises closer to the energetic and geometric minimum, which corresponds to a point on the potential energy surface which has a positive second derivative.

Overall the single C-C bonds are longer in the HF/3-21G calculation, while the double C=C bonds are longer in the B3LYP/6-31G* level of theory. Furthermore, the bond angles between each set of 3 carbon atoms, as listed below, are all calculated to be larger using the DFT method at the B3LYP/6-31G* level of theory.
The set of bond lengths and bond angles tabulated in Table 3 imply that the conformation has Ci symmetry.
| Carbon Atoms | HF Bond Length (Å) | DFT Bond Lnegth (Å) | Torsion Angle | HF torsional Angle | DFT torsional Angle |
|---|---|---|---|---|---|
| C1-C2 | 1.32 | 1.33 | C1-C3 | 124.8 | 125.3 |
| C2-C3 | 1.51 | 1.50 | C2-C4 | 111.4 | 112.7 |
| C3-C4 | 1.55 | 1.55 | C3-C5 | 111.4 | 112.7 |
| C4-C5 | 1.51 | 1.50 | C4-C6 | 124.8 | 125.3 |
| C5-C6 | 1.32 | 1.33 |
Optimisation and frequency analysis of Anti2 conformer using DFT B3LYP/6-31G* theory
The frequency calculation is used to characterize the critical point, i.e. to confirm that it is a minimum. It does this by confirming that all vibrational frequencies are real and positive.
The first is the sum of electronic and zero-point energies, which correspond to the potential energy at 0K and the zero-point energy (E = Eelec+ZPE). The second is the energy contribution from the translational, rotational and vibratiinal energy modoes at 298.15K and 1 atm (E = E + Etrans + Erot + Evib). The third of which, includes correction for room temperature (H = E + RT ) and the last includes contribution from entropy (G = H - TS).
As seen in Figure 8, there are no imaginary frequencies. While some frequencies have zero intensity this can be explained by a dipole moment or a change in symmetry, which would both be IR inactive and result in zero intensity.

An IR frequency was then carried out on the B3LYP/6-31G(d) resulting in the following simulated IR spectrum, depicting peaks at real frequencies, with no imaginary ones.

Using the output file under the section thermochemistry the following was obtained:
Sum of electronic and zero-point Energies= -234.469273
Sum of electronic and thermal Energies= -234.461482
Sum of electronic and thermal Enthalpies= -234.460581
Sum of electronic and thermal free Energies= -234.500241
Optimizing the "Chair" and "Boat" Transition Structures


In this section a transition structure optimization is performed using three different methods:
(i) by computing the force constants at the beginning of the calculation
(ii) using the redundant coordinate editor
(iii) using QST2.
Furthermore this section aims to visualize the reaction coordinate, run the IRC (Intrinisic Reaction Coordinate) and calculate the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures.
Draw an allyl fragment (CH2CHCH2) and optimize it using the HF/3-21G level of theory
Here two allyl fragments with C2v symmetry were create and optimized using the HF/3-21G level of theory. Next the fragments were combined and oriented so that they look roughly like the chair transition state. The distance between the terminal ends of the allyl fragments is approximately 2.2 Å apart. This is only an approximate value due to the vibration of the molecule, which causes the terminal ends of the allyl fragments to have an alternating intermolecular distance of 2.2Å and 2.4Å.

Optimization to a TS (Berny)
A HF/3-21G Gaussian optimization is set up for the chair guess structure in order to: Optimise to a TS (Berny). ‘Opt=NoEigen’ is inserted into Additional keyword box at the bottom, which stops the calculation crashing if more than one imaginary frequency is detected during the optimization which can often happen if the guess transition structure is not good enough.
The optimised TS can be seen below. It has a total energy of -231.61943 Ha and C2h symmetry. From the animation of the TS it can be seen that the optimisation has decreased the distance between the two terminal carbons on the allyl fragments. The distance between the terminal ends of the allyl fragments, which was approximately 2.2Å, is now approximately 2.02Å.
The frequency calculation should gives an imaginary frequency of magnitude -818.1 cm-1, which corresponds to an asymmetrical motion of the chain of six carbons forming and breaking and is characteristic of the Cope rearrangement.
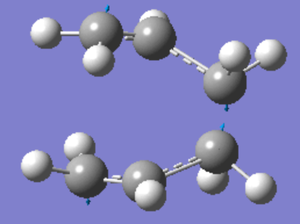

The frozen co-ordinate method
Again the ‘guess structure’ was copied into a new window to run this method. The 'Redundant Coord Editor' was used to ‘Create a New Coordinate’ and select two of the terminal carbons from the allyl fragments which form/break bonds during the Cope rearrangement. The command ‘Freeze Coordinate’ was assigned to the selected carbon bond. The distance between the two allyl fragments was set to 2.2Å.This procedure was repeated for the opposite terminal carbons.This method essentially freezes the forming bonds between the two allyl fragments to 2.2Å, and runs an minimum optimisation on the rest of the structure.
This resulted in a structure similar to that previously determined, with the bond lengths at exactly 2.2Å and an energy of -231.61523 Ha. Following this, the 'Redundant Coord Editor' was opened again, and this time the selected carbons were set to 'bond' and 'derivative'. From this, a TS HF/3-21G optimisation was carried out, again the ‘Opt=NoEigen’ is inserted into Additional keyword box . (Would you think that this keyword would be equally important in this case? João (talk) 18:23, 23 March 2015 (UTC))
Overall the two methods give almost identical results and structure. Both results contain imaginary frequencies, which implies the presence of a TS. In both cases, the terminal C atoms in the optimised structure were shown to be 2.02Å apart with a C-C-C bond angle of 120° and an energy of -231.61943 Ha and C2h symmetry.
In general, the two methods are very similar. The ways in which they differ is that the Hessian only works effectively when the ‘guess structure’ strongly resembles the actual TS, while the Frozen Coordinate method allows for the rest of the molecule to be optimised before searching for the TS. Hence the Frozen Coordinate method is better when the exact structure of the TS in unknown.
Optimization of the boat transition structure
In this section, the ‘’boat’’ TS will be optimised. In order for this procedure to be successful, the reactant and product atoms must be numbered in the following way:

As illustrated the bonds between the atoms change but the position of the atoms stays the same. This was done using the Atom List Editor. The two molecules of the optimised anti2 1,5-hexadiene could be viewed side by side and placed in such a way as to be mirror images of each other, as shown below.

After numbering the mirror image conformers, the following commands are set up:
Type: OPT+FREQ
Optimisation to a: TS (QST2)
Calculate Force Constants: Never (I'm somewhat surprised that the calculation converged without having calculated the force constants. João (talk) 18:23, 23 March 2015 (UTC))
Additional Keywords: Opt=NoEigen
Once submitted, the job fails. The opened chk file looks like a dissociated chair transition structure. The reason for the job failing is that the calculation linearly interpolated between the two structures and simply translated the top allyl without considering the possibility of a rotation around the central bonds. It is clear that the QST2 method cannot locate the boat transition structure when starting from these reactant and product structures.
Hence the reactant and product geometries need to be modified so that they are closer to the boat transition structure. The central C-C-C-C dihedral angle is changed to 0°. Then select the inside C-C-C angles are reduced to 100°. The job is resubmitted following QST2 method to yield the final boat TS structure.

One imaginary frequency was found at -839.2cm-1. The C-C distance for both terminal carbon pairs was found to be 2.14Å and the structure was shown to have an energy of -231.60281 Ha and C2V symmetry.
The Intrinsic Reaction Coordinate method
The Intrinsic Reaction Coordinate method (IRC) is a method implemented in Gaussian can follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This creates a series of points by taking small geometry steps in the direction where the gradient of the energy surface is steepest.
This calculation was attempted with 50 points, however it did not converge. Hence, the job was carried out again whilst calculating the force constant at every single point. As seen below, the RMS Gradient of the energy falls to zero implying that a minimum has been reached. (Which of the different possible minima was obtained? João (talk) 18:23, 23 March 2015 (UTC))
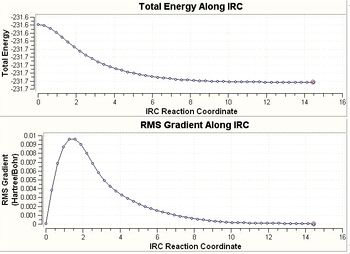
Calculating the TS activation energies
Finally the activation energies are calculated for the Cope Reaction via both transition structures. To do this the chair and boat transition structures need to be reoptimised using the B3LYP/6-31G* level of theory starting from the HF/3-21G optimized structures. Frequency calculations are then carried out. (Did these confirm the structures as transition states? By how much did the transition state geometry change? João (talk) 18:23, 23 March 2015 (UTC))
Chair TS B3-LYP/6-31G
Sum of electronic and zero-point energies = -234.414664
Sum of electronic and thermal Energies = -234.409275
Sum of electronic and thermal Enthalpies = -234.307016
Sum of electronic and thermal Free Energies = -234.443892
Chair TS B3-LYP/6-31G
Sum of electronic and zero-point energies = -234.402938
Sum of electronic and thermal Energies = -234.396132
Sum of electronic and thermal Enthalpies = -234.395035
Sum of electronic and thermal Free Energies = -234.431100
| Structure | HF/3-21G optimisation energy (Ha) | B3-LYP/6-31G optimisation energy (Ha) |
|---|---|---|
| anti2 | -231.6925 | -234.6117 |
| chair | -231.6194 | -234.5570 |
| boat | -231.6028 | -234.5431 |
The data also suggests that the B3LYP/6-31G* level of theory correlates much better with the experimental values. This is expected since the DFT method uses a larger basis set.
The tabulated activation energies show that the cope rearrangement will preferably proceed via the low energy chair TS. Since both TS lead to the same product, the chair TS is favoured, because it has the lower energy.
| HF/3-21G | B3-LYP/6-31G | Experimental | |
|---|---|---|---|
| ΔE Chair (kcal/mol) | 45.71 | 34.05 | 33.5 ± 0.5 |
| ΔE Boat (kcal/mol) | 55.60 | 41.94 | 44.7 ± 2.0 |
Diels Alder Cycloaddition
This section of the report involves the investigation into the Diels Alder cycloaddition of ethylene and cis-butadiene, followed by the regioselective Diels Alder of cyclohexa-1,3-diene and maleic anhydride.
The Diels Alder reaction is a pericyclic reaction, specifically a cycloaddition. A Diels Alder Reaction results in the formation of two σ bonds, which stems from the interaction between the HOMO/LUMO (π/π*) orbitals of a diene and dienophile. A Diels Alder involves the transfer of an electron from one orbital to that of another molecule, leading to the formation of a new σ or π bond, depending on the interacting molecules. In the cases where electron transfer occurs, the two MO’s involved must either symmetric or anti-symmetric with respect to the bisecting plane of symmetry. Equally secondary orbital interactions such as the electrostatic interaction between an occupied and unoccupied orbitals enhances the stability of orientation over another.

Cis Butadiene

Cis butadiene is drawn and optimized B3LYP/3-61G* level of theory using Gaussian. As depicted below, the HOMO and LUMO of cis butadiene were visualized in order determine their symmetry with respect to plane. As seen the HOMO is asymmetrical (More than asymmetrical, the orbital is anti-symmetric with respect to the place of symmetry João (talk) 18:23, 23 March 2015 (UTC)) and the LUMO is symmetrical.


Computation of the Transition State geometry
In order to optimize the transition state a guess structure was established. The carbon atoms, which are to form the new σ bonds were frozen at 2.2AÅ. The rest of the molecule was optimized to a TS (Berny) at the B3LYP-3-61G* level.
The distance3 between terminal carbon atoms in the resulting transition structure is approximately 2.12Å. This is much longer than a typical C-C bond, however this is expected since the product has not yet been formed. At this point no equilibrium bond length can be established. However it must also be added that 2.12Å is smaller than two VdW radii of carbon, which is roughly 1.7Å. So while on one hand no equilibrium bond length can be established, a distance of 2.12Å implies some form of bonding interaction.

The frequency analysis reveals an imaginary vibration, which proves that this is a transition state structure. The vibration below show the movement of the carbons which are to form the new sigma bonds bending towards each other. It can be therefore said that the two new bonds are formed simultaneously.

The movement of the lowest positive frequency differs in that it is simply an asymmetric twisting motion of both fragments.

With respect to the bisecting plane, the HOMO of the TS is asymmetric. It is created from the HOMO of Butadiene and the LUMO of ethylene. Hence the TS LUMO will be symmetric and will be created from the LUMO of Butadiene and the HOMO of ethylene. (Is this what you actually obtain? João (talk) 18:23, 23 March 2015 (UTC))

(Why does the reaction occur? João (talk) 18:23, 23 March 2015 (UTC))
Cyclohexa-1,3-diene and maleic anhydride

Cyclohexa-1,3-diene react with maleic anhydride to give an endo product. This reaction is kinetically controlled, meaning it proceeds via the lowest egergy TS. While the exo product thermodynamically more stable the endo TS has a lower energy and is thus the favoured transition structure. (Did you find the transition states of this reaction to confirm these findings? João (talk) 18:23, 23 March 2015 (UTC))

Further Discussion
By definition, the Diels Alder reaction does not proceed via an ionic intermediate. It is because of this that the interaction of reagents with solvents is low. Despite the interaction being low, in this computational lab however, interactions with solvents have not been considered at all. While Diels Alder reactions don’t need solvent to react, the addition of water or other reagents has been proven to increase the rate of reaction as well as increase endo selectivity. [3]
- ↑ Koide, A., W. J. Meath, and A. R. Allnatt. "Molecular physics: An international journal at the interface between chemistry and physics." Molecular Physics 39.4 (1980): 895-911.
- ↑ Gung, B., W., Zhu ,Z., and Fouchr, A., 1995, J. Am. chem. Soc., 117, 1783.
- ↑ J. Clayden, N. Greeves and S. Warren in Organic Chemistry, Oxford University Press, 2nd edn., 2012, pp. 886-888.
