Rep:Mod:XYZ4869
NH3 Molecule
The ammonia molecule is investigated in the Gaussview to identify some properties of it, including bond length and bond angle. The following is the summary of the properties after optimizing by the calculation method, RB3LYP. The vibration modes and charge are also investigated in the Gaussview and the discussion is shown below.
Molecule: NH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient: 0.00000485 a.u.
Point Group: C3V
Bond length of N-H: 1.01798 Å
Bond angle of H-N-H: 37.129 °
Item Value Threshold Converged?<br>
Maximum Force 0.000004 0.000450 YES<br>
RMS Force 0.000004 0.000300 YES<br>
Maximum Displacement 0.000072 0.001800 YES<br>
RMS Displacement 0.000035 0.001200 YES<br>
Predicted change in Energy=-5.986294D-10<br>
Optimization completed.<br>
-- Stationary point found.<br>
----------------------------<br>
! Optimized Parameters !<br>
! (Angstroms and Degrees) !<br>
-------------------------- --------------------------<br>
! Name Definition Value Derivative Info. !<br>
--------------------------------------------------------------------------------<br>
! R1 R(1,2) 1.018 -DE/DX = 0.0 !<br>
! R2 R(1,3) 1.018 -DE/DX = 0.0 !<br>
! R3 R(1,4) 1.018 -DE/DX = 0.0 !<br>
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !<br>
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !<br>
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !<br>
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !<br>
--------------------------------------------------------------------------------<br>
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
NH3 molecule |
The optimisation file is liked to here
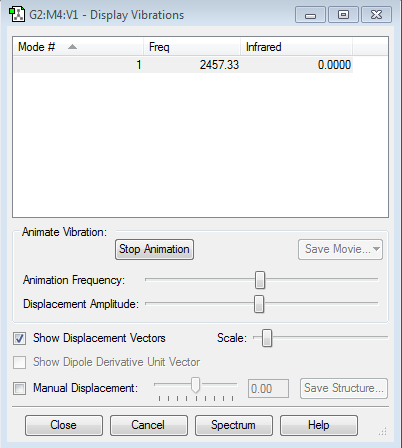
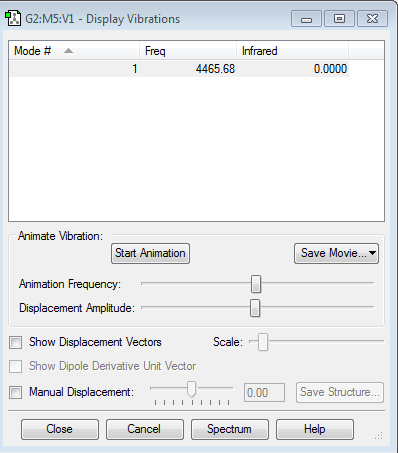
how many modes do you expect from the 3N-6 rule? 6 which modes are degenerate (ie have the same energy)? Asymmetric stretching(5,6), scissoring(2,3) which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending:1,2,3; Bond stretch: 4,5,6 which mode is highly symmetric? 4 one mode is known as the "umbrella" mode, which one is this? 1 how many bands would you expect to see in an experimental spectrum of gaseous ammonia? 2, the modes of 4,5 and 6 are too small to be identified, and the modes of 2 and 3 are the same.
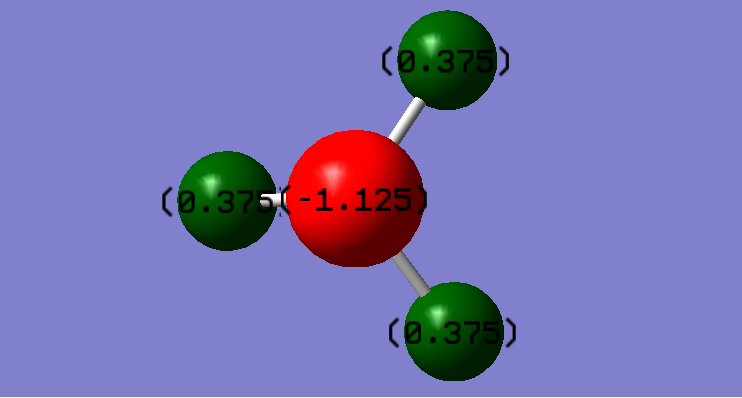
Nitrogen is negative due to higher electronegativity, while hydrogen is postive due to lower electronegativity.
N2 Molecule
The nitrogen molecule is optimized to find the final energy, which is used in calculating energy in the Haber-Bosch process. The optimization results and the vibration mode are shown below.
Molecule: N2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -109.52412868 a.u.
RMS Gradient: 0.00000060 a.u.
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.383696D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Only stretching occurs.
N2 molecule |
The optimisation file is liked to here
H2 Molecule
The hydrogen molecule is optimized to find the final energy, which is used in calculating energy in the Haber-Bosch process. The optimization results and the vibration mode are shown below.
Molecule: H2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Point Group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Only stretching occurs.
H2 molecule |
The optimisation file is liked to here
Haber-Bosch process
The process of calculating the energy of Haber-Bosch process is shown below.
E(NH3)= -56.55776873 a.u. 2*E(NH3)= -113.115537 a.u. E(N2)= -109.52412868 a.u. E(H2)= -1.17853936 a.u. 3*E(H2)= -3.53561808 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579024 a.u. =-146.48 KJ/mol
CH4 molecule
Another small molecule, methane, is also investigated in the Gaussview. It is optimized to find some properties of methane molecule. The vibration modes are also investigated and discussed below. The charges of carbon and hydrogen in the methane are shown in the picture below. The molecular orbitals of methane are discussed below.
Molecule : CH4
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -40.52401404 a.u.
RMS Gradient: 0.00003263 a.u.
Point Group: TD
Item Value Threshold Converged?
Maximum Force 0.000063 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.000179 0.001800 YES
RMS Displacement 0.000095 0.001200 YES
Predicted change in Energy=-2.256034D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.092 -DE/DX = -0.0001 !
! R2 R(1,3) 1.092 -DE/DX = -0.0001 !
! R3 R(1,4) 1.092 -DE/DX = -0.0001 !
! R4 R(1,5) 1.092 -DE/DX = -0.0001 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
CH4 molecule |
The optimisation file is liked to here
how many modes do you expect from the 3N-6 rule? 9 which modes are degenerate (ie have the same energy)? 1, 2 and 3; 4 and 5; 7, 8 and 9 which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending:1,2,3,4 and 5; Bond stretch: 6,7,8 and 9 how many bands would you expect to see in an experimental spectrum 2, first three modes and last three modes have same dipole moment so only two will be shown on the spectrum. The last column of modes 4, 5 and 6 are 0, which means that they are IR inactive, and the dipole moments cancelled out.
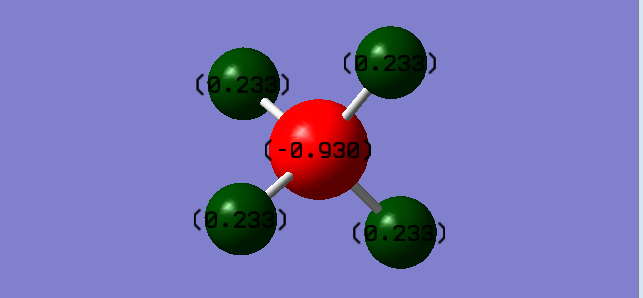
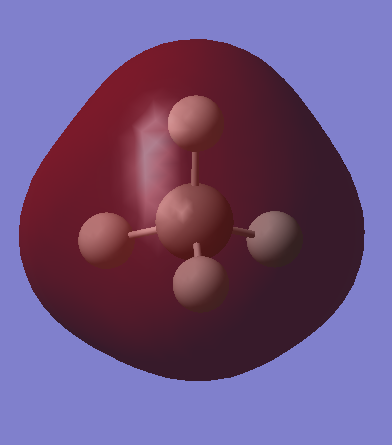
Carbon is negative and hydrogen is positive because of higher electronegativity of carbon.
1s atomic orbital of carbon contributes the MO. It is the core AOs so it is deep in energy(-10.16707 a.u.) so this is not very involved in the chemical bonding. MO is occupied.
This is a bonding MO of 2s orbital of carbon and 1s orbital of hydrogen. MO is occupied and this is a sigma bond.
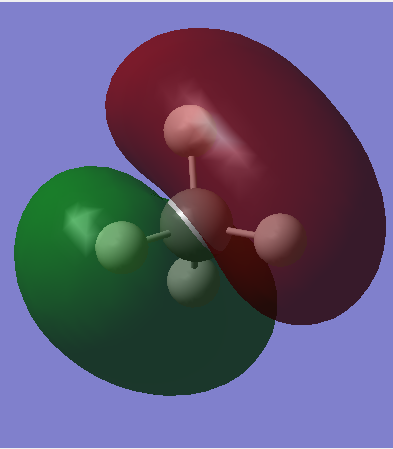
This is a sp3 hybridized orbital, and another 2 sp3 orbitals have different orientation, but they are all degenerate. The sp3 hybridized orbital is produced by combining 2p orbitals of carbon and the 1s orbital of hydrogen. It is MO bonding and occupied. This is also the HOMO. The energy is higher than the sigma bonding (shown in second picture), because of the better overlap of the orbitals.
This is MO anti-bonding combined by the 2s orbital of carbon and 1s orbital of hydrogen, which is the sigma anti-bonding of the second picture. This is the LUMO and unoccupied, so it is not involving in bonding.
This is one of the anti-bonding of the sp3 hybridized orbitals, which is the anti-bonding of the third picture. Another two anti-bonding orbital show different orientation. The anti-bonding is produced by combining the 2p orbital of carbon and the 1s orbital hydrogen out of phase. This orbital is high in energy. MO is not occupied so it is not involving in bonding.
CH4 + 2O2 -> CO2 + 2H2O (Further analysis)
The following part is illustrating the process to find the energy of the reaction. In order to find the energy of each molecule, oxygen, carbon dioxide and water molecules are optimized. The energy and optimizing results are shown in each section.
O2 molecule
Final energy E(RB3LYP): -150.25742434 a.u.
Item Value Threshold Converged?
Maximum Force 0.000130 0.000450 YES
RMS Force 0.000130 0.000300 YES
Maximum Displacement 0.000080 0.001800 YES
RMS Displacement 0.000113 0.001200 YES
Predicted change in Energy=-1.033738D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.216 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
O2 molecule |
The optimisation file is liked to here
CO2 molecule
Final energy E(RB3LYP): -188.58093945 a.u.
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000017 0.000300 YES
Maximum Displacement 0.000021 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Predicted change in Energy=-5.259645D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1691 -DE/DX = 0.0 !
! R2 R(1,3) 1.1691 -DE/DX = 0.0 !
! A1 L(2,1,3,-2,-1) 180.0 -DE/DX = 0.0 !
! A2 L(2,1,3,-3,-2) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
CO2 molecule |
The optimisation file is liked to here
H2O molecule
Final energy E(RB3LYP): -76.41973740 a.u.
Item Value Threshold Converged?
Maximum Force 0.000099 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000115 0.001800 YES
RMS Displacement 0.000120 0.001200 YES
Predicted change in Energy=-1.939668D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9652 -DE/DX = 0.0001 !
! R2 R(1,3) 0.9652 -DE/DX = 0.0001 !
! A1 A(2,1,3) 103.7454 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
H2O molecule |
The optimisation file is liked to here
Calculation
E(CH4)= -40.52401404 a.u. E(O2)= -150.25742434 a.u. 2*E(O2)= -300.5148487 a.u. E(CO2)= -188.58093945 a.u. E(H2O)= -76.41973740 a.u. 2*E(H2O)= -152.8394748 a.u. ΔE=[E(CO2)+2*E(H2O)]-[E(CH4)+2*E(O2)]= -0.38155151 a.u. =-1001.76 KJ/mol