Rep:Mod:XYZ2889
Optimizing the Reactants and Products
1,5-hexadiene
Anti-periplanar 4
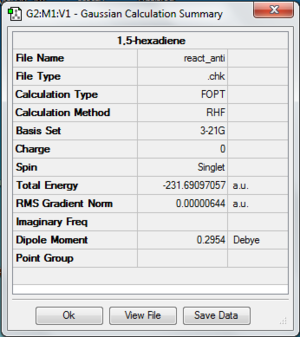
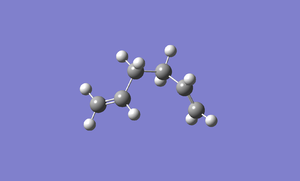
A molecule of 1,5-hexadiene with anti-periplanar conformation is drawn using Gaussview. First, the Job Type has to change to Optimisation. The molecule is calculated using Hartree Fock as a method and 3-21G as a basis set. Under the Link tab, the memory limit has to change to 250 MB and the calculation is submitted. The energy of the molecule for this conformation is -231.69097057 au. The point group is C1 and it has no symmetry. The molecule is exactly the same as Anti 4 in Appendix 1. File:React anti.chk

Gauche 3
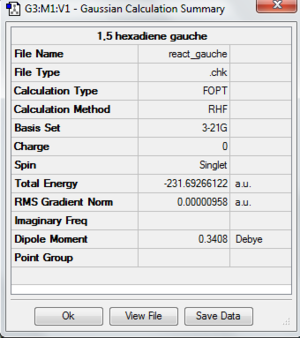
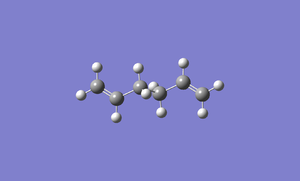
A molecule of 1,5-hexadiene with gauche conformation is drawn using Gaussview. The exact same calculation as above is carried out in this molecule. The method is still Hartree Fock and the basis set is still 3-21G. The energy for this conformation is -231.69266 au and the point group is C1 and it has no symmetry. The structure is exactly the same as Gauche 3 which is in Appendix 1. File:React gauche.chk
Based on the results above, we can clearly see that gauche conformation has the lowest energy conformation. However, it has not enough evidence to justify that all gauche conformation is lower in enery than anti-periplanar. There are still some of the gauche conformation which is higher in energy.
Anti-periplanar 2
A molecule of 1,5-hexadiene with the exact structure as anti-periplanar 2 is drawn using Gaussview. The structure is optimized by using HF/3-21G. It has a Ci symmetry with energy of -231.69253529 au. It has exactly the same energy with anti2 which is given in Appendix 1. File:React anti2.chk
The following is the summary of the calculation of the structure.
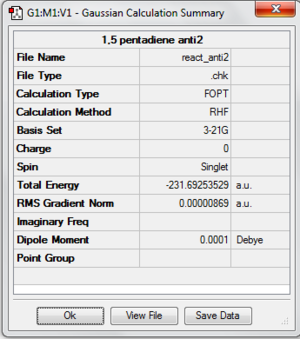
Now, the structure is re-optimized using DFT as the method and 6-31G(d)/6-31G* as the basis set. The energy of the optimized structure is -234.61171035 au. There is a difference in terms of energy between two different methods and basis set. File:React anti2.chk
The following is the summary of the calculation of the structure.
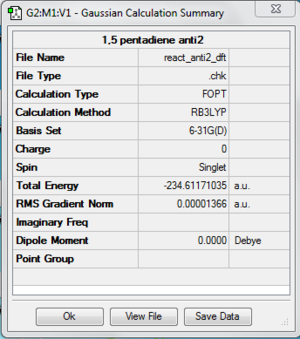
There is slight differences between two optimized structure. The overall structure seems like there is no difference but the bond length of C-H and C-C bond are slightly different. The overall energy of the two optimized structures are different, the energy of optimized structure using B3LYP/6-31* is higher than HF/3-21G.
| Basis set | C=C | C-C | C-H |
|---|---|---|---|
| HF/3-21G | 1.316 | 1.553 | 1.085 |
| B3LYP/6-31* | 1.334 | 1.548 | 1.098 |
Note that the bond distance of C-C and C-H bond are different in different places. The comparison that I have made is the one which is located at the same place. The bond length should be the same but due to difference between the methods and basis set that I have used, the bond length varied slightly.
Frequency Analysis
Using the optimized B3LYP/6-31G* structure, frequency analysis is carried out. First, Frequency is selected in the Job Type instead of optimization. Check the method is correctly input and submit the calculation. The frequencies mode and infrared spectrum can be seen by selecting Vibration under the Results tab. The following is the IR spectrum. File:React anti2 freq.chk
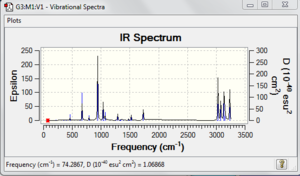
The following image shows the vibrational frequencies which do not have any imaginary frequency.
We can see the output file in the visualizer by clicking View File under Results tab. Under Thermodynamics section, we can see the sum of electronic and zero-point energies,sum of electronic and thermal energies, sum of electronic and thermal enthalpies and sum of electronic and thermal free energies. The first is the potential energy at 0 K including the zero-point vibrational energy. Second is the energy at 298.15 K and 1 atm of pressure which includes translational, rotational, and vibrational energy modes at this temperature. Third contains an additional correction for RT which is important if we are looking at dissociation reactions. The last one includes the entropic contribution to the free energy.
The following table is the list of energies I have extracted from output file.
Zero-point correction= 0.142507 (Hartree/Particle) Thermal correction to Energy= 0.149853 Thermal correction to Enthalpy= 0.150797 Thermal correction to Gibbs Free Energy= 0.110933 Sum of electronic and zero-point Energies= -234.469204 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500777
Optimizing the Chair and Boat Transition Structure
An allyl fragment(CH2CH2 is drawn and optimized using HF/3-21G basis set. A new window is opened and the optimized allyl fragment is copied and pasted twice in the new window. The two fragments are orientated in chair transition state and it is roughly 2.2 angstrom apart between the terminal ends.
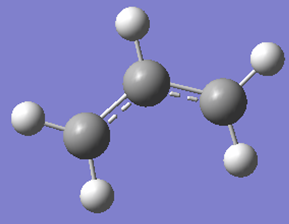
We are gong to optimize the transition structure manually. There are two ways of doing it, we can either guess the transition structure geometry or freeze the reaction coordinate molecule. For the first method, if the transition structure is too far from the exact structure, it will cause the curvature of the surface may be significantly different at points far removed from the transition structure. For the second method, it may not need to compute the whole Hessian once this has been done, and might give a good enough guess for the initial force constant matrix. This can save a considerable amount of time in cases where the force constant calculation is expensive.
Guess Transition Structure
Copy and paste the transition structure above to a new window. The structure can be optimized by change the Job Type into Opt+Freq and change Optimization to a Minimum to Optimization to a TS(Berny). The force constant is calculated once and "Opt=NoEigen" is typed into the additional keywords box. The keyword is to stop the calculation from crashing if more than one imaginary frequency is detected. The calculation is submitted and the following is the optimized transition structure.
There is one imaginary frequency (negative frequency) of magnitude 818 cm-1.
The following shows the vibration mode for the imaginary frequency.
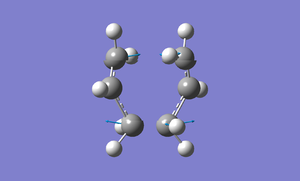
Freeze Reaction Coordinate Molecule
A new window is created and the optimized transition structure is copied and pasted into the new windows. Then in the Edit tab select the Redundant Coordinate Editor. A new coordinate is created and select two terminal carbon from allyl fragment which is formed or broken in the rearrangement. Select Bond instead of Unidentified and select Freeze Coordinate instead of Add. The structure is optimized and submitted for the calculation.
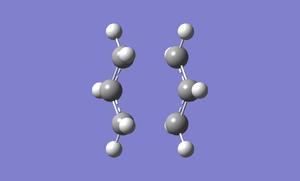
It looks like the structure above but without the bond distance being optimized. We then open the Redundant Coordinate Editor and do the same thing as above except we select Derivatives instead of Add. The structure is optimized and submitted for the calculation.

The bond length of the bond forming and bond breaking C-C bond is about the same (for the guess transition structure is 2.02035 angstrom and for the freeze coordinate method is 2.02122 angstrom.)for both the structure by using different methods to predict the transition structure. Both the structures are exactly the same.
Boat Transition
The optimized Ci reactant molecule is opened and copied into a new window. Select the Add to MolGroup from the New tab and the structure will be disappeared. Copy and paste the structure for the second time and click on the icon showing two molecule side by side, both the molecules will show simultaneously. Orientate the molecules and renumber all the atoms by going to Edit and clicking on the Atom List. The atom number must be the same as in the manual given. After that, QST2 calculation should set up. In the Job Type tab, Opt+Freq is selected. Then, select TS(QST2) and submit the job. It didn't work. When the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not even consider the possibility of a rotation around the central bonds. That's why the structure looked a bit like the chair transition structure.
We can modify the dihedral angle C-C-C-C to 00 and the angle C-C-C to 1000 for both the molecules. Submit the calculation again.
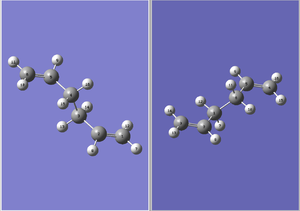
There is only one imaginary frequency and the vibration of that imaginary frequency is Cope rearrangement. It is shown in the image below.
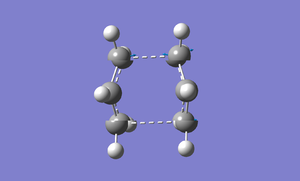
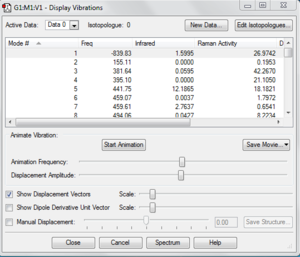
In order to predict the which conformer the reaction paths from the transitions structures will lead to, we have to use IRC method (Intrinsic Reaction Coordinate) which can allows us to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. First, open the chk file of the optimized chair transition structure. We calculate using IRC as the Job Type. Since the reaction coordinate is symmetrical, we just select the forward reaction to compute. We also need to calculate the force constant but only for once. Then we will put in 50 number of points for along the IRC and submit the calculation.
The intermediate geometry has not reached a minimum geometry yet. Then, I take the last point on the IRC and run the minimization. This is the structure I got.

I repeated the same thing for the boat structure.

Comparing Chair and Boat Transition Structure
Both the Chair and Boat transition structures are optimized at HF/3-21G basis set first followed by B3LYP/6-31G* using frequency calculation. Then we can compare the difference in the energies between the reactants and transition states at the two levels of theory.
Reactant(HF/3-21G) File:REACT ANTI2 FREQ1.LOG File:REACT ANTI2 FREQ1.chk
Zero-point correction= 0.151918 (Hartree/Particle) Thermal correction to Energy= 0.158187 Thermal correction to Enthalpy= 0.159131 Thermal correction to Gibbs Free Energy= 0.122103 Sum of electronic and zero-point Energies= -231.538321 Sum of electronic and thermal Energies= -231.532052 Sum of electronic and thermal Enthalpies= -231.531108 Sum of electronic and thermal Free Energies= -231.568135
Reactant(B3LYP/6-31G*) File:REACT ANTI2 FREQ.LOG File:React anti2 freq.chk
Zero-point correction= 0.142507 (Hartree/Particle) Thermal correction to Energy= 0.149853 Thermal correction to Enthalpy= 0.150797 Thermal correction to Gibbs Free Energy= 0.110933 Sum of electronic and zero-point Energies= -234.469204 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500777
Boat(HF/3-21G) File:BOAT GUESS 321G.LOG File:Boat guess 321g.chk
Zero-point correction= 0.151872 (Hartree/Particle) Thermal correction to Energy= 0.157503 Thermal correction to Enthalpy= 0.158447 Thermal correction to Gibbs Free Energy= 0.123025 Sum of electronic and zero-point Energies= -231.450930 Sum of electronic and thermal Energies= -231.445300 Sum of electronic and thermal Enthalpies= -231.444355 Sum of electronic and thermal Free Energies= -231.479777
Boat(B3LYP/6-31G*) File:BOAT GUESS 631G 1.LOG File:Boat guess 631g 1.chk
Zero-point correction= 0.141957 (Hartree/Particle) Thermal correction to Energy= 0.147885 Thermal correction to Enthalpy= 0.148829 Thermal correction to Gibbs Free Energy= 0.113129 Sum of electronic and zero-point Energies= -234.398519 Sum of electronic and thermal Energies= -234.392591 Sum of electronic and thermal Enthalpies= -234.391647 Sum of electronic and thermal Free Energies= -234.427347
Chair(B3LYP/6-31G*) File:CHAIR TS GUESS2A 321G 1.LOG File:CHAIR TS GUESS2A 321G 1a.chk
Zero-point correction= 0.142834 (Hartree/Particle) Thermal correction to Energy= 0.149296 Thermal correction to Enthalpy= 0.150240 Thermal correction to Gibbs Free Energy= 0.113201 Sum of electronic and zero-point Energies= -234.411624 Sum of electronic and thermal Energies= -234.405162 Sum of electronic and thermal Enthalpies= -234.404218 Sum of electronic and thermal Free Energies= -234.441257
Chair(HF/3-21G) File:CHAIR TS GUESS2A 321G.LOG File:Chair ts guess1 321g.chk
Zero-point correction= 0.152618 (Hartree/Particle) Thermal correction to Energy= 0.157978 Thermal correction to Enthalpy= 0.158922 Thermal correction to Gibbs Free Energy= 0.124111 Sum of electronic and zero-point Energies= -231.466704 Sum of electronic and thermal Energies= -231.461344 Sum of electronic and thermal Enthalpies= -231.460400 Sum of electronic and thermal Free Energies= -231.495211
| Conformation | Electronic energy (HF/3-21G) | Sum of electronic and zero-point energies(HF/3-21G) | Sum of electronic and thermal energies(HF/3-21G) | Electronic energy(B3LYP/6-31G*) | Sum of electronic and zero-point energies(B3LYP/6-31G*) | Sum of electronic and thermal energies(B3LYP/6-31G*) |
|---|---|---|---|---|---|---|
| Chair(TS) | -231.618618 | -231.466704 | -231.461344 | -234.554458 | -234.411624 | -234.405162 |
| Boat(TS) | -231.602802 | -231.450930 | -231.445300 | -234.546404 | -234.398519 | -234.392591 |
| Reactant(anti2) | -231.690239 | -231.538321 | -231.532052 | -234.611711 | -234.469204 | -234.461857 |
| ΔE | HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Exp |
|---|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | 0K | |
| ΔE (Chair) | 44.87 | 44.37 | 36.13 | 35.58 | 33.5 ± 0.5 |
| ΔE (Boat) | 54.77 | 54.44 | 44.36 | 43.67 | 44.7 ± 2.0 |
Diels Alder Cycloaddition
The Diels Alder reaction belongs to pericyclic reactions. The π orbitals of the dieneophile overlaps and form new σ bonds with the π orbitals of the diene. Number of π electrons involved affect the likelihood of the reaction to occur. Based on MO theory, HOMO/LUMO of one reactant interacts with HOMO/LUMO of the other reactants to form two new bonding and anti-bonding MOs.
Butadiene
A cis butadiene is built in Gaussview and is optimized using AM1 semi-empirical molecular orbital method. The following image is the optimized cis butadiene. File:Butadiene am1.chk
Then, we use Gaussview to plot the HOMO and LUMO of cis-butadiene. In the edit tab, click on MOs. Click on the visualize tab and click HOMO/LUMO. The HOMO/LUMO will appear after clicking the update button. The two images below are the HOMO and LUMO of cis-butadiene.


The following image is the plot of HOMO an LUMO of butadiene.

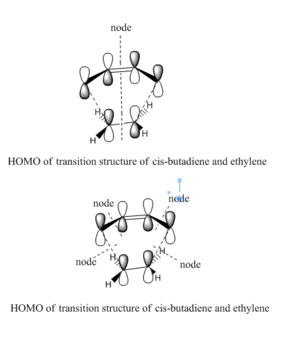
From the diagram above, it is clear that the HOMO of butadiene is asymmetry and the LUMO of butadiene is symmetry.
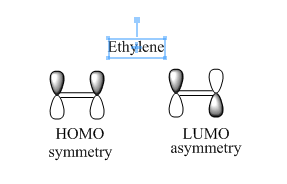
The diagram above shows that HOMO of ethylene is symmetry and LUMO of ethylene is asymmetry.
Transition Structure of Reaction between Butadiene and Ethylene
Transition structure of the reaction between butadiene and ethylene is built in Gaussview. The interfragment distance is guessed. The following shows the image of transition structure before optimized.
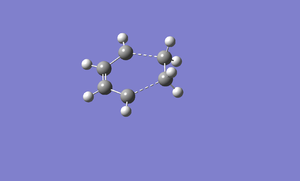
The transition structure is optimized using AM1 semi-empirical molecular orbital. Below is the image of optimized transition structure. File:Cycloaddition a1.chk

The dashed line is the bond forming/bond breaking.
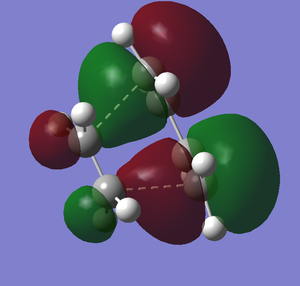
The HOMO and LUMO of the transition structure can be obtained as the way I have described above. Below are the images of HOMO and LUMO of transition structure.

In sp3 C-C bond length is 154 pm. In sp2 C=C bond length is 134 pm. The Van der Waals radius of carbon atom is 170 pm. The bond length of C-C bond in transition structure is 2.31 angstrom which is shown below:

From the results I get, the C-C bond in the transition structure is longer than usual sigma and pi bond. Therefore, C-C bond is partly formed sigma bond but it is repulsed by the Van der Waals radius of carbon.
The following image is the plot of HOMO an LUMO of transition structure.
From the diagram above,we can clearly see that the HOMO of the transition structure is asymmetry and the LUMO of the transition structure is symmetry. For the HOMO of transition structure, butadiene uses LUMO of its MO and ethylene uses HOMO. This is shown very clearly in the previous section. This cycloaddition is allowed because HOMO of one of the reactants which is ethylene interacts with LUMO of the other reactants which is butadiene to form MO. Therefore the cycloaddition can occur.
The image below shows the vibration that corresponds to the reaction path at the transition state. It shows that the bond formation is asynchronous. The vibrational frequency is 537.10cm-1. The lowest positive frequency which is 74.26 cm-1 has a very different vibration from the vibration of reaction path. The ethylene vibrates in a higher magnitude than butadiene. The bonds between ethylene and butadiene do not vibrate much.


Transition Structure of Reaction between Cyclohexa-1,3-diene and Maleic Anhydride
Exothermic Product
A rough transition structure of an exothermic product is built and optimized by using AM1/semi-empirical molecular orbital method. I used the freezing coordination method to get the transition structure. File:DIELSALDER GUESS EXO 1.LOG
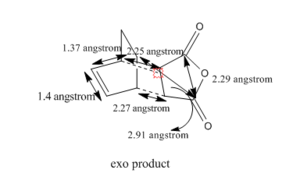
The bond length of C-C bond are 2.25 angstrom and 2.27 angstrom[1]. The diagram below shows the various bond length of C-C bond.
The HOMO and LUMO of the transition structure is shown below using Gaussview.
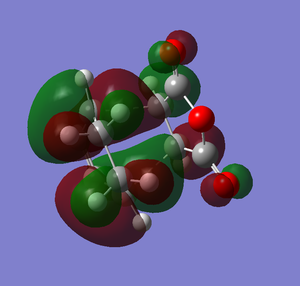
Endothermic Product
A rough transition structure of an endothermic product is built and optimized by using AM1/semi-empirical molecular orbital method. I used the freezing coordination method to get the transition structure. The following is the transition structure. File:DIELSALDER GUESS ENDO 1.LOG

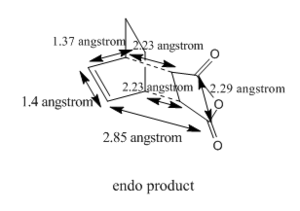
The bond length of C-C bonds are 2.23110 angstrom and 2.23095 angstrom[1]. The diagram below shows the bond length of various C-C bond.
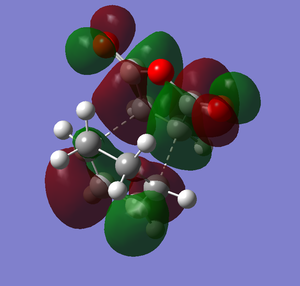
HOMO and LUMO of the transition structure can be illustrated by using Gaussview and the following images are HOMO and LUMO of the transition structure.

Comparing Endothermic and Exothermic Product
There is a huge structural difference between exo and endo products. For the exo product, the five membered ring is located at the equatorial position. For the endo product, the five membered ring is located at the axial position. We found out that the exo form is more strained. It is based on the spacial bond length between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2-. The bond length is 2.91 angstrom. If we compare with endo form, the bond length between the “opposite” -CH=CH- for the endo and the -(C=O)-O-(C=O)- fragment of the maleic anhydride is 2.85 angstrom. We can say that exo formed experience more steri repulsion than endo formed so it has higher bond length.
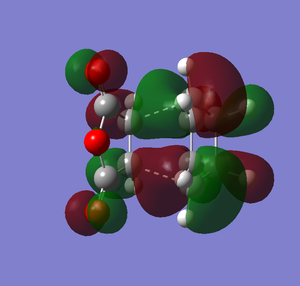
The overall energy for the exothermic product is -605.6035 au. The overall energy for endothermic product is -605.61037 au. The overall energy of the exothermic product is higher than the overall energy of the endothermic product. The difference of both products in overall energy is 0.00687 au which is 4.31 kcal/mol(0.00687*627.51). Therefore exothermic product is less stable than the endothermic product. Why is that the case? Let's look at the HOMO of both products. Below are the drawings of the HOMO of both products with the overlap orbitals based on the HOMO I have obtained in the previous section.
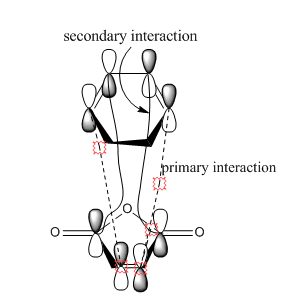
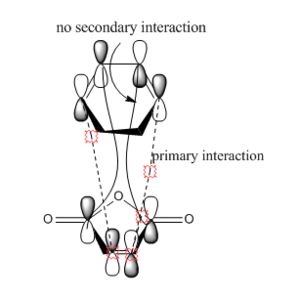
Based on the images above, we can see that in the endo product there is the primary interaction between two orbitals which links to bond formation. There is also another interaction that is formed in endo product that is the secondary interaction. The secondary interaction does not lead to the bond formation but it can stabilize the compound cause the energy of the transition state to be lower.[2] For exo product, there is no secondary interaction between orbitals so it cannot stabilize the transition state. Therefore, the activation energy will be lower and thus endo product is more favored. The overall effect of the secondary orbital is called secondary orbital effect
Further Discussion
For the Diels-Alder reaction, I have neglected the delocalisation of electrons in maleic anhydride in the reaction of cyclohexa-1,3-diene and maleic anhydride. The delocalisation of electrons in maleic anhydride will reduce the electron density on the carbon double bond because of the strong electronegativity and electron withdraing group of the oxygen atoms. This causes the pi* orbital to be higher. This will cause some difference in the overlap of molecular orbitals.
Reference
The bond length of C-C bonds are 2.23110 angstrom and 2.23095 angstrom[1]
The bond length of C-C bond are 2.25 angstrom and 2.27 angstrom[1]
- ↑ John McMurry, Organice Chemistry 7th edition, 2008, 1-35
here is also another interaction that is formed in endo product that is the secondary interaction. The secondary interaction does not lead to the bond formation but it can stabilize the compound cause the energy of the transition state to be lower.[1]
- ↑ Ian Fleming, Frontier Orbitals and Organice Chemical Reactions,1976, 106-107
