Rep:Mod:XYZ271995
Haber Process
Ammonia is a colourless gas with a characteristic pungent smell. It is extensively used as fertilizers. Industrially, ammonia is synthesized by reacting nitrogen and hydrogen in presence of iron catalyst.

NH3
This section would further discuss the results of computational modelling of an ammonia molecule using Gaussian software. The molecule has been optimized and its bond length, bond angle, energy, point group and vibrational modes are reported below.
| Ammonia (NH3) | |||||
|---|---|---|---|---|---|
| |||||
| More Info | |||||
| Name | Ammonia (NH3) | ||||
| N-H Bond Length | 1.01798 Å | ||||
| H-N-H Bond Angle | 105.741o | ||||
| Final energy E (RB3LYP) | -56.55776873 atomic units | ||||
| RMS gradient | 0.00000485 atomic units | ||||
| Point Group | C3v | ||||
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986289D-10
Optimization completed.
-- Stationary point found.

The molecule is nitrogen trihydride, or more commonly known as ammonia. Molecule is optimized using Gaussian 5.0.9. Optimization is carried out by:
- Method: B3LYP
- The basis set: 6-31G(d,p)
- and type of calculation to do: OPTF (optimise and frequency analysis)
IR Vibrations
From the 3N-6 rule, ammonia is expected to have 6 vibrational modes:
- There are 2 pairs of degenerate vibrational modes: mode 2 and 3; and mode 5 and 6
- Mode 1, 2 and 3 are "bending" vibrations and Mode 4, 5 and 5 are bond stretching vibrations.
- Mode 4 is highly symmetric.
- Mode 1 is known as the "umbrella" mode.
- In IR absorption for gaseous ammonia, 1 strong band and 1 weak band are expected, which are corresponding to Mode 1 and degenerate pair (Mode 2 and 3), respectively. Modes 4, 5 and 6 are expected to be too weak and might be indistinct from background noise.
Charge
- Charge on N atom in Ammonia is calculated to be -1.125 using Gaussian and Charge on H atom in Ammonia is calculated to be 0.375 using Gaussian. Nitrogen is much more electronegative than hydrogen atoms, which is consistent with the simulation: nitrogen atom is negatively charged while hydrogen atoms are positively charged.
Additional Link
This is a link to the LOG file for the Optimized Ammonia Molecule
Nitrogen
This section would further discuss the results of computational modelling of a nitrogen molecule using Gaussian software. The molecule has been optimized and its bond length, bond angle, energy, point group and vibrational modes are reported below.
| Nitrogen (N2) | |||||
|---|---|---|---|---|---|
| |||||
| More Info | |||||
| Name | Nitrogen(N2) | ||||
| N≡N Bond Length | 1.10550 Å | ||||
| N≡N Bond Angle | 180o | ||||
| Final energy E (RB3LYP) | -109.52412868 atomic units | ||||
| RMS gradient | 0.00000060 atomic units | ||||
| Point Group | D∞h | ||||
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401074D-13
Optimization completed.
-- Stationary point found.

The molecule is Nitrogen. Molecule is optimized using Gaussian 5.0.9. Optimization is carried out by:
- Method: B3LYP
- The basis set: 6-31G(d,p)
- and type of calculation to do: OPTF (optimise and frequency analysis)
IR Vibrations
From the 3N-5 rule, nitrogen is expected to have 1 vibrational mode.
- In IR absorption for gaseous nitrogen, no peak is expected because it is IR inactive (no change in dipole moment after absorbing IR radiation).
Charge
- Charge on N atom in Nitrogen is calculated to be 0 using Gaussian. The two molecules have the same electronegativity. Hence, the N≡N Bond is a pure covalent bond with zero ionic character (consistent with simulation: 0 net charge).
Additional Link
This is a link to the LOG file for the Optimized Nitrogen Molecule
Hydrogen
This section would further discuss the results of computational modelling of a hydrogen molecule using Gaussian software. The molecule has been optimized and its bond length, bond angle, energy, point group and vibrational modes are reported below.
| Hydrogen (H2) | |||||
|---|---|---|---|---|---|
| |||||
| More Info | |||||
| Name | Hydrogen(H2) | ||||
| H-H Bond Length | 0.74279 Å | ||||
| H-H Bond Angle | 180o | ||||
| Final energy E (RB3LYP) | -1.17853936 atomic units | ||||
| RMS gradient | 0.00000017 atomic units | ||||
| Point Group | D∞h | ||||
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
The molecule is Hydrogen. Molecule is optimized using Gaussian 5.0.9. Optimization is carried out by:
- Method: B3LYP
- The basis set: 6-31G(d,p)
- and type of calculation to do: OPTF (optimise and frequency analysis)
IR Vibrations
From the 3N-5 rule, hydrogen is expected to have 1 vibrational mode.
- In IR absorption for gaseous hydrogen, no peak is expected because it is IR inactive (no change in dipole moment after absorbing IR radiation).
Charge
- Charge on H atom in Hydrogen is calculated to be 0 using Gaussian. The two molecules have the same electronegativity. Hence, the H-H Bond is a pure covalent bond with zero ionic character (consistent with simulation: 0 net charge).
Additional Link
This is a link to the LOG file for the Optimized Hydrogen Molecule
Hess Law
Hess' Law states that regardless of the multiple stages or steps of a reaction, the total enthalpy change for the reaction is the sum of all individual enthalpy involved. Using Hess Law, it is then possible to calculate the enthalpy of reaction:
| Energy of Reaction | ||
|---|---|---|
| E(NH3)= | -56.55776873 atomic units | |
| 2*E(NH3) | -113.11553746 atomic units | |
| E(N2) | -109.52412868 atomic units | |
| E(H2) | -1.17853936 atomic units | |
| 3*E(H2) | -3.53561808 atomic units | |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.0557907 atomic units = -146.5 kJ mol-1 | |
Gaseous nitrogen has the most negative potential energy (-109.5 atomic units) as compared to gaseous ammonia (-56.5 atomic units) and hydrogen(-1.18 atomic units), which means nitrogen is most stable amongst the three in their gaseous forms. However, when we observe the stoichiometric reaction as a whole, the sum of energy in ammonia molecules is less than sum of energy in gaseous nitrogen and hydrogen. Consequently, conversion of nitrogen and hydrogen to ammonia is thermodynamically favourable.
Literature value for the standard enthalpy of formation of ammonia is -9.34 kcal/mol.[1] When converted to enthalpy change of reaction in Haber process, it is equivalent to -78.1 kJ mol-1. This shows the inadequacy of using simple DFT methods to calculate thermodynamic data.
BH3
This section would further discuss the results of computational modelling of a borane molecule using Gaussian software. The molecule has been optimized and its bond length, bond angle, energy, point group and vibrational modes are reported below.
| Borane (BH3) | |||||
|---|---|---|---|---|---|
| |||||
| More Info | |||||
| Name | Borane (BH3) | ||||
| B-H Bond Length | 1.19232 Å | ||||
| H-B-H Bond Angle | 120o | ||||
| Final energy E (RB3LYP) | -26.61532364 atomic units | ||||
| RMS gradient | 0.00000211 atomic units | ||||
| Point Group | D3h | ||||
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000017 0.001800 YES
RMS Displacement 0.000011 0.001200 YES
Predicted change in Energy=-1.053682D-10
Optimization completed.
-- Stationary point found.

The molecule is boron trihydride, or more commonly known as borane. Molecule is optimized using Gaussian 5.0.9. Optimization is carried out by:
- Method: B3LYP
- The basis set: 6-31G(d,p)
- and type of calculation to do: OPTF (optimise and frequency analysis)
IR Vibrations
From the 3N-6 rule, borane is expected to have 6 vibrational modes:
- There are 2 pairs of degenerate vibrational modes: mode 2 and 3; and mode 5 and 6
- Mode 1, 2 and 3 are "bending" vibrations and Mode 4, 5 and 5 are bond stretching vibrations.
- Mode 4 is highly symmetric. Furthermore, mode 4 is IR inactive because there is no change in dipole moment for that particular bond stretching after the molecule absorbs IR radiation/
- Mode 1 is known as the "umbrella" mode.
- In IR absorption for gaseous borane, 2 strong bands and 1 weak band are expected, which are corresponding to Mode 1 and degenerate pair (Mode 5 and 6) and the other degenerate pair (Modes 2 and 3) respectively. Mode 4 is IR silent.
Charge
- Charge on B atom in Borane is calculated to be 0.297 using Gaussian and Charge on H atom in Borane is calculated to be -0.099 using Gaussian. Hydrogen atoms are relatively more electronegative than Boron atom, which is consistent with simulation: they are slightly negatively charged while and Boron atom is positively charged.
Additional Link
This is a link to the LOG file for the Optimized Borane Molecule
Simulated Molecular Orbitals

| Number | Shape of MO | Description |
| 1 | 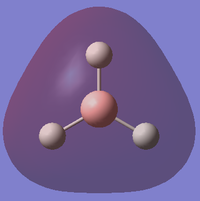
|
This is a model of a filled 2σ molecular orbital in BH3 (E=-0.51254). It is formed by in-phase head-on overlap between 2s atomic orbital in Boron atom and 1s orbital in one of the 3 Hydrogen atoms. |
| 2 | 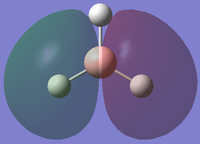
|
This is a model of a filled 3σ molecular orbital in BH3 (E=-0.35079). It is formed by in-phase head-on overlap between 2p atomic orbital in Boron atom and 1s orbital in one of the 3 Hydrogen atoms. |
| 3 | 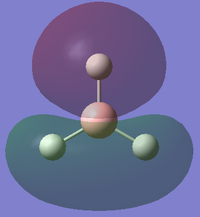
|
This is a model of a filled 4σ molecular orbital in BH3 (E=-0.35079). It is on the same energy level as the 3σ molecular orbital (degenerate orbitals). It is formed by in-phase head-on overlap between 2p atomic orbital in Boron atom and 1s orbital in one of the 3 Hydrogen atoms. |
| 4 | 
|
This is a model of a non-filled 2p atomic orbital in BH3 (E=-0.06605). This molecular orbital is of particular interest because this is the Lowest Unoccupied Molecular Orbital (LUMO) in BH3. BH3 is known to be highly reactive because it does not have an octet structure. BH3 is known to act as a Lewis acid and it reacts with NH3 (Lewis base) to form ammonia borane. However, the BH3 molecule needs to absorb energy in order to distort from D3h to C3v symmetry, so that its LUMO orbital will have the same symmetry as the HOMO orbital of NH3. This will allow the LUMO and HOMO orbitals to combine linearly to form two new molecular orbitals thereby forming the adduct.[3] |
| 5 | 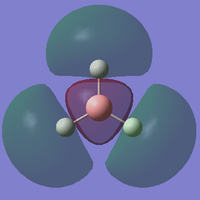
|
This is a model of a non-filled 6σ* molecular orbital in BH3 (E=0.16839). It is formed by out-of-phase head-on overlap between 2p atomic orbital in Boron atom and 1s orbital in one of the 3 Hydrogen atoms. |
References
- ↑ Petersson, G. A., and John Mantzaris. "Calculated heat of formation of ammonia." J. Am. Chem. Soc 113.7 (1991): 2486-2490. Print.
- ↑ Baibich, Ione M., and Ian S. Butler. "A brief introduction to molecular orbital theory of simple polyatomic molecules for undergraduate chemistry students." Química Nova 35.7 (2012): 1474-1476. Print.
- ↑ Baibich, Ione M., and Ian S. Butler. "A brief introduction to molecular orbital theory of simple polyatomic molecules for undergraduate chemistry students." Química Nova 35.7 (2012): 1474-1476. Print.
