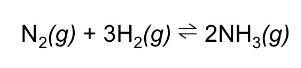Rep:Mod:XYZ1235
NH3 Optimization in Gaussian

Link to the LOG file = link
Molecule Name = Ammonia or Azane
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy = - 56.55776873 a.u.
Point Group = C3V
Bond Lenghts = 101.811 pm
Bond Angle = 105.70713°
The optimization gave results close to the literature values:
Literature value 101.2 pm N-H.[1]
Literature value 106.7° H–N–H.[2]
ITEM TABLE
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986287D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A good optimization give us the structure with the lowest energy possible. The force in the item table is the first derivative of the potential curve whose minimum point describes the point of maximum stability for the molecule. Therefore, the closer the force is to zero, the better the optimization is.
Jmol Image
NH3 |
Display Vibration



Number of modes expected
As expected by the 3N-6 rule, the molecule presents 6 vibrational modes.
Degenerate modes
The degenerate modes are 2 and 3(stretching), 5 and 6 (bending).
Bending Vibrations
The bending vibrations are 1, 2 and 3.
Stretching Vibrations
The stretching vibrations are 4, 5 and 6.
Highly symmetric modes
The highly symmetric modes are 1 (stretching) and 4 (bending).
Umbrella mode = 1
IR Spectrum
The molecule is expected to show four IR peaks with different heights due to degeneracy of vibrational modes. The shortest peak represent the stretching vibration 1, while the second one represents the vibrations 2 and 3. The two peaks for vibrations 4 and 5 and 6(last two would appear as a single peak due to degeneracy), are not evident because of the small size of the amplitude. The intensity of the peaks depend on the change of dipole moment of the molecule. For vibrations 1,2 and 3, the dipole moment changes significantly, while for 4, 5 and 6 the change is so slight the amplitude is not visible in the spectrum. The frequency of vibration is proportional to the bond strength and inversely proportional to the reduced mass of the system.
Charges
The Nitrogen is more electronegative, meaning that the electron density will tend to be away from the Hydrogen atom.The sum of all the atomic charges is equal to zero, giving an overall neutral molecule.
H2 Optimization in Gaussian
Link to the LOG file = link
Molecule Name = Hydrogen Molecule
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy = - 1.17853935 a.u.
Point Group = D∞h
Bond Lenghts = 0.7427 A
Bond Angle = 180°
The optimization gave results close to the literature values:
Literature value 0.74 A H-H.[3]
ITEM TABLE
Item Value Threshold Converged?
Maximum Force 0.000048 0.000450 YES
RMS Force 0.000048 0.000300 YES
Maximum Displacement 0.000063 0.001800 YES
RMS Displacement 0.000089 0.001200 YES
Predicted change in Energy=-2.989263D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7427 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A good optimization give us the structure with the lowest energy possible. The force in the item table is the first derivative of the potential curve whose minimum point describes the point of maximum stability for the molecule. Therefore, the closer the force is to zero, the better the optimization is.
Jmol Image
H2 |
Display Vibrations


Number of modes expected
As expected from the 3N-5 rule for linear molecule, hydrogen shows one stretching mode.
Degenerate modes = None
Bending Vibrations = None
Stretching Vibrations = 1
Highly symmetric modes = 1
Umbrella mode = None
IR Spectrum
The graph only shows one peak because there is only one vibrational mode. The intensity of the peak is zero because there is no change in dipole moment. The frequency of vibration is directly proportional to the bond strength and inversely proportional to the reduced mass of the system.
Charges
Both the hydrogen atoms have the same electronegativity, meaning that the charge will be equally distributed and the molecule will be overall neutral.
N2 Optimization in Gaussian

Link to the LOG file = link
Molecule Name = Nitrogen molecule
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy = - 109.52412867 a.u.
Point Group = D∞h
Bond Lenghts = 1.10550 A
Bond Angle = 180°
The optimization gave results close to the literature values:
Literature value 1.0975 A N-N.[4]
ITEM TABLE
Item Value Threshold Converged?
Maximum Force 0.000054 0.000450 YES
RMS Force 0.000054 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000024 0.001200 YES
Predicted change in Energy=-9.040444D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A good optimization give us the structure with the lowest energy possible. The force in the item table is the first derivative of the potential curve whose minimum point describes the point of maximum stability for the molecule. Therefore, the closer the force is to zero, the better the optimization is.
Jmol Image
N2 |
Display Vibrations



Number of modes expected
As expected from the 3N-5 rule for linear molecule, nitrogen shows one stretching mode.
Degenerate modes = None
Bending Vibrations = None
Stretching Vibrations = 1
Highly symmetric modes = 1
Umbrella mode = None
IR Spectrum
The graph only shows one peak because there is only one vibrational mode. The intensity of the peak is zero because there is no change in dipole moment. The frequency of vibration is lower than the hydrogen molecule one. This is because even if the triple Nitrogen bond is stronger than the single Hydrogen one, the mass of Nitrogen is much bigger than Hydrogen. The N2 stretching frequency respect the literature values as it should be around the 2200 cm-1 region.
Charges
Both the nitrogen atoms have the same electronegativity, meaning that the charge is equally distributed and the molecule is overall neutral.
Energy in the synthesis of Ammonia
The ammonia product has a lower energy than the reactants.
ΔE = 2*E(NH3)-[E(N2)+3*E(H2)]= 0.055 a.u =
= - 144.4025 KJ/mol
| Energy of products (negative) | Energy of reactants (negative) |
|---|---|
| 113.06 a.u | 113.12 a.u. |
| 296839.03 KJ/mol | 296996.56 KJ/mol |
= (-56.55776873)*2 - (-109.52412867 + 3*(- 1.17853935))
= - 0.055 a.u.
ΔE = - 0.055 * 2625.5 = - 144.4025 KJ/mol
The reaction, also known as Haber process, is an exothermic. The literature value for the change in Enthalpy is ΔH° = −92 kJ·mol-1.[5] The literature value is smaller than the one obtained with the optimization. This might be due to the fact that our value is obtained by summing up individual bond energies singularly, while in reality breaking a bond affect the rest of the molecule as well.
Molecule of Choice Analysis
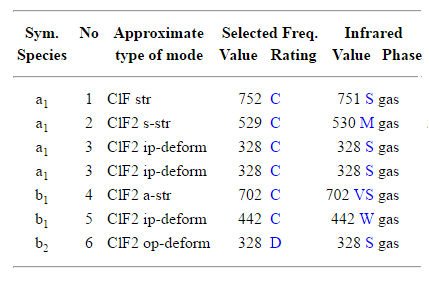
ClF3 Optimization in Gaussian

Link to the LOG file = link
Molecule Name = Chlorine Trifluoride
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
Final Energy = - 759.46531688 a.u.
Point Group = C2v
Bond Lenghts = two Cl-F bonds of 1.72863 A and one of 1.65143 A.
Bond Angle = two angles of 87.14037° and one of 174.28073°.
The optimization gave results close to the literature values:
Literature values: two bond lenghts of 1.588 A (Cl-F) and one of 1.698 A.[6]
Literature values: two angles of 87.5° and one of 175°.[7]
ITEM TABLE
Item Value Threshold Converged?
Maximum Force 0.000050 0.000450 YES
RMS Force 0.000028 0.000300 YES
Maximum Displacement 0.000222 0.001800 YES
RMS Displacement 0.000134 0.001200 YES
Predicted change in Energy=-1.250225D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.7286 -DE/DX = 0.0 !
! R2 R(1,3) 1.7286 -DE/DX = 0.0 !
! R3 R(1,4) 1.6514 -DE/DX = 0.0 !
! A1 A(2,1,4) 87.1404 -DE/DX = 0.0 !
! A2 A(3,1,4) 87.1404 -DE/DX = 0.0 !
! A3 L(2,1,3,4,-1) 174.2807 -DE/DX = 0.0 !
! A4 L(2,1,3,4,-2) 180.0 -DE/DX = 0.0 !
! D1 D(1,2,4,3) 0.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
A good optimization give us the structure with the lowest energy possible. The force in the item table is the first derivative of the potential curve whose minimum point describes the point of maximum stability for the molecule. Therefore, the closer the force is to zero, the better the optimization is.
Jmol Image
ClF3 |
Display Vibration



Number of modes expected
As expected from the 3N-6 rule for non linear molecule, Chlorine Trifluoride shows 6 vibrational modes.
Degenerate modes = None
Bending Vibrations = 1, 2 and 3
Stretching Vibrations = 4, 5 and 6
Highly symmetric modes = None
Umbrella mode = None
IR Spectrum
The spectrum is expected to show 6 different peaks, but only 3 of them are evident due to inhomogeneous broadening. Vibrations 3 and 4 present amplitudes too small to be seen in the spectrum (due to a slight change in the dipole moment of the molecule), while vibrations 1 and 2 appear as a unique peak due to the fact that their frequencies of vibrations are very close to each others. Vibrations 5 and 6 are clearly distinguishable on the right of the spectrum.
The frequency of vibration are similiar to the literature values.[8]
Charges
Fluorine is the most electronegative element in the periodic table and attracts electron density away from the central Chlorine atom. The single atomic charges sum up to zero to give a neutral molecule.
Molecular Orbital Analysis
1.MO given by the overlap of s orbitals all in phase with each others. The electron density is localized along the bond axis, giving the bond a sigma character. The orbital is occupied and has a relatively low energy.
2.MO given by the overlap of s orbitals. The Fluorine s orbitals are all in phase with each others, but not in phase with the Chlorine one. The electron density is localized along the bond axis, giving the bond a sigma anti-bonding character. The orbital is occupied and is higher in energy than the corresponding sigma orbital.
3.MO given by the overlap of Chlorine and Fluorine pz orbitals all in phase with each others. The orbital symmetry of the bond is the same as that of the p orbital when seen down the bond axis, giving the bond a pi bond character. The orbital is occupied and is higher in energy than the the sigma anti-bonding orbital.
4.MO given by the overlap of Chlorine and Fluorine pz orbitals not phase with each others. The orbital symmetry of the bond is the same as that of the p orbital when seen down the bond axis, giving the bond a pi bond character. The orbital is occupied and is higher in energy than the the corresponding pi bonding orbital.
5.MO given by the overlap of Cholrine and Fluorine s orbitals. Two of the Fluorine orbitals are in phase with the Chlorine, but the third one is out of phase, adding anti-bonding contribution to the bond. This is why it is higher in energy than the sigma bond molecular orbital.
References
- ↑ CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-26. Retrieved 18 June 2013.
- ↑ CRC Handbook of Chemistry and Physics, 94th ed. http://www.hbcpnetbase.com. Page 9-26. Retrieved 18 June 2013.
- ↑ Roger L. DeKock; Harry B. Gray; Harry B. Gray (1989). Chemical structure and bonding. University Science Books. p. 199. ISBN 0-935702-61-X.
- ↑ Tables of Interatomic Distances and Configuration in Molecules and Ions, L.E. Sutton, ed., London: The Chemical Society, 1958
- ↑ Appl, Max (2005), "Ammonia", Ullmann's Encyclopedia of Industrial Chemistry, Weinheim: Wiley-VCH
- ↑ Smith, D. F. (1953). "The Microwave Spectrum and Structure of Chlorine Trifluoride". The Journal of Chemical Physics. 21 (4): 609–614. Bibcode:1953JChPh..21..609S
- ↑ Smith, D. F. (1953). "The Microwave Spectrum and Structure of Chlorine Trifluoride". The Journal of Chemical Physics. 21 (4): 609–614. Bibcode:1953JChPh..21..609S
- ↑ http://webbook.nist.gov/cgi/cbook.cgi?ID=C7790912&Units=SI&Mask=800#Electronic-Spec