Module3

Cope rearrangement

Optimising the reactants and products

There are 6 possible conformers of 1,5-hexadiene each with its own energy and point groups. Some possible conformers were optimized and there potential energies calculated . Frequency calculations were also performed to ensure that minimum energy conformer has been computed and also to examine molecular vibrations of those molecules. First molecules were optimised at the HF/3-21G level of theory and then symmetrized to obtain the point group. Eventhough from previous knowledge we might assume that the antiperiplanar arrangement would be of lower energy in the case of 1,5-hexadiene this is not true , as the gauche conformations have lower energies.Based on this observation the lowest energy conformer was predicted to be gauche as well(gauche3). Next step was optimising one conformer(anti2) at a higher B3LYP/6-31G* level of theory. This resulted in the decrease in energy when compared to HF/3-21G level of theory(-231.69254 to -234.61171)The point group remained the same (Ci) and the geometry didn't alter much. C=C and terminal C-H bonds were optimized to be slightly longer(1.33 compared to 1.32 and 1.09 compared to 1.07) , but C-C were slightly shortened(1.33 from 1.32).

Conformer	Structure	Point Group	Energy/Hartrees	Relative Energy/kcal/mol
gauche2		C₂	-231.69167	0.62
gauche3		C₁	-231.69266	0.00
anti1		C₂	-231.69260	0.04
anti2		C_i	-231.69254(3-21G) -234.61171(6-31G)	0.08

To be able to compare calculated energy values with experimental values , frequency calculation needs to be performed(All the frequency calculations are made using a harmnonic approximation model that would slightly deviate from the experimental vibrations especially at low frequencies) .This is because the energy recorded in the table above corresponds to the energy value on the potential energy curve(e.g it does not account for temperature)After calculation was complete , it could be proven that the structure represented a minimum as all the frequencies were real and positive. As can be seen energy values have been corrected, sum of electronic and zero-point Energies corresponds to the energy at 0K and sum of electronic and thermal energies reflects the energy of the conformer at 298K.

 Sum of electronic and zero-point Energies=           -234.469204
 Sum of electronic and thermal Energies=              -234.461857
 Sum of electronic and thermal Enthalpies=            -234.460913
 Sum of electronic and thermal Free Energies=         -234.500777

Links

Optimisation(anti 1)(321G)

Media:1_5_hexadiene_anti.chk

Optimisation (anti 2)(321G)

Media:1_5_hexadiene_anti_2.chk

Optimisation (anti 2)(631G(d))

Media:1,5_hexadiene_anti(2)_631G_trial_2.log

Optimisation (gauche2)(321G)

Media:1_5_hexadiene_gauche.chk

Frequency

Media:1_5_hexadiene_anti_2_631G_frequency_trial_2.log

Optimisation (gauche3)(321G)

Media:1_5_HEXADIENE_GAUCHE_3.LOG

Optimising transition states

Cope rearrangement is known to proceed in a concerted manner via two transition states, boat and chair, with boat being slightly higher in energy.In this part two transition states were optimised by 3 different methods and then activation energies of the Cope rearrangement were calculated via transition states.

Chair

First a predicted structure has to be drawn , this was done by optimising an allyl fragment using HF/3-21G level of theory and then manually arranging two allyl fragments into predicted chair conformation, making sure the distance between the carbon backbones is very close to 2.2 A and also overall allyl parts are directly above each other in the right position.

Method 1

Optimsation(to a TS Berny) and frequency calculation(force constant calculated once) was carried out(i.e the force constant matrix was computed) and that resulted in the structure with one imaginary vibration(indicative of the transition state) at 818 cm^-1 which corresponds to the Cope rearrangement motion.This method was possible because we had a close idea of how the transition state should look like.

Vibration

Media:Optimisation_chair_1_b.log

Method 2

In case our predicted structure of the chair transition state is far from the exact structure the calculation may not work , therefore to avoid this problem another way of optimising transition state is to freeze the reaction coordinate and optimise the rest of the molecule to a minimum. The reaction coordinate would lie between the end carbons of the two allyl fragments which form/break bond during the reaction. In the second step reaction coordinate was unfrozen and the full structure was optimised to a TS state, however this time the force time wasn't calculated.The first optimisation didn't converge , therefore the optimisation step was repeated.

If we compare the TS structures optimised by both methods It can be seen that the bond lengths and the distance between the allyl fragments is very similar this could be due to the fact that the guessed structure of the transition state was close to the exact structure and therefore the first method gave the correct optimisation. (1.39 A(C-C) bond length , 2.02 A (distance between allyl fragments)

Links Optimised TS structure Media:OPTIMISATION_CHAIR_1_D_TWICE.LOG

Boat

Third method of TS optimisation is used to find boat transition state.This method relies on interpolating between given reactant and product. For this part the previously optimised structure of anti2 1,5-hexadiene was put alongside the product structure with atoms numbered accordingly.The molecules are optimised using TS (QST2) , however the optimsation failed as it interpolates linearly without rotating around the bonds. Therefore structure has to be preset in a geometry that atoms are going to adapt in the transition state. Optimisation was run sucessfully and one imaginary vibration was present(indicative of the transition state) at -840 cm^-1 which corresponds to the Cope rearrangement.

Failed optimisation

Vibration of the TS

Vibration

Links

Failed Optimisation Media:OPTIMISATION_BOAT_QST2_FAIL.LOG

Sucessful optimisation+vibration Media:OPTIMISATION_BOAT_QST2_MODIFIED.LOG

Activation energies

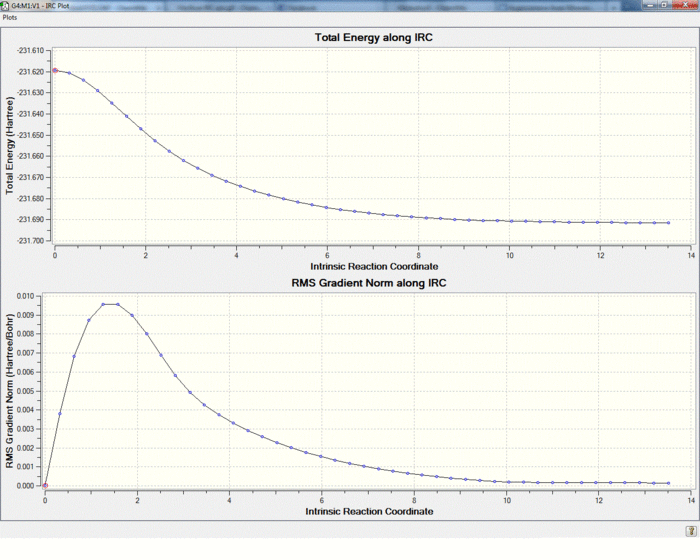
To find out the local minima of the optimised transition state IRC(Intrinsic reaction coordinate method) was used. It works by the principle of following the path with the steepest gradient along the potential energy curve. To reach a complete geometry minimum the force constant was computed at every step of calculation.Also for the boat confirmation the number of points along IRC was increased.As can be seen the final conformations have been reached because the gradient have fallen to 0, and the energy has reached a constant value. There is an interesting observation in the boat IRC analysis . As can be seen after the gradient has dropped to 0 , it started to increase again followed by the decrease to 0. This can be explained by the fact that the first minimum corresponds to the bond formation , then the energy is increased as the molecule is changing its conformation(to gauche3)

Chair transition state

(gauche2)

Boat transition state

(gauche3)

The boat transition state which is at higher energy than the chair transition state leads to the lowest energy conformation(gauche3). Chair transition state leads to the second lowest conformation (gauche2). Now the structures of products and transition states were optimised at a higher theory level(6-31g*). Now we can compare activation energies to the experimental values. Also it is shown that calculation at a higher level of theory was necessary as the energies differ significantly.

Links

IRC chair Media:OPTIMISATION_CHAIR_1_D_TWICE_IRC.LOG

IRC boat Media:OPTIMISATION_BOAT_QST2_MODIFIED_IRC.LOG

Boat TS 631G DOI:10042/to-22150

Chair TS 631G DOI:10042/to-22129

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466704	-231.461344	-234.556983	-234.414928	-234.409006
Boat TS	-231.602802	-231.450934	-231.445305	-234.543093	-234.402343	-234.396007
*Reactant (anti2)*	-231.692535	-231.539540	-231.532566	-234.611710	-234.469204	-234.461857

Activation energy(chair)= 34.8 kcal/mol(6-31G* , 0 K); 33.2 kcal/mol(6-31G* , 298K); lit. 33.5 kcal/mol <sup>1</sup>(using (6,6)-
CASPT2/6-31G*)
Activation energy(boat)= 42.0 kcal/mol(6-31G* , 0 K); 41.3 kcal/mol(6-31G* , 298K); lit. 44.7  kcal/mol <sup>1</sup>(6,6)-
CASPT2/6-31G*)
Difference between two activation energies(1t 0K) = 7.2 kcal/mol(lit. 11.0kcal/ mol)<sup>1</sup>

As can be seen our calculated values are in close agreement to the literature values , however depending on the basis set the calculations would give different values, therefore it is better to compare the difference between the activation energies of boat and chair, which was calculated to be 7.2 kcal/mol, which is not that close to the literature difference value.

Reference

1.Mahmood M. Khaledy, Mohammad Y. S. Kalani, Kelli S. Khuong, and K. N. Houk J. Org. Chem, Vol. 68, No. 2, 2003

Diels Alder cycloaddition

Using the tools investigated in the previous section transition state of the Diels Alder cycloaddition is going to be predicted

Butadiene

First butadiene is going to be optimised and MO prediction carried out. The optimisation was eventually carried out to a 6-31G* level of theory. Then the ethylene has been optimised in a similar manner to predict which MOs are going to interact to form a Diels Alder product.

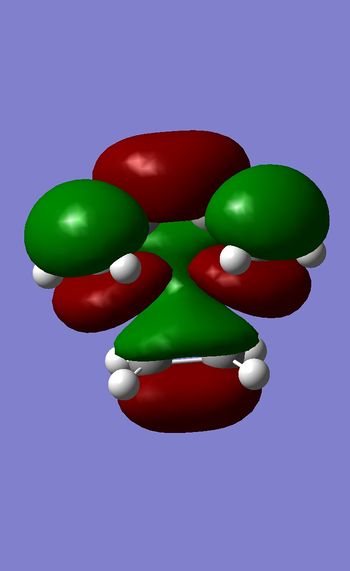
Ethene LUMO

LUMO is symmetric with respect to the plane of symmetry(perpendicular to the C=C) HOMO is antisymmetric with respect to the symmetry plane. The LUMO of ethene is also antisymmetric with respect to the plane , and therefore an efficient overlap(same symmetry) can be formed betweeb HOMO(butadiene) and LUMO(ethene).The HOMO donates electron density to the LUMO.

Links

Butadiene optimisation(6-31G(d,p)  Media:BUTADIENE_631_OPTIMISATION.LOG
MO analysis Media:Butadiene_631_optimisation_MO.chk

Transition state

In order to get an optimised Diels Alder transition state,method 1 from the previous section was attempted , but the structure of the transition state wasn't predicted close enough to the exact transition state, therefore when optimised it gave the wrong geometry. The second method then was used , where the distance between carbons(where the new bond should be formed) was fixed to 2.2 A , because this is generally the distance for C-C bond formation.After the first calculation , the reaction coordinate was unfrozen and the molecule was optimised again.

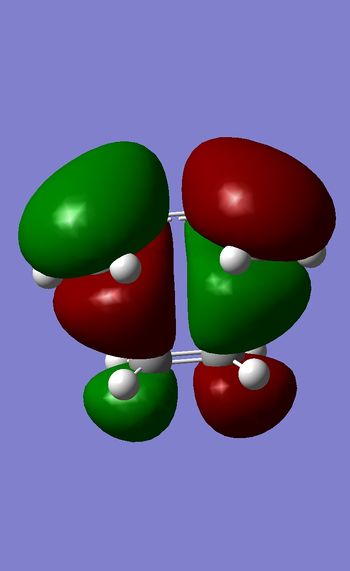
LUMO

HOMO

Both LUMO is symmetric with respect to the plane of symmetry.However HOMO is antysymmetric with respect to the plane.This is due to the fact mentioned above that to form a Diels-Alder product HOMO of diene and LUMO of dienophile will combine , and because they are both antisymmetric that will result in the antisymmetric orbital in the TS. Therefore this reaction is formally allowed as we are combining orbitals of the same symmetry. Bond lengths of newly formed C-C bonds=2.27 A

Reference bondlengths²

Typical sp³ bond distance=1.53 A

Typical sp² bond distance=1.34 A

van der Waals radius= 1.7 A

Length of newly C-C formed bonds= 2.1 A

From comparing the distance of a partly formed new C-C bond and other reference bond lengths It can be seen that two carbons are already closer to each other than their van der Waaks radii , however the distance between them is still much longer than reported C-C and C=C bond. Therefore it can be suggested that it is an early transition state (i.e similar in structure more to reactants than to products)

Reference 2.W.M.Haynes,CRC book of chemistry and physics(92nd edition)

Vibration corresponding to a transition state.

Vibration

Formation of two bonds is synchronous and the frequency of the vibration is at -818 cm^-1 (3-21G basis set). This would suggest a concerted mechanism. The first positive real vibrations comes at 165cm^-1 The motion of the real vibration is perpendicular to the transition state motion , and consists of the partial rotation of carbon backbone clockwise /anticlockwise and bends of C-H bonds.Also the first real vibration would require less energy than the vibration corresponding to the bond formation , as it would require bond stretching , compared to bond bending and translation.

Links

TS Optimisation(AM1 semi-imerical)frozen coordinate method(frequency) Media:TRIAL_D_SEMIIMPERICAL.LOG

Study of the regioselectivity of the Diels Alder Reaction

For more efficient reaction an electron rich diene and electron deficient dienophile should be used. HOMO of electron rich molecule is raised in energy and LUMO of electron-deficient molecule is lowered in energy , which provides a good overlap. Looking at this reaction it can be seen that substituting hetero atoms into dienophle causes additional interaction between two molecules and that influences the regioselectivity and stereoselectivity of the reaction. Same method for TS optimisation was used , because first method proved to be inefficient , and QST2 method would be unreliable , as all the reactants(two in this reaction) and products would have to be precisely aligned for the formation of the correct TS. Therefore the reaction coordinate was frozen again and TS optimisation was carried out.The molecules then were optimised to 6-31G theory level , and their imaginary vibrations were recorded and MO computed.

Comparision between exo and endo transition states

	Energy	Newly formed C-C bond length	C-C through space distance between -(C=O)-O-(C=O)- fragment and opposite C-C/C=C fragment	Vibration frequency
Exo	-612.67931	2.29 A	3.03 A	-448 cm^-1
Endo	-612.68340	2.27 A	2.99 A	-447 cm^-1

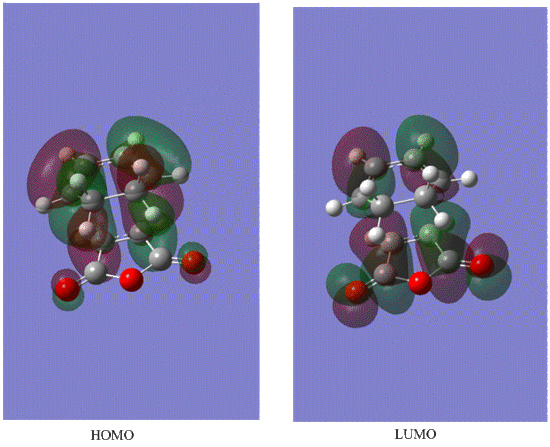
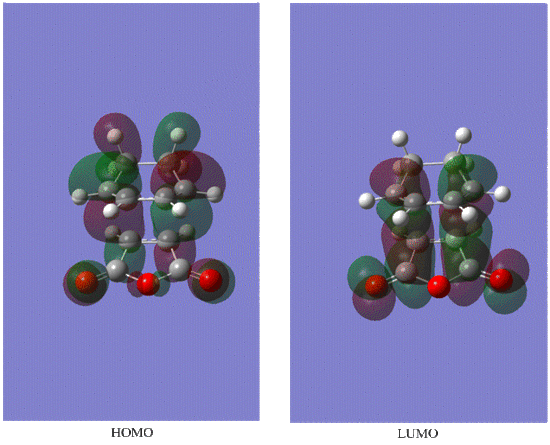
Diels-Alder is a kinetically controlled reaction , because the predominate product of this reaction is endo , which is less thermodymnamically stable as it is more sterically congested as indicated by shorter distances of newly formed C-C bonds and between two original reagent fragments of the molecule(i.e newly formed C-C bond and C-C through space distance between -(C=O)-O-(C=O)- fragment and opposite C-C/C=C fragment) compared to the exo conformer.However this through space interaction stabilises the endo TS and that's why it has lower energy than exo TS. Difference in structure is also due to the secondary orbital interactionas (can be seen from the HOMO MO diagram below) between the pi systems of C=C and the opposite -(C=O)-O-(C=O)- , which has a bonding character due to partially broken/formed C=C pi bonding . Secondary orbital interaction implies that not only the HOMO and LUMO contribute to the bonding in TS but also the MOs which are close in energy(e.g HOMO-1 or LUMO+1) as to examine the precise perturbations of each molecule the overlap integrals have to be calculated. In the exo case there is less interaction as the fragments are too far away from each other and the carbons opposite the carbonyl groups are sp₃ hybridised and therefore dont form a delocalised pi system as the sp₂ hybridised carbons do. Also due to secondary orbital interaction the endo transition state is lower in energy than exo transition state. Also it can be suggested that the longer space distance in exo is also due to a sterics clash between the oxygen groups of maleic anhydryte and the CH₂-CH₂ (compared to CH=CH in endo). The bond lengths within the each molecule are quite similar and are indictaive of the type of bond which is formed in the product. If we refer to the literature C-C bond lengths mentioned above it can be seen that the C=C bonds which are forming(1.39A) isare aproaching 1.34A bond length of a typical C=C. Double bonds which are breaking are slightly longer(1.4 A) , and are still far off from a C-C literature bond length , this can be due to the fact that the two molecule through space distance is still only within van der Waals radii from each other(not within C-C bond distance) and therefore supports an argument of this being an early transition state. The C-C bond which is going to be bridging is slightly longer than a typical C-C bond , this is due to the strain it would experience.

Endo

Exo

Imaginary vibrations of the TS state show the formation of the C-C bond. The frequency for both TS is approximately the same.However it seems to vary depending on the theory level of basis set, 6-31G optimisation was taking as a reference , because the structure shown represented the TS the most( partially formed/broken C=C bonds instead of C=C which were originally present in the reactants)

Some effects have been neglected in calculations of Diels Alder transition states , as the calculation was performed on a single dienophile and diene it wouldn't account for interactions which those molecules experience in solution, as reactants or as transition state. This can be linked to the electronic dipoles of the transition states and the relative degree of solvation, the higher the dipole the more molecule is going to be solvated . Also some approximations to carry out the calculation(harmonic oscillator model) can also influence the data which was obtained.

EXO

Vibration

Endo

Vibration

Links

Exo TS optimisation using frozen coordinate method (3-21G)
Media:GUESS_TS_TRIAL_1_D_TWICE.LOG
MO analysis(6-31G)
DOI:10042/to-22142 
631G Optimisation
DOI:10042/to-22143 
Frequency(6-31G)
DOI:10042/to-22144

Endo TS optimisation using frozen coordinate method(3-21G)
Media:GUESS_TS_TRIAL_2_D.LOG
TS Optimisation(6-31G)plus frequency calculation
DOI:10042/to-22145 
MO analysis(6-31G)
DOI:10042/to-22146