Rep:Mod:XYZ123
Introduction
The transition state of a reaction is the configuration with the highest potential energy along the reaction coordinate. A transition state cannot be observed due to its instability[1]. However using the Hammond-Leffler Postulate it can determined whether the structure is a Late Transition state - more closely resembles the products - or an Early Transition State - more closely resembles the reactants. Using computational chemistry the physical properties of transition states can be found, which the Hammond-Leffler Postulate does not provide[2]. In this experiment the program Gaussview was used to compute reactions and observe their transition states. Two different methods were used to do this and then compared with each other using the physical data obtained. The first method involved predicting a transition structure using the Hammond-Leffler Postulate, optimizing this to a minimum for a transition state and then calculating the vibrational energies to confirm the structure. The second method was called QST2 and involved drawing the reactants and products into Gaussview, and optimizing them together for a transition state. Both methods used two different levels of theory, the first being HF/3-21G, a more basic but less accurate level, and the second being B3LYP/6-31G, a more complex and accurate level.
Nf710 (talk) 17:48, 17 November 2015 (UTC) Some understanding of the different computational methods of DFT and HF would have been good here.
The Cope Rearrangement Tutorial
Background:
The Cope Rearrangement is a [3,3] sigmatropic rearrangement and fall under the category of pericyclic reactions. This reaction is closely related to the Claisen Rearrangement, with a C=C double bond in the place of the C=O double bond. For a pericyclic reaction to thermally occur it has to obey the Woodward-Hoffman rules[3]:
- The total number of (4q + 2)s + (4r)a must be odd.
- A component is a unit participating in the reaction and the number of electrons it uses in the reaction is what defines it.
- A suprafacial "s" component forms bonds on the same face at each end and an antarafacial "a" component forms bonds on opposite faces at each end.

Nf710 (talk) 17:50, 17 November 2015 (UTC) Nice use of the Woodward Hoffman rules
Optimizing the Reactants and Products:
Optimizing anti 1,5-hexadiene
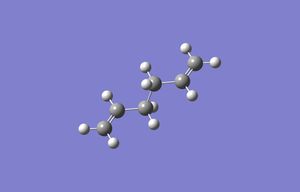

Molecule of 1,5-hexadiene drawn in Gaussview with an anti linkage - the dihedral angle is 180° - and the clean function used to set the geometry of the compound. The compound was then optimized at the HF/3-21G level to find the exact positions of the nuclei that give the lowest energy. The log file for the compound is given here. Energy obtained: -231.69253528 a.u. and symmetry point group obtained: Ci. This compound corresponds to the Anti2 compound in Appendix 1[1] , it has the correct symmetry and energy.
Optimizing gauche 1,5-hexadiene
Molecule of 1,5-hexadiene drawn in Gaussview with a gauche linkage and the clean function used to set the geometry of the compound. This compound was also then optimized at the HF/3-21G level. The log file for this compound is given here. Energy obtained: -231.69266120 a.u. and symmetry point group obtained: C1. This compound was of a more negative energy and a lower symmetry than the anti linkage compound.This compound corresponds to the Gauche3 compound in Appendix 1[2] , it has the correct symmetry and energy. This conformer is the lowest energy form of the transition due to there being less steric hindrance between the groups.
Higher level optimization of Anti2

Compound Anti2 was then optimized at the B3LYP/6-31G* level which determines the approximation types that are made when the Schrodinger Equation is used at a medium level of accuracy[4]. There is a big change in energy from the HF/3-21G optimized Anti2 structure, energy now is -234.61171149 a.u.. The geometry has not changed very much at all, visually the compound looks the same and the symmetry point group is still Ci. To compare the two anti structures, the numbering system below was used:
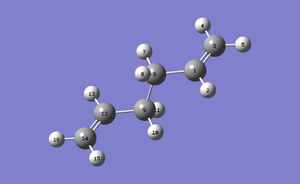
| Bond Lengths (Å) | ||
|---|---|---|
| Atoms | B3LYP | HF |
| C1-C3 | 1.33350 | 1.31613 |
| C1-C6 | 1.50419 | 1.50891 |
| C6-C9 | 1.54817 | 1.55275 |
Nf710 (talk) 17:58, 17 November 2015 (UTC) Your explanation of why the gauche is teh lowest energy is clearly wrong. the anti would have the lowest steric hinderance. the reason is due to the second order orbital interaction between the two pi systems. you could have seen this your self if you had look at the orbitals in the .chk file.
Nf710 (talk) 17:58, 17 November 2015 (UTC) It is is meaningless to compare a DFT calculation to a HF one. The Hamiltonians have different terms. you also did not compare the bind angles.
Frequency Calculation of Optimized Anti2
On the optimized Anti2 compound a frequency calculation was ran at the B3LYP/6-31G* level, which gives the IR and Raman modes of the molecule and calculates the second derivative of the potential energy surface[4]. All frequencies obtained were positive values and so there were no imaginary frequencies. The frequency log file can be found here.
Optimizing the "chair" and "boat" transition structures:
Building chair transition state
To begin, the chair transition structure was made. An allyl fragment was drawn in Gaussview and optimized at the HF/3-21G level. The log file for this is given here. This optimized structure was then pasted twice into a new molecule window to start creating the transition structure. One of the fragments was turned upside down and moved so above the other fragment, as seen in this picture. The fragments was then symmetrized to ensure both terminal ends of each allyl fragment were the same distance from the corresponding terminal ends of the other fragment. This distance was 2.04584 Å. Two different optimizations were then performed on the fragments.
HF/3-21G optimization of chair transition state
The structure created was pasted into a new molecule window and a HF/3-21G optimization for a transition state was performed on it. The force constants were calculated once and opt=noeigen was entered into the additional keywords box to stop the system crashing if more than one imaginary vibration arises. The log file for this is given here. An imaginary frequency was supposed to be obtained at 818 cm-1 and one was observed at 817.73 cm-1. This vibration is correct due to the fact that is is occurring where the sigma bonds will be formed and broken.
Chair transition state vibration |
Frozen coordinate optimization of chair transition state
Secondly the structure was optimized using the frozen coordinate mode at the HF/3-21G level. The structure created was once again pasted into a new molecule window. Using the redundant coordinate editor the distance between the terminal ends of each allyl fragment were frozen. The structure was then optimized to a minimum with opt=modredundant in the additional keywords box to ensure that the distances stay frozen whist the structure is optimized. the log file for this is given here.
The distances between the terminal ends then needed to be optimized. Using the redundant coordinate editor at the HF/3-21G level the distances are unfrozen and the structure is optimized for a transition state using the HF/3-21G optimization. This was then compared to the unfrozen optimization method.
| Method | Bond breaking length (Å) | Bond forming length (Å) |
|---|---|---|
| HF/3-21G | 1.38923 | 2.02057 |
| Frozen | 1.38929 | 2.02075 |
Both the bond breaking and bond forming lengths are very similar between the two methods of optimization.
QST2 optimization of Boat transition state
The boat transition structure was then made. The optimized Anti2 molecule made in the first part of the tutorial was pasted twice into a new molecule window but as two separate molecules, these were then rotated so they were the mirror image of each other. Using atom list, the atoms were numbered to tell Gaussview which atoms reacted together and then a QST2 calculation at the HF/3-21G level was ran for a transition state. This calculation failed, the reactant and product were not bent enough to provide the boat transition state.

To account for this the C2-C3-C4-C5 dihedral angle was changed to 0° and the C2-C3-C4 and C3-C4-C5 angles changed to 100°.
The calculation was ran again and this time the reactant and product converged into the boat transition state. The imaginary frequency at -839.49 cm-1 and the stationary point is at a maximum and so this is the correct boat transition structure for the Cope Rearrangement. The log file for this can be found here.
Boat transition state vibration |
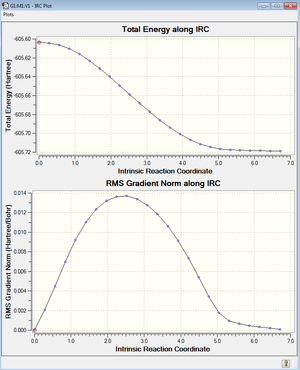
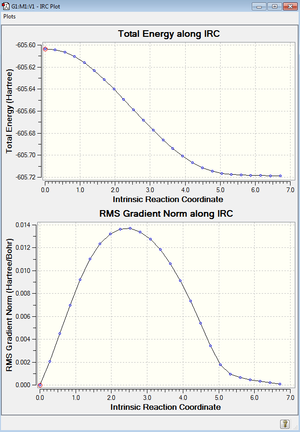
Intrinsic Reaction Coordinate of Boat Transition State
Next an Intrinsic Reaction Coordinate (IRC) at the HF/3-21G level was ran on the optimized chair transition structure from part b). It was chosen to compute the reaction coordinate only in the forward direction due to the reaction being symmetrical, as the reactant and product are the same. The log file of this is given here. The IRC gives a total energy plot, and on this it can be seen that the transition state changes to a minimum energy. A root mean square plot is also given and this shows the derivative of the total energy plot and when the product is produced (when the derivative equals zero).


Higher level of optimization of Transition States
The transition states were then optimized at a higher level of theory to calculate the activation energies for them both. Using the HF/3-21G level optimized structures, the transitions structures were re-optimized at the B3LYP/6-31G* level. The log file for the boat transition state is given here and the log file for the chair transition state is given here. The boat transition state has an imaginary frequency at -530.36 cm-1 whilst the chair transition state has one at -565.64 cm-1. The electronic energy of the boat transition state is -234.54309307 a.u. whilst the energy of the chair transition state is -234.55698263 a.u. This shows that the two transition stats are very close in energy but that the chair structure is slightly more stable.

Boat transition state vibration |
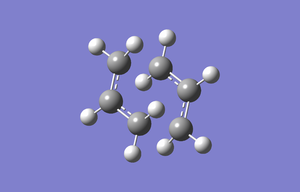
Chair transition state vibration |
Nf710 (talk) 18:13, 17 November 2015 (UTC) You havent compared the geometries
Thermodynamic Data
| B3LYP/6-31G* (All data in a.u.) | HF/3-21G(All data in a.u.) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | |
| Chair TS | -234.55698263 | -234.414929 | -234.409008 | -231.61932236 | -231.466698 | -231.461339 |
| Boat TS | -234.54309307 | -234.402342 | -234.396008 | -231.60280231 | -231.450928 | -231.445299 |
| Anti2 | -234.61171149 | -234.469215 | -234.461866 | -231.69253528 | -231.539539 | -231.532565 |
To then calculate the activation energy for the two transition states, the difference between the Sum of electronic and zero-point energies for the transition state and the Sum of electronic and zero-point energies for the Anti2 reactant was found. This value was then multiplied by 627.509 to get the units in kcal/mol.
| B3LYP/6-31G* (kcal/mol) | HF/3-21G | Expt. (kcal/mol) | |||
|---|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | 0 K | |
| ΔE (Chair) | 34.06 | 33.17 | 45.71 | 44.69 | 33.5 ± 0.5 |
| ΔE (Boat) | 41.96 | 41.33 | 55.60 | 54.76 | 44.7 ± 2.0 |
From this it can be seen that the chair transition state is closer in energy to the Anti2 reactant than the boat transition state is. Therefore the chair transition state will be formed quicker and will lead to the kinetic product. It can also be seen that by using a higher level of theory the computational value is closer to the expected value and therefore more accurate.
Nf710 (talk) 18:23, 17 November 2015 (UTC) You haven't compared the geometries and there fore you haven't come to the conclusion that lowest basis sets are good at getting the geom correct but bad at getting the energies.
Nf710 (talk) 18:23, 17 November 2015 (UTC) In general this is a fairly standard first section. You have attempted most things that have been asked of you and you have referenced literature. However you haven't shown much understanding of what is going in with the methods. such as What is the difference between DFT and HF and how is the frequency calculated and why is it imaginary
The Diels Alder Cycloaddition
(The calculations in this section should have been performed with at least AM1 Tam10 (talk) 11:43, 9 November 2015 (UTC))
Background:
A Diels Alder reaction is a [4+2] cycloaddition between a diene and an dienophile. During a Diels Alder reaction overall two pi bonds are broken and two sigma bonds are made, this make the reaction thermodynamically favoured as sigma bonds are more stable than pi bonds. The reaction schemes experimented on during this computational lab are given below
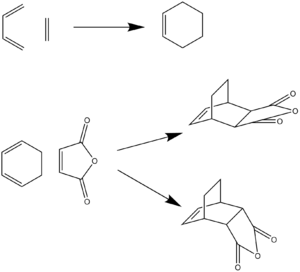
Ethylene + Cis-butadiene:
Cis-butadiene Optimization
Molecule of cis-butadiene was drawn in Gaussview and then optimized at the HF/3-21G level. The log file for this can be found here. The HOMO and LUMO were plotted and it was determined that the LUMO is symmetric with respect to the plane and the HOMO is antisymmetric with respect to the plane.


Computation of the Transition State Geometry
The transition state is an envelope shape to maximize the overlap of the pi orbitals of ethylene with the pi system of butadiene. This was drawn in Gaussview with dotted lines where the bonds would be formed between ethylene and butadiene, at a length of 2Å. This structure was then optimized to a transition state at the HF/3-21G level and after optimization the length of the dotted lines had increased to 2.20935Å. The log file for this is given here. There is an imaginary frequency at -818.65 cm-1 with the vibration occurring where the bonds will form.
(There is no mention of whether the bonding is synchronous or asynchronous Tam10 (talk) 11:43, 9 November 2015 (UTC))
Transition state vibration |


Both the LUMO and HOMO are symmetric with respect to the plane.
(Which MOs of ethene and butadiene contribute to the HOMO and LUMO of the TS? And why is this reaction allowed? Tam10 (talk) 11:43, 9 November 2015 (UTC))
The picture below shows the numbering system used for the bond lengths in the table below.

| Atoms | Bond Lengths (Å) |
|---|---|
| C1-C2 | 1.39446 |
| C2-C14 | 1.37003 |
| C14-C8 | 2.20935 |
| C8-C5 | 1.37623 |
| C5-C11 | 2.20992 |
| C11-C1 | 1.37007 |
From literature an sp3 C-C bond length is 1.525-1.530 Å and an sp2 C=C bond length is 1.335 ± 0.01 Å[5]. The van der Waals radii of the carbon atom is 1.7 Å. The partly formed sigma C-C bonds (C14-C8 and C5-C11) are a lot longer than the van der Waals radii of a carbon atom, therefore they are currently only bonding interactions.
Cyclohexa-1,3-diene + maleic anhydride:
Cyclohexadiene optimization
Structure of cyclohexadiene was drawn in Gaussview and optimized at the HF/3-21G level. The log file for this is given here.
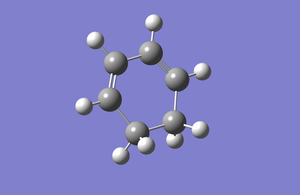
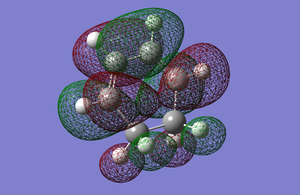
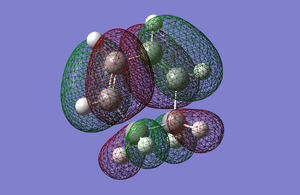
HOMO is symmetric with respect to the plane and the LUMO is antisymmetric with respect to the plane.
Maleic Anhydride optimization
Structure of maleic anhydride was drawn in Gaussview and optimized at the HF/3-21G level. The log file for this can be found here.


HOMO is symmetric with respect to the plane and LUMO is antisymmetric with respect to the plane.
Exo transition state optimization
Optimized reactants pasted into same new molecule window and arranged as the exo product. This was then optimized at the HF/3-21G level, and pasted twice into a new molecule window on separate pages. The log file for the HF/3-21G optimization can be found here. For the reactant page, the bonds formed during the reactant were taken out and the bonds broken were put in. The bond angles were also adjusted so the two reactants were more planar than the product.
A QST2 optimization for a transition state was then run and the transition state found. The log file for this can be found here. Using this optimized structure, a further optimization at the B3LYP/6-31G* level was ran. The log file for this can be found here.
Exo Transition state vibration |
An IRC of the transition state was also ran. The log file for this can be found here.
The HOMO and LUMO of the exo transition state can be seen below and are a combination of the Maleic anhydride and Cyclohexadiene orbitals.

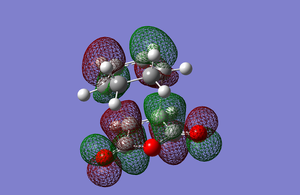
Both orbitals are antisymmetric with respect to the plane. It can be seen in the HOMO that the orbitals from the reactants match up where the new sigma bonds are forming and that there are nodes in between the carbon atoms that are being bonded together. It can also be seen that the HOMO is made up of the HOMO from cyclohexadiene and the LUMO from maleic anhydride. The energy of this transition was -612.67931089 a.u.
Endo transition state optimization
Optimized reactants pasted into same new molecule window and arranged as the endo product. This was then optimized at the HF/3-21G level, and pasted twice into a new molecule window on separate pages. The log file for the HF/3-21G optimization can be found here. For the reactant page, the bonds formed during the reactant were taken out and the bonds broken were put in. The bond angles were also adjusted so the two reactants were more planar than the product.

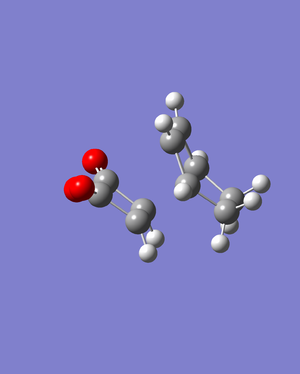
A QST2 optimization for a transition state was then run and the transition state found. The log file for this can be found here. Using this optimized structure, a further optimization at the B3LYP/6-31G* level was ran. The log file for this can be found here.
Endo Transition state vibration |
An IRC of the transition state was also ran. The log file for this can be found here.
The HOMO and LUMO of the exo transition state can be seen below and are a combination of the Maleic anhydride and Cyclohexadiene orbitals.
(Typo here. This would be easier to detect if your presentation was more space efficient. Perhaps reorienting your MOs below will allow you to explain the secondary overlap effect more easily Tam10 (talk) 11:43, 9 November 2015 (UTC))
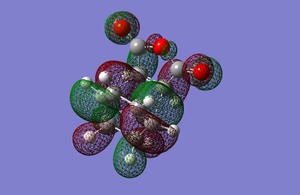

Both orbitals are antisymmetric with respect to the plane. As with the exo transition state it can be seen in the HOMO picture that the orbitals match along where the carbon sigma bonds are forming between the two reactants and that there are no nodes between the carbon atoms that are being bonded together. It can also be seen that the HOMO of the transition state is made up of the HOMO of maleic anhydride and the LUMO of cyclohexadiene. The energy of this transition state was -612.68339656 a.u.
Comparison of Transition States
For comparison of bond lengths, the atoms in the endo structure were numbered as in the picture below.
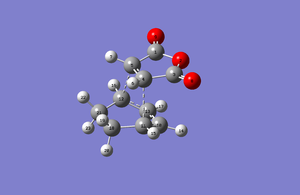
| Atoms | Bond Lengths (Å) |
|---|---|
| C1-C5 | 1.47949 |
| C5-C4 | 1.39401 |
| C4-C3 | 1.47949 |
| C5-C12 | 2.26844 |
| C4-C11 | 2.26847 |
| C12-C13 | 1.39127 |
| C13-C10 | 1.40308 |
| C10-C11 | 1.39127 |
| C11-C18 | 1.51507 |
| C18-C21 | 1.55822 |
| C12-C21 | 1.51507 |
The atoms in the exo structure were numbered as in the picture below.

| Atoms | Bond Lengths (Å) |
|---|---|
| C1-C5 | 1.47942 |
| C5-C4 | 1.39793 |
| C4-C3 | 1.47942 |
| C5-C11 | 2.29062 |
| C4-C12 | 2.29063 |
| C12-C13 | 1.39142 |
| C13-C10 | 1.40345 |
| C10-C11 | 1.39142 |
| C11-C18 | 1.51453 |
| C18-C21 | 1.55837 |
| C12-C21 | 1.51453 |
Below is a sketch of the exo and endo transition states with all the bond forming/breaking distances.

The bond length where the sigma bond is being formed is slghtly longer in the exo transition state than in the endo transition state. This shows that there is more steric repulsion between the reactants in the exo structure.
| B3LYP/6-31G* (All data in a.u.) | HF/3-21G(All data in a.u.) | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | |
| Exo TS | -612.67931089 | -612.498013 | -612.487663 | -605.60359125 | -605.408139 | -605.398679 |
| Endo TS | -612.68339656 | -612.502143 | -612.491790 | -605.61036819 | -605.414907 | -605.405481 |
| Cyclohexadiene | -233.41587942 | -233.293224 | -233.288629 | -230.53967094 | -230.407712 | -230.403444 |
| Maleic Anhydride | -379.28953477 | -379.233648 | -379.228467 | -375.10351335 | -375.042901 | -375.038067 |
| B3LYP/6-31G* (kcal/mol) | HF/3-21G | |||
|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | |
| ΔE (Exo) | 18.11 | 19.74 | 28.48 | 28.72 |
| ΔE (Endo) | 15.02 | 16.97 | 23.94 | 24.16 |
Here it can be seen that the endo transition state is closer in energy to the reactants and will therefore be produced quicker and will lead to the kinetic product.
Secondary orbital overlap occurs in a transition state in addition to the primary orbital overlap where the bonds are formed. The secondary orbital interaction does not lead to bond formation but contributes to lowering of the energy of the transition state. This occurs through the pi orbital overlap with the C=O on the dienophile and the C=C on the diene. In the endo transition state this occurs more than than in exo transition state, resulting in its lower energy.
Conclusion
In this computational lab two reactions were investigated: The Cope Rearrangement and the Diels Alder Reaction. Both were computed under two levels of theory with the program Gaussview, using different methods to obtain a transition structure for the reaction. The two level of theory used were HF/3-21G and B3LYP/6-31G*, and from this experiment it was found that the B3LYP/6-31G* level of theory produced more accurate results than the HF/3-21G level of theory, but took more time to compute the transition states. From this experiment it was found that for every reaction the transition state showed one imaginary frequency with the vibration occurring where the new sigma bonds would form.
To improve the experiment, for the cope rearrangement the oxyanionic-cope could be studied. During the transition state formation and decay for this reaction conjugation occurs between the oxyanion and developing new pi bond.It would be interesting to view the MOs for this. For the diels alder reaction an intramolecular reaction could be studied. This would be interesting to see what conformers are formed for the transition state and which is the lowers energy.
Reference
- ↑ Grayam TW Solomons and Craig B Fryhle. Organic Chemistry (8th ed.). John Wiley and Sons: 2004.
- ↑ Thomas A Manz and David S Sholl. A dimensionless reaction coordinate for quantifying the lateness of transition states. J. Comput. Chem: 2009. Available from doi:10.1002/jcc.21440 [Accessed 4th November 2015].
- ↑ Sue Gibson. Sigmatropic Rearrangements. [Lecture] Pericyclic Reactions. Imperial College London. 12th March 2015.
- ↑ 4.0 4.1 Tricia Hunt. Hunt Research Group. Available from http://www.huntresearchgroup.org.uk/teaching.html [Accessed on 30th October 2015].
- ↑ David R Lide. A survey of carbon-carbon bond lengths. Tetrahedron. 1961;17(3): 125-134. Available from http://www.sciencedirect.com/science/article/pii/S004040200199012X [Accessed on 5th November 2015.
