Rep:Mod:XJB1130

The Cope Rearrangement of 1,5-hexadiene

The Cope rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic rearrangement reaction (Figure 1). Its mechanism has been studied by a large number of experimental and computational researches, which is recently accepted that the reaction occurs via either a "chair" or a "boat" transition state structure in a concerted manner. The aim of this exercise is to locate the low-energy minimum and the transition structures on the potential energy surface by Gaussian calculation in order to study its mechanism. The reaction pathway and the activation energy can also be calculated by this calculation.

Optimizing the Reactants and Products

Different conformations of 1,5-hexadiene can be optimized using Gaussview. The optimized structure of four conformers involved in this discussion and their corresponding energies optimized at HF/3-21G level of theory are concluded in the following table (Table 1).

anti4

anti2

gauche

gauche3

XJB_anti4.mol

XJB_anti2.mol

XJB_gauche.mol

XJB_gauche3.mol

-231.69097Ha

-231.69254Ha

-231.68772Ha

-231.69266Ha

Table 1. Four conformers of 1,5-hexadiene

This exercise first involved optimizing a molecule of 1,5-hexadiene with "anti" linkage for the cetral four C atoms at the HF/3-21G level of theory. The final optimization structure had the total electronic energy of -231.69097Ha with a C₁ symmetry. By comparing the energy and point group to that in Appendix 1, this structure is confirmed to be anti4. The compositions of energies are also listed in Table 2 as i) the sum of electronic and zero-point energies (potential energy at 0K including the zero-point vibrational energy), ii) the sum of electronic and thermal energies (energy including translational, rotational and vibrational at 298.15K and 1 atm), iii) the sum of electronic and thermal enthalpies (containning an additional correction for RT), and iv) the sum of electronic and thermal free energies (including the entropic contribution to the free energy). For what we are considering, the first two terms are the most useful for further comparisons.


Types of Energies	Formula Description	Energy/Hartrees (HF/3-21G)
Sum of electronic and zero-point Energies	E = E_elec + ZPE	-231.53785
Sum of electronic and thermal Energies	E = E + E_vib + E_rot + E_trans	-231.53096
Sum of electronic and thermal Enthalpie	H = E + RT	-231.53002
Sum of electronic and thermal Free Energie	G = H - TS	-231.56891

Table 2. Frequency calculations of anti4 optimized at HF/3-21G (File:XJB anti4.log)

Next another 1,5-hexadiene molecule with "gauche" linkage for the central four atoms was drawn and optimized at the HF/3-21G level of theory as before. Energy for this conformation is expected to be higher than that for the anti4 conformation due to the closer position of two alkene ends thus the steric interaction. The final structure had the electronic energy of -231.68772Ha which was indeed higher than that of the anti4, indicating less favour towards this gauche structure. It had a C₂ symmetry and was confirmed to be the gauche conformation.


Types of Energies	Energy/Hartrees (HF/3-21G)
Sum of electronic and zero-point Energies	-231.53439
Sum of electronic and thermal Energies	-231.52770
Sum of electronic and thermal Enthalpie	-231.52676
Sum of electronic and thermal Free Energie	-231.56483

Table 3. Frequency calculations of gauche optimized at HF/3-21G (File:XJB gauche.log)

A lowest energy conformation gauche3 of the reactant molecule was drawn based on and confirmed by Appendix 1. The optimization gave a final structure with an energy of -231.69266Ha with a symmetry of C₁.


Types of Energies	Energy/Hartrees (HF/3-21G)
Sum of electronic and zero-point Energies	-231.53949
Sum of electronic and thermal Energies	-231.53265
Sum of electronic and thermal Enthalpie	-231.5317
Sum of electronic and thermal Free Energie	-231.57064

Table 4. Frequency calculations of gauche3 optimized at HF/3-21G (File:XJB gauche3.log)

The next step required us to draw the C_i symmetry anti2 conformation of 1,5-hexadiene and optimize it at the HF/3-21G level of theory. The optimized energy was calculated to be -231.69254Ha with point group of C_i, which was consistent with the one given in Appendix 1.


Types of Energies	Energy/Hartrees (HF/3-21G)
Sum of electronic and zero-point Energies	-231.53954
Sum of electronic and thermal Energies	-231.53257
Sum of electronic and thermal Enthalpie	-231.53162
Sum of electronic and thermal Free Energie	-231.57092

Table 5. Frequency calculations of anti2 optimized at HF/3-21G (File:XJB anti2.log)

The anti2 structure was then reoptimized at B3LYP/6-31G* which was a improvement over the HF/3-21G basis set. It adds polarization to atoms and improves the modeling of core electrons thus producing more accurate description of orbitals^[1]. The reoptimized anti2 structure had the total electronic energy of -234.61171Ha and the same symmetry C_i. The comparison of two structures optimized using different levels of theory is summarized in Table 6. We can see that they have exactly the same dihedral angle of the central four C atoms at 180.00^o and angles between three of them are very similar as 111.3^o and 112.7^o respectively. Thus the the geometry change using HF/3-21G or B3LYP/6-31G* is trivial.

Before re-optimization

After re-optimization

XJB_anti2.mol

XJB_anti2reoptimized

anti2 optimized at HF/3-21G

anti2 optimized at B3LYP/6-31G*

Table 6. Two optimization of anti2 at HF/3-21G and B3LYP/6-31G*(File:XJB anti2.log)

The frequency calculation was run as well and a list of energies is summarized in Table 7. A list of all the vibrational frequencies was also generated and no imaginary (negative) frequency was observed and these vibrations are visualized by simulating the infrared spectrum in Figure 2.


Types of Energies	*Energy/Hartrees (B3LYP/6-31G)**
Sum of electronic and zero-point Energies	-234.46920
Sum of electronic and thermal Energies	-234.46186
Sum of electronic and thermal Enthalpie	-234.46091
Sum of electronic and thermal Free Energie	-234.50078

Table 7. Frequency calculations of anti2 optimized at B3LYP/6-31G*

(File:XJB anti2 reoptimized.log)

Figure 2. The generated IR spectrum of optimized B3LYP/6-31G* structure

Optimizing the "Chair" and "Boat" Transition Structures

The study of the chair and boat transition states was carried out using three different approaches. The first one was called the Hessian which involved computing the force constant matrix; the second one was to freeze the reaction coordinate and then optimized the structure once the molecule was fully relaxed; the last one was to use QST2 method to specify the reactants and products then finding the transition structure.

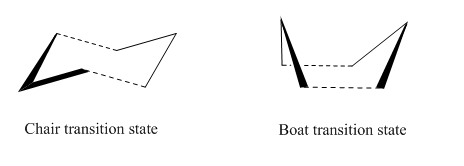
**Figure 3**. *The two transition states of Cope rearrangement*

The Chair Transition State

In order to set up a transition state optimization, first an allyl fragment (CH₂CHCH₂) was drawn and optimized at the HF/3-21G level of theory. Then this half of the transition structure was duplicated with rotation to make the approximate resembling of the chair transition state with terminal ends of the fragments 2.2 Å apart. The chair transition structure optimization was then done by the first two different approaches.

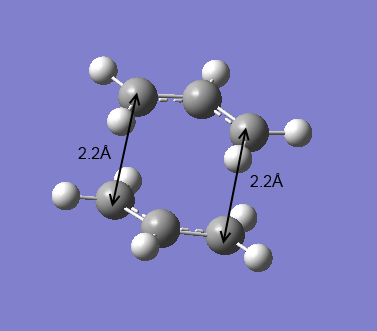
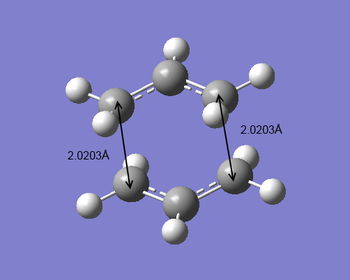
**Figure 4**. *The guessed chair transition structure of two allyl fragments*

For the first optimization approach, the force constants were computed (the Hessian) and the chair transition state was optimized to a TS (Berny) at the HF/3-21G level of theory. The frequency calculation was carried out at the same time and gave an imaginary frequency at -818 cm^-1. The electronic energy was calculated to be -231.61932Ha with C_2h symmetry point group. The distance between the terminal carbons was 2.0203 Å. An animation of this transition state vibrations was generated to confirm the corresponding Cope rearrangement.

The chair transition state was then reoptimized using the B3LYP/6-31G* level of theory and carried out frequency calculations as well. The electronic energy calculated this time was -234.55698Ha with an imaginary frequency at -566 cm^-1. We can see that with the geometries quite similar, the energies differ markedly calculated using two levels of theory. The summary and comparison of the calculations optimized at two levels of theory are summarized in Table 8.


Types of Energies	Energy/Hartrees (HF/3-21G)	*Energy/Hartrees (B3LYP/6-31G)**
Sum of electronic and zero-point Energies	-231.46670	-234.41493
Sum of electronic and thermal Energies	-231.46134	-234.40901
Sum of electronic and thermal Enthalpie	-231.46040	-234.40807
Sum of electronic and thermal Free Energie	-231.49521	-234.44381
Generated IR spectrum
	File:XJB chairts1.1.log	File:XJB chairts1.2.log

Table 8. Frequency calculations of the chair transition structure optimized at HF/3-21G and (B3LYP/6-31G*) by the first approach

The second approach is the frozen coordinate method using the Redundant Coord Editor to freeze the bond lengths of the terminal ends to 2.2 Å. First the calculation failed because of the recent update of GaussView. After editting the coordinate distance (B 5 1 2.2 F) and the frozen distance (B 5 1 F) the optimization went well this time. The structure was then optimized again using a normal guess Hessian modified including the two differentiating coordinates. This chair transition state was then reoptimized again using the B3LYP/6-31G* level of theory. The electronic energies were calculated to be the same as in the first approach and frequency calculations were summarized in Table 9.


Types of Energies	Energy/Hartrees (HF/3-21G)	*Energy/Hartrees (B3LYP/6-31G)**
Sum of electronic and zero-point Energies	-231.46671	-234.41490
Sum of electronic and thermal Energies	-231.46135	-234.40901
Sum of electronic and thermal Enthalpie	-231.46040	-234.40806
Sum of electronic and thermal Free Energie	-231.49521	-234.44381
Generated IR spectrum
	File:XJB chairts2.1.log	File:XJB chairts2.2.log

Table 9. Frequency calculations of the chair transition structure optimized at HF/3-21G and (B3LYP/6-31G*) by the second approach

As the same energy results given, the bond forming/breaking bond lengths in the chair transition structures in the above two different approaches were compared. The first approach gave the bond lengths of 2.0203 Å while the second approach gave 2.0207 Å. Considering the accuracy limit of bond length estimation in Gaussview, these two bond lengths can be seen as exactly the same. Two methods worked reasonably well because of the good assumption of transition structures. However for more complicated and larger molecule, the Hessian method may fail due to the difficulty to predict the transition geometry (different surface curvature). Thus better way to generate such transition structures is to freeze reaction coordinate.

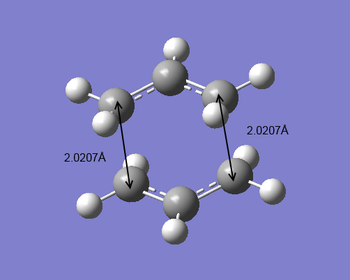The Boat Transition State

The boat transition structure was then optimized using the QST2 method. The same numbering for the reactant and product molecules was important in order to specify for this reaction. The renumbering of the molecules is shown as in Figure 8, but the following optimization failed and gave a twisted structure. The reactant and product geometries were then modified further by changing the central C-C-C-C dihedral angle to 0^o and the inside two C-C-C (i.e. C2-C3-C4 and C3-C4-C5) angles to 100^o. The job was run successfully and frequency calculations were done with the boat transition state generated. Only one imaginary frequency was detected at -840 cm^-1. The electronic energy was -231.60280Ha with C_2v symmetry. The distances between the terminal carbons of the allyl fragments were examined to be both 2.140 Å which were comparably longer than that of the chair transition structure.

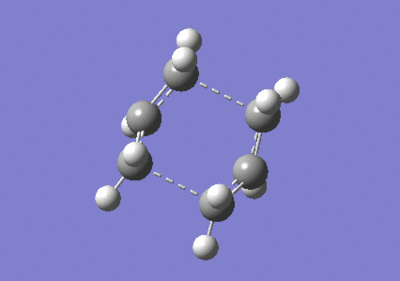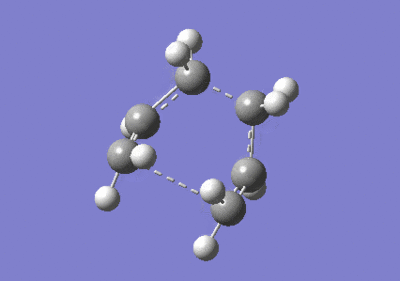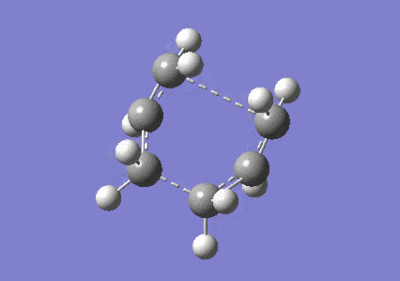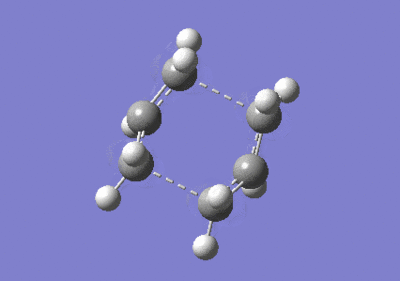
The structure was then reoptimized at the higher B3LYP/6-31G* theory of level and the electronic energy was calculated to be -234.54309Ha with very similar geometry. The frequency calculation generated an imaginary frequency at -530 cm^-1. The summary and comparison of two levels' calculations are carried out in the following table.


Types of Energies	Energy/Hartrees (HF/3-21G)	*Energy/Hartrees (B3LYP/6-31G)**
Sum of electronic and zero-point Energies	-231.45093	-234.40234
Sum of electronic and thermal Energies	-231.44530	-234.39601
Sum of electronic and thermal Enthalpie	-231.44436	-234.39506
Sum of electronic and thermal Free Energie	-231.47977	-234.43175
Generated IR spectrum
	File:XJB boat ts1.log	File:XJB boat ts2.log

Table 10. Frequency calculations of the boat transition structure optimized at HF/3-21G and (B3LYP/6-31G*) by QST2

Intrinsic Reaction Coordinate

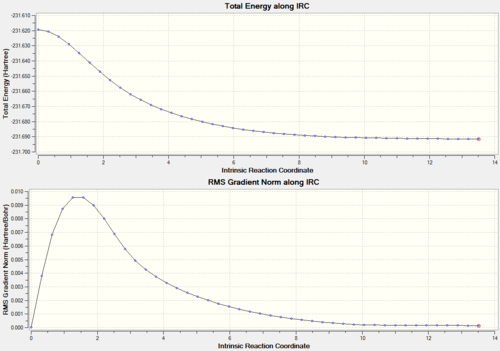
Next a useful method called Intrinct Reaction Coordinate (IRC) was applied to the Hessian optimized chair transition structure to follow the mininmum energy path (MEP) from a transition structure down to its local minimum on a potential energy surface. IRC can be used to verify that the transition state we found actually connects the reactants and products, or to identify any reaction intermediates, or to generate an animation of the reaction^[2]. The symmetrical reaction coordinate was computed only in the forward direction with force constant always calculated and the number of points along IRC 50. The last structure generated along IRC is given in Figure 11 with the energy calculated as -231.69158Ha and the dihedral angle of the central four C atoms and the internal angle between three C atoms measured as D = -67.188^o A = 111.78^o. This energy does not match to any of the conformations discussed in Appendix 1 thus a minimum geometry has not reached yet.

XJB_IRC.mol

Figure 11. The energy minimum structure along IRC (File:XJB IRC.log)

Figure 12. Total energy along IRC

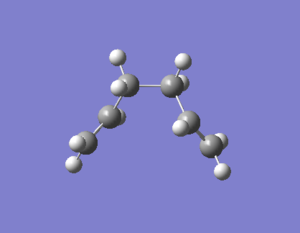
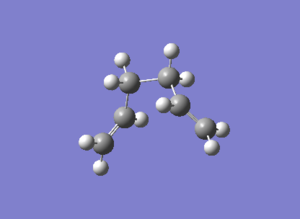
Three improving options can be used to reach the minimum energy. The first one is to run a normal Hessian optimization at the last point on IRC; the second one involves using a larger number of points (in this case 100 was used); the last one is to redo the IRC computation specifying to compute force constant at every step. Three methods were all used and the results were summarized in Table 11.


Improved IRC method 1	Improved IRC method 2	Improved IRC method 3
IRC1	IRC3	IRC3
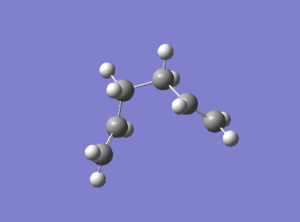D = -64.17^o A = 112.04^o	D = -66.83^o A = 111.82^o	D = -64.17^o A = 112.04^o
-231.69167Ha	-231.69150Ha	-231.69167Ha
File:XJB IRC1.log	File:XJB IRC2.log	File:XJB IRC3.log

Table 11. Comparison of three improvement methods of IRC computation upon the chair transition structure

The first method was very quick but maybe generated relatively low-accuracy result; the second approach involved the controlling of number of points which might result in ending up at the wrong direction and wrong structure; the third method was the most suitable option for this small system but it took longer time than the previous two. From Table 11 it is concluded that method 1 and 3 gave the same lowest energy which was consistent to the energy of the gauche2 conformation given in Appendix 1.

Activation Energies


	HF/3-21G at 0K	HF/3-21G at 298.15K	B3LYP/6-31G* at 0K	B3LYP/6-31G* at 298.15K	Expt. at 0K
ΔE (chair) in kcal/mol	45.71	44.70	34.05	33.16	33.5 ± 0.5
ΔE (boat) in kcal/mol	55.60	54.76	41.96	41.32	44.7 ± 0.5

Table 12. Summary of activation energies for the Cope rearrangement via both transition states in kcal/mol

The activation energy calculation was done by calculating the difference in energies between the optimized reactant anti2 and the optimized chair and boat transition states. It is observed that chair conformation gives generally lower activation energy than the boat structure thus more favoured transition state. The structure optimized at B3LYP/6-31G* level of theory at 0K has closer activation energy to the experimental result. Thus B3LYP/6-31G* gives a better estimation of this transition structure than HF/3-21G.

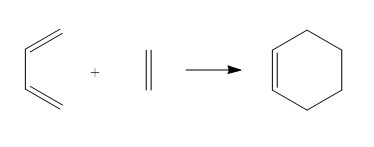
The Diels Alder Cycloaddition

In this exercise, AM1 semi-empirical method was used to compute the Diels Alder cycloaddition which is a concerted pericyclic reaction. The driving force of this reaction is the formation of a new σ bond between the π orbitals of the dieneophile and the diene which is stronger than the π bond. The reaction is not allowed without the HOMO-LUMO interation and a symmetry overlap.

Cis Butadiene

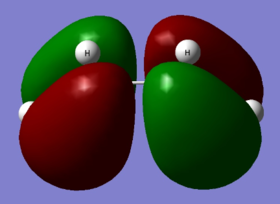
**Figure 13**. *The prototype reaction between butadiene and ethylene*

To study a prototype Diels Alder cycloaddition reaction between butadiene and ethylene, first a cis butadiene molecule was built using Gaussview and optimized using the AM1 semi-empirical molecular orbital method. The HOMO and LUMO of the butadiene were plotted. As seen the HOMO of cis-butadiene is anti-symmetric (a) and the LUMO is symmetric (s) with respect to plane.

The Transition State of prototype reaction between ethylene and butadiene

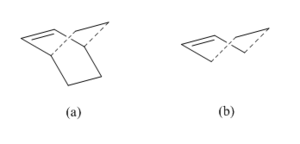
The Hessian method was used to estimate transition state for the reaction between ethylene and butadiene because these two reactants are relatively small and simple molecules. The transition state was drawn by first building a structure as (a) in Figure 16 then removing the -CH₂-CH₂- group to form the envelop structure as in (b). The clean option should not be used and the dashed bond length was guessed to be larger than 2.2 Å otherwise the geometry change would cause a failure in optimization.

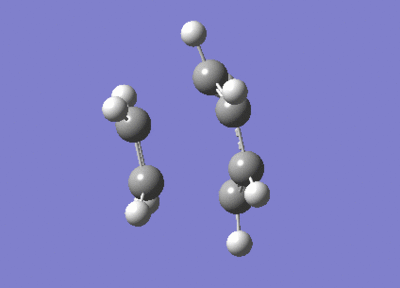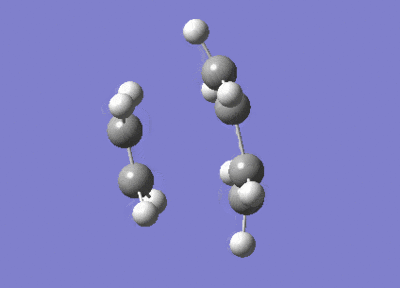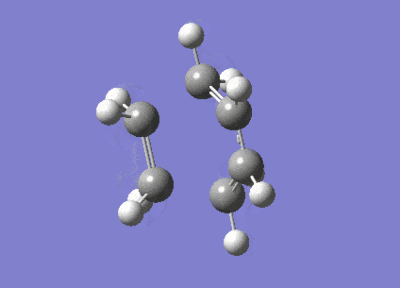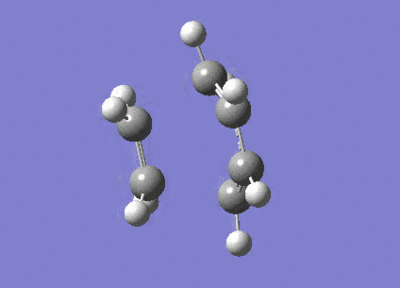
After the Hessian optimization, the transition structure has been successfully determined and an animation was generated in Figure 17. It has a C₁ symmetry point group and the bond lengths of two partly formed C-C bonds were measured to be 2.12Å. The typical sp³ and sp² C-C bond lengths are 1.54 Å and 1.47 Å respectively^[3]. The van der Waals radius of the C atom is 1.7 Å^[4]. The measured bond distance of the transition structure is larger than typical bond lengths but still within the van der Waals radius, suggesting the bond forming interation between the carbon atoms.

From the animation (Figure 17) the vibration directions of two molecules are opposite and they are approaching and leaving each other at the same time. This suggests the formation of the two bonds synchronous. The vibrational frequencies were also calculated and an infrared spectrum was simulated (Figure 20). An imaginary frequency of magnitude -955 cm^-1 was seen and the lowest positive frequency was observed at 147 cm^-1 which corresponded to the reactant vibration but not the bond formation.

The HOMO and LUMO molecular orbitals of this transition structure were visualized in Figure 18 and Figure 19. From these two figures it can be observed that the HOMO at the transition structure is anti-symmetric (a) while the LUMO is symmetric (s). Thus this anti-symmetric transition state HOMO is formed by the HOMO of cis-butadiene and the LUMO of ethylene with the knowledge that they are both anti-symmetrical. This conclusion agrees with the previous talked conditions for allowed reaction.

The cyclohexa-1,3-diene reaction with maleic anhydride

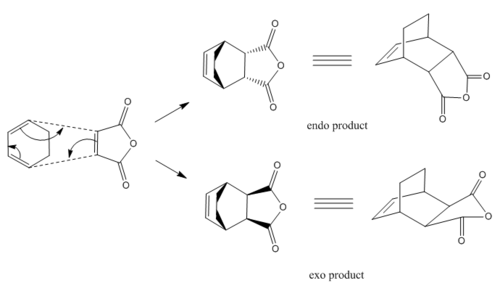
The exo and endo transition states were drawn according to Figure 21 with the new C-C bond formation line dashed and bond length estimation as 2.5 Å. Then the same Hessian method was applied to optimize the structures. The electronic energy of the endo structure was calculated to be -0.05150Ha and -0.05042Ha for the exo. This reaction is supposed to be kinetically controlled thus the lower energy endo transition state is more favoured.

The bond lengths of the partly formed C-C bond are 2.16 Å and 2.17 Å for endo and exo transition states respectively. Another measured C-C bond length is shown in Table 13 as 2.89 Å for endo (C3-C8 and C2-C7) and 2.95 Å for endo (C7-C10 and C8-C9). The longer atom distance indicates the larger steric repulsion in the exo transition state because of the extra existence of hydrogen atoms on C7 and C8.

Woodward and Hoffmann also proposed a secondary orbital overlap statement as an explanation of the endo stereo-preference in Diels Alder reactions^[5]. This secondary orbital overlap does not involve bond changes but π orbital interactions as the highlighted carbon atoms of the endo transition state in Table 13. Such overlap stablises the structure and lowers the energy of the endo transition state while there is no such effect existed in the exo transition state.


	endo	exo
Animation
Sum of electronic and zero-point Energies	0.133493	0.134880
Sum of electronic and thermal Energies	0.143683	0.144881
Sum of electronic and thermal Enthalpies	0.144627	0.145825
Sum of electronic and thermal Free Energies	0.097349	0.099117
Bond lengths
HOMO
Secondary orbital overlap effect
	File:XJB endo ts.log	File:XJB exo ts.log

Table 13. Summary of comparison of properties of endo and exo transition structures for reaction between cyclohexa-1,3-diene and maleic anhydride

Further work

The semiempirical/AM1 calculation is based on the "Neglect of Differential Diatomic Overlap (NDDO)" integral approximation, which neglects all two-electron integrals involving two-center charge distributions are neglected^[6]. The better optimization towards the endo and exo transition states should be done first by AM1 optimization followed by B3LYP/6-31G* reoptimization^[7]. The results are summarized in Table 14.


	endo	exo
Structure
Electronic energy/Hartrees	-612.68340	-612.67931
	File:XJB endo ts reopt.log	File:XJB exo ts reopt.log

Table 14. Reoptimization using B3LYP/6-31G* of endo and exo transition structures for reaction between cyclohexa-1,3-diene and maleic anhydride

Reference

↑ Nigerian Journal of Chemical Research, 2007, 12. DOI:10.4314/njcr.v12i1.
↑ The Journal of Chemical Physics., 2005, 122, pp 1-17. DOI:10.1063/1.1927521
↑ J. Phys. C: Solid State Phys., 1986, 19, pp 4613-4621.
↑ Z. Naturforsch., 2007, 62b, pp 235-243.
↑ J. Org. Chem., 1987, 52(8), pp 1469–1474. DOI:10.1021/jo00384a016
↑ http://www.cup.uni-muenchen.de/ch/compchem/energy/semi1.html
↑ J. Org. Chem., 2003, 68 (19), pp 7158–7166. DOI:10.1021/jo0348827

[soo-1] Nigerian Journal of Chemical Research, 2007, 12. DOI:10.4314/njcr.v12i1.

[IRC-2] The Journal of Chemical Physics., 2005, 122, pp 1-17. DOI:10.1063/1.1927521

[bondlength-3] J. Phys. C: Solid State Phys., 1986, 19, pp 4613-4621.

[bondlength2-4] Z. Naturforsch., 2007, 62b, pp 235-243.

[soot-5] J. Org. Chem., 1987, 52(8), pp 1469–1474. DOI:10.1021/jo00384a016

[6] ttp://www.cup.uni-muenchen.de/ch/compchem/energy/semi1.html

[7] J. Org. Chem., 2003, 68 (19), pp 7158–7166. DOI:10.1021/jo0348827

[1]

[2]

[3]

[4]

[5]

[6]

[7]