Rep:Mod:WorkshopMC11
Ammonia
Molecule Infromation
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP) in atomic units (au): -56.55776873
Point group: C3V
RMS gradient: 0.00000485 a.u.
Optimised N-H bond distance: 1.018 A
Optimised H-N-H bond angle: 105.741 degrees
Optimisation Table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986295D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Ammonia |
Link to completed NH3 optimisation
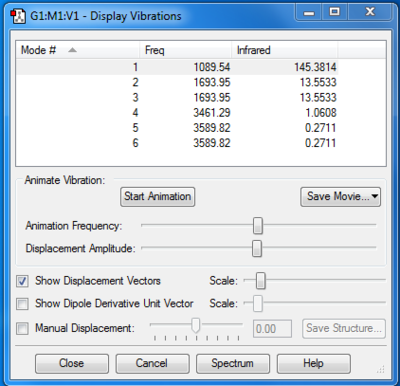
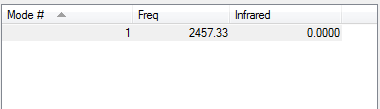
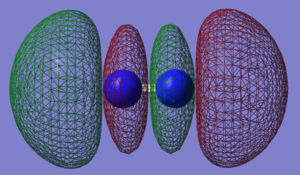
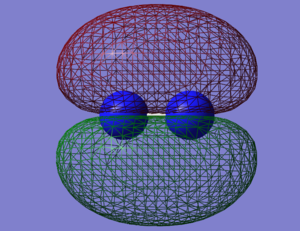
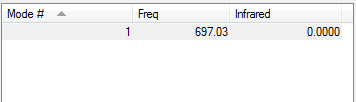
Molecule Vibrations
Modes expected from the 3N-6 rule: 6
Degenarate modes (ie have the same energy): 2-3 & 5-6
"Bending" vibrations and "bond stretch" vibrations: Bending = 1,2,3 Bond Stretch= 4,5,6
Highly symmetric mode: 4
"Umbrella" mode: 1
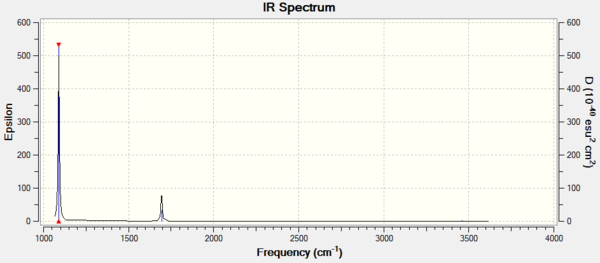
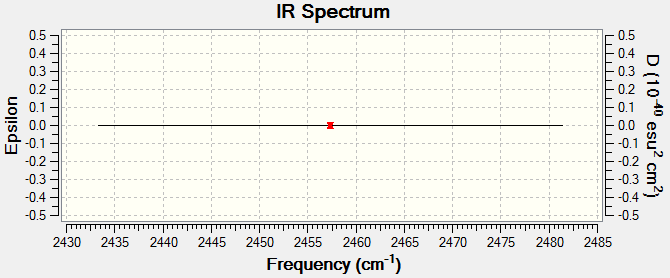
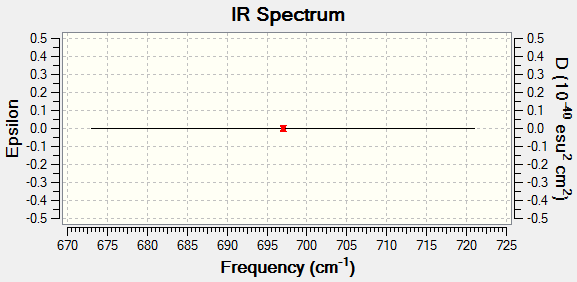
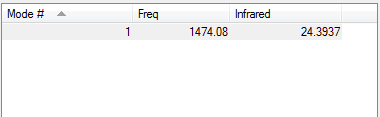
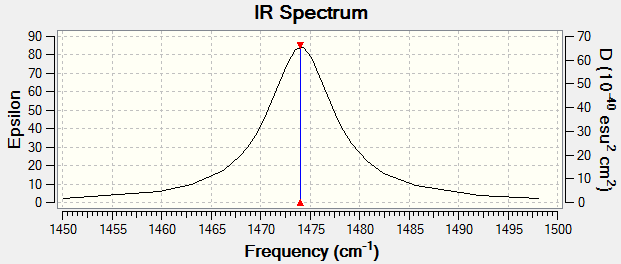
Number of bands expected in an experimental spectrum of gaseous ammonia: 2
Ammonia has 4 atoms therefore according to the equation 3N-6 N=4 and the number of modes expected are 6 as seen on the Display Vibrations. Bending Vibrations consist of the vibrations lower in energy, hence the 1st three whereas the last three are of higher energy and stretching vibrational modes. Number of bands that would be expected in a spectrum are 2 because there are 2 degenerate pairs of modes which would give 4 bands, as symmetric band that does not appear on the spectrum. Lastly a lower frequency mode that does not result to a band in the spectrum because the change in dipole is minor and dipole moment is proportional to band intensity. therefore the intensity of the band is too low and does not appear on the spectra. In conclusion two bands consisting of: 1 & 2/3.[1]
NH3 Charge Distribution
N-atom: -1.125
H-atoms: +0.357
Nitrogen has a much greater EN than the H hence it would be expected to have a negative charge due to its ability to attract electron density.
H2 Molecule
Molecule Infromation
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Point Group: D*H
Bond distance: 0.74 Å
H-H bond angle: 180 °
Optimisation Table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
H2 Molecule |
Link to completed H2 optimisation
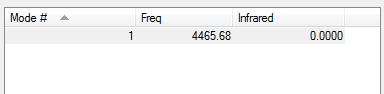
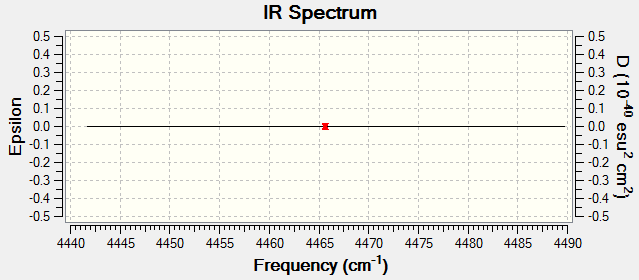
Molecule Vibrations
Charge distribution on H2
H2 is diatomic and both atoms have the same EN therefore there is no dipole moment and no charge on the molecule.
Nitrogen: N2
Molecule Information
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point Group: D*H
N-N bond distance: 1.11 Å
Optimisation Table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401143D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
N2 |
Link to completed N2 optimisation
Vibrational Modes
Charge Distribution
N2 is a diatomic molecule consisting of the same atoms which have the same EN hence no dipole and no charges.
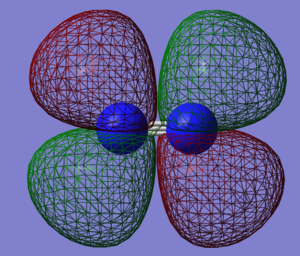
N2 Molecular Orbitals
Molecular Orbitals of nitrogen presented in order of increasing energy.
Reaction Energies
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.
Total Energy Change: -146.48 kJ/mol
The total energy for ammonia formation is negative therefore ammonia production is more energetically favorable as ammonia is more stable than its gaseous starting materials.[2]
Sulfur: S2
Molecule Information
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -796.32599779 a.u.
RMS gradient: 0.00000372 a.u.
Point Group: D*H
S-S bond distance: 1.93 Å
Optimisation Table
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000011 0.001800 YES
RMS Displacement 0.000016 0.001200 YES
Predicted change in Energy=-7.077700D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.9294 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
S2 |
Link to completed S2 optimisation
Vibrational Modes
Charge Distribution
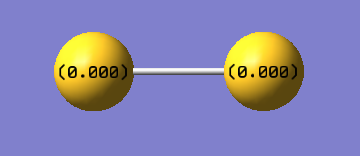
S2 is a diatomic molecule consisting of the same atoms which have the same EN hence no dipole and no charges.
S2 Molecular Orbitals
The molecular orbital energy-level diagram of S2:[3]
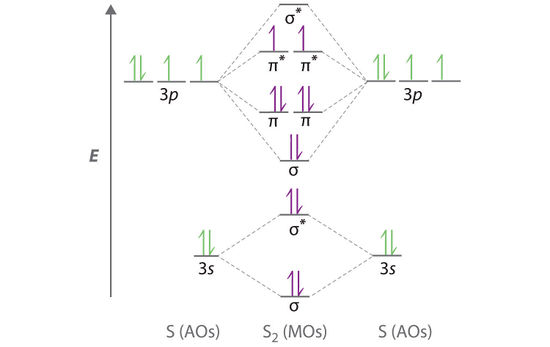
σ*u anti-bonding orbital
σg bonding orbital
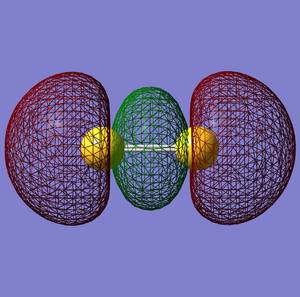
πu bonding orbital

π*g anti-bonding orbital

σ*u anti-bonding orbital

[4]
NO-
Molecule Information
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -129.81016799 a.u.
RMS gradient: 0.00000011 a.u.
Point Group: C*V
Dipole Moment:0.9230 Debye
NO- bond distance: 1.28 Å
Optimisation Table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.236925D-14
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.276 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
NO |
Link to completed NO- optimisation
Vibrational Modes
Charge Distribution
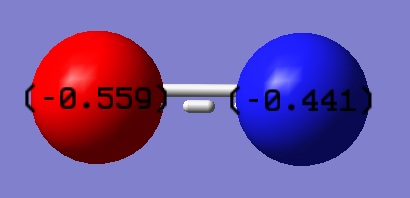
NO- is a molecule consisting of atoms with different EN and therefore has a dipole. O is more EN than N hence has a higher charge however as the difference in O & N EN is small the difference in the charges is small as well.
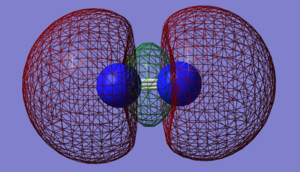
NO- Molecular Orbitals
The molecular orbital energy-level diagram of NO-[3]:
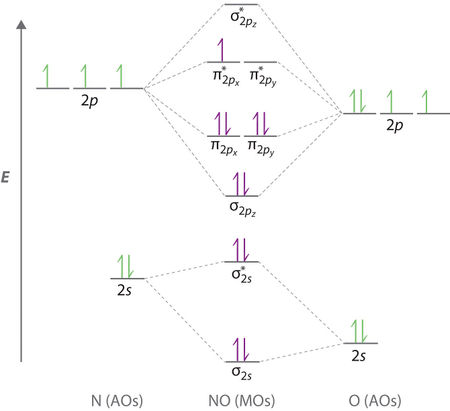
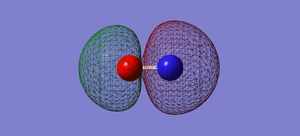
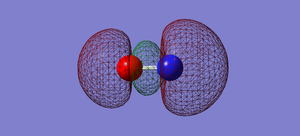
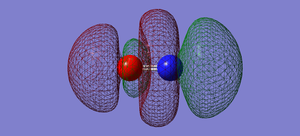
Molecular Orbitals are presented in order of increasing energy. The factor contributing to different sized MO's is the difference in EN between the atoms.
References
IR Spectroscopy[1] The Haber–Bosch process [2] Molecular Orbital Diagrams[3] Molecular Orbital Theory[4]
<references>
- ↑ 1.0 1.1 1.2 https://www2.chemistry.msu.edu/faculty/reusch/VirtTxtJml/Spectrpy/Infrared/infrared.htm
- ↑ 2.0 2.1 2.2 https://en.wikipedia.org/wiki/Haber_process
- ↑ 3.0 3.1 3.2 3.3 https://chemistry.stackexchange.com/questions/15315/nitric-oxide-dimerization
- ↑ 4.0 4.1 4.2 https://pubs.acs.org/doi/abs/10.1021/ed073pA136.1